一种求解多目标无约束0-1二次规划问题的文化基因算法

周莹，刘云霞

（深圳信息职业技术学院计算机学院，广东 深圳 518172）

【信息技术理论研究】

一种求解多目标无约束0-1二次规划问题的文化基因算法

周莹，刘云霞

（深圳信息职业技术学院计算机学院，广东 深圳 518172）

针对多目标无约束0-1二次规划问题，提出一种文化基因算法。该算法采用基于分解的多目标演化算法框架，能够获得分布均匀的非占优解；同时，采用一种简单、有效的禁忌搜索，能够利用更多问题相关的信息，获得质量更优的非占优解。该算法在优化的过程中能够动态地平衡多样性与收敛性。实验结果证明该算法能够很好地求解多目标无约束0-1二次规划问题，并且性能优于目前求解该问题较先进的算法。

多目标无约束0-1二次规划问题；文化基因算法；基于分解的多目标演化算法；禁忌搜索算法

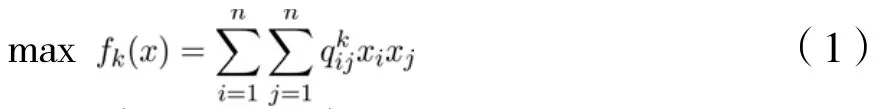
mUBQP具有广阔的应用场景[1]。在实际生活中，大量难以解决的问题都可转化为mUBQP。此外，许多图论问题也可转化为mUBQP，如双目标着色问题[1]。mUBQP是一种多目标优化问题，该类问题通常不存在一个能使多个目标同时达到最优的解，而是存在一组可供选择的折中解。因此，需设计多目标优化算法对其进行求解。

mUBQP是一种新的多目标优化问题，据我们所知，目前对mUBQP的研究成果仍然较少。2013年，文献[1]首先提出一组mUBQP的测试数据集。该测试数据集按照问题规模、密度、目标个数以及目标之间的相关性分为50个算例。其次，作者借鉴成功求解单目标UBQP的算法，提出第一个求解mUBQP的算法：混合型元启发式算法（HM）。该算法结合基于Pareto支配关系的进化算法与禁忌搜索来获得一组Pareto最优解。然而，HM并不能很好地求解大规模的算例。随后，Zhou等[2]提出一种边界解引导的多目标优化算法（DTS），用于求解mUBQP。该算法优先优化边界方向上的解。当无法继续优化边界解时，算法逐渐改变优化的方向，以填补边界解之间的间隙。实验结果显示DTS的性能优于HM。然而，该算法对mUBQP的求解效果并不能令人满意。

为了能够更好地求解mUBQP，本文提出一种文化基因算法（memetic algorithm，MA）。MA采用基于分解的多目标演化算法框架（MOEA/D），能够获得分布均匀的非占优解。此外，MA采用一种简单、有效的禁忌搜索（TS），能够利用问题相关的信息进行求解，因此能够获得质量更好的解。为了验证算法的有效性，本文将MA用于求解50个mUBQP的算例，并将其与目前求解该问题较为先进的算法：DTS进行对比。实验结果显示MA显著地优于DTS。

1 求解mUBQP的文化基因算法

MA采用MOEA/D[3]的算法框架，将mUBQP分解为个子问题，每一个子问题关联一个个体，并且关联一个权重向量。然后，利用进化算法与局部搜索算法同时优化这些子问题。在优化的过程中，MA采用交叉操作生成新的子代个体，并且采用一种简单的TS来提升解的质量。MA的优化过程如图1所示。

图1 MA的优化过程Fig.1 The image of optimization procedure in MA

MA的特点如下：

1）采用MOEA/D的算法框架，可以通过分布均匀的权重向量生成分布较为均匀的非占优解，从而保持良好的多样性；

2）TS能够很好地利用问题相关的信息来有效地提升解的质量，从而使算法保持良好的收敛性。

1.1 MA的算法流程

MA使用一组分布均匀的权重向量，采用加权法将问题分解为一系列子问题。设某个子问题所关联的权重向量为，该问题的目标函数可描述如下：

交叉操作（步骤10）：用于生成新的后代个体；优化操作（步骤11）：采用TS提升解的质量；存档更新操作（步骤12）：用于更新外部存档。

接下来将分别介绍这三种操作。

1.2 交叉操作

MA采用均匀交叉操作（uniform crossover）[1]生成新的后代个体。首先，算法从每个子问题的邻域中随机选出两个父代个体、；然后，与中共同的决策变量直接由子代个体继承，其余的决策变量将以随机的方式赋予子代个体。该操作可由算法2来描述，其中表示随机选取0或1。

1.3 优化操作

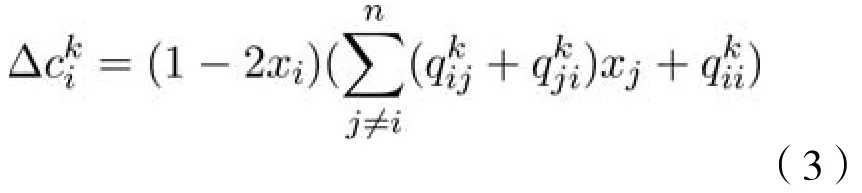
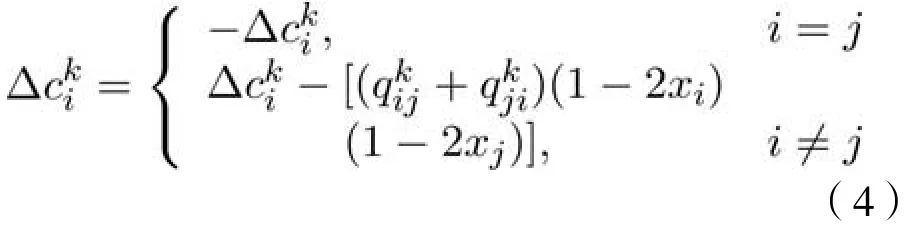
TS直接对每个子问题进行优化。因此，TS使用式2来评估每个子问题关联的解的质量。TS采用禁忌表(tabu list)来避免迂回搜索，并选择邻域中最好的解（best improvement strategy）作为可接受的候选解。翻转决策变量之后，该变量进入禁忌表中，并且在之后代内不得再次被翻转（禁忌准则），除非能够获得优于当前最优的解（赦免准则）。在TS中，用参数控制搜索深度，即经过次邻域操作之后算法停止，最后返回搜索过程中找到的最优解。

1.4 存档更新操作

1.5 初始化与停止条件

MA以停止时间为停止条件。为了公平对比算法之间的性能，所有算法的停止时间都设为一致。

2 实验及结果分析

本节通过一系列实验来验证MA的性能。本节采用的测试算例为50个mUBQP算例，可通过网站（http://mocobench.sourceforge.net/index.php?n=）下载。实验的运行环境描述如下：

1）处理器：Pentium＠ Dual-Core CPU E5400 @ 2.70GHZ

2）内存：4.00GB

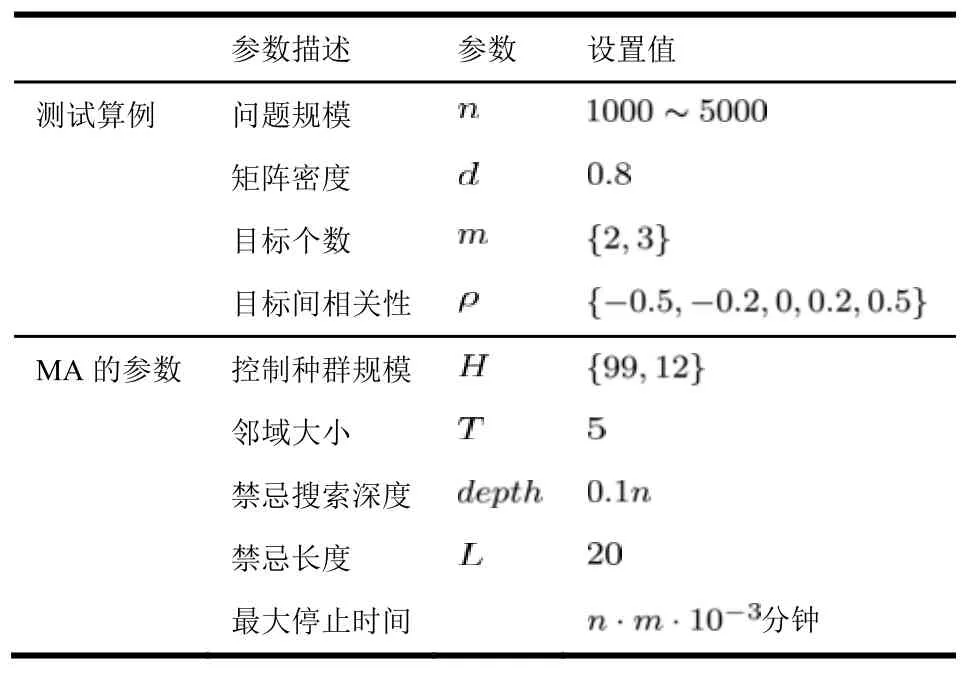
表1 测试算例与MA中参数设置Tab.1 Parameter setting for instances MA

由于DTS[2]是目前为止求解mUBQP较为先进的算法，因此将DTS作为MA的对比算法。所有算法均用C语言实现。DTS中所有参数的设置均与文献[2]相同。测试算例的描述与MA中的参数设置见表1。其中，种群规模由参数控制。权重向量的每个分量的取值为集合：

为了公平地进行对比，两种算法均在相同的运行环境下运行。每个算法对每个算例单独运行20次。接下来，本节给出算法的性能指标，并给出MA与DTS的算法对比。

2.1 性能指标

多目标优化算法的性能从两方面评价，分别为多样性与收敛性。由于单一的性能指标无法同时反映这两个评价标准[5]，因此本节分别采用以下两种性能指标来评价多目标算法的性能：

1）获得的非占优解集与参考集之间的度量（inverted generational distance，IGD）[3]：该指标由Zhang和Li提出，定义如下：

2）超体积度量（hypervolume，HV）[6]：该指标由Zitzler等提出，用于度量至少被非占优解集中的一个解占优的目标空间的体积。HV同样能够度量算法的多样性和收敛性。

HV（IGD）的值越大（越小），说明得到的非占优解越接近真实的PF，因此算法的多样性与收敛性越优。由于无法获取mUBQP真实的PF，因此对于每个算例，将所有算法在该算例上获得的非占优解作为该算例的参考集。此外，由于不同目标的取值范围不同，所有解的目标值均做归一化处理。

2.2 MA与DTS 的对比

表2-3显示了两种算法对每个算例独立运行20次，在IGD与HV上得到的平均值。为了进一步显示算法之间的差异，我们采用Wilcoxon测试[7]（显著水平为0.05）对算法进行统计测试。表中粗体的数字代表对应的算法在算例上得到的结果显著地优于对比算法。从表2-3中可以看出，MA对35个算例在IGD与HV上得到的结果均显著地优于DTS，尤其对于IGD指标，MA对所有50个算例得到的结果均显著地优于DTS。此外，随着目标数与问题规模的增长，DTS的求解能力逐渐下降。因此，从实验结果可以看出，MA将MOEA/D与TS结合，能够很好地平衡多样性和收敛性，并且能够获得更优的非占优解。

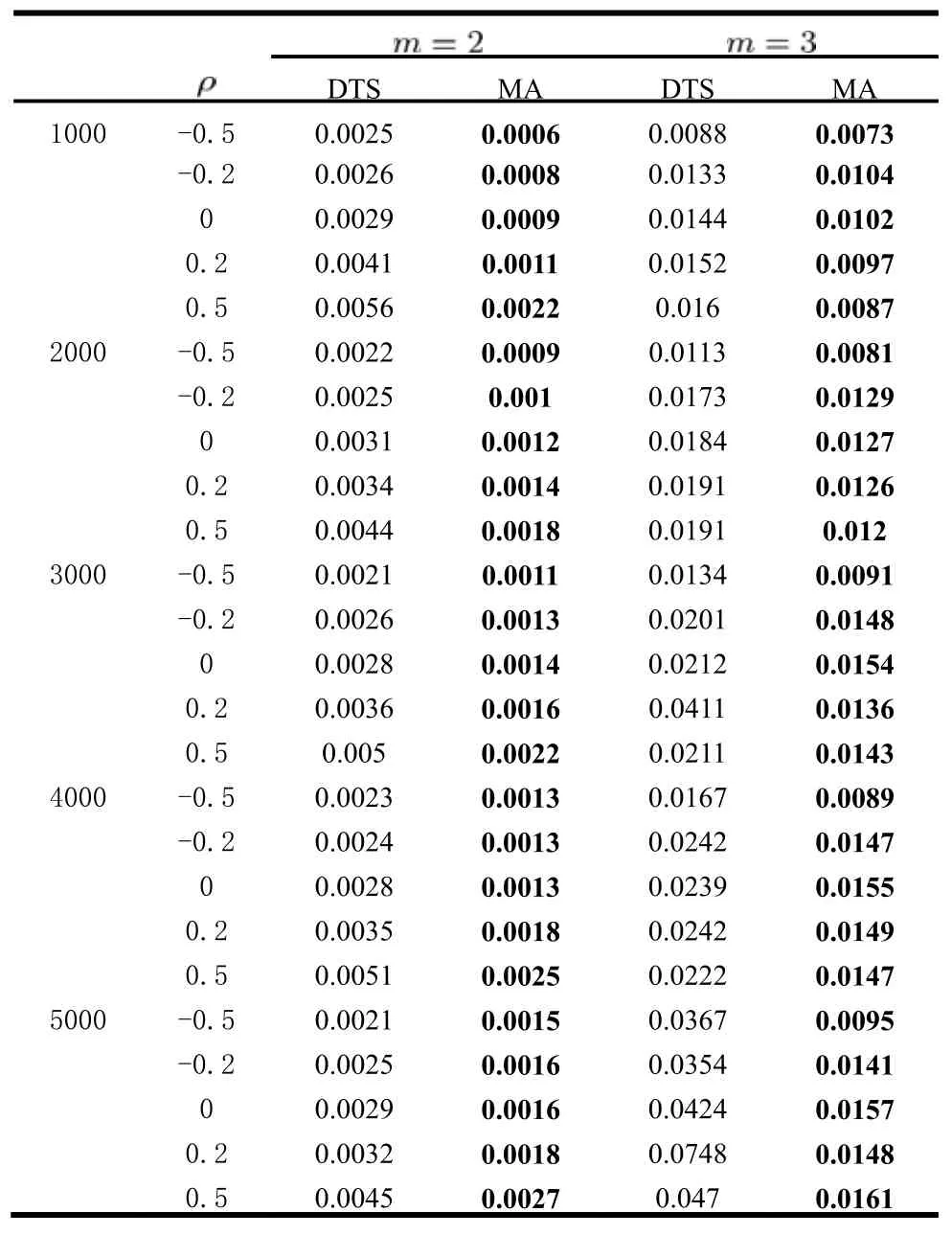
表2 DTS与MA在IGD上的平均值Tab.2 Average values in terms of IGD for DTS and MA

为了更好地显示两种算法的性能，图2-3显示了MA与DTS对，的四组算例，独立运行20次中得到IGD最好的非占优解。从图中可以看出，MA不论在解的分布还是非占优解的数量上均优于DTS。因此，从图的角度进一步反映了MA具有良好的多样性与收敛性，是一种有效求解mUBQP的方法，并且性能显著地优于DTS。

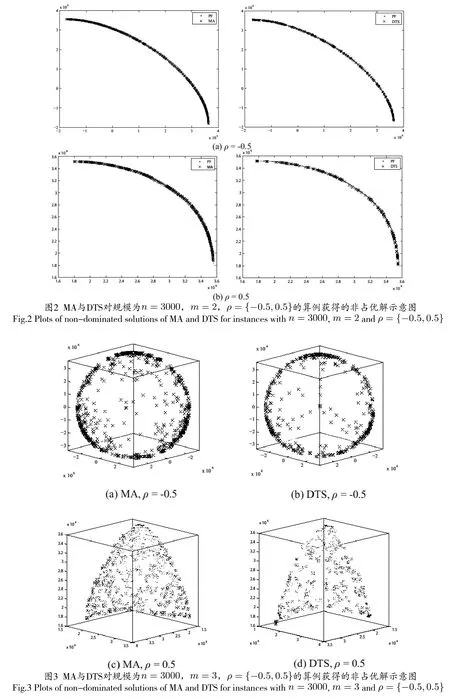
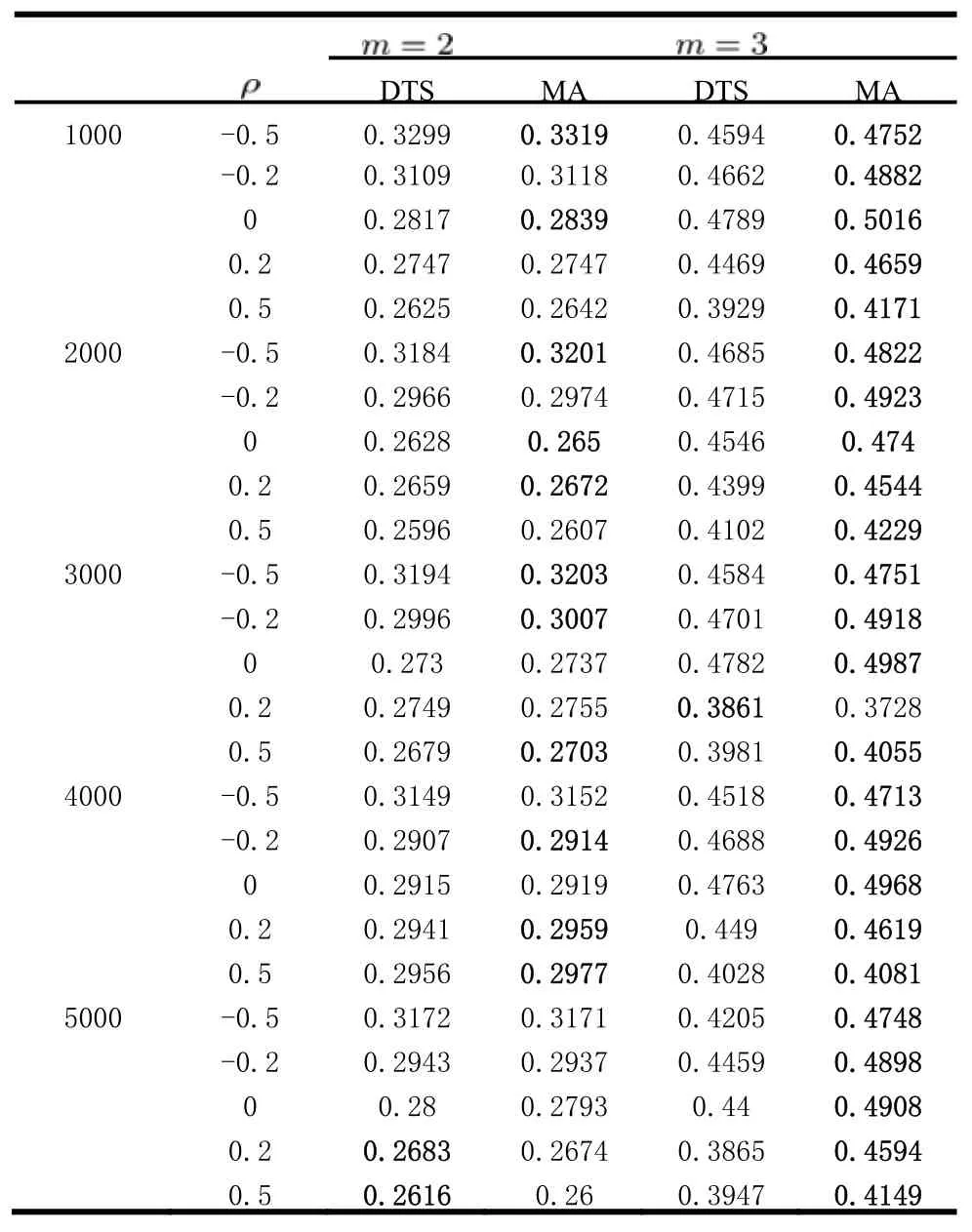
表3 DTS与MA在HV上的平均值Tab.3 Average values in terms of HV for DTS and MA

3 结论

本文提出一种用于求解mUBQP的文化基因算法（MA）。MA采用基于分解的演化算法框架（MOEA/D），将问题分为若干个子问题，并通过分布均匀的权重向量保持算法的多样性。此外，MA采用禁忌搜索（TS）进一步提升解的质量。该TS具有简单、有效的特点，能够较好地利用问题相关的信息，从而使整个算法具有良好的收敛性。实验结果表明，MA不仅能够有效地求解mUBQP，而且性能优于目前求解MA较为先进的算法。

今后的工作可以从以下几个方面展开：首先，本文提出的算法为通用性算法，可以用于求解其他0-1组合优化问题；其次，可以采用有界存档，如基于支配关系[8]的存档，储存搜索过程中找到的非占优解，从而进一步提升算法的效率；最后，可采用自适应的参数，在搜索过程中动态地调整参数大小，以获得更好的结果。

References)

[1]Liefooghe A,Verel S,Hao J K.A hybrid metaheuristics for multiobjective unconstrained binary quadratic programming[J].Applied Soft Computing,2014,16:10-19.

[2]Zhou Y,Wang J,Yin J.A Directional-biased Tabu Search Algorithm for Multi-objective Unconstrained Binary Quadratic Programming Problem[C].//Proc Six International Conference on Advanced Computational Intelligence (ICACI),Washington,DC,USA:IEEE,2013,pp.281-286.

[3]Zhang Q,Li H.MOEA/D:A multiobjective evolutionary algorithm based on decomposition[J].Evolutionary Computation,IEEE Transactions on,2007,11(6):712-731.

[4]Wang J,Zhou Y,Yin J.Combining tabu Hopfield network and estimation of distribution for unconstrained binary quadratic programming problem[J].Expert Systems with Applications,2011,38(12):14870-14881.

[5]Zitzler E,Thiele L,Laumanns M,et al.Performance assessment of multiobjective optimizers:An analysis and review[J].IEEE Transactions on Evolutionary Computation,2003,7(2):117-132.

[6]Zitzler E,Laumanns M,Thiele L.SPEA2:Improving the strength Pareto evolutionary algorithm[M].//Evolutionary Methods for Design,Optimization and Control with Applications to Industrial Problems.Berlin:Springer,2002:95-100.

[7]Derrac J,García S,Molina D,et al.A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms[J].Swarm and Evolutionary Computation,2011,1(1):3-18.

[8]Laumanns M,Thiele L,Deb K,et al.Combining convergence and diversity in evolutionary multiobjective optimization[J].Evolutionary Computation,2002,10(3):263-2.

A memetic algorithm for multiobjective unconstrained binary quadratic programming

ZHOU Ying ,LIU Yunxia
（School of Computer Science,Shenzhen Institute of Information Technology,Shenzhen 518172,P.R.China）

This paper proposes a memetic algorithm (MA) for multiobjective unconstrained binary quadratic programming problem.In MA,multiobjective evolutionary algorithm based on decomposition (MOEA/D) framework is adopted to obtain well-distributed nondominated solutions.At the same time,More problem-specific knowledge can be extracted by using a simple and effective tabu search (TS)，and high-quality solutions can be generated.Therefore,MA can balance the diversity and convergence well during the whole optimization process.Experimental results show that MA outperforms the previous state-of-the-art algorithm for mUBQP cases.

multiobjective unconstrained binary quadratic programming;memetic algorithm;multiobjective evolutionary algorithm based on decomposition;tabu search

TP312

：A

1672-6332（2014）03-0001-07

【责任编辑：高潮】

2014-09-01

广东省自然科学基金项目（项目编号：S2012010008964）；深圳市科技计划项目（项目编号：JCYJ20120615103057639）

周莹（1987-），女（汉），陕西富平人，博士。主要研究方向：计算智能与数据挖掘。E-mail:dyingdy@gmail.com