介质光学厚度对光子晶体透射谱特性的调制

潘继环，苏 安，蒙成举

(河池学院物理与机电工程学院，广西宜州 546300)

介质光学厚度对光子晶体透射谱特性的调制

潘继环，苏 安，蒙成举

(河池学院物理与机电工程学院，广西宜州 546300)

利用传输矩阵法理论，研究介质光学厚度对一维光子晶体(AB)5(BA)5透射谱特性的影响，结果表明:只要A、B介质光学厚度满足DA=DB，随着介质光学厚度的增大，光子晶体透射峰的透射率、频率位置和带宽均保持不变;当A、B介质的光学厚度不相等即DA≠DB时，随着DA或DB，或DA、DB的增大，禁带中透射峰的透射率不变但带宽变宽，且当DA＞DB时透射峰向高频方向移动，反之则向低频方向移动。介质光学厚度对光子晶体透射谱的调制规律，可为光子晶体模型的构建、窄带光学滤波器和光学开关的设计等提供有益参考。

光子晶体;光学厚度;调制;透射谱

1 引 言

光子晶体［1－2］是一种不同介电常数介质周期性排列的人工薄膜结构光学材料，自从其概念诞生以来，人们对它进行了广泛而深入的研究，并取得了大量的研究成果。由于光子晶体存在可以剪裁光子的带隙结构，所以研究者们预测，光子晶体将掀起新一轮通信材料的革命，而且最值得的关注的是用光子替代电子进行信息的传输，学者们认为能够完成这个任务的正是光子晶体这个材料载体。因此，光子晶体从20世纪80年代末到现在，一直是一个热门的研究课题［3－8］。

光学厚度作为衡量光子晶体薄膜介质的长度指标之一，其大小变化对光子晶体的空间结构和透射谱的特性一定会产生影响。以往的文献一般只从单一的介质光学厚度对透射谱特性影响进行研究，而光子晶体普通由两种或两种以上基元薄膜介质周期性排列而成，所以各薄膜介质基元光学厚度之间的关联性，与光子晶体的透射谱特性也一定存在某种关系，并且，基元薄膜介质光学厚度之间的关联性对对透射谱的影响研究，目前还未见报道［9－11］。基于这种考虑，本文构造对称结构一维光子晶体(AB)5(BA)5模型，研究A、B介质光学厚度DA、DB的关联性对光子晶体透射谱的影响规律，为光子晶体的理论研究、光学器件的设计，或者光子晶体模型的构建和制备等提供理论依据。

2 研究方法与模型

研究方法采用理论比较成熟且计算比较直观的传输矩阵法［3－8，12］。当光在周期性排列的分层介质中传播时，可分别用一传输矩阵来描述光在各层介质中的行为，光在介质周期性排列整体中的传输行为可用一总传输矩阵描述，而且总传输矩阵等于各分层介质矩阵之积，通过总传输矩阵即可计算出光在光子晶体中传输的电场分布、透射率和反射率等。传输矩阵的详细介绍可见文献［12］，在此不再重述。

研究模型为(AB)5(BA)5，各介质层及其参数分别为:A为硫化锌(ZnS)，nA=2.35，dA=740 nm，B为氟化镁(MgF2)，nB=1.38，dB=1260 nm。根据光子晶体结构参数和光学厚度［9－11］计算公式Di= nidi(i为A或B介质)可知，nAdA=nBdB=D0= 1739 nm，即介质层A、B的光学厚度相等。考虑光垂直入射，利用传输矩阵法理论和Mathlab编程计算，可模拟绘制出光子晶体(AB)4(BA)4、(AB)5(BA)5和(AB)6(BA)6透射谱，如图1(a)、(b)、(c)所示，图中ω/ω0是归一化频率单位。从图1可见，在光子晶体很宽的主禁带中心1.0ω/ω0频率处出现了1条透射率为100%的透射峰，透射谱具有对称结构光子晶体的透射特征［7－8］，而且随着光子晶体排列周期数的增大，透射峰数目和透射率保持不变，但透射峰的带宽会变窄。光子晶体的这种透射谱特性，可实现窄带光学滤波功能。

3 介质光学厚度对透射谱特性的调制

3.1 DA=DB时光子晶体的透射谱

首先，保持光子晶体(AB)5(BA)5的其他参数不变，以A、B介质的初始光学厚度D0为基数，使它们以任意数和倍数增大，即DA=DB=D0、D0+ 20 nm、D0+40 nm，或DA=DB=D0、2.0D0、3.0D0时，计算模拟得光子晶体(AB)5(BA)5的透射谱，如图2(a)～(f)所示。

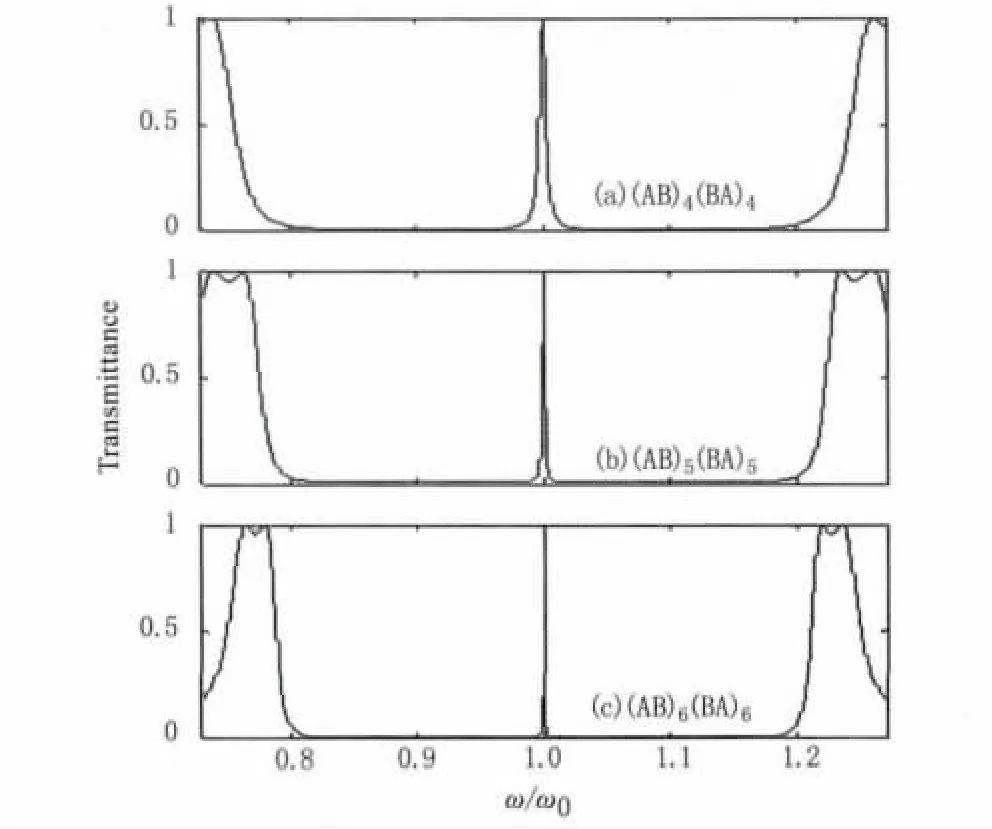
图1 周期数对光子晶体透射谱的影响Fig.1 Transmission spectrum of photonic crystals versus cycle

图2 DA=DB时光子晶体的透射谱Fig.2 Transmission spectrum of photonic crystals of DA=DB

从图2可见，无论A、B介质光学厚度按任意数还是整数倍增大，光子晶体(AB)5(BA)5的禁带中始终只有1条透射率为100%的透射峰，而且此单透射峰位置保持在禁带中心1.0ω/ω0频率处，同时透射峰的带宽保持恒定，如DA=DB=D0、D0+40、2.0D0、3.0D0时，透射峰的带宽均为 BW = 0.0019 nm。光子晶体透射峰的带宽(bandwidth-BW)一般以透射峰的半高全宽(FWHM)［5－6］表示。

可见，无论光学厚度按任意数还是倍数增大，只要A、B介质的光学厚度相等，则光子晶体透射峰的带宽、透射率及所处频率位置等均不变，即保持DA=DB条件下，A、B介质光学厚度DA、DB大小变化对光子晶体透射峰特性不产生影响。

3.2 DA≠DB时光子晶体的透射谱

仍然保持光子晶体(AB)5(BA)5的其他参数不变，以A、B介质的初始光学厚度D0为基数，在A、B介质光学厚度不相等的条件下使它们增大，即取DA=D0、D0+400 nm、D0+800 nm，DB=D0、D0+ 20 nm、D0+40 nm，或DA=D0、D0+20 nm、D0+ 40 nm，DB=D0、D0+400 nm、D0+800 nm时，计算模拟得光子晶体(AB)5(BA)5的透射谱如图3(a)～(f)所示。

图3 DA≠DB时光子晶体的透射谱Fig.3 Transmission spectrum of photonic crystals of DA≠DB

由图3可见，保持A介质光学厚度大于B介质光学厚度的条件下(DA＞DB)，随着DA、DB的增大，光子晶体(AB)5(BA)5主禁带中的透射峰向高频方向移动，而且透射峰的带宽变宽，但透射峰的透射率保持100%不变。当DA=D0、D0+400 nm、D0+800 nm时，光子晶体透射峰所在频率位置分别为1.0ω/ω0、1.025ω/ω0、1.044ω/ω0，带宽分别为 0.0019 nm、0.0021 nm、0.0028 nm，分别如图3(a)～(c)所示。当DA＜DB时，随着DA、DB的增大，光子晶体(AB)5(BA)5主禁带中的透射峰却向低频方向移动，而且透射峰的带宽也变宽，同时透射峰的透射率仍然保持100%不变。当DB=D0、D0+400 nm、D0+800 nm时，光子晶体透射峰所在频率位置分别为1.0ω/ω0、0.9763ω/ω0、0.9570ω/ω0，带宽分别为 0.0019 nm、0.0020 nm、0.0024 nm，分别如图3(d)～(f)所示。

可见，当A、B介质的光学厚度不相等时，增加介质A、B的光学厚度，除透射峰的透射率保持100%不变外，透射峰的所处的频率位置和带宽均发生了改变。

进一步地，分别在A、B介质光学厚度相等和不相等的情况下，计算A、B介质光学厚度对透射峰位置的影响规律，如图4所示。图中带圆圈实线是A、B介质光学厚度相等时透射峰频率位置对光学厚度变化的影响曲线，带方格虚线是保持 DB不变且DA＞DB时透射峰频率位置对光学厚度变化的影响曲线，带三角间断线是保持DA不变且DA＜DB时透射峰频率位置对光学厚度变化的影响曲线。

图4 介质光学厚度对光子晶体透射谱的影响曲线Fig.4 Transmission spectrum of photonic crystals versus optical thickness

结合图3和图4进一步说明，只要A、B介质的光学厚度保持相等DA=DB，无论怎样增加两介质的光学厚度，光子晶体透射峰所处的频率位置均保持在禁带中心1.0ω/ω0处;只要保持DA＞DB，无论DA、DB单独增大还是同时增大，光子晶体透射峰均向高频方向移动;反之，只要保持DA＜DB，无论DA、DB单独增大还是同时增大，光子晶体透射峰则均向低频方向移动。计算还发现，DA=DB时，无论怎样增大DA、DB，透射峰的带宽保持不变，而DA＞DB或DA＜DB时，无论怎样增大DA、DB，光子晶体透射峰的带宽都不断加宽，以致于当DA、DB增大到一定数值后，透射峰变宽趋向于透射带。

可见，在保持A、B介质光学厚度相等情况下，A、B的光学厚度大小对光子晶体的透射特性不产生影响，这个特性对光子晶体构造时薄膜介质厚度的选定或制备具有重要意义。当A、B介质光学厚度不相等时，介质光学厚度对透射峰的频率位置和带宽将产生影响，这个特性对光子晶体实现可调性光学滤波器、光学开关功能等具有参考意义。

4 结论

利用传输矩阵法理论研究介质光学厚度对一维光子晶体(AB)5(BA)5透射谱的影响规律，得出如下结论:

(1)A、B介质光学厚度DA=DB情况下，DA、DB变化对光子晶体透射峰的频率位置、透射率和带宽不产生影响。

(2)A、B介质光学厚度DA≠DB情况下，A、B介质的光学厚度变化对光子晶体透射峰的透射率无影响，但对透射峰的带宽和频率位置有调节功能，而且DA＞DB与DA＜DB情况不同。DA＞DB时，随着DA或DB，或DA、DB增大，相反当DA＜DB时，随着DA或DB，或DA、DB增大，透射峰则向低频方向移动，同时随着DA或DB，或DA、DB增大，透射峰的带宽变宽。

介质光学厚度对光子晶体透射峰的透射率、频率位置和带宽等特性的调制规律，对光子晶体设计可调性光学滤波器、光学开关、光子晶体结构模型和理论研究等均具有参考作用。

［1］Yablonovitch E.Inhibited spontaneous emission in solidstate physics and electronics［J］.Phys Rev Lett，1987，58 (20):2059－2061.

［2］John S.Strong localization of photons in certain disordered dielectric superlattices［J］.Phys Rev Lett，1987，58(23): 2486－2489.

［3］SU An，GAOYingjun.Light propagation characteristics of one-dimensional photonic crystal with double-barrier quantum well［J］.Acta Physica Sinica，2012，61(23): 234208.(in Chinese)

苏安，高英俊.双重势垒一维光子晶体量子阱的光传输特性研［J］.物理学报，2012，61(23):234208.

［4］MENG Chenju，SU An.Absorption’s influence on the transmission spectrum ofmirror symmetry one-dimension photonic crystal［J］.Laser＆Infrared，2011，41(11):1248－1252.(in Chinese)

蒙成举，苏安.吸收对镜像对称一维光子晶体透射谱的影响［J］.激光与红外，2011，41(11):1248－1252.

［5］SU An，MENGChengju，GAO Yingjun.Filter with one-dimensional photonic crystal quantum well possessing highquality filtering functions［J］.Chinese J.Lasers，2013，40 (10):1006001.(in Chinese)

苏安，蒙成举，高英俊.实现高品质滤波功能的一维光子晶体量子阱滤波器［J］.中国激光，2013，40 (10):1006001.

［6］SU An，MENGChengju，GAO Yingjun.Effect of structure period number on the transmission quality of photonic quantum well［J］.Laser＆ Optoelectronics Progress，2013，50(01):0123021.(in Chinese)

苏安，蒙成举，高英俊.结构周期数对光量子阱透射品质的影响研究［J］.激光与光电子学进展，2013，50 (01):0123021.

［7］SU An，QINZongding，GAO Yingjun.Transmission properties of one-dimension photonic crystal quantum well with mirror symmetry structure［J］.Laser＆Infrared，2011，41 (8):0889－0893.(in Chinese)

苏安，覃宗定，高英俊.镜像对称结构一维光量子阱的光传输特性［J］.激光与红外，2011，41(8): 0889－0993.

［8］SU An.Photonic crystal quantum well with function of multi-channel photonic filtering and amplifying［J］.Infrared and Laser Engineering，2013，42(3):727－732.(in Chinese)

苏安.实现多通道光滤波与放大功能的光子晶体量子阱［J］.红外与激光工程，2013，42(3):727－732.

［9］LIU Qineng.Analytical study on total reflection tunnel effect of 1-D photonic crystal［J］.Acta Optica Sinica，2012，32(2):0219002.(in Chinese)

刘启能.一维光子晶体的全反射隧穿效应的解析研究［J］.光学学报，2012，32(2):0219002.

［10］CHEN Haibo，GAO Yingjun，HAN Junting.Effect of optical thickness on characteristics of photonic forbidden band of 1D three element photonic crystal［J］.Acta Photonica Sinica，2008，37(11):2210－2212.(in Chinese)

陈海波，高英俊，韩军婷.光学厚度对一维三元光子晶体禁带特性的影响［J］.光子学报，2008，37(11): 2210－2212.

［11］GENG Jiguo，ZHENG Jiakui.Study of optical transmission spectra of one-dimensional photonic crystalswhich optical width isn’tλ0/4［J］.Journal of Shandong Normal University:Natural Science，2007，22(3):59－61.(in Chinese)

耿继国，郑家奎.介质层光学厚度为非λ0/4的一维光子晶体透射谱研究［J］.山东师范大学学报:自然科学版，2007，22(3):59－61.

［12］WANG Hui，LIYongping.An eigen matrixmethod for obtaining the band structure of photonic crystals［J］.Acta Physica Sinica，2001，50(11):2172－2178.(in Chinese)

王辉，李永平.用特征矩阵法计算光子晶体的带隙结构［J］.物理学报，2001，50(11):2172－2178.

M odulation of optical thickness on transm ission spectrum of photonic crystal

PAN Ji-huan，SU An，MENG Cheng-ju
(School of Physics and Mechanical＆Electronic Engineering，Hechi University，Yizhou 546300，China)

Themodulation of optical thickness on transmission spectrum of one-dimensional photonic crystalwas studied by using transfermatrix theory.The results show that the transmittance，frequency and bandwidth of transmission peak are not changed with increasing the optical thickness ofmedium when the optical thickness of A and B medium are equivalent(DA=DB);when the optical thickness DAand DBare not equivalent(DA≠DB)，with increasing DAor DBor DAand DB，the transmittance of transmission peak is not changed，but the bandwidth is widen，and when DA＞DB，the transmission peak shifts to higher frequency，on the contrary，the transmission peak shifts to the lower frequency.These laws ofmodulation can provide a useful reference for construction of the photon crystalmodel and design of narrow band optical filter and optical switch.

photon crystal;optical thickness;modulation;transmission spectrum

O431

A

10.3969/j.issn.1001-5078.2014.05.017

1001-5078(2014)05-0559-04

广西自然科学基金项目(No.2011GXNSFA018145);广西高校科学技术研究重点项目(No.2013ZD058，2013YB206);河池学院重点科研基金资助课题(No.2013ZA－N003，2013B－N005)资助。

潘继环(1972－)，男，副教授，主要从事光子晶体方面的研究。E-mail:panjihuan@163.com

2013-09-12;

2013-10-10