采动覆岩承载结构与渗透特性演化分析

赵维国，王世超，王维华，李宏艳

(1.黑龙江龙煤集团双鸭山分公司，黑龙江双鸭山155100;2.煤炭科学研究总院，北京100013;3.煤炭科学研究总院矿山安全技术研究分院，北京100013;4.煤炭资源高效开采与洁净利用国家重点实验室 (煤炭科学研究总院)，北京100013)

瓦斯作为一种伴生清洁能源具有很高的利用价值［1］，研究采动影响下上覆岩层渗透特性的演化规律，对于指导工程实践中瓦斯抽采具有重要作用。由于煤岩的层状结构，以及各层物理力学性质的差异，在采动影响下各层间产生离层，部分区域应力集中，导致煤岩体达到承载极限，发生破断产生裂隙，进而影响覆岩的渗透特性。采动引起的岩层移动包含了变形、离层、破断、冒落等复杂力学行为，并且是个动态过程，因此，表征煤岩体渗透特性的渗透率和应力的关系不再满足于简单的弹性状态下的函数关系［2］。因此，建立基于应力演化与覆岩渗透率之间的函数关系，是研究采动覆岩渗透特性演化规律的关键所在。采动应力场的演化过程，影响因素较多，物理过程复杂，现场监测受到制约，所以采用数值试验是行之有效的方法。在采动覆岩的渗流演化规律方面，国内外学者进行了大量研究，文献［3］至文献 ［7］利用不同数值模拟的方法已经得到了一些非常有价值的成果。

本文以王坡矿为工程背景突破局限于个体和局部的研究模式［8］，以大范围采场为研究对象，借鉴应力拱理论［9］对采动条件下覆岩层的渗透特性进行了定性分析，得出覆岩渗透率的变化规律，采用物理模拟与数值模拟相结合的研究手段，获得采动覆岩渗透率演化的定量预测。

1 相似模拟实验

1.1 实验模型的建立

实验以王坡煤矿为工程背景，合理选择各相似系数，最终确定几何相似系数αL=200，时间相似系数αt=14.1，煤岩视密度相似系数αr=1.8，岩石强度相似系数ασ=360。根据相似常数以及现场柱状图，获得研究采面煤层上下关键层位统计表，并对骨料进行配比。试验台长×宽×高为1000mm ×900mm×300mm。覆岩重力采用柔性加载方式施加于模型上部边界，能够更好地再现现场赋存条件。实验台前后对应位置设计有可控开关的导气孔，实现对覆岩渗透率定量测定。同时在铺设模型的过程中在各测点布置应力监测装置，采用DDS型准静态数据采集仪进行数据采集，整个实验装置具有良好的密闭性。

1.2 实验过程

对气密性进行检测后，分别对各试验台前后对应导气孔进行通气，任一测点通气时，其他测点保持密闭状态。根据标准MT 223－90给出的煤岩样试件空气的渗透率测定方法［10］，模型渗透率公式:

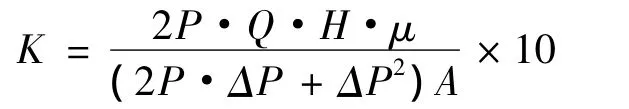
式中，K为渗透率，m2;P为出口端气压力，Pa; Q为渗流量，mL/s;H为模型宽度，mm;μ为气体动力黏度，Pa·s;A为模型每测孔等效面积，mm2。

通过计算得出模型各点随开采变化的渗透率，进而建立各测点的渗透率变化曲线。同时由数据采集仪得到各测点随采动变化的垂直应力数据。

1.3 数据处理与分析

本次试验设置4个测点，分析各监测点渗透率与垂直应力的数据，通过非线性曲线拟合 (如图1)，发现所模拟覆岩渗透率受采动影响，与垂向应力关系表达式符合如下形式:

式中，ΔK为相对渗透率，是渗透率与初始渗透率比值，即ΔK=K/K0，K0为初始渗透率，m2;Δσzz为垂向应力变化量，MPa;a，b，c分别为拟合常数。

图1 渗透改变与垂向压力变化曲线拟合

各拟合常数及R2见表1。拟合曲线参数总体均符合指数函数表达方式，均方差都在0.85以上。

表1 拟合函数各系数

2 采动覆岩应力与渗透特性耦合效应分析

根据前述实验得出的应力与渗透率之间的耦合关系，由前人的研究［11］结果可知岩层渗透率由垂向和水平向分渗透率组成，经推广后得出

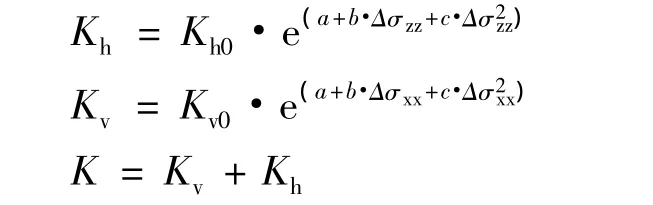
式中，Δσzz，Δσxx分别为垂向和水平向应力变化值，MPa;下脚标为0的代表其初始值。K为围岩总渗透率，m2。该结论与前人总结的不考虑瓦斯孔隙压力的渗透率与应力的基本公式K=a· exp(f(σ))形式相同。

数值模拟分析解决一般单物理场问题的思路是根据连续介质理论，引入本构关系以及通过牛顿定律、动量和能量守恒方程得出的控制方程来模拟所研究的工程问题，当考虑涉及多物理场之间相互作用对需解决的问题影响时，就需要引用耦合分析。通常耦合的方式有2种，即全耦合和半耦合［12］。

受采动影响，上覆围岩应力变化特征明显，裂隙也呈现一定由压密—产生—扩展—闭合的分区特征。在此过程中，赋存在煤岩体内的瓦斯由于区域内孔隙压力的降低，导致吸附的瓦斯解吸，因为局部围岩应力的释放及裂隙扩展产生瓦斯流动通道，导致采煤工作面涌出瓦斯以及邻近煤层瓦斯向采空区及采煤工作面集中，造成瓦斯超限等威胁影响煤炭正常回采。此过程就是一个多物理场耦合的过程，因此可以用顺序耦合的方式，引入上覆围岩应力与渗透率之间的定量关系来研究受扰动影响的覆岩渗透特性分布规律。

3 覆岩应力与渗透特性数值试验研究

3.1 计算模型的建立及网格参数的设置

根据工程背景，选取FLAC3D内置ss模型，模拟随工作面推进过程中，上覆围岩应力以及渗透率变化规律，其中渗透的分布规律主要是利用fish语言编写程序。由于应力的改变引起渗透规律在覆岩中的变化，从整体把握因应力改变导致渗透率的变化规律，该过程属于顺序耦合，即利用模拟得到的应力数据，通过利用前述总结的应力与瓦斯耦合的指数函数关系得出渗透率的变化规律。

当工作面推进一定距离，采场内采空区上方形成一定支承结构，是宏观裂隙拱在拱脚前移过程中的承载体，因此，在数值模拟过程中，对采空区采取煤矸石材料填充处理，更接近工程实际，其中采空区矸石的模拟模型采用双屈服模型。

由于各个岩层的初始渗透特性不同，将具有不同岩性的煤岩体初始渗透率通过fish语言程序提供给后期渗透分布规律的研究中，表2为不同岩性初始渗透数据。

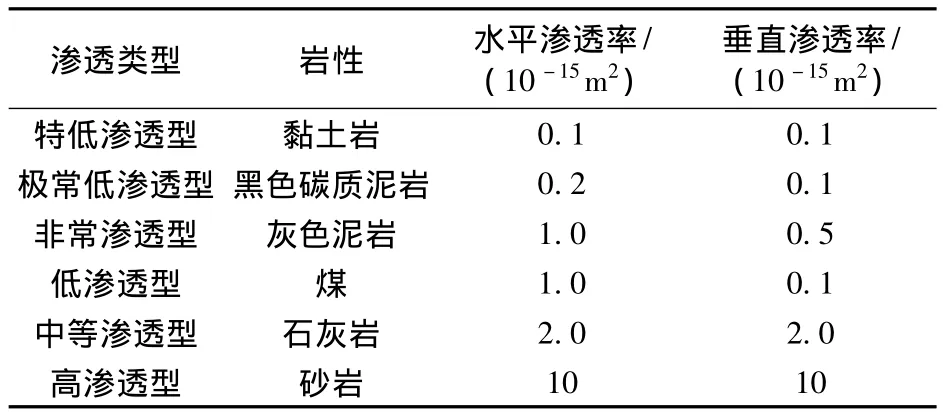
表2 不同岩性煤岩体初始渗透率

建立的几何模型为320m×200m×60m(长×高×宽)，采煤工作面长为160m，两侧煤柱分别为80m，共模拟开采煤层上16个岩层以及底板5个岩层，采用平面应变分析形式对模型四周进行约束，即模型的左右两侧、前后两侧及底面限制位移、速度为零;模型的上边界采用自由边界处理，并在此基础上施加均布荷载 (该荷载为上覆围岩折算载荷)，设置最大不平衡力监测，随时查看模型是否达到平衡阶段。

3.2 数值试验结果分析

根据文献 ［13］表述，地应力改变10MPa，相应的渗透率将有一个数量级的改变，并且由于储层的层状赋存条件，水平渗透特性的变化较垂向渗透特性的变化对应力的敏感性更强，此特征具体表现见采动影响渗透规律分布云图2至云图5(为便于比较，云图中的数值单位均为毫达西，1md≈1 ×10－15m2)。

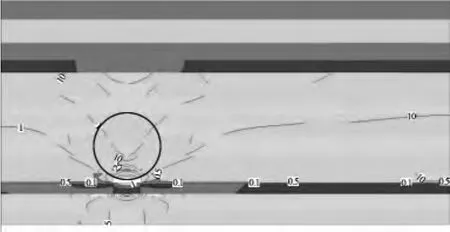
图2 工作面推进20m覆岩渗透规律分布

图3 工作面推进40m覆岩渗透规律分布

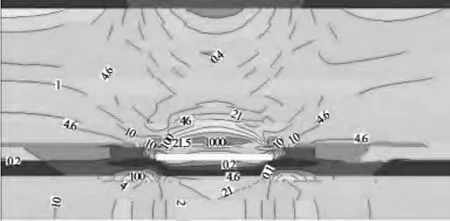
图4 工作面推进60m覆岩渗透规律分布

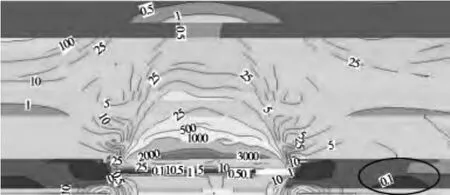
图5 工作面推进100m覆岩渗透规律分布

开采初期，由于采空区上方悬露面积较小，此时上方岩梁对其所起的承载作用较强，表现为梁效应。由组合梁理论［14］可知，此时上覆围岩应力主要由梁结构承担，并且组合梁低位承载力较大，高位承载力较小。由于岩梁弯曲，致使弯曲端顶部受到较大拉力，在岩梁结构上表现为松散，渗透特性增强。弯曲端内侧处于压缩状态，但由于岩梁整体下沉出现卸压，岩梁弯曲端顶部内侧出现压缩与卸压相互抵消，造成渗透特性没有发生变化 (如图2中小圆圈所示)。在开采初期，岩梁效应产生的渗透特性规律整体表现为漏斗状，由下至上，由外侧至内侧，渗透特性的减弱程度逐渐淡化。

随工作面推进，顶板下沉量继续增大，上覆岩体所表现出的整体特性进一步增强，各岩层之间的相互作用表现更为明显。漏斗状影响范围继续像周边扩展，开口度逐渐变大，致使上方梁结构不断向高位扩展。与此同时，应力拱对上覆岩体的支撑作用逐渐增强。拱顶向上发展并最终与梁相切，应力在拱顶集中 (如图3中小圆圈所示)，致使拱顶处渗透特性明显减弱。由此提出“拱上梁”假设，“拱上梁”力学结构模型合理地解释了前人基于应力拱理论研究中，应力拱结构中各受力点应力分布的差异，即拱角处应力最大，拱顶处次之，拱肩处最低。在“拱上梁”力学模型中，上覆岩体的重力由拱与梁共同承载。

工作面继续推进，致使顶板大面积垮落，拱梁结构呈现整体向上发展特性，在其发展过程中，拱的高度与跨度不断增大。当达到某一值时拱梁结构的影响范围趋于稳定 (如图5)，最终拱梁结构以相对稳定的高度与跨度周期性向前推移。覆岩规律表现为拱内覆岩渗透特性向纵深方向减弱，拱顶渗透特性减弱程度最为明显。拱脚位于工作面前方(如图5小圆圈所示)，致使工作面前方一定距离内发生明显渗透特性减弱现象。其次工作面前方支承压力区也发生一定范围的减弱现象。

模拟结果表明，超前钻孔布置的位置主要集中在工作面上方的“高导、高透、高渗”区域，并靠近工作面一侧。数值模拟分别对不同岩性、不同储层厚度进行独立的分析，得出的云图结果更符合现场实际，便于为现场相关工程的实施提供指导和借鉴。

4 结论

提出了同一采场下，以采空区长度确定不同的力学模型的分析方法，改变了原有对于同一采场只具有单一力学模型的看法。在对数值试验分析的基础上，参考应力拱理论提出在采空区上方存在的“拱上梁”力学结构模型。

(1)基于物理模拟实验数据得出表征覆岩水平渗透特性和垂直渗透特性的渗透率与应力的函数公式。利用得到的指数公式，将渗透率与应力关系引入数值试验模型，克服了实验室测点不连续所造成的对于渗透特性整体把握的困难。

(2)通过对渗透特性的应力敏感分析，得到开采不同阶段，上覆岩体具有不同的力学承载模型，各力学结构模型对于上覆岩体的承载作用是不断演化的，并最终推演提出“拱上梁”假说。

(3)获得采动覆岩渗透特性演化规律，得出了渗透特性在开采初期分布呈现漏斗状，由下至上，由外侧至内侧，渗透特性的减弱程度逐渐淡化的特点。伴随着工作面的推进，漏斗开口度逐渐变大，直至顶板发生第一次垮落，“拱上梁”结构起到了主要承载作用。各点渗透特性发生转变，拱内渗透特性向纵深方向递减，拱脚、拱壁、拱顶由于应力集中产生明显的渗透特性减小现象。

［1］钱鸣高，缪协兴，许家林，等.论科学采矿［J］.采矿与安全工程学报，2008，25(1):1－10.

［2］盛金昌，速宝玉.裂隙岩体渗流应力耦合研究综述［J］.岩土力学，1998，19(2):92－98.

［3］Ewy R T，Cook N G W.Deformation and fracture around cylindrical openings in rock—I.observations and analysis of defornations［J］.Int.J.Rock Mech.Min.Sci.，1990，27(5):387－407.

［4］林崇德.层次分析法在回采巷道支护形式选择中的应用［J］.岩石力学与工程学报，1990，9(3):244－251.

［5］林崇德.层状岩石顶板破坏机理数值模拟过程分析［J］.岩石力学与工程学报，1999，18(4):392－396.

［6］麻凤海，范学理，王 嘉.岩层移动动态过程的离散单元法分析［J］.煤炭学报，1996，21(4):388－392.

［7］陈荣华，白海波，冯梅梅.综放面覆岩导水裂隙带高度的确定［J］.采矿与安全工程学报，2006，23(2):220－223.

［8］李春睿.高强度开采覆岩裂隙场时空演化规律与瓦斯流动关系的研究［D］.北京:煤炭科学研究总院，2009.

［9］杨 科，谢广祥，常聚才.不同采厚围岩力学特征的相似模拟实验研究［J］.煤炭学报，2009，34(11):1447－1450.

［10］MT 223－90.煤和岩石渗透率测定方法［S］.1990.

［11］黄庆享，钱鸣高，石平五.浅埋煤层采场老顶周期来压的结构分析［J］.煤炭学报，1999，24(6):581－585.

［12］张旭辉，袁明道，潘展钊.顺序耦合分析在复杂结构热分析中的应用［J］.广东土木与建筑，2008，3(3):14－15.

［13］Ren，I.X.and J.S.Edwards.2002.Goaf gas modeling techniques to maximize methane capture from surface gob wells［J］.Mine Ventilation:279－286.

［14］钱鸣高，石平五.矿山压力与岩层控制［M］.徐州:中国矿业大学出版社，2003.

［15］李宏艳，王维华，齐庆新，等.煤与瓦斯共采覆岩应力及渗透耦合特性实验研究［J］.煤炭学报，2013，38(6):942－947.

［16］李 涛.陕北煤炭大规模开采含隔水层结构变异及水资源动态研究［D］.徐州:中国矿业大学，2012.

［17］刘 洋.浅埋煤层开采矿井涌水量计算方法研究［D］.西安:西安科技大学，2012.

［18］朱 涛.软煤层大采高综采采场围岩控制理论及技术研究［D］.太原:太原理工大学，2010.