基于目标几何中心的高分辨雷达角跟踪方法
孙迎丰,刘旭东,张 磊,王新政
(海军航空工程学院,山东烟台 264001)
0 引言
雷达导引头在成功截获目标后,需要由搜索状态转入对目标的自动跟踪状态。对于雷达导引头的角跟踪而言,目标角闪烁是主要的误差源。尤其当导弹与目标处于相对高速运动状态时,角闪烁影响更为严重,如若不能对其进行有效处理,就难以保证雷达导引头对目标角跟踪的稳定性和精确性。因此研究角闪烁背景下的目标角度估计和跟踪问题对于提高雷达导引头的制导精度有着极为重要的意义。
根据角闪烁产生机理研究[1],角闪烁是由复杂目标不同部位的散射回波相互干涉而形成的测角误差。经典的角闪烁抑制方法是根据不同的雷达体制和应用背景,对目标的散射回波进行分集接收和滤波处理。随着雷达技术的发展和应用,基于高分辨的单脉冲测角方法在抑制角闪烁和精确制导等方面具有较大的潜力。文献[2]分析了高分辨距离像中散射点在距离单元中的分布及其角闪烁特征;文献[3]提出了基于高分辨距离像的单脉冲角跟踪方法。文献[4]验证了目标几何中心对角跟踪的影响。以上研究的思路基本相同:利用高分辨处理将目标的散射单元尽可能分开,减少散射单元之间的相互干涉;对目标在各个分辨单元的角度信息进行幅度加权,将得到的角度估计用于后续跟踪等处理。
基于高分辨的单脉冲测角方法是抑制角闪烁、提高角跟踪性能的有效途径。现有研究采用幅度加权的思路,在对目标角度的估计过程中只利用了目标多个散射点的幅度信息。在距离高分辨条件下,散射点的距离信息表征了目标散射点在径向上的分布情况,对目标几何中心的角度估计更具有实际意义。因此,本文充分利用高分辨雷达所能提供的有效目标信息,提出基于目标几何中心的角度信息处理方法,并通过仿真验证该方法的角跟踪性能。
1 复杂目标的散射中心模型
根据雷达目标特性研究[5],当雷达工作波长远小于目标尺寸时,目标表现出很强的局部散射特性,可以用散射中心模型描述。复杂目标可作为若干独立散射中心的集合来处理,雷达发射信号受各散射中心延迟和幅度调制后,形成散射中心子回波,目标回波即是各散射中心子回波的矢量和。
设雷达发射信号为s(t)=u(t)·exp(j2πfct),其中,u(t)为发射信号复包络,fc为雷达工作频率。假设目标上有M个散射中心,若在一个脉冲周期内,目标相对雷达的姿态不变,则目标回波信号可表示为
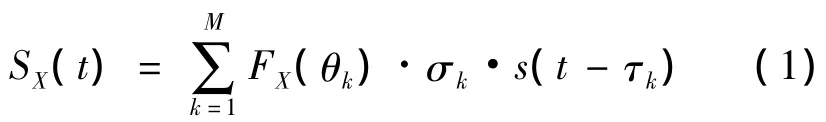
式中,FX(θ)表示天线方向性函数,对于单脉冲天线,下标X=Σ或X=Δ分别对应单脉冲天线和差波束分别为第k个散射中心的角度、散射强度、回波延迟和径向距离;c为电磁波传播速度。
现代雷达通常采用大时宽带宽积信号以提高系统探测能力,其中线性调频(LFM,linear frequency modulation)脉冲信号因其优良性能得到最为广泛的应用[6]。LFM脉冲信号通过在脉冲持续时间内信号频率的连续变化获得较大的信号带宽。对于LFM脉冲信号,其复包络为

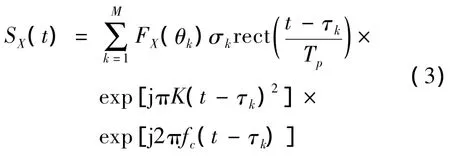
雷达系统需要对接收的回波信号采用基于匹配滤波的脉冲压缩技术实现距离高分辨。当距离分辨率远小于目标尺寸时,目标回波的距离像包含了目标几何结构和物理特性的细节信息,将有利于目标的识别和跟踪。
2 振幅和差单脉冲测角原理
单脉冲测角是一种成熟的雷达角度测量技术,具有快速获取高精度角信息的能力,跟踪制导雷达多采用该技术,其中应用最广泛的是振幅和差法。其测角原理是在同一角平面内形成两个形状相同并对称于天线轴线的倾斜波束,对两波束同时接收的信号进行和差处理,从中获取目标偏离天线轴的角度信息。
设两个波束的方向性函数为F(θ),与天线轴线的倾斜角为±θ0,和、差波束方向图函数分别为FΣ(θ)和 FΔ(θ),则有
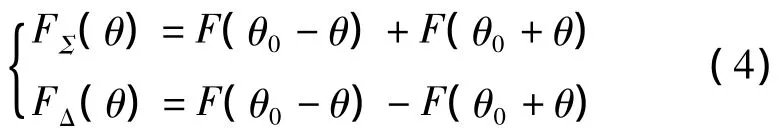
目标回波经单脉冲天线接收并输出的和信号SΣ(t)与差信号SΔ(t),分别送入单脉冲接收机的和通道、差通道进行混频及中频放大等处理,得到两通道输出的信号为
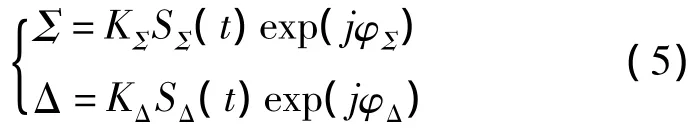
式中,KΣ、KΔ分别为和、差通道的信号传输系数;φΣ、φΔ分别为和、差通道中的相移。
经分析可知,当目标偏离等天线轴的角度不大时,差信号Δ的幅度与偏离角的大小成正比;为消除回波幅度变化的影响,需要利用和信号Σ对差信号Δ进行幅度归一化处理,其比值大小与目标偏离角呈线性关系,和差信号的相位差也与目标偏离角的方向相关。
因此,通过对和差通道输出信号的幅相比较,可以得到目标相对于天线轴线的偏离角,即单脉冲角度测量公式为

式中,φ为和差信号的相位差,理想情况下,其取值为0 或180°。
3 基于角闪烁抑制的角跟踪信息处理方法
对于LFM脉冲体制,需在测角前先对目标回波脉冲压缩匹配滤波。因此,单脉冲雷达导引头角度信息处理框图,如图1所示。
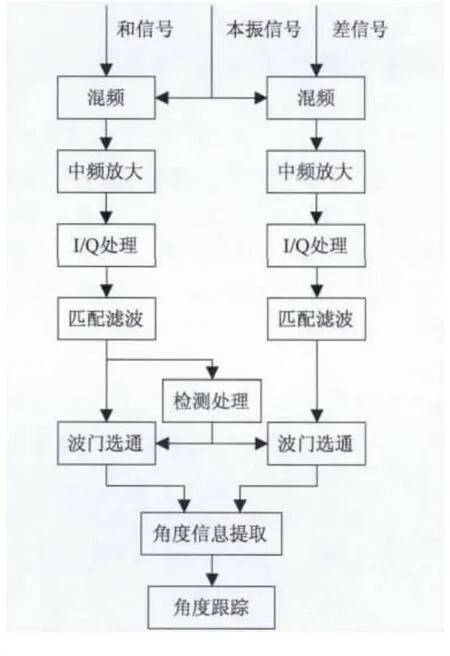
图1 单脉冲雷达导引头角度信息处理流程框图
首先在和差通道分别进行脉冲压缩匹配滤波,并在和通道的高分辨距离像上实现目标强散射点距离单元的检测。然后,根据单脉冲测角算法,结合差通道距离像,求出幅度超过检测门限的散射点的角度,然后对各个散射点的角度测量数据进行融合处理,估计目标角度并用于角跟踪。
3.1 基于信号幅度加权的处理方法
早期的雷达导引头由于分辨率较低,不能区分目标的各个散射中心,通常只能以目标回波中最强散射位置的角度作为对目标角度的估计值。这种方法实现简单,但是由于回波幅度会随弹目的相对运动或姿态改变而起伏不定,角闪烁引起的测角误差偏大,从而难以稳定跟踪。由于单脉冲测角能提供远高于角跟踪系统所需的数据率,因此,可利用角闪烁与回波幅度之间的负相关性[5],对多个脉冲的角度测量值进行幅度加权,减小角闪烁误差的影响。
在距离高分辨率条件下,目标散射中心在一定程度上被分离到不同的距离单元中,故雷达导引头可获得目标在多个距离单元上的角度值,这正是高分辨雷达提供的技术优势。然而,现有研究方法多是继承幅度加权的思想,对多个距离单元的测角结果进行加权处理,以抑制角闪烁,提高测角精度,进而改善角跟踪性能。
假设由单脉冲测角处理得到的角度测量为θi(i=1,2,…,N),N 为测量值数目,幅度加权处理公式为

平均加权:W(ai)=1
最大幅度加权:W(ai)=δ(ai-amax)
其中,amax=max{ ai},i=1,2,…,N。
3.2 基于目标几何中心的处理方法
由上文分析易知,从距离高分辨雷达的目标回波中可以获取的信息包括散射点的距离、散射点的角度及散射点的回波幅度。不难看出,在对目标角度的估计过程,现有方法利用了散射点的幅度信息,而忽视了散射点的距离信息。
目标几何中心一般是指由其形状特征确定的目标区域内某一点。对于雷达目标的角度估计和角度跟踪而言,目标几何中心具有确切的物理意义。在距离高分辨条件下,散射点的距离信息表征了目标散射中心在径向上的分布情况,属于目标几何形状的相关信息。可见,距离信息对于目标几何中心的角度估计具有实际意义。
基于以上分析,提出了基于目标几何中心的处理方法:首先利用散射点的幅度信息进行数据筛选,使角闪烁误差较大的值得到有效抑制;然后,利用距离信息对目标几何中心的角度估计,作为目标角度的测量值输出并用于角跟踪。
假设获取的目标信息为 Ω = {(ri,θi,ai,bi)},i=1,2,…,N,其中,ri、θi、ai和 bi分别为第 i个散射点的距离、角度、和信号幅度和差信号幅度。根据单脉冲天线和差方向图特性,可利用和、差信号幅度对目标信息进行筛选,即

式中,k0是由单脉冲天线和差方向图决定的参数。雷达测量是在极坐标下进行,且距离和角度信息相互独立。通过将极坐标下的测量信息转换至直角坐标系下,即将距离和角度的信息进行耦合,则能有效利用距离高精度测量的特点。
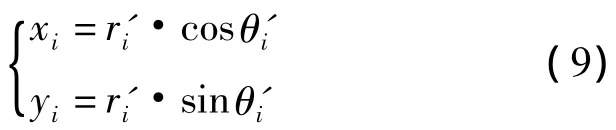

则目标几何中心的角度估计为

该方法充分利用了高分辨雷达获取的目标信息,可在一个脉冲周期内得到目标几何中心的准确估计,对于提高目标角度的测量精度和稳定跟踪都将带来较大的改善。
4 仿真实验分析
为了验证所提方法的有效性,本文采用信号仿真方法对雷达导引头接收和信息处理全过程进行了建模与仿真,该模型具有较高的仿真精度,能满足角度跟踪性能仿真需要。
仿真场景为雷达制导的反舰导弹攻击舰船目标。采用文献[7]提供的舰船散射中心分布模型,如图2所示,舰船长约150 m,宽约30 m。

图2 舰船多散射中心分布图
仿真实现的振幅和差式单脉冲雷达导引头采用LFM脉冲压缩体制,主要参数为:工作频率X波段,LFM信号的脉冲宽度为10 μs,带宽为10 MHz,对应的距离分辨率为15 m;天线波束3 dB宽度为5°,距离跟踪采用α-β滤波算法。假定整个攻击过程中,舰船不实施任何电子干扰,以均匀速度直线航行,导弹飞行速度为300 m/s,比例导引系数为3.7。雷达导引头在距舰船7 km处转入跟踪状态,不同处理方法下的角跟踪误差曲线,如图3所示。
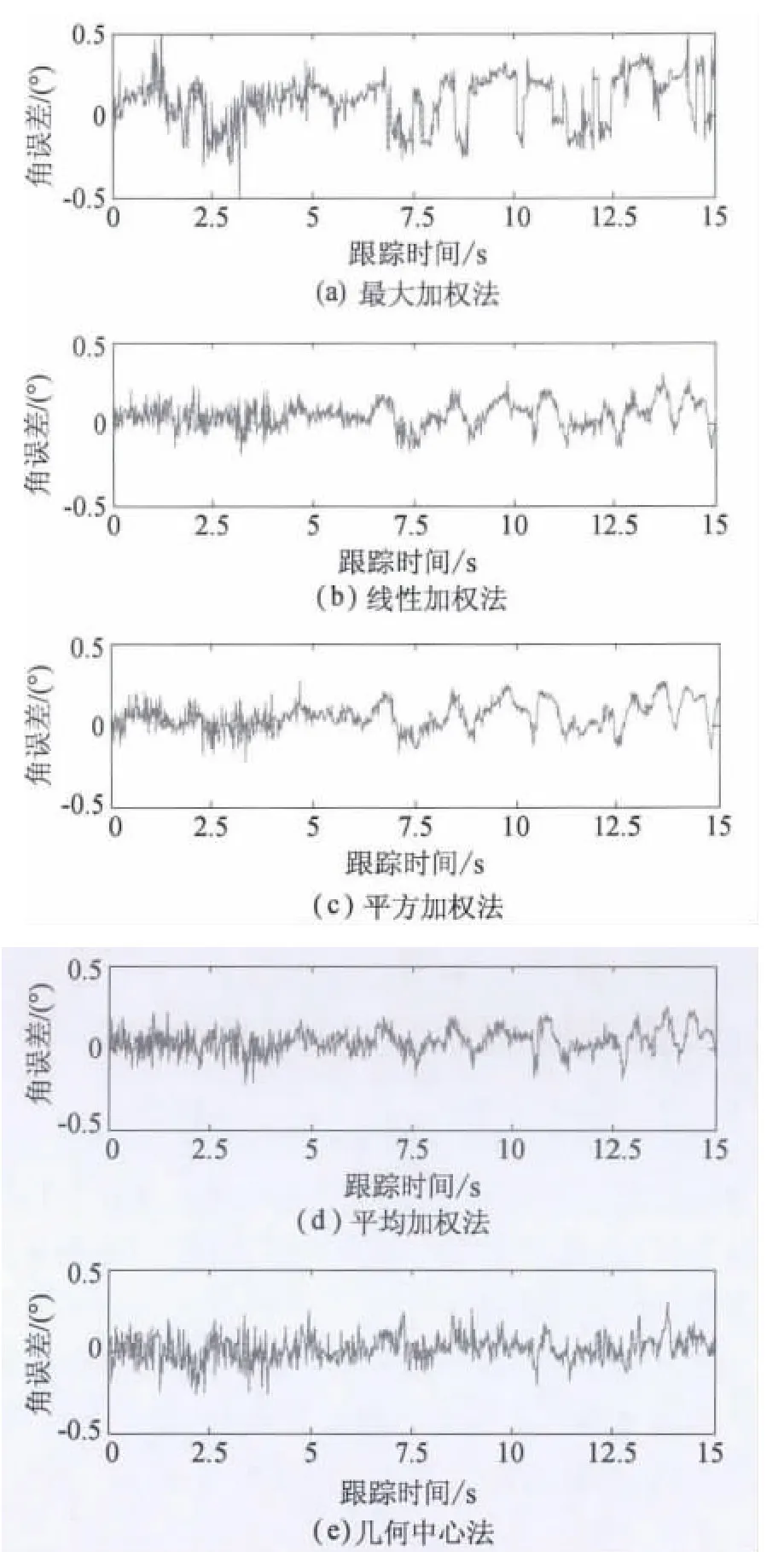
图3 不同处理方法下的角跟踪误差
由于舰船目标尺寸较大,相对而言雷达距离分辨率比较高,舰船的散射中心在一定程度上被分散开。由图3可以看出:
(1)最大加权法的角误差起伏较大,这是因为弹目之间相对高速运动,目标回波幅度易随目标相对雷达的姿态变化而起伏不定,所以,最大加权法的角跟踪稳定性较差。
(2)线性加权、平方加权和平均加权等三种处理方法,相较于最大加权法,它们都综合了目标多个散射点的幅度信息,角误差的起伏较小,角跟踪性能有明显改善。需要指出,由于仿真中舰船各散射中心分布较为均匀,散射强度也采用均匀分布模型,所以,平均加权法的性能要优于前两种方法。但实际情况下,目标的散射特性将更为复杂,平均加权法的性能有待进一步验证。
(3)由于距离分辨率有限,目标各散射中心之间的相互干涉仍然存在。线性加权、平方加权和平均加权等三种处理方法,尽管其角误差起伏较小,但在跟踪过程中表现出非平稳特性(见图中6 s以后的角误差数据)。而几何中心法有效利用了散射点信息,角误差的起伏较小,而且具有平稳性,这一点将有利于保证角跟踪的稳定性。
各种处理方法对应的角跟踪误差的均值和标准差,见表1,从统计数据也可以看出,几何中心法的跟踪性能要优于其它几种处理方法。
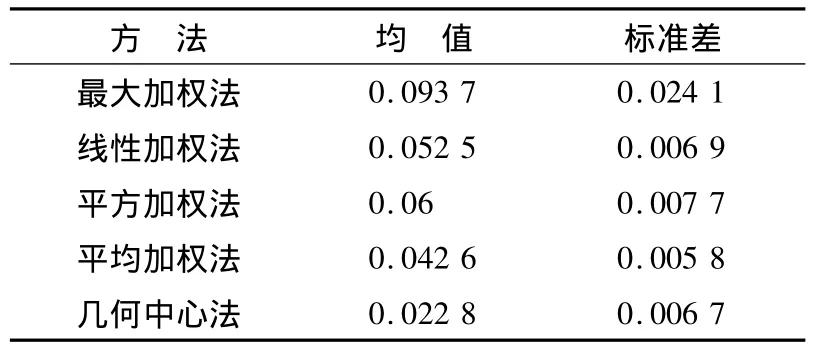
表1 不同处理方法下角跟踪误差统计数据
5 结语
本文研究了距离高分辨体制的雷达导引头角度信息处理方法,充分利用距离高分辨技术与单脉冲高精度测角技术所获取的目标信息,提出了基于目标几何中心的角信息处理方法,并通过仿真验证了该方法具有较好的角闪烁抑制性能,并提高了角跟踪精度和稳定性。必须指出的是,本文仅讨论了角闪烁背景下的角跟踪问题,对于复杂电子干扰背景下的雷达导引头角跟踪性能,有待进一步验证。
[1] 张治西,张锐娟.角闪烁抑制和利用问题的探讨[J].现代雷达,2009,31(12):14-18.
[2] 张涛,张群,马长征,等.基于高分辨距离像的角闪烁抑制方法[J].西安电子科技大学学报,2001,28(03):296-300.
[3] 赵宏钟,何松华.基于高分辨距离像的单脉冲角跟踪技术[J].电子学报,2000,28(4):142-144.
[4] 王文民,曹伟,苏宏艳.基于幅度加权几何中心法的毫米波高分辨雷达角跟踪技术[J].电讯技术,2009,49(02):64-67.
[5] 李保国,马君国,赵宏钟,等.毫米波单脉冲雷达高精度测角算法研究[J].系统工程与电子技术,2005,27(10):1673-1675.
[6] 胡体玲,李兴国.几种制导用高分辨雷达信号分析[J].弹箭与制导学报,2007,27(03):247-250.
[7] 张安,卢再奇,范红旗,等.基于散射中心模型的舰船LFM雷达回波仿真[J].雷达科学与技术,2011,9(04):316-320.

