渗透系数空间变异性对低渗透地层中地下水溶质运移的影响

王 超，束龙仓，鲁程鹏

(河海大学水文水资源学院，江苏南京 210098)

渗透系数是表征地层水力特性的重要参数，影响着地下水溶质的分布和运移特征［1］。已有研究表明渗透系数在空间上的分布具有空间变异性，且很难通过实际测量获取区域中所有位置的参数值。早在20世纪70年代，Freeze［2］通过统计大量渗透系数实测数据得到其空间变异特征，认为多孔介质渗透系数的空间分布可以用对数正态分布函数来描述，这一结论随后被许多学者证实和采用［3-6］。很多研究证明渗透系数的空间变异性会对地下水溶质运移产生影响［7-9］，但目前在低渗透地层中对该方面的研究较少。低渗透地层中地下水的溶质运移对滨海地区水库水质咸化有重要影响［10］，而地层渗透系数的空间变异性又影响着溶质运移的过程。笔者以天津市北大港水库为例，基于库底地层渗透系数实测资料，研究渗透系数的空间变异性，并利用地下水数值模拟软件Visual ModFlow研究库底地层渗透系数空间变异性对地下水溶质运移的影响。

图1 北大港水库地理位置示意图Fig.1 Geographic sketch map of Beidagang Reservoir

1 北大港水库概况

北大港水库位于天津市滨海新区南部大港境内(图1)，地处海河流域的大清河、南运河、子牙河水系的独流减河下游右岸，蓄水面积为152.5 km2，围堤总长为54.511 km。

北大港水库位于冲积海积平原，水域面积大，蒸发浓缩作用强。浅层地下水水位季节变化明显，化学类型为Cl-Na，矿化度高，是典型的海滨相成因咸水。

水库运行20多年来，由于上游水资源条件的变化，蓄水量大幅度减少，甚至连年干枯，同时水库也存在着蒸发渗漏损失大、水质咸化、水资源利用率低、生态环境恶化等一系列问题，水库正常功能和效益的发挥受到极大影响。为改变北大港水库运行现状，拟通过修建南北隔堤将水库分为东、西两库。

2 分析方法

笔者通过野外勘探、现场取样、室内试验、数值模拟等方法，研究北大港水库西库在挖深1 m后库底地层渗透系数空间变异性对地下水溶质运移(以Cl-为模拟因子)［11］的影响。

2.1 渗透系数的测定

由于库底地层多为粉质黏土，渗透系数小，因此利用渗透仪进行室内变水头渗透试验测定不同深度钻孔岩芯原状土样的渗透系数［12］。野外现场勘探共设钻孔26眼，分布于水库西库库区与库周，对钻孔岩芯进行分层取样，共计121个原状土样。

基于达西定律，渗透系数的计算公式为［13-14］

式中:K——土样的渗透系数，m/d;A1、A2——土样和测压管的截面面积，m2;Lv——渗透仪内土样的长度，m;h1，h2——t1和t2时刻进水管内相对于渗透仪出水口的水头值，m。

图2 库底地层渗透系数随深度变化Fig.2 Variation of hydraulic conductivity of bottom stratum of reservoir with depth

通过分析121个土样的渗透系数，可知库底地层渗透系数空间分布较为分散，变化范围为10-6～10-2m/d(图2)。同一深度，不同位置土样渗透系数差别显著，极大与极小者相差4个数量级。依据岩性将土样分为2组，分别是深度0～4 m的陆相粉质黏土和4 m以下的海相粉质黏土。陆相粉质黏土层渗透系数范围为2.62×10-6～3.31×10-3m/d，平均值为1.77×10-4m/d，普遍小于海相粉质黏土的渗透系数(分布范围为1.78×10-6～1.06×10-2m/d，平均值为2.73×10-3m/d)。

2.2 渗透系数随机分布特征

由于渗透系数空间分布描述主要表现为对数正态分布或正态分布，因此笔者利用P-P概率图对2组土样的渗透系数分别进行正态分布和对数正态分布检验，结果如图3所示。

P-P概率图是由理论分布期望累积概率值与变量假设分布累积概率值构成的散点图，用于检验变量分布。若数据点分布在一条从纵轴零点指定右上角的直线上，说明此数据系列服从所要检验的分布类型［12］。

由图3可知，相对于正态分布，对数正态分布能更好地对渗透系数进行拟合。因此，在渗透系数空间变异性对地下水溶质运移影响的研究中，将渗透系数设置成符合对数正态分布的随机场。

2.3 数值模型的建立

为研究渗透系数空间变异性对地下水溶质运移的影响，笔者通过改变渗透系数对数场的均值(K'AVE)与

图3 渗透系数P-P概率图Fig.3 P-P plot of hydraulic conductivity

标准差(K'STD)模拟地层中溶质浓度均值与标准差的变化。

2.3.1 数学模型

根据水库库底地层水文地质条件，建立一维潜水非稳定流运动数学模型:

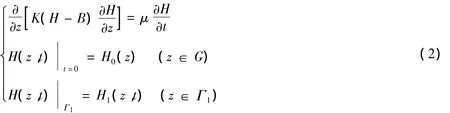
式中:H——潜水水位，m;B——含水层底板高程，m;μ——给水度;H0——初始水位，m;H1——边界上的水位，m;G——模拟区域;Γ1——一类水头边界。

溶质运移数学模型:

式中:c——溶质质量浓度，mg/L;h——含水层饱和厚度，m;n——有效孔隙度;D——水动力弥散系数，m2/s;S——浓度边界。

地下水流运动与溶质运移分别采用Visual ModFlow中的MODFLOW和MT3DMS模块进行模拟。

2.3.2 时空离散

数值模型模拟的范围为北大港水库西库区，库底表面为上边界，库底以下8.2 m为下边界。平面上有效网格数为2190个，单位网格大小为183 m×245 m。垂向上共分为10层。其中第1层与第10层分别为上、下边界，厚度均为0.1 m，其余各层厚度均为1 m。第1～5层为陆相粉质黏土层，6～10层为海相粉质黏土层。

模型模拟期为10 a，划分为10个应力期，并在每个应力期内按增长因子1.2将其进一步划分为10个步长递增的时间段。

2.3.3 初始条件

利用稳定流情况下的地下水流场与浓度场作为非稳定流模型的初始条件。由于库底表层与水库水体直接接触，因此稳定流模型中第1层的地下水水位和Cl-质量浓度与水库水体一致，分别为5.5 m和50 mg/L;第10层地下水水位与Cl-质量浓度取多次监测平均值，分别为2.5 m和5070 mg/L。

2.3.4 边界条件

为简化模型，将模型第1层和第10层作为定水头与定浓度边界，其水头和浓度值与初始条件一致。

2.3.5 水文地质参数

渗透系数按2.2节中的方法赋值，再利用模型模拟不同空间变异条件下的溶质运移过程。基于渗透系数实测值，笔者分别按一定幅度改变K'AVE和K'STD，以此来表示渗透系数不同的空间变异程度。

孔隙度、给水度等水文地质参数具有较小的变异性，模型中均采用粉质黏土的经验值。弥散度虽然也具有一定的非均质性和尺度效应［15］，但出于本文研究目的，在文中未考虑。

3 模拟结果及分析

模拟时在K'STD不变的条件下，K'AVE按幅度Δ=±10%、±30%、±50%进行改变;在K'AVE不变的条件下，K'STD按幅度Δ=±20%、±40%、±60%进行改变。模型分别模拟以上不同渗透系数条件下的地下水流与溶质运移情况。

3.1 地下水水流通量随渗透系数空间变异性的变化

将第10年年末地下水流通量取自然对数，记为lnQ，其随K'AVE和K'STD的变化如图4所示。

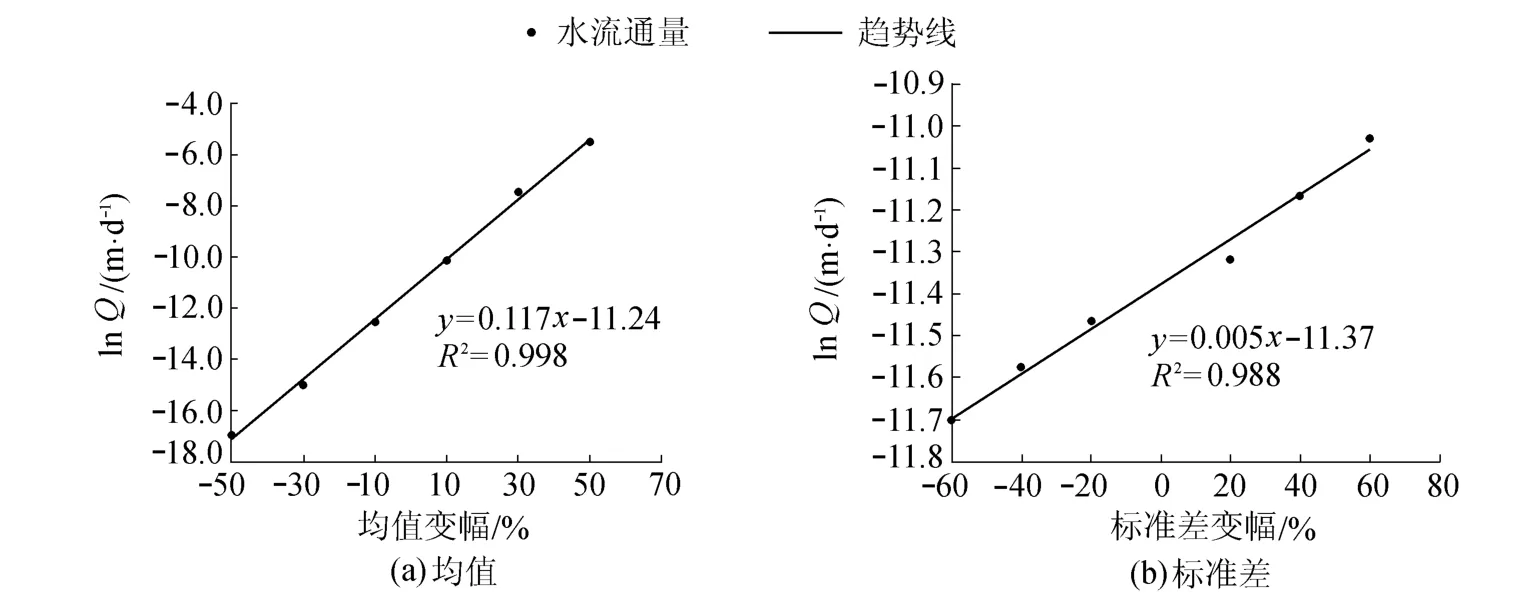
图4 地下水流通量随渗透系数自然对数场均值和标准差的变化Fig.4 Variation of flow flux with average natural logarithm and standard deviation of hydraulic conductivity

由图4可知，在第10年年末，地层中地下水流通量随K'AVE和K'STD的增大均呈现指数增长的趋势，且随K'AVE的变化更快。因此渗透系数对地下水流通量具有较大影响，且渗透系数均值的变化比标准差的变化对水流通量的影响更明显。

3.2 模拟期内地层中溶质总量随时间的变化

将模拟期(10 a)内每年的地层溶质总量取自然对数，记为lnM，在不同均值和标准差的渗透系数自然对数场条件下，溶质总量自然对数值随时间的变化如图5所示。

图5 不同渗透系数自然对数场条件下溶质总量自然对数值随时间的变化Fig.5 Variation of total solute mass with time under conditions of different natural logarithms of hydraulic conductivity

图5表明:地层中溶质总量随时间不断减小;在K'STD不变的条件下，溶质总量随其均值的增大而不断减小;在K'AVE不变的条件下，溶质总量随其标准差的增大而不断增大。由于K'AVE对地下水流通量的作用大于K'STD的作用，因此渗透系数均值增大的情况下地下水流通量增加。由于地下水位低于库水位，库水一直补给地下水，溶质运移受到地下水流的抑制作用，因此溶质质量随渗透系数均值减小;当渗透系数标准差增大时，地下水流的抑制作用相对较小，地层中溶质质量仍随之增加。

3.3 模拟期末地层不同深度处溶质质量浓度随K'AVE的变化

第10年年末地层不同深度处溶质质量浓度均值与标准差随渗透系数自然对数场均值的变化如图6所示，图中虚线表示北大港水库底地层实测渗透系数场条件下的溶质运移情况。

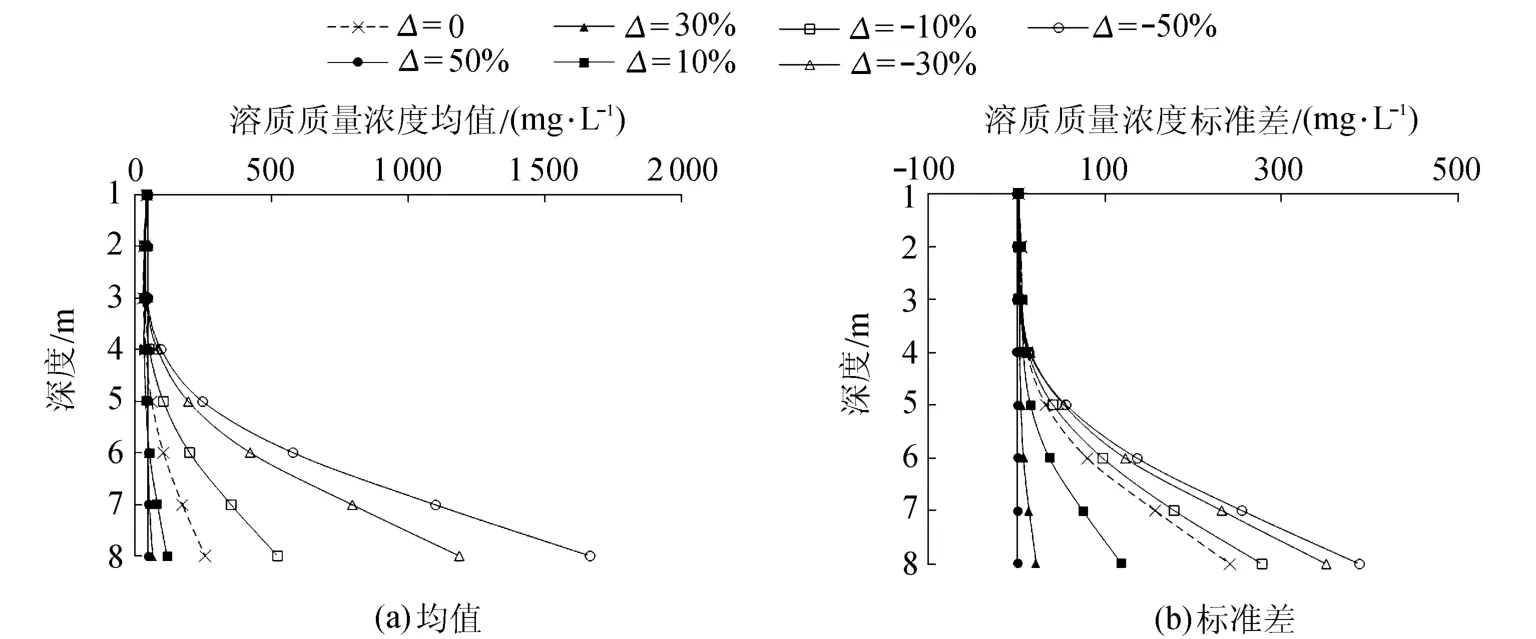
图6 库底地层不同深度处溶质质量浓度随K'AVE的变化Fig.6 Variation of solute concentration with K'AVE at different depths of bottom stratum of reservoir

由图6可知:随着K'AVE的增大，同一深度处溶质质量浓度的均值和标准差减小，不同深度处溶质质量浓度均值与标准差的差异越来越小;随着深度增加，地下水溶质质量浓度均值与标准差的变化幅度增大。这是由于库底地层整体的渗透性增加，地下水在水头差作用下自上而下的水流通量增大，加大了对溶质运移的抑制作用，同时由于下层库底地层的溶质浓度较高，地下水流的抑制作用相对明显，使溶质质量浓度均值与标准差的变化幅度较大。

3.4 模拟期末库底地层不同深度处溶质浓度随K'STD的变化

第10年末库底地层不同深度处溶质质量浓度均值与标准差随K'STD的变化如图7所示，图中虚线表示渗透系数自然对数场均值与标准差未做改变时的情况。

图7 库底地层不同深度处溶质质量浓度随K'STD的变化Fig.7 Variation of solute concentration with K'STD at different depths of bottom stratum of reservoir

由图7可知:随着渗透系数自然对数场标准差的增大，同一深度处溶质质量浓度的均值与标准差也在增大，不同深度处溶质质量浓度均值与标准差的差异也越来越大;随着深度增加，地下水溶质质量浓度均值与标准差的变化幅度增大。这主要是由于库底地层非均质性增强，渗透系数在空间上围绕均值变化的程度增加，对于渗透系数较大的区域，地下水流对溶质运移的抑制作用增强，而对于渗透系数较小的区域，地下水流的抑制作用变弱，溶质运移增强。综合模型结果来看，随着空间变异程度的增加，地下水溶质运移变强。

4 结 论

a.北大港水库底地层渗透系数较小，呈现出较强的空间变异性。陆相粉质黏土层渗透系数在2.62×10-6～3.31×10-3m/d之间，海相粉质黏土层渗透系数在1.78×10-6～1.06×10-1m/d之间，且均服从对数正态分布。
b.地下水流通量随着地层渗透系数的增加而增大，且在同样的渗透系数均值条件下，其空间变异程度的增加能够进一步增大地下水流通量。渗透系数均值对地下水流通量的影响比标准差大。
c.地层渗透系数空间变异性对地下水溶质运移具有较大影响。随着库底地层整体渗透性增加，溶质运移易受地下水流的抑制，溶质质量浓度较低，离散程度也较弱;若库底地层整体渗透性的空间变异程度增加，则地下水流对溶质运移的抑制作用相对减小，溶质质量浓度增加，其离散程度也随之增大。对于水库而言，渗透性较好且渗透系数空间变异程度较弱的库底地层有利于减小地下水对水库水质咸化的影响。

［1］陈彦，吴吉春.含水层渗透系数空间变异性对地下水数值模拟的影响［J］.水科学进展，2005，16(4):482-487.(CHEN Yan，WU Jichun.Effect of the spatial variability of hydraulic conductivity in aquifer on the numerical simulation of groundwater［J］.Advances in Water Science，2005，16(4):482-487.(in Chinese))

［2］FREEZE R A.A stochastic-conceptual analysis of one-dimensional groundwater flow in nonuniform homogeneous media［J］.Water Resources Research，1975，11(5):725-741.

［3］李伟，束龙仓.湖区地层垂向渗透系数概率分布特征分析［J］.水利水电科技进展，2005，25(2):20-22.(LI Wei，SHU Longcang.Probability distribution characteristics of vertical hydraulic conductivity in substrate of lake area［J］.Advances in Science and Technology of Water Resources，2005，25(2):20-22.(in Chinese))

［4］施小清，吴吉春，袁永生.渗透系数空间变异性研究［J］.水科学进展，2005，16(2):210-215.(SHI Xiaoqing，WU Jichun，YUAN Yongsheng.Study on the spatial variability of hydraulic conductivity［J］.Advances in Water Science，2005，16(2):210-215.(in Chinese))

［5］SUDICKY E A.A natural gradient experiment on solute transport in a sand aquifer:spatial variability of hydraulic conductivity and its role in the dispersion process［J］.Water Resources Research，1986，22(13):2069-2082.

［6］GELHAR L W.Stochastic subsurface hydrology from theory to application［J］.Water Resources Research，1986，22(9):135-145.

［7］梁婕，曾光明，郭生练，等.渗透系数的非均质性对地下水溶质运移的影响［J］.水利学报，2008，39(8):900-906.(LIANG Jie，ZENG Guangming，GUO Shenglian，et al.Effect of hydraulic conductivity heterogeneity on solute transport in groundwater［J］.Journal of Hydraulic Engineering，2008，39(8):900-906.(in Chinese))

［8］阎婷婷，吴剑锋.渗透系数的空间变异性对污染物运移的影响研究［J］.水科学进展，2006，17(1):29-36.(YAN Tingting，WU Jianfeng.Impacts of the spatial variation of hydraulic conductivity on the transport fate of contaminant plume［J］.Advances in Water Science，2006，17(1):29-36.(in Chinese))

［9］WU Jichun，HU B X，ZHANG Dongxiao，et al.A three-dimensional numerical method of moments for groundwater flow and solute transport in a nonstationary conductivity field［J］.Advances in Water Resources，2003，26(11):1149-1169.

［10］吴光红，李金中，李学菊.天津滨海地区城市供水调节水库水质咸化原因与改善途径［J］.水资源保护，2010，26(1):29-31.(WU Guanghong，LI Jinzhong，LI Xueju.Cause and prevention countermeasures of water salinization of city water supply reservoir in the coastal region of Tianjin［J］.Water Resources Protection，2010，26(1):29-31.(in Chinese))

［11］侯印伟，束龙仓，李广贺.关于地下水水质模拟中模拟因子选择的研究:以济宁市地下水水质模型为例［J］.长春地质学院学报，1990，20(3):297-300.(HOU Yinwei，SHU Longcang，LI Guanghe.Research on modeling factors selection in groundwater quality modeling-make an example of groundwater quality model in Jining City［J］.Journal of Changchun University of Earth Science，1990，20(3):297-300.(in Chinese))

［12］束龙仓，李伟.北塘水库库底地层渗透系数的随机特性分析［J］.吉林大学学报:地球科学版，2007，37(2):216-220.(SHU Longcang，LI Wei.Analysis on the stochastic characteristic of the hydrauic conductivity of bottom stratum，Beitang Reservoir，Tianjin City［J］.Journal of Jilin University:Earth Science Edition，2007，37(2):216-220.(in Chinese))

［13］TODD D K，MAYSL W.Ground water hydrology［M］.3rd ed.New York:John Wiley＆ Sons Inc，2002:95-96.

［14］FETTER CW.Applied hydrogeology［M］.4th ed.New Jersey:Prenticer-Hall Inc，2001:92.

［15］董书宁，戴振学，李竞生.弥散系数在非均质多相岩层中的尺度效应［J］.地学前缘，2010，17(3):276-280.(DONG Shuning，DAI Zhenxue，LI Jingsheng.The scale dependence of dispersivity in multi-facies heterogeneous sediments［J］.Earth Science Frontiers，2010，17(3):276-280.(in Chinese))