孔壁通透率对平面附壁射流的影响
龚 升,吴锤结,高 南
(大连理工大学航空航天学院,大连 116024)
0 引 言
流动分离是工程中常见的现象,一些典型的分离流动的动态特性也一直是学者们研究的对象,例如前向台阶[1]、背向台阶[2]、钝头体绕流[3]、管道突扩[4]、腔体[5]以及附壁射流[6]等。这些流动具有一些共同的特点是当流动出现分离以后在流场内形成具有较大速度梯度的区域,大尺度涡旋结构在此区域内产生并发展。这些大尺度结构卷吸分离区内的流体,使分离区内的压强降低。因为低压区的存在,时均流线逐渐向分离区弯曲,并最终贴附在壁面上,在附壁点附近形成局部的高压区。大部分流体在附壁以后向下游流动,而少部分流体向分离区流动,形成回流区[7]。
图1所示的平面附壁射流是一个靠近固体壁面的二维射流,它的出口速度方向平行于壁面。射流靠近壁面一侧形成类似其他分离流动的剪切层和回流区,在射流远离壁面一侧还有另一个剪切层形成并发展。这样的附壁射流在塑料薄膜和造纸等生产过程中常被用来冷却或干燥产品物面。Sawyer[8]、Nasr和Lai[9]、Nozaki[10]、Lund[11]以及Gao和Ewing[12-13]等相继研究了与之相类似的平面附壁射流的流场平均特性。Gao和Ewing通过测量流场平均速度以及脉动压强的相关性发现小偏移距离附壁射流(Hs/Hj≤1)的向下游发展的过程可以分为以下几个不同阶段:在接近射流出口区域(x/Xr≤0.65),射流逐渐改变流动方向,流动方向偏向壁面但最大流动速度不发生变化,这里Xr为再附着区的时均长度。射流在0.65<x/Xr≤1.1范围内贴附在壁面上,射流沿壁面逐渐向下游发展,其速度分布在x/Hj≥6区域内逐步变化,在x/Hj≥10区域内附壁射流的速度分布与普通壁面射流(没有初始偏移Hs=0)完全相似,进入充分发展的壁面射流状态。
以往的研究还发现平面附壁射流附壁点到射流出口壁面之间的回流区的长度(Xr)随着射流距离壁面的高度(Hs)变化而变化。Nasr和Lai[9]研究了Hs/Hj=1~20的射流,发现Xr/Hj随着Hs/Hj增长,他们根据实验结果给出了分离区长度和射流高度之间的关系Xr/Hj~(Hs/Hj)0.851。Gao和E-wing[12]研究偏移高度较小的平面内附壁射流(Hs/Hj≤1.0)时发现,当Hs/Hj≤0.2时,分离区长度Xr/Hs≈6与背向台阶下游回流区长度相似[14]。当0.4≤Hs/Hj≤1时,Xr/Hs逐步减小至4.6。另外,分离区的大小和流动的初始状态,比如来流雷诺数、来流边界层厚度(θ/Hs)等有关[12]。
射流内侧剪切层的大尺度结构会使射流的附壁点随时间发生变化,附壁点附近以及回流区内部的压强也相应发生变化。分离流动参数的亚周期性动态特性也引起了学者们很大的兴趣。Gao和Ewing[12]通过测量流场脉动速度和壁面脉动压强的相关函数研究了附壁射流中的大尺度拟序结构,他们使用的平面射流下沿距壁面高度为1个射流高度,即Hs/Hj=1,发现剪切层内的旋涡结构造成壁面压强发生亚周期性变化,压强的功率谱在特征频率f·Hj/Uj在0.1~0.2范围内均匀分布,没有明显的尖峰存在,他们认为这个频段的脉动压强是分离流场的涡脱不稳定性(shedding instability)引起的。Wee等人[15]和Hudy等人[16]通过线性不稳定性分析和实验方法研究背向台阶流动的涡脱不稳定性,发现该不稳定性特征频率(f·Hj/Uj)约为0.1。他们提出该不稳定性是由向下游传播的涡旋脉动信息与回流向上游传播脉动信息相互作用引起的自激作用造成的(self-sustained oscillations)。除此之外,Gao和Ewing[13]还发现平面附壁射流在分离区内还有一个明显的低频抖动不稳定性(flapping instability,特征频率为f·Hj/Uj<0.04),其长度尺度与分离区长度基本一致,特征频率为涡脱特征频率的若干分之一。当射流贴附在壁面后,在剪切层中生成的旋涡结构对壁面的影响随着距出口的距离增加逐渐减弱。在射流内侧和外侧剪切层生成、发展的旋涡结构配对并融合,融合后的旋涡结构逐渐变大,其形态与没有初始偏移高度的普通平面射流(Hs/Hj=0)非常相似[12-13]。
有的学者尝试通过一系列手段影响附壁射流的发展。Tanaka等人[17-19]通过在一个圆周附壁射流(radial reattaching jet)分离区内抽吸和吹入另一小股恒定流量射流的办法来控制主射流的分离区大小。他们发现分离区内被吹入气体以后,分离区内部压强会有所增加,压强梯度有所减小,分离流动曲率会相应减小,分离区长度相应变长。而从分离区抽吸的流量增加以后,分离区内部压强减小,压强梯度增大,分离流动曲率增大,分离区长度相应变短。使用恒定流量射流的主动控制方法也被Forliti和Strykowski[20]使用在背向台阶流动中,还被Greenblatt[21]等用在控制翼型大迎角条件下的背部分离流动中,他们发现分离区长度随吹吸流量有相似的变化。Heenan和Morrison[22]使用可以调节通透率的孔板作为背向台阶流动的底板。通过这种被动控制的方式,发现背向台阶流动壁面压强的脉动值随着孔板通透率的提高而降低了。他们认为孔板破坏了分离区低频扰动(f·Xr/Uj~0.1)的反馈机制从而降低了涡旋的强度。在本项研究中,以一个平面附壁射流为对象,使用与Heenan和Morrison类似的办法来研究孔板对不同运动形式的影响,探究孔板降低壁面脉动压强的原因。
1 实验设备和方法
该实验台(如图2所示)从左到右由离心式风机、渐扩段、稳定段、收缩段以及实验段构成。渐扩段为木制,其他部分为5mm厚有机玻璃制。在稳定段前后加有孔板进行整流,使射流出口湍流度小于0.5%。整个实验设施宽度均为294mm。收缩段使用5次多项式曲线进行二元收缩,入口高度为300mm,射流出口高度(Hj)为30mm,收缩比为10。射流出口下沿距壁面高度(Hs)为30mm。实验段长500mm,由一个底板和两个高200mm的侧板组成。在底板上距离射流出口360mm以内(x/Hj≤12)均布着半径为3.5mm的圆孔,孔间间距为2mm。圆孔半径仅为射流旋涡特征长度尺度(Hj)的12%左右,孔的形状及排列方式对涡旋的发展影响可以忽略。实验中可以通过在壁面粘贴无痕胶带的方式改变通透率(孔板开孔面积和总面积比,open-area ratio,OAR)。实验选择的通透率为0、10.7%、21.4%和42.8%。

图2 实验台原理图Fig.2 Schematics of the test rig
实验段正中间(z=0)分布着20个松下WM-61B麦克风来测量壁面脉动压强p,前16个麦克间距为半个射流出口高度(Hj/2),后4个间距为Hj。麦克风使用一台红声HS-6020声强校准仪进行标定,该校准仪能够产生频率为1000Hz、声强为94dB的声音信号。所有麦克风产生的信号经过20倍放大后,通过美国国家仪器公司NI-6014数据采集卡和Labview程序同时采集,采样频率为4096Hz,采样时间为150s。更多关于使用麦克风测量壁面脉动压强见文献[12-13,16]。
流动的动态特征可以通过研究壁面脉动压强的功率谱和不同位置脉动压强的互谱获得,x1和x2两点脉动压强的互谱由如下公式计算:
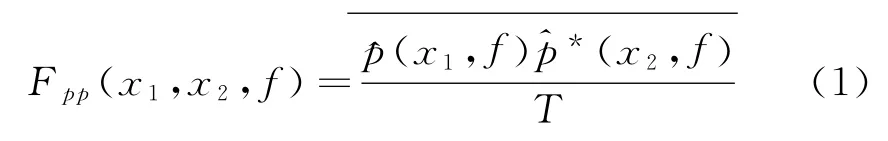
式中^p(x1,f)是壁面压强p(x1,t)的傅里叶变换,*代表共轭,T为采样时间。而互谱的模(相干性系数)由如下公式计算:

互谱的幅角的定义式为:

射流出口速度由安置在稳定段壁面上的一枚压强传感器测量结果算出,传感器测量精度±0.2Pa,测量时间60s,采样频率1024Hz。速度测量精度±0.5%,脉动压强(壁面压强信号的均方根值,p′)测量精度±1%,功率谱和互谱精度为±8%。
采用航华烟线仪进行流场显示实验。一根直径d为0.1mm的304不锈钢丝悬挂在射流出口(x= 0.1 Hj,z=0),钢丝上涂抹石蜡油和柴油的混合液。大容量电容放电加热钢丝上的液滴来产生烟雾并使用一台佳能5DII相机拍摄烟雾。烟线仪使用ATMEGA单片机及人机交互界面对放电电流以及拍照时间进行精确控制。钢丝直径对应的最大雷诺数(Uj·d/υ)为63,基本满足烟线实验对钢丝直径的要求[23]。
2 实验结果与讨论
图3显示的是麦克风阵列测得的不同壁面通透率下壁面压强均方根值的分布,对应射流雷诺数为19000。在附壁过程中,射流内部的大尺度涡旋结构和壁面相互作用,使壁面的压强出现亚周期性的变化。对于全封闭壁面,脉动压强值出现先升高后降低的趋势,脉动压强在附壁点附近(x=4 Hj)达到最大值,最大值幅度与Heenan和Morrison[22]对背向台阶流动的测量结果相近,但比Gao和Ewing[12]测量值低20%左右,峰值出现位置也比Gao和Ewing提前0.5 Hj。这很可能与射流的出口条件有关。本文研究的射流经过5次多项式曲线收缩以后,出口速度形似“礼帽”,流动初始湍流度较小(0.5%),而Gao和Ewing[12]研究的射流是充分发展的流动,射流出口湍流度较大(2.5%)。当壁面通透率为10.7%时,脉动压强的峰值下降大约20%,最大值出现的位置向下游移动至x=5 Hj附近,说明开孔导致平均附壁点向下游移动,分离区的平均长度变长。因为分离区内表压为负值,开孔以后有空气通过孔洞被吸入分离区,导致分离区压强上升,进而使射流附壁过程变得更为缓和,内侧剪切层内的涡旋和壁面相互作用也相应减小,导致壁面脉动压强变化幅度下降。分离区内部压强的脉动强度大幅度降低,说明开孔显著地影响了分离区内部流动,使回流对壁面压强影响减小。随着壁面通透率增加,脉动压强的峰值逐渐下降,最大值出现的位置逐步向下游移动。当通透率为42.8%时,壁面脉动压强逐渐增加,但由射流再附过程产生的壁面脉动压强峰值已不明显。

图3 壁面脉动压强系数分布(Cp′=2p′/ρU2j),射流雷诺数Re为19000Fig.3 Distributions of the fluctuating wall pressure coefficient for jets with a bottom wall of different open area ratios and a Reynolds number of 19000

图4 不同壁面通透率条件下的流场烟线显示图,射流雷诺数Re为7600Fig.4 Visualizations of offset jets with a Reynolds number of 7600 and different open area ratios using smoke wire techniques
图4为雷诺数7600时附壁射流在不同壁面通透率下的流场烟线显示图。应该指出的是,图像显示的每根脉线都是由曾流经电阻丝上某个油滴空气微团的组合,而射流是一个非定常流场,脉线只适于用来指导流场进行初步的定性分析。对全封闭壁面,射流从出口开始向壁面逐渐发生偏移,大尺度涡旋结构在射流两侧剪切层产生,在向下游发展过程中其长度尺度逐渐增大。射流在离开出口以后4~6个台阶高度左右附着在壁面上。由于射流在再附过程中引起的挤压,内侧剪切层内的大尺度涡旋结构在射流附壁以后很快消失,涡旋结构和壁面的相互作用引起了壁面脉动压强的迅速变化,这是时均附壁点附近形成脉动压强峰值的主要原因。当壁面通透率为10.7%的时候,射流出口脉线向壁面偏移角度变小。当壁面通透率进一步增大到21.4%的时候,射流出口脉线几乎平行于壁面发展,“附壁”现象基本消失,射流更趋近于自由发展的平面射流。当壁面通透率为42.8%时,射流为自由平面射流,在射流两侧依次出现旋转方向相反的大尺度涡旋结构,这些结构清晰完整,不受壁面的影响。随着这些结构长度尺度的增加,它们对壁面压强的影响逐步加大,但由附壁作用产生的较强的相互作用已经消失。
为进一步研究壁面开孔对射流动态特征的影响,对壁面压强信号进行傅里叶变换,获得了脉动压强的功率谱以及不同位置脉动压强的互谱。图5所示的是沿流向方向距离射流出口x/Hj为2,4,6和8四个位置的壁面脉动压强的功率谱。对于全封闭底板射流,在接近射流出口位置x/Hj=2和4上,功率谱在0.03≤f·Hj/Uj≤0.3特征频率范围内分布比较平缓,说明此区域脉动压强中存在低频和高频多种运动成分(即低频的摆动flapping和高频的内剪切层涡旋shear layer structures[12]),壁面开孔以后各个频率的脉动压强都有所降低,低频脉动成分(f· Hj/Uj<0.1)降低幅度较大,并且随着通透率的增加而进一步降低。这说明开孔明显削弱了回流区和附壁区内部流动的低频运动组分。
全封闭底板的射流在x/Hj=6开始逐步过渡到类似于普通壁面射流阶段,这一区域的特点是压强的主要脉动频率为f·Hj/Uj=0.07。在x/Hj=6,脉动压强在这一频率上的峰值变得明显,当通透率为10.7%的时候,该峰值略有降低,特征频率也降低为f·Hj/Uj=0.06,说明当射流通过底板开孔卷吸进更多的空气以后,特征频率随着流向速度的降低而有所降低。当通透率进一步增加到超过20%的时候,脉动压强的特征频率为f·Hj/Uj=0.15,这与低通透率有明显的区别,说明这时射流已经变成类似于自由射流的流动,壁面对其动态特性的影响变得微小。
图6所示的是在x/Hj=0.5~8之间各点壁面脉动压强与x1/Hj=2处脉动压强之间互谱在不同频率下的模(相干性系数,γpp)的分布。模的大小反映位置x1与位置x两点的脉动压强在某一特定频率f上的相关性。作为参照信号的p(x1=2 Hj)与其自身的相干性系数在所有频率上均为1,与其他位置p(x≠2 Hj)相干性系数小于1。当使用全封闭壁面时,相干性系数γpp(x1=2 Hj,x,f)在区域x/Hj≤8和特征频率f·Hj/Uj<0.04范围内以及区域x/Hj≤6和特征频率0.2<f·Hj/Uj<0.4范围内有较大的值,说明壁面压强的低频脉动主要集中在前一个区域,而高频的脉动集中在后一个区域,根据Gao和Ewing[12-13]测量结果可推断出这两种运动分别代表着射流的低频摆动和内侧剪切层旋涡运动。当通透率为10.7%时,低频(f·Hj/Uj<0.05)的相干性系数减小,说明低频运动被开孔所削弱,而高频的相干性系数逐渐增大,具有较大相干性系数的区域也得到了扩张,说明具有较高频率的内侧剪切层的旋涡传播区域更长。

图5 壁面脉动压强功率谱,射流雷诺数Re为19000Fig.5 Power spectra of wall pressure fluctuations for offset attaching jets with a Reynolds number of 19000and different open area ratios

图6 不同壁面通透率下壁面脉动压强互谱的模(相干性系数),射流雷诺数Re为19000。壁面通透率0,10.7%,21.4%和42.8%。图中在f·Hj/Uj=0.025和0.24两特征频率上绘制的白线为辅助观察线Fig.6 Cross-spectra of the wall pressure fluctuations measured at x/Hj=0.5to 8and different open area ratios 0,10.7%,21.4%and 42.8%with a Reynolds number of 19000
随着通透率进一步增大到20%以上,相干性系数反映出低频运动已经消失,而由剪切层内旋涡引起的壁面脉动压强相干性更好,传播区域更长,这说明低通透率情况下低频摆动起到了抑制剪切层旋涡传播的作用,通过开孔消除射流的低频摆动,剪切层旋涡变得更容易传播,流动更接近没有壁面影响的平面自由射流。
为了更深入地了解这两种运动形式,对其壁面压强互谱在两个特征频率上(f·Hj/Uj=0.025和0.24)的幅角进行分析,如图7所示。当为全封闭壁面时,在1≤x/Hj<3之间以及x/Hj>5区域的压强低频脉动(f·Hj/Uj=0.025)与x/Hj=2的压强同相,3<x/Hj<5之间的脉动压强与x/Hj=2的压强反相,这说明射流在这个频率上是一个近似上下摆动的运动过程。当空隙率增加到10.7%以后,射流保持了低频摆动特性。但空隙率进一步增加到20%以上之后,低频幅角连续增加,表示摆动已经消失,取而代之的是扰动连续向下传播的运动形式。对不同通透率的流场,高频(f·Hj/Uj=0.24)幅角都是线性增加的,这说明该频率相对应的涡旋以一近似固定的传播速度向下游传播。需要指出的是在1≤x/Hj≤5区域,封闭底板射流幅角斜率要超过其他射流,这说明开孔减弱了涡旋的附壁过程,从而加快了这个区域内涡旋的向下游移动速度。

图7 不同通透率下壁面脉动压强互谱在频率f·Hj/Uj=0.025和0.24的幅角Fig.7 Phase angle of the cross-spectra of the fluctuating wall pressure for the frequencies of f·Hj/Uj=0.025and 0.24with different open area ratios
3 结 论
研究了不同壁面通透率(0、10.7%、21.4%和42.8%)对平面附壁射流动态特性的影响,发现开孔壁面对旋涡的发展有明显的影响。实验结果表明,随着壁面面积通透率的逐步增加,流场中特征频率为f·Hj/Uj<0.04的低频抖动现象逐步消失,流动再附壁面的过程变得更为和缓,剪切层内旋涡和壁面相互作用降低,致使壁面压强的脉动幅度减小。当孔壁通透率超过20%时,射流出口的流线几乎与壁面平行,壁面脉动压强幅度缓步增加,射流的动态特性与平面自由射流非常类似,剪切层内涡旋的传播速度也比附壁射流中的传播速度快。
[1] Camussi R,Felli M,Pereira F,et al.Statistical properties of wall pressure fluctuations over a forward-facing step[J].Physics of Fluids,2008,20(7):075-113.
[2] Eaton J K,Johnston J P.A review of research on subsonic turbulent flow reattachment[J].AIAA Journal,1981,19(9):1093-1100.
[3] Cherry N J,Hillier R,Latour M E M.Unsteady measurements in a separated and reattaching flow[J].Journal of Fluid Mechanics,1984,144:13-46.
[4] Tinney C E,Glauser M N,Eaton E L,et al.Low-dimensional azimuthal characteristics of suddenly expanding axisymmetric flows[J].Journal of Fluid Mechanics,2006,567:141-155.
[5] Rowley C W,Williams D R,Colonius T,et al.Linear models for control of cavity flow oscillations[J].Journal of Fluid Mechanics,2006,547:317-330.
[6] Kim D S,Yoon S H,Lee D H,et al.Flow and heat transfer measurements of a wall attaching offset jet[J].International Journal of Heat and Mass Transfer,1996,39(14):2907-2913.
[7] Simpson R L.Turbulent boundary-layer separation[J].Annual Review of Fluid Mechanics,1989,21(1):205-232.
[8] Sawyer R A.The flow due to a two-dimensional jet issuing parallel to a flat plate[J].Journal Fluid Mechanics,1960,9(4):543-560.
[9] Nasr A,Lai J C S.A turbulent plane offset jet with small offset ratio[J].Experiments in Fluids,1998,24(1):47-57.
[10]Nozaki T,Hatta K,Sato N,et al.Reattachment flow issuing from a finite width nozzle:report 2,effects of initial turbulence intensity[J].Bulletin of JSME,1981,24(188):363-369.
[11]Lund T S.Augmented thrust and mass flow associated with two-dimensional jet reattachment[J].AIAA Journal,1986,24(12):1964-1970.
[12]Gao N,Ewing D.Experimental investigation of planar offset attaching jets with small offset distances[J].Experiments in Fluids,2007,42(6):941-954.
[13]Gao N,Ewing D.On the phase velocities of the motions in an offset attaching planar jet[J].Journal of Turbulence,2008,9(27):1-21.
[14]Eaton J K,Johnston J P.A review of research on subsonic turbulent flow reattachment[J].AIAA Journal,1981,19(9):1093-1100.
[15]Wee D,Yi T,Annaswamy A,et al.Self-sustained oscillations and vortex shedding in backward-facing step flows:Simulation and linear instability analysis[J].Physics of Fluids,2004,16(9):3361-3373.
[16]Hudy L M,Naguib A M,Humphreys Jr W M.Wall-pressurearray measurements beneath a separating/reattaching flow region[J].Physics of Fluids,2003,15(3):706-717.
[17]Tanaka T,Tanaka E,Inque Y.Study on control of radial attaching jet flow(3rd report,flow before reattachment point)[R].Bulletin of JSME 29,2482-2486.1986.
[18]Tanaka T,Tanaka E,Nagai K.Study on control of radial attaching jet flow(1st report,effect of control flow on main jet flow near a nozzle).Bulletin of JSME 29,1135-1140,1986.
[19]Tanaka T,Tanaka E,Nagaya S.Study on control of radial attaching jet flow(2nd report,effect of control flow on pressure distributions).Bulletin of JSME 29,2049-2054,1986.
[20]Forliti D J,Strykowski P J.Controlling turbulence in a rearward-facing step combustor using countercurrent shear[J].Journal of Fluids Engineering,2005,127(3):438-448.
[21]Greenblatt D,Paschal K B,Chungsheng Y,et al.Experimental investigation of separation control part 2:zero mass-flux oscillatory blowing[J].AIAA Journal,2006,44(12):2831-2845.
[22]Heenan A F,Morrison J F.Passive control of pressure fluctuations generated by separated flow[J].AIAA Journal,1998,36(6):1014-1022.
[23]Smits A J,Lim T T.Flow Visualization,Techniques and Examples[M].2000.

