模矢法在厚松散层地表移动参数解算中的应用*

冉 典，吴 捷

(安徽理工大学 测绘学院，安徽 淮南 232001)

0 引言

目前，概率积分法在中国矿区开采沉陷预计中广泛被应用。概率积分法是把岩层看作是一种随机介质，把岩层移动看作是一种服从统计规律的随机过程来研究岩层与地表移动的一种方法［1］。但由于厚松散层下开采具有与一般地质采矿条件不同的沉陷特性，用传统的概率积分法对其预计时，预计结果与实际往往偏差较大。基于此对传统概率积分法预计模型进行理论修正，建立厚松散层条件下开采地表移动预计的概率积分法修正模型。

模矢法是解算无约束极值问题的一种直接解法，对解决高度非线性化目标函数最优解问题非常有效。模矢法具有方便计算机编程和加速向最优点移动性质的优点，分别将该方法运用到地表移动参数的解算和采用任意形状的工作面或者动态条件下的实测数据解算参数中，而且该方法可以应用到所有的预计模型中［2］。

1 模型建立

概率积分法预计精度高，使用方便。国内各个矿区可根据其实际情况选择合理的预计模型，对于一般地质采矿条件下的沉陷预计，概率积分预计模型能够满足工程需要。

1．1 模矢法求参概率积分法预计模型

首先根据下沉预计公式求取部分参数，再利用水平移动公式求取剩余参数。

1．1．1 下沉预计公式

下沉预计公式:

式中:Wmax为充分采动条件下地表最大下沉值，Wmax=mqcosα;m 为煤层的开采厚度;q 为地表下沉系数;α 为煤层倾角;θ 为开采影响传播角;H0为平均开采厚度;H1为下山方向开采厚度;H2为上山方向开采厚度;tanβ 为主要影响角正切值;tanβ1为下山方向主要影响角正切值;tanβ2为上山方向主要影响角正切值;x、y 为地表点在工作面特定坐标系下坐标;L0为工作面走向长;L'0为工作面倾向长;S1为倾向主断面下山方向拐点偏移距;S2为倾向主断面上山方向拐点偏移距;S3为走向主断面左边界拐点偏移距;S4为走向主断面右边界拐点偏移距。

式中:B 为所求参数;W(B)为下沉预计值;W实为地表实测下沉值。

1．1．2 水平移动预计公式

水平移动预计公式:

式中:B 为所求参数;U(B)为水平移动预计值;U实为地表实测水平移动值。

1．2 巨厚松散层下概率积分法预计修正模型

在巨厚松散层下，采用传统概率积分法预计结果与实际存在一定的偏差，这是由于概率积分法预计模型基于随机介质理论，没有考虑上覆岩层的岩性不同［3］。鉴于基岩和松散层沉陷特性不同，把上覆岩层分为基岩和松散层两部分。对于基岩部分，可以采用传统的概率积分法进行预计，由于煤层的开采导致基岩上的下沉为:

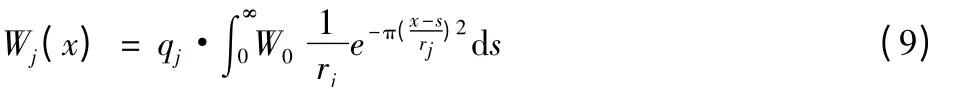
式中:W0为煤层的有效开采深度;qj为基岩上的下沉系数。

按照叠加原理进行地表下沉预计，把基岩面的下沉作为系数对待。地表的下沉可被看成是变采厚煤层的开采引起的，采厚为Wj(x)。根据叠加原理，地表下沉为:

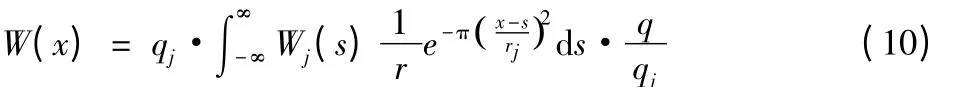
式中:q 为地表下沉系数;r 为开采影响半径，有

式中:φ 为松散层边界角;δ 为煤层的有效开采厚度;tanβ 为主要影响角正切。

对于有限开采的情况，可用叠加原理进行计算［4］。

2 模矢法求取沉陷预计参数

2．1 模矢法的基本原理

模矢法是解算无约束初值的问题的一种直接解法，具有方便计算机编程和加速向最优点移动性质的特点。这种方法的每一次迭代都是交替进行轴向移动和模矢移动。轴向移动的目的是探测下降的有利方向，模矢移动的目的是沿着有利方向加速移动。如果探索进行到某一步长后再得不出新的下降点，此时应缩小步长以进行更精确的搜索，当步长已缩小到某一精度要求仍得不到新的下降点时，停止迭代，将该点作为最终所求的近似最优点［5］。

2．2 沉陷预计参数的求取

利用模矢法解算地表移动参数的基本原理、求参模型以及解算参数的计算步骤，以Visual Basic 6．0 为开发工具，编写模矢法求参程序，计算沉陷预计参数。

2．2．1 求取沉陷预计参数的算法流程

求取沉陷预计参数的算法流程，见图1。

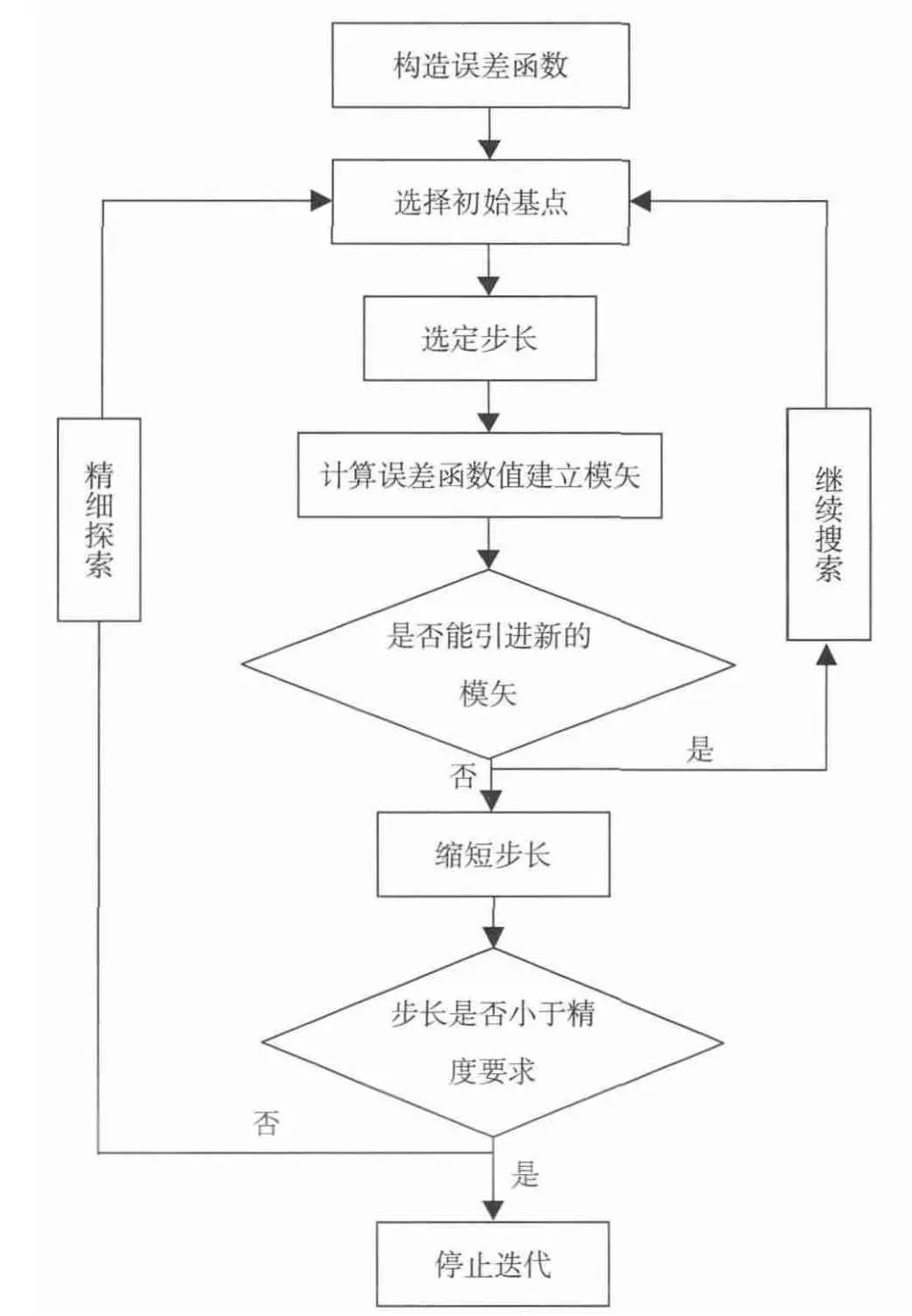
图1 求取沉陷预计参数的算法流程图Fig．1 Algorithm flowchart of calculating estimated parameters

2．2．2 模矢法求参程序流程

在求参过程中，q、tanβ、S、θ 这些参数可通过下沉预计公式求得。剩余的水平移动系数b 由水平移动预计公式求得，以提高参数精度［6］。部分算法流程如下:

第一步，选取初始数据。选取初始点x0，初始步长δ0＞0 ，给定收缩因子α ∈(0，1)，给定允许误差ε ＞0 ，令k = 0 。

第二步，确定参考点。令y = xk，j = 1 。

第三步，进行正轴向探测。从点y 出发，沿ej做正轴向探测:如果f(y +δkej)＜f(y)，令y = y +δkej，转第五步，否则，转第四步。

第四步，进行负轴向探测。从点y 出发，沿ej做负轴向探测:如果f(y －δkej)＜f(y)，令y = y －δkej，转第五步;否则，直接转第五步。

第五步，检验探测次数。如果j ＜n，令j = j +1 ，返回第三步;否则，令xk+1= y，转第六步。

第六步，进行模矢移动。如果f(xk+1)＜fxk，从点xk+1出发沿着加速方向xk+1－xk作模矢移动，令y = 2xk+1－xk，返回第三步;否则，转第七步。

第七步，检查是否满足终止准则。如果δk＜ε，迭代终止，近似最优解为xk;否则，转第八步。

第八步，缩短步长。如果xk+1= xk，令δk+1= αδk，k = k +1 ，返回第二步;否则，令xk+1= xk，δk+1= δk，k = k +1 ，返回第二步。

3 模矢法求参的效果分析

以朱集煤矿首采面(1111(1)工作面)的地表移动观测站的数据为例，采用模矢法解算地表移动参数，对该方法求参进行分析，来验证模矢求参的准确性和有效性。由于朱集矿是已经开展过地表观测的矿山，因此可根据模矢法以及概率积分法参数的经验值(见表1)，来确定1111(1)工作面的地表移动参数，如表2 所示。

根据以上参数，对该首采面地表点下沉值进行计算，并与实测值进行比较。由于朱集矿为巨厚松散层条件下的开采，因此预计模型采用巨厚松散层的概率积分法修正模型进行地表移动变形预计［7］。图2 是概率积分法普通预计曲线和概率积分法修正模型预计曲线与实际观测曲线的对比图，图中曲线经过平滑，从图中可知:概率积分法修正模型预计曲线效果稍好一点，说明修正后的概率积分模型的预计结果更接近实测值。经过统计计算得:

1)该首采面共实测了地表观测站177 个点的下沉值。

2)在这些点中，由预计值与实测值的比较中统计出的最大偏差为79．34 mm，为最大下沉值的9．68%，小于限差15%。

3)预计的残差拟合中误差为M=60．99 mm，为最大下沉值的7．44%，小于残差中误差与最大下沉值之比为10%的限差。

计算分析说明，上述得到的地表移动参数的相应误差都在限差范围内，证明结果是正确的。

表1 地表移动参数初值Tab．1 Initial values of earth's surface movement parameters

表2 地表移动参数计算值Tab．2 Calculating values of earth's surface movement parameters

图2 实测值与预计值对比图Fig．2 Comparison chart of measured and estimated values

4 结论

本文以朱集煤矿为例，对该矿区首采工作面运用模矢法解算地表移动参数，采用巨厚松散层条件下的概率积分的修正模型进行地表移动变形预计，通过与实测数据对比，得出以下结论:

1)模矢法易于编写计算程序，求取参数的过程简单。

2)巨厚松散层沉陷预计，需要对传统概率积分法模型进行修正，以对地表移动进行正确预计。

3)通过预计值与实测值比较分析，证明模矢法理论是正确的。

［1］ 崔有帧． 开采沉陷与建筑物变形监测［M］． 北京:机械工业出版社，2009．

［2］ 谢政，李建平，陈挚．非线性最优化理论与方法［M］． 北京:高等教育出版社，2010．

［3］ 吴侃，葛家新，周鸣，等． 概率积分法预计模型的某些修正［J］． 煤炭学报，1998，23(1):33 -36．

［4］ 煤炭工业部生产司组．煤矿测量手册(下册)［M］．北京:煤炭工业出版社，2001．

［5］ 葛家新．地表沉陷预计参数求取及其分析［J］．矿山压力与顶板管理，2004(1):78 -82．

［6］ 何国清，杨伦，凌赓娣，等． 矿山开采沉陷学［M］． 徐州:中国矿业大学出版社，1991．

［7］ 鄢继选．巨厚松散层条件下地表移动变形动态预报［D］． 淮南:安徽理工大学，2010．