小区域似大地水准面精化的支持向量机技术研究*

谢 波

(重庆水利电力职业技术学院 建筑工程系，重庆402160)

0 引言

似大地水准面是工程技术应用中的正常高Hγ的基准面。随着GPS 定位技术在测量中的应用，利用GPS 定位技术可以测定点的大地高H。正常高和大地高的差值称为高程异常ξ。为实现GPS 技术在真正实用意义上的三维空间测量的功能，似大地水准面的精化实际上就是求解高程异常。似大地水准面精化的方法主要分为:几何解析法和重力法两大类［1，2］。重力法由于对重力数据的分布、精度等要求比较高而有一定的局限性，因而在缺少重力数据的情况下，可以用几何法精化似大地水准面，通过在测区选择一定数量的既有GPS 高程又有精密几何水准高程的控制点，以平面、二次曲面、差值曲面、三次曲面等数学模型加以拟合的方法求定高程异常模型［3，4］。

支持向量机技术［5］基于统计学习理论，目前已成为机器学习研究的热点，成功应用于分类和回归问题。近年来，人们发展了回归支持向量机，它可以按任意精度逼近非线性函数，具有全局极小值点和收敛速度快的优点，被广泛地应用于多个领域。本文将支持向量机技术引入到建立小区域GPS 高程异常模型，编制了基于支持向量回归的二次优化程序，通过试验数据的验证分析，证明了小样本条件下支持向量机模型的拟合精度可靠，在小区域似大地水准面精化中是可行的和有效的。

1 支持向量机的模型和算法

支持向量机的基本思想是通过用内积函数定义的非线性变换将输入空间映射到一个高维的特征空间，在高维的特征空间中寻找输入变量和输出变量之间的一种非线性关系［6］。若选择的K 个数据样本集为(x1，y1)，(x2，y2)，…，(xk，yk)∈Rn×R1，则基于支持向量机的目标函数为:

式中:ω 为权向量;b 为偏差;Φ(·)为把输入空间映射到一个高维特征空间中的非线性映射函数。Φ(·)可以用核函数来代替，即:

核函数可以用原空间中的函数来实现，无需知道Φ(·)的具体形式，因此非线性问题的支持向量机模型为:

式中:(ai- a*i )为非零的支持向量的系数。根据支持向量机回归函数的性质，只有少数(ai- a*i )不为零，这些参数对应的向量称为支持向量，支持向量机模型y(x)完全由其决定。

目标函数中最优的权向量ω 和偏差b 可以通过最小化由拟合误差的平方和及正则化项组成的目标函数［7］得到:

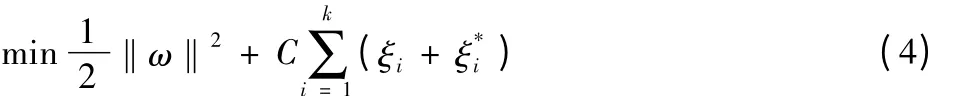
约束为:

式中:ξi，ξ*i 为引入的松弛变量;C 为调节常数，它能够使训练误差和模型复杂度之间取一个折衷以便使所求得的函数具有较好的泛化能力，而且C 值越大，模型的预测误差越小。目标函数的对偶形式为:

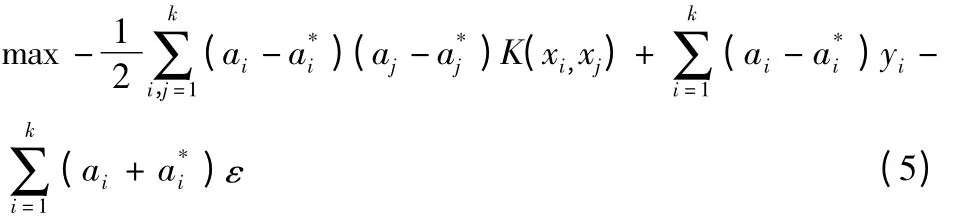
约束为:

解算上述优化方程可以应用数学软件的二次规划工具箱，求得支持向量的个数及系数(ai-a*i)。

核函数K(xi，xj)为满足Mercer 定理的任意连续对称的函数，其中常用的核函数有d 次多项式核函数、径向基核函数、神经网络核函数［8］等。

2 应用实例

为研究支持向量机技术在小区域似大地水准面中的应用，现以某校新校区建设工程为例。该工程测区范围首级施测D级GPS 平面控制点，加密平面控制采用一级导线，参与实验的数据高程点全部施测精密二等水准。数据建模时选取GPS 平面控制测量点SD01、SD05、A ～G 为学习样本，利用中海达V8 GNSS 接收机按D 级精度观测和利用随机平差软件HDS2003 解算各点的三维地方坐标(x，y，H)，同时用Trimble DINI12 施测各点的二等水准。支持向量机模型的输入向量为平面坐标(x，y)，输出变量为高程异常ξ，经过学习训练，得到(ai-a*i )及b，从而建立支持向量模型y(x)。检验样本选取控制点范围内的利用TOPCON GPT-3000LNC 放样的建构筑物的特征点共10个，同时用Trimble DINI12 施测放样点的二等水准，从而计算模型拟合值及精度。

2．1 数据预处理

为避免各个因子之间的量级差异，消除各个因子由于量纲和单位不同造成的影响，建模前首先对每个预报因子分别进行归一化处理，公式为:

式中:Z'i为归一化变量;Zi为原始变量，Zmax和Zmin分别为样本集的最大值和最小值。

2．2 结果及分析

本文选择核函数K(Xi，Xj)= exp(-‖Xi-Xj‖2/γ2)。根据训练样本得到正则化参数C = 1．590 0;取噪声水平σ =0．005 0，则ε=0．007 2。同时，通过不同的核参数寻优的试验得到γ2=0．25。经过学习训练，得到8 个支持向量，各个支持向量的ai-a*i 及其对应的样本序号见表1，相应的b 为0．478 6。

表1 训练样本学习后得到的支持向量及其ai -a*i 值Tab． 1 The support vector and its value ai - a*i after study by training samples

由于实验区域小、数据量少，本文采用平均误差作为支持向量回归的算法的性能评价指标:

式中:K 为样本数:Δi为差值。

表2 列出了用支持向量计算的训练样本和检验样本的数据，图1 显示了训练样本和检验样本的实际值和拟合值的比较。从图1 和表2 可见:训练样本的拟合误差小于0．020 m，平均误差为0．011 m;检验样本的拟合误差除个别点(B2)外均不大于0．030 m，平均误差为0．019 m，总体样本的平均误差为0．015 m，说明了基于支持向量机技术的GPS 高程异常模型的拟合(预测)值与实际值吻合的较好，精度较高，较好的反映了高程异常的变化，即使在小样本时仍十分有效的，显示了该技术的较强的泛化能力。

表2 支持向量机模型的数据Tab．2 Values of support vector machine model

3 结论

支持向量机技术具有学习能力强、泛化能力好、对样本依赖程度低、模型参数确定等优点，尤其在处理较强非线性映射的能力方面优点突出。本文应用支持向量机技术，能较好地模拟GPS 高程异常的变化，研究结果表明该技术无论在历史样本拟合的精度上还是模型的实际预测能力上都具有较高的精度，能满足工程建设的需要。

图1 支持向量机模型比较图Fig．1 Comparison chart of support vector machine models

［1］ 魏子卿．GPS 重力位水准［J］． 大地测量与地球动力学，2007，27(4):1 -7．

［2］ 高伟，卢秀山．GPS 高程区域似大地水准面的分区拟合与平滑连接［J］．测绘通报，2000(7):11 -13．

［3］ 周忠谟，易杰军，周琪．GPS 卫星测量原理与应用［M］．北京:测绘出版社，1997．

［4］ 华锡生，黄腾．精密工程测量技术及应用［M］． 南京:河海大学出版社，2002．

［5］ Vladimir N．Vapnik．统计学习理论的本质［M］． 张学工，译． 北京:清华大学出版社，2000．

［6］ 吴今培，孙德山．现代数据分析［M］．北京:机械工业出版社，2006:67 ～74．

［7］ 苏高利，邓芳萍．关于支持向量回归机的模型选择［J］．科技通报，2006，3(22):154 ～158．

［8］ 崔万照，朱长纯，保文星，等． 最小二乘小波支持向量机在非线性系统辨识中的应用［J］． 西安交通大学学报，2004，38(6):563-565．