直九型直升机基准桨叶共锥度校准技术研究

董海峰

(中航工业哈尔滨飞机工业集团有限责任公司计量中心，黑龙江哈尔滨150066)

0 引言

直升机基准桨叶是生产、调试、检测装配直升机桨叶的比对标准，是直九型直升机桨叶特性参数的参照基准，是直升机研发过程的重要部件。桨叶的旋转带动直升机实现垂直起飞、前进及悬停等各种飞行状态，而桨叶的特性参数的准确性则直接影响直升机飞行的品质［1-3］。在制造过程中和装配飞机前，要对直升机桨叶的静态特性参数进行测试，在动平衡试验台上利用基准桨叶对机载桨叶的动态特性参数(共锥度参数)进行校准。共锥度参数是基准桨叶特性参数中最主要的参数之一，对其校准也是基准桨叶校准过程中的重点，又是难点，因此基准桨叶共锥度特性参数的校准尤为重要。

直九机型基准桨叶在上世纪80年代随直九型直升机从法国引进，法国军方一直对直九机型基准桨叶的校准技术进行封锁，因此30年来基准桨叶的共锥度特性参数的准确性处于未知状态。基准桨叶共锥度特性参数的校准技术的研究也日趋紧迫。

1 桨叶共锥度的定义

在工程上，通过被测桨叶的锥度与标准桨叶锥度的差来表述被测桨叶的共锥度的特性。由于在实际工程上，直接测量两片桨叶的锥度差比较困难，通常用两片桨叶挥舞高度的相对差值来表示共锥度。用这一参数来表征桨叶挥舞轨迹一致性的程度［4-5］。如图1。

h1，h2，h3，hB1分别为三片桨叶在不同锥度下的挥舞高度，通过测时法实现桨叶共锥度的测量。

2 直九型基准桨叶共锥度参数校准装置的测量原理

基准桨叶共锥度参数校准装置如图1所示，其测量原理是利用三组激光束，使旋转状态下的三片桨叶按顺时针切割激光束，通过测量时序脉冲信号和时序算法程序计算出基准桨叶的共锥度参数。

图1 基准桨叶共锥度参数值实际分析原理图

在使用激光测量方法的过程中，由于桨叶在切割两束激光交叉区域时，激光束很短，桨叶切割两束激光的时间间隔很短，要求信号处理系统的采集频率高，噪声小。因此，这里的信号采集芯片采用的是美国德州仪器公司的CPLD(高速逻辑信号阵列)和DSP(高速信号处理器)，通过采集和处理三片桨叶的脉冲信号，并对算法程序进行非线性补偿，从而获得共锥度参数。

2.1 校准装置的采样频率

由于未引入非线性补偿时，将基准桨叶共锥度参数校准装置的不确定度理论设定值为5 mm，因此本文主要基于测量过程的逆向过程，将基准桨叶共锥度参数校准装置的分辨能力设定为0.2 mm 左右。这也就是说，当两片桨叶的高度差小于或等于0.2 mm 时，校准装置会将这两片桨叶视为挥舞高度相同的桨叶。因而，一片基准桨叶在激光束中穿过时，如果它的波动介于±0.2 mm 区间，系统是测量不出来时间差的。

那么，当两片桨叶挥舞高度方向出现0.2 mm 差值，设桨叶在水平方向上运行的距离为x(见图2)，由此可计算出系统的采用频率。具体地，根据公式

有

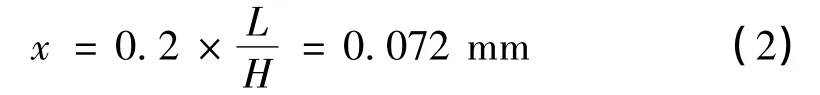
设定基准桨叶半径R 所取的最大整数为6000 mm，旋翼转速n 为366 r/min，则

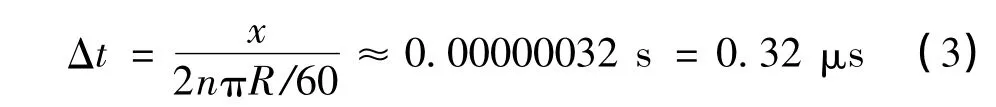
从而采样频率f=3 MHz。而基于采样定理，真实的采样频率应为计算频率的2 至3 倍，因此校准装置的采样频率应为10 MHz。

2.2 测量算法非线性补偿原理

实际应用中，桨叶上的旋翼锥体与激光平面相切所产生的三个切点并不是在同一条直线上，而是在两个平面的相贯线上(图1 和图2 中的虚线为相贯线)。相贯线为桨叶理论上的挥舞轨迹(即桨叶没有弯曲的情况下的轨迹)。

理论分析的算法中采用的是桨叶扫过B 和C 点的时间差ΔtBC，但在实际测量过程中，这一差值是很难被测得的;通过测量时间序列，得到激光平面与桨叶的挥舞轨迹锥体的相贯线上B1与C 间的时间差值ΔtB1C。显然，二者间的高度差为BB1。激光信号时序图见图3，且该差值随着桨叶挥起的角度不同呈非线性变化。

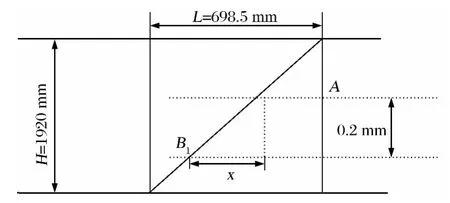
图2 基准桨叶共锥度参数值理论分析原理图

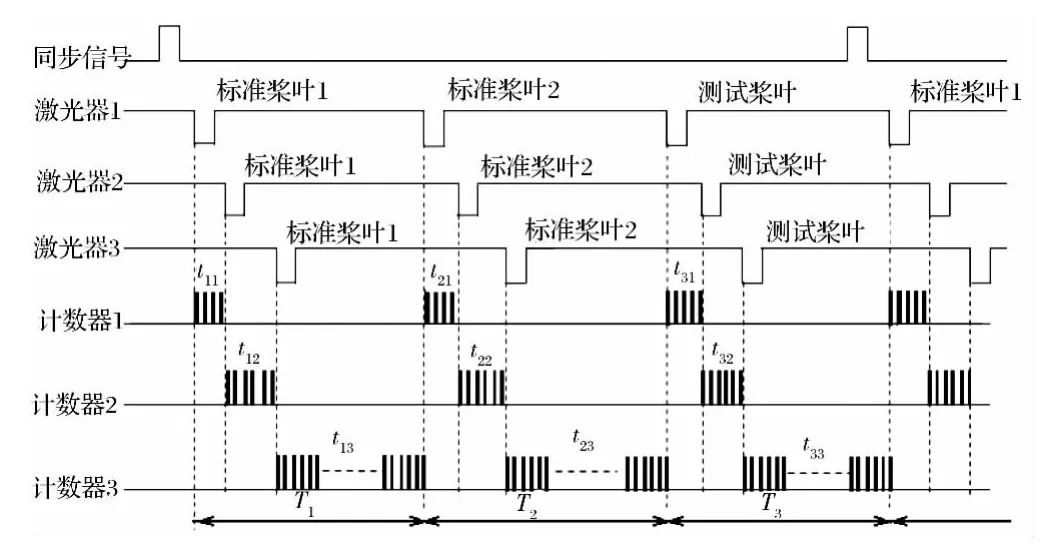
图3 激光信号时序图

通过估算，桨叶挥起的高度约为500 mm，桨叶挥舞参数测量点半径约5556 m。则桨叶挥舞锥度角β=arcsin(500/5556)=5°。两束垂直激光器的距离为700 mm，不经过算法修正，则由抛物线引起的最大误差为-0.9 mm，由桨叶挥起角度引起的非线性误差已经超出了系统要求的误差范围，必须进行非线性的修正。

桨叶挥舞参数校准系统激光器结构如图4所示，其中，O 是旋翼的桨毂中心，FⅠ和TD 是两个垂直激光器，L 是二者安装距离，与桨毂中心水平夹角为α，ⅠT 为斜激光器，θ 为倾斜角度，三者形成一个激光平面;并且，OEG 是桨毂平面，桨叶挥舞呈倒锥体，AKC 是桨尖的轨迹平面，桨叶OK 切割三束激光的切割点为A，B1，C 三点。由于L 约为700 mm，相比于桨叶桨尖的旋转周长2πR(约为35000 mm)是一个相对小的量，因此可以认为在这个过程中桨叶的挥舞角度为定值。H 是桨叶挥舞高度，h0是靠近地面的激光束交点离桨毂平面的距离，h 为桨叶测量靶点的挥舞高度，桨叶挥起的角度为β。

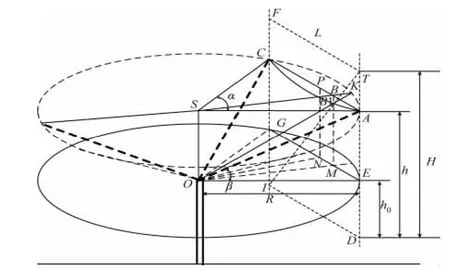
图4 激光器空间安装结构图

在图4 中，ON 为O 点到EG 的垂线，可知

已知

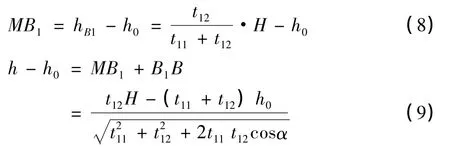
以上是以桨盘平面为参考的桨叶挥起高度，则3片基准桨叶的挥舞高度h1，h2，h3分别为

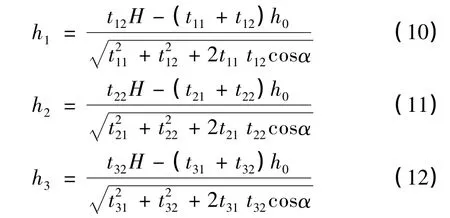
三片基准桨叶间的挥舞高度差为

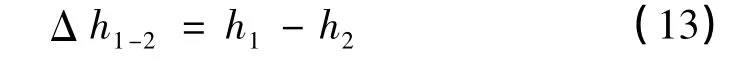
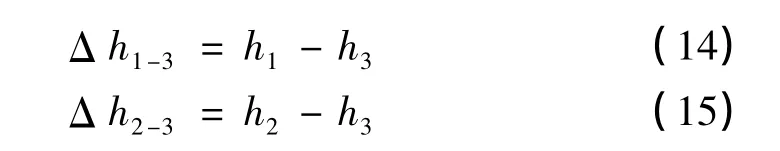
该算法考虑了桨叶挥起角度本身和三组激光器安装参数对挥舞高度的非线性影响，很好地补充了基准桨叶在大桨距状态动平衡试验时挥舞参数的误差。

3 直九型基准桨叶共锥度参数校准装置的标定

3.1 标定方法

要确保直九型基准桨叶共锥度参数校准装置的准确性，就必须对其进行校准，使其能够计量溯源，据此本文研究的校准技术中设计了一套标定系统。当桨叶有挥舞角度时，切割激光会产生抛物线误差，而当桨叶与激光平面垂直时，则不会产生测量误差。因此，本文使用有一定高度差的刚性模拟桨叶切割三束激光，并使刚性模拟桨叶与激光平面垂直，以固定的转速使刚性模拟桨叶切割激光束信号，从而利用刚性模拟桨叶间的固定高度差值校准直九型基准桨叶共锥度参数校准装置。该方法可以溯源到标准量块(几何量标准)，其溯源过程见图5。

图5 校准溯源图

3.2 标定系统结构

每两片模拟桨叶的高度差为100 mm，由精密转台驱动旋转，精密转台安装在升降台上，升降台的调整范围为0 ～1500 mm，可保证激光器在0 ～1000 mm 的测量范围内任意位置切割激光束，这个测量范围即是基准桨叶共锥度参数校准装置的最大测量范围。桨叶的仿真模型和标定系统结构图分别见图6 和图7，实际安装结构如图8所示。

4 校准装置不确定度分析及验证

4.1 B 类不确定度评估分析

1)基准桨叶挥起角度β 的最大值约为7°，测量靶点的半径是5786 mm，则桨叶的挥舞高度是710.4 mm。若采用非线性补偿算法，那么测量误差的最大值为a1=0.5 mm，服从均匀分布，，其带来的不确定度为u1=0.28 mm。

2)基准桨叶安装引入的误差a2=0.1 mm，服从均匀分布，，其带来的不确定度为u2=0.056 mm。

3)环境阵风对基准桨叶挥舞参数的影响误差a3=2.0 mm，误差区间半宽度为1.0 mm，服从均匀分布，，其带来的不确定度为u3=0.57 mm。

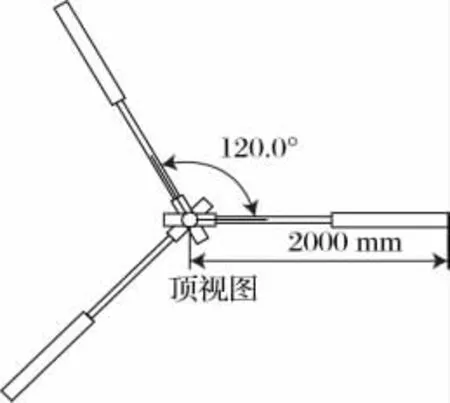
图6 仿真桨叶俯视图

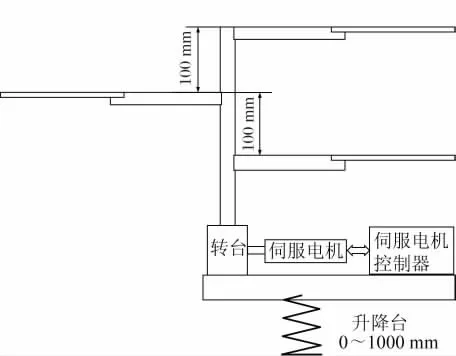
图7 标定系统结构图

图8 转台、升降机构及模拟桨叶实际安装结构

4)动平衡试验台转速引入的误差a4=0.1 mm，均匀分布，，其带来的不确定度为u4=0.056 mm。

以上B 类综合不确定度为

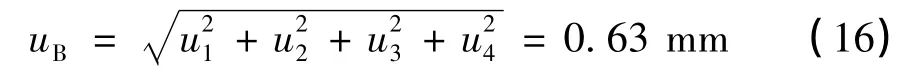
4.2 A 类不确定度的评估分析

使用基准桨叶共锥度参数校准装置测量基准桨叶的共锥度参数，动平衡试验台转速为360 r/min，共进行10 次测量，测量结果分别为:1.1，-0.5，0.3，1，-0.6，-0.3，-0.5，-0.9，-0.4，-0.8 mm。

由贝塞尔公式，n 次独立测量的试验标准偏差为

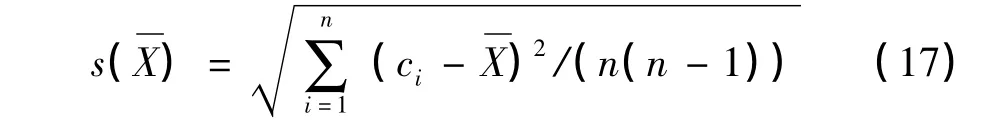
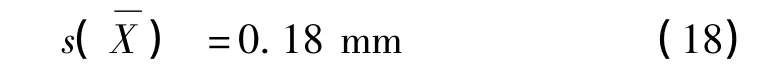
从而uA=0.18 mm，合成标准不确定度为

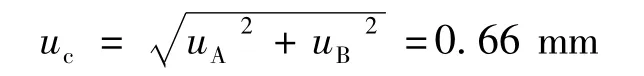
取包含因子k=2，因此，扩展不确定度为

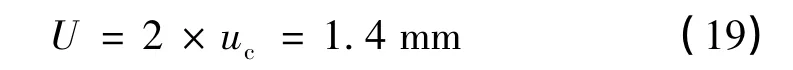
由不确定度评定结果可知，经过非线性补偿设计后，基准桨叶共锥度参数校准装置的不确定度为1.4 mm，小于没有引进非线性补偿前的理论值(5 mm)，说明该方法可以满足直九型直升机基准桨叶共锥度校准及测量的要求。

5 结论

本文研究了现有直九型直升机基准桨叶校准装置的测量原理，分析了传统测量方法，并通过算法程序对该测量方法进行了非线性补偿分析，使其共锥度测量结果更加准确可靠;其次建立了直九型基准桨叶共锥度参数校准装置标定系统，从而对激光器定位参数进行标定。进入现场后，通过这套系统实现了基准桨叶挥舞参数的校准和溯源。所研究直九型直升机基准桨叶共锥度参数的校准技术，可以推广到其他机型直升机桨叶的校准上。

［1］Wilby P G.The development of rotor airfoil testing in the UK［J］.

Journal of the American Helicopter Society，2001，46:210-220.

［2］Kyung-SuNa，Ji-Hwan Kirn.Dynamic Analysis for the Deployment of a Multi-Link Flexible Structure Undergoing Locking［J］.AIAA，A01-25215，2001.

［3］Yihua C，Yong C，Kungang Y，et al.Nonlinear Inverse Dynamics Control of the Aircraft in the Presence of Windshear［J］.Aircraft Engineering and Aerospace Technology，2004，76:592-599.

［4］Haowen W，Zheng G，Zhaochang Z.Aero-elastic response and stability of helicopter rotor blades in forward flight［J］.Journal of Vibration Engineering，1999，12(4):521-528.

［5］He C J，Lewis W D.A Parameters Study of Real Time Mathematical Modeling Incorporating Dynamic Wake and Elastic Blades［C］// AHS 48th Annual Forum.Washington，DC:AHS，1992:1181-1196.