汽轮机转子温度计算中惯性环节系数的确定方法
杨 宇
(上海发电设备成套设计研究院,上海 200240)
汽轮机在启动、停机和负荷变动时,转子的外表面温度随蒸汽温度的变化而剧烈变化.由于热阻和热容的存在,转子内部的温度变化相对较慢,转子外表面和转子体积平均温度之间的温差较大.该温差越大,外表面的热应力就越大,转子的寿命损耗也越大.通过监控转子外表面和转子体积平均温度之间的温差,可以监控转子外表面的热应力.
由于转子是连续旋转的,无法通过安装测温元件来直接测量其温度,需要采用计算方法来获得转子的温度分布.根据非稳态传热原理,转子的热传递可采用经典控制理论中的惯性环节来模拟.工程上,仅采用一个惯性环节无法完成模拟,需采用3个以上并联的惯性环节才能达到要求.目前,针对多个并联惯性环节的时间常数和权重系数的确定,还没有合适的方法[1-2].
笔者介绍了一种将汽轮机转子有限元温度场计算得到的体积平均温度作为标准值,采用基于模式的直接搜索算法来确定并联惯性环节的个数,以及每个惯性环节时间常数和权重系数的方法.
通过Matlab软件自带的基于模式的直接搜索工具箱中的搜索函数来完成优化搜索,不需要编制复杂的优化算法,就可通过离线有限元计算所得的体积平均温度来确定惯性环节的个数、时间常数和权重系数,且获得的优化结果可通过与其他工作条件(启动、停机和负荷变动)下的温度变化进行对比来验证其适用性.
1 惯性环节法计算转子温度
1.1 转子外表面温度T a
在热应力监控系统中,可利用相应部位的内缸内壁温度代替转子外表面温度.
1.2 转子体积平均温度T m
根据文献[1],将公式按计算逻辑图方式表示(见图1).由于1个惯性环节只有1个待定参数,灵活性不够,而多个惯性环节并联使用能更好地模拟转子的传热过程.在汽轮机热应力监控中,出于在保证精度的前提下计算尽量简捷的考虑,采用3个不同权重系数的一阶惯性环节(PT1)并联来仿真计算转子体积平均温度Tm.其中k1、k2、k3分别为第一、第二和第三惯性环节的权重系数 (3个并联惯性环节的权重系数之和等于1);E2、E3分别为第二、第三惯性环节时间常数的比例系数.转子外表面温度Ta和惯性时间常数T为输入量,转子体积平均温度Tm为输出量.
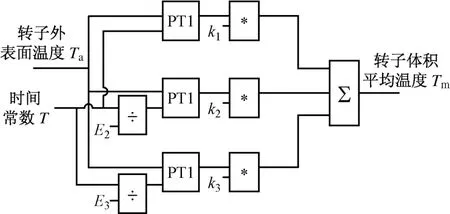
图1 转子体积平均温度仿真计算逻辑图Fig.1 Logic diagram for calculation of bulk temperature
计算汽轮机转子内部的温度分布时,惯性环节法与有限差分法具有相同的精度,但其公式简单,便于编程实现和工程应用.但到目前为止,惯性环节法中的各个系数尚不能采用理论公式计算确定.如何获得符合汽轮机实际运行条件的惯性环节的系数成为工程中应用惯性环节法亟待解决的问题.
2 模式搜索法
模式搜索法作为一种解决最优化问题的直接搜索方法,因为在计算时不需要目标函数的导数,所以在解决不可导或者求导异常麻烦的问题时比较有效.模式搜索法的主要步骤包括轴向探测和模式移动,通过轴向探测找到目标函数下降的有利方向,利用模式移动沿着有利方向加速搜索.
随着模式搜索法的发展,采用变步长搜索策略使得模式搜索方向更接近最优下降方向.而进一步采用插值和非单调技术,不仅改善了方法的局部寻优能力,而且改善了方法的收敛性.
现在已有不少软件将模式搜索算法集成到程序中,如Matlab已经将其添加到工具箱中.使用时只需调用相应的函数,就可以用模式搜索法解决工程问题,大大提高了工作效率,降低了编程工作量[3].
在Matlab程序中通过调用patternsearch函数来进行模式搜索,完整格式为:

其中:v和x分别为取得的最优值及所在的点;@objfun为目标函数objfun的句柄;options为对搜索方式的设置;x0为模式搜索算法的起始点;A、B、Aeq、Beq、Lb和Ub为对x取值的限制条件,具体关系式为

若没有限制则可以设为空,即[].
options采用psoptimset函数设置,完整格式为
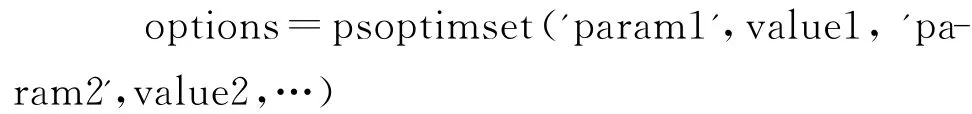
其中:param1、param2为要设定参数的名称;value1、value2为要设定参数的值.
3 惯性环节系数的确定方法
采用图2的流程来确定并验证惯性环节法的时间常数和权重系数.
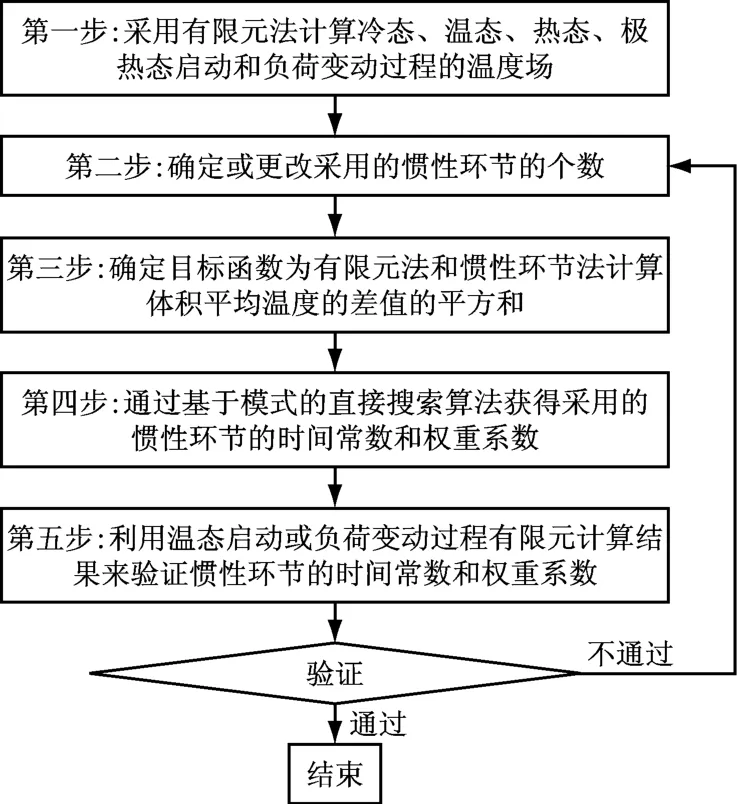
图2 惯性环节系数确定方法的流程图Fig.2 Flow diagram for determination of inertia coefficient
3.1 计算转子温度场分布
对汽轮机转子采用2维轴对称模型,利用有限元软件分别计算冷态、温态、热态和极热态启动过程的温度场变化[4-5].冷态、热态和极热态启动过程中,汽轮机转子的体积平均温度随时间变化的计算结果见表1.表1中的数据将用于确定惯性环节法的时间常数和权重系数.

表1 冷态、热态和极热态启动过程转子体积平均温度Tab.1 Rotor bulk temperature in cold,hot and extremely hot start process
3.2 确定优化搜索的目标函数
要获得惯性环节的时间常数和权重系数,需要先确定目标函数.目标函数就是为完成目标而编写的一个要获得函数值最小化的函数.通过不断调整时间常数和权重系数,搜索目标函数的最小值,完成搜索目标.有限元方法计算所得体积平均温度和惯性环节法计算所得体积平均温度的差值的平方和就是一个可用的目标函数.
需要通过搜索确定的变量有7个:A3、A2、A1、E2、E3、k2和k3.以这7个变量作为目标函数的输入参数,在目标函数中,根据惯性环节的迭代计算公式编写惯性环节输入输出关系.

根据式(2)即可通过前一次的输出值yn-1和本次的输入值xn,近似计算出本次的输出值yn.其中,τa为两次计算的时间间隔.
目标函数关系式为
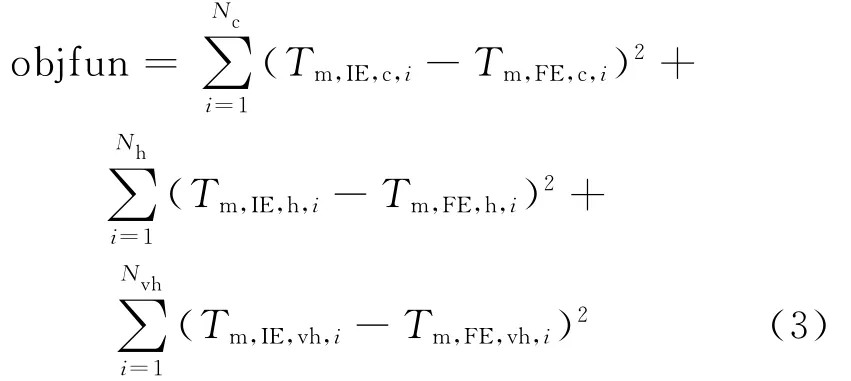
式中:Nc、Nh和Nvh分别为冷态启动、热态启动和极热态启动 的 关 键 时 间 点 的 数 量;Tm,IE,c,i、Tm,IE,h,i和Tm,IE,vh,i分别为惯性环节法计算所得冷态启动、热态启动和极热态启动的关键时间点的转子体积平均温度;Tm,FE,c,i、Tm,FE,h,i和 Tm,FE,vh,i分 别 为 有 限 元 法 计算所得冷态启动、热态启动和极热态启动的关键时间点的转子体积平均温度.
即顺序计算利用惯性环节法所得冷态、热态和极热态启动过程的转子体积平均温度和对应有限元法计算所得的转子体积平均温度的差值的平方和,并以累积值作为目标函数的输出值.
3.3 获得惯性环节的时间常数和权重系数
在Matlab软件的命令行输入下面的语句,完成有约束问题的模式搜索:

其中:options是利用psoptimset函数创建的参数结构;[50 000,-20,-0.5,50.0,50.0,0.3,0.3]为各搜索系数的初始点;[20 000.0,-50.0,-1.0,1.0,1.0,0.0,0.0]为各搜索系数的下限值;[100 000,1.0,0.0,100.0,100.0,1.0,1.0]为各搜索系数的上限值.
初始目标函数值为1 486 920;1 000次迭代计算后,目标函数值为427.68;2 000次迭代计算后,目标函数值为85.03;3 000次迭代计算后,目标函数值为45.27;4 000次迭代计算后,目标函数值为37.72.
获得的优化搜索系数为:
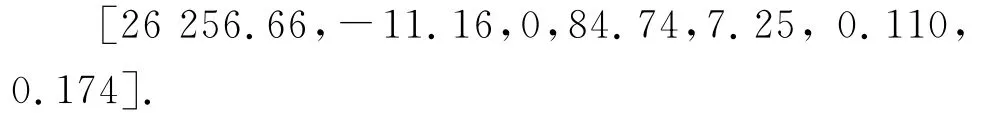
通过优化搜索得到7个变量的值分别为:A3=26 256.66;A2=-11.16;A1=0;E2=84.74;E3=7.25;k2=0.110;k3=0.174.
3.4 验证惯性环节的时间常数和权重系数
对冷态、热态和极热态启动工况完成搜索后,还需要利用温态启动、停机和负荷变动等工况的数据进行验证.利用3.3节获得的惯性环节的时间常数和权重系数,采用惯性环节法计算得到温态启动的汽轮机转子体积平均温度(如表2所示).同时,在表2中列入有限元软件计算所得的温态启动过程中汽轮机转子体积平均温度随时间的变化结果,表2中的数据将用于验证惯性环节法的时间常数和权重系数.如果两者温度差值较大,可调整惯性环节的个数,重新从3.2节开始计算.表2中两者的温度差值不超过1.0 K,表明3.3节获得的时间常数和权重系数满足工程应用的精度要求.

表2 温态启动过程转子体积平均温度的比较Tab.2 Comparison of rotor bulk temperature in warm start process
4 结束语
(1)采用模式搜索法克服了现有技术的不足,利用离线有限元计算所得转子体积平均温度可确定惯性环节的个数、时间常数和权重系数,从而解决了惯性环节法工程应用的技术难题.
(2)采用惯性环节法计算所得的汽轮机转子体积平均温度与有限元软件计算所得的汽轮机转子体积平均温度的差值不超过1.0 K,满足工程应用的精度要求,可提高在线实时监控系统中转子体积平均温度与转子表面的温差及热应力计算的准确性,为汽轮机转子的热应力优化控制和汽轮机变负荷运行的安全性提供技术保障.
(3)模式搜索法虽然能满足全局寻优的要求,但其迭代次数多、运算时间较长、效率不高,后续尚需开展相关研究,采用其他优化算法来设法提高寻优效率.
[1] 杨宇,祁昊,邓志成,等.基于惯性环节的汽轮机转子温度计算方法[J].动力工程学报,2013,33(8):586-590.YANG Yu,QI Hao,DENG Zhicheng,et al.Calculation of turbine rotor temperature based on inertial element[J].Journal of Chinese Society of Power Engineering,2013,33(8):586-590.
[2] 刘岩,杨宇,陈钢.1 000 MW汽轮机高压转子温度在线仿真计算方法的研究[J].发电设备,2012,26(5):21-24.LIU Yan,YANG Yu,CHEN Gang.On-line simulation and calculation on high-pressure roter temperature of a 1 000 MW steam turbine[J].Power Equipment,2012,26(5):21-24.
[3] 雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005:208-258.
[4] 李维特,黄保海,毕仲波.热应力理论分析及应用[M].北京:中国电力出版社,2004.
[5] 史进渊,杨宇,邓志成,等.大功率电站汽轮机寿命预测与可靠性设计[M].北京:中国电力出版社,2011.

