地震作用下挡土墙抗滑动稳定性的拟动力分析

黄睿，夏唐代，钟丽娜，陈炜昀

(1. 浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州，310058；2. 中国联合工程公司，浙江 杭州，310022；3. 南京工业大学 交通学院，江苏 南京，210009)

自2008 年四川汶川发生罕见的8.0 级地震以来，我国的土木工程行业规范对抗震设计提出了更高的要求。重力式挡土墙作为一种经济适用的支护结构，在我国各类基建工程中有着广泛的应用，但是，对其抗震设计的理论研究却并不成熟，因此，有必要开展系列而深入的研究工作，为挡土墙的抗震设计提供参考。目前，对于挡土墙的抗震设计，运用最广泛的理论是由Okabe 和Mononobe 提出的拟静力法。该方法是基于库仑土压力理论，将地震作用力看作是作用于滑动土楔体的惯性力，再根据楔体受力平衡条件得到土压力的计算公式。Morrison 等[1]利用此方法，假设土体滑裂面为对数螺旋线或者对数螺旋线和直线的组合，取得了一系列研究成果。Richards 等[2-3]在Mononobe-Okabe 理论的基础上，改进得到计算黏性土的地震土压力公式。然而，拟静力法假设墙后的填土是刚体，且地震加速度不随时间发生变化，也无法考虑地震波的相位影响，这些都与实际情况不符。针对以上问题，Steedman 等[4]提出拟动力法，假定地震加速度沿挡土墙底以正弦形式向上传播，传播速度为地震波速，这样就考虑了地震波传播的时间和相位差对惯性力的影响。Zeng 等[5]通过离心机试验验证了拟动力法的合理性。基于拟动力法分析的思路，Choudhury 等[6-9]考虑墙背面竖直、填土面水平的挡土墙工况，对地震作用下墙后填土的主动、被动土压力进行研究，并分析了临水挡土墙的稳定性；Ghosh 等[10-11]计算分析了墙背面倾斜和折现型挡土墙的地震土压力；王志凯等[12-13]考虑地震加速度的放大效应和墙面倾角，推导出改进后的土压力计算公式，并指出放大效应对地震土压力的分布有显著影响；马少俊等[14-15]针对忽略地震加速度放大效应和填土面水平的情况，分析讨论了地震作用下挡土墙的稳定性。本文作者基于拟动力法的基本思路，以重力式挡土墙为研究对象，考虑地震加速度放大效应、墙背面倾角、填土面倾角的影响，对地震作用下的抗滑动稳定问题进行建模分析，参考国家地基规范的定义，提出抗滑动安全系数的计算方法，并通过数值算例，分析讨论地震放大效应、地震加速度影响系数、填土内摩擦角、墙土间外摩擦角、墙背面倾角和填土面倾角对挡土墙抗滑动稳定性的影响；再将计算结果与Mononobe- Okabe 方法进行对比，分析两者的异同。

1 理论模型

1.1 基本假定

本文采用拟动力法，针对模型提出以下假定：

1) 挡土墙受力简化为平面应变问题，不考虑挡土墙尺寸等空间效应。

2) 墙后土体处于极限平衡状态时，形成滑动楔体，2 条滑动面通过挡土墙墙蹱，1 条沿着墙背，另一条位于后方填土内，不考虑挡土墙破坏模式。

3) 墙后填土为均质且各向同性的无黏性土。

4) 墙后填土和挡土墙的剪切模量(Gs和Gw)为常数。

5) 地震加速度随时间和深度变化，且水平、竖向地震加速度分别与相应材料中的地震剪切波、压缩波波速有关。

6) 地震加速度峰值从墙底基础沿挡土墙高度线性增大。

7) 地震时，填土和挡土墙下部基础的土体以正弦的稳态形式振动。

1.2 滑动楔体上的土压力

考虑墙背面和填土面都倾斜的挡土墙工况，α 为墙背面倾角，β 为墙后填土面的倾角，δ 为挡土墙和填土之间的外摩擦角，φ 为填土的内摩擦角。作用在滑动土体上的力有：滑动土楔体的自重Ws，地震主动土压力合力Pae，填土对滑动土楔体的反力R，水平和竖向地震惯性力Qhs和Qvs，如图1 所示。

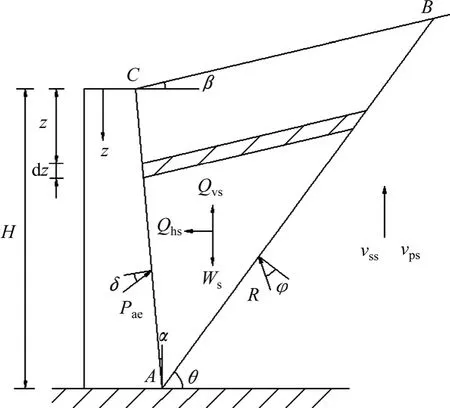
图1 挡土墙主动土压力计算模型Fig.1 Calculation model for active earth pressure of retaining wall

地震时，在填土中传播的剪切波和压缩波波速，由下式确定：

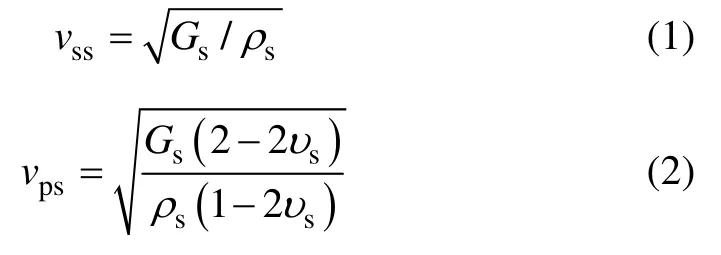
同样，在挡土墙中传播的地震波波速表示为：

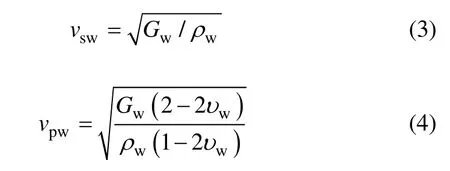
其中：ρs和υs分别为填土的密度和泊松比；ρw和υw分别为挡土墙的密度和泊松比。

假设地震时，地震加速度具有放大效应，令峰值从墙底沿高度线性增加，则有：

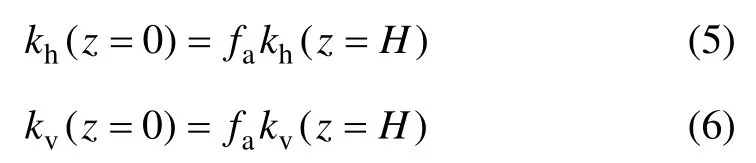
其中：fa为填土的地震加速度放大系数；kh和kv分别为墙底的水平和竖向地震加速度影响系数。

挡土墙基础的土体呈正弦稳态形式的振动，振动角频率为 ω=2π/T ，T 为地震的卓越周期，填土滑动楔体的水平和竖向地震加速度的表达式为：

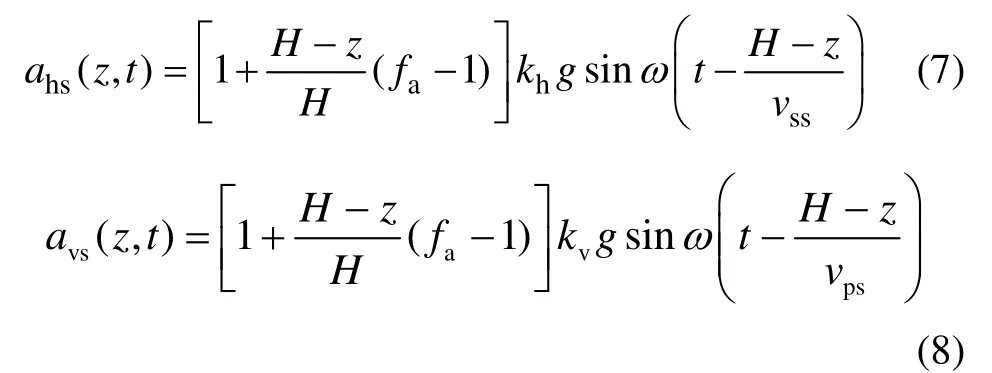
式中：g 为重力加速度；t 为时间。

由图1 的几何关系可得，与填土面平行的薄土层单元质量表示为

则填土滑动楔体受水平、竖向地震惯性力 Qhs( t )和Qvs(t )分别为：

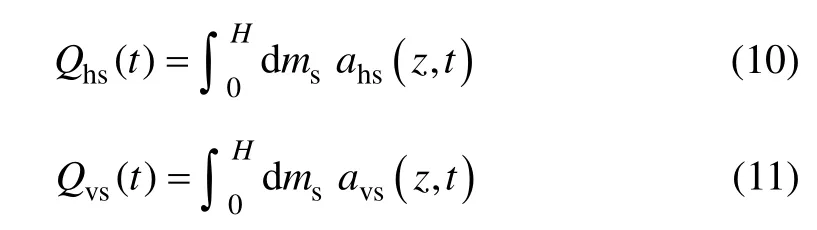
将式(7)，(9)代入(10)，整理得

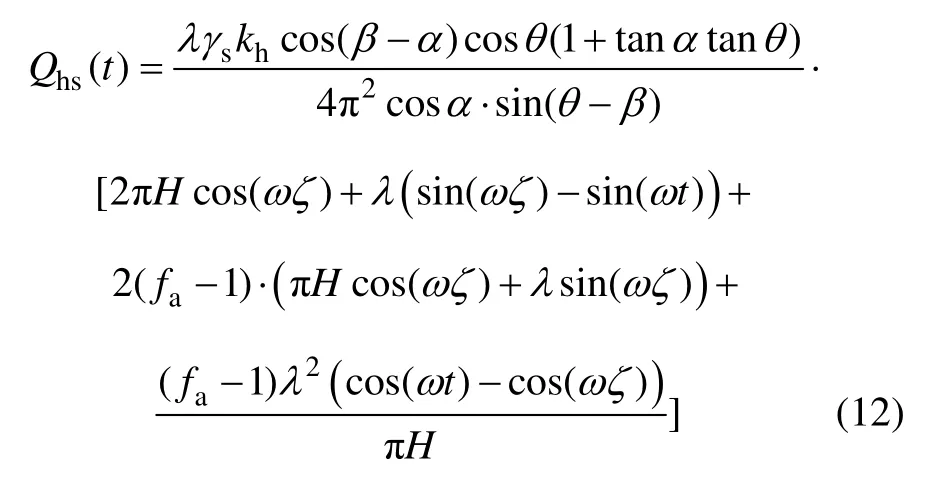
式中：λ=Tvss，为填土中的剪切波波长；ζ=t -H /vss。

同理可得：

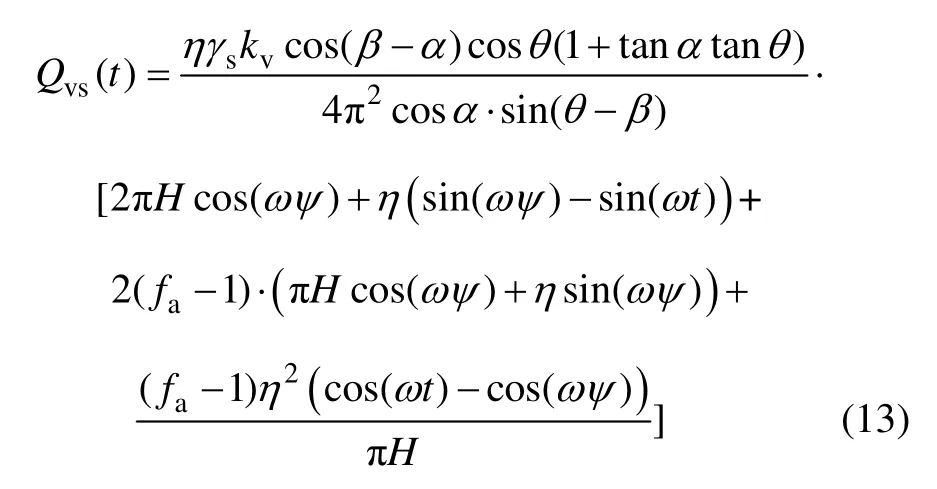
式中：η=Tvps，为填土中的压缩波波长；ψ=t -H /vps。

另外，由图1 可得，滑动土楔体的自重为

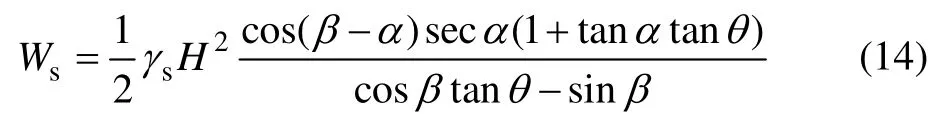
式中： γs为填土的重度。

若假定土体为刚性，且不考虑地震加速度的放大效应，即fa=1，填土的剪切波和压缩波波速趋于无穷大，则有

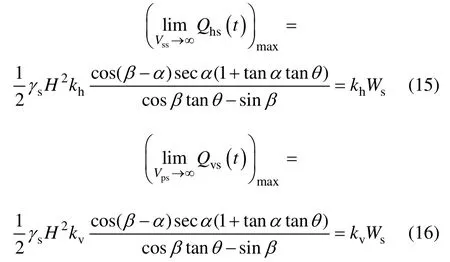
这样就退化为Mononobe-Okabe 理论中惯性力的假定情况，由此可知，拟动力法是对拟静力法的延伸扩展。

根据图1 土楔体的水平向受力平衡条件得

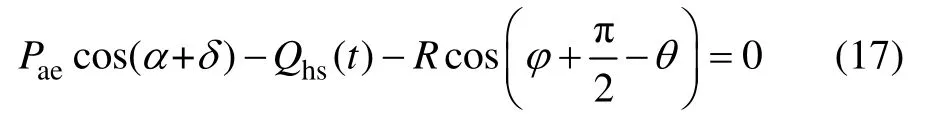
竖直向受力平衡，有

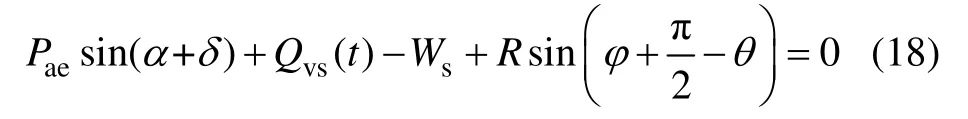
联立式(17)和(18)，则地震主动土压力合力可表示为

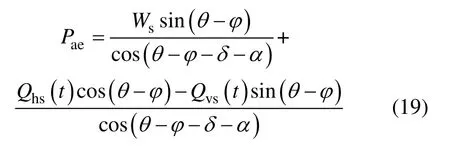
式(19)中的第1 项表示土楔体重力引起的主动土压力，第2 项表示水平、竖向地震惯性力引起的主动土压力。

1.3 挡土墙抗滑动安全系数

考虑墙面竖直和墙背面倾斜的挡土墙形式，与填土类似，当地震作用时，挡土墙也存在地震的惯性力，对挡土墙进行滑动稳定性分析，需要将惯性力计算在内，如图2 所示。类似地，假设挡土墙基础呈正弦稳态形式的振动，振动角频率为 ω=2π/T ，考虑加速度的放大效应，令峰值沿深度线性增加，则挡土墙的水平和竖向地震加速度的表达式为：

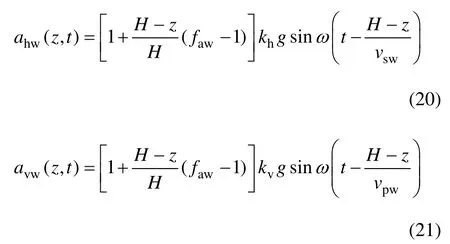
其中：faw为挡土墙的地震加速度放大系数。

图2 挡土墙滑动计算模型Fig.2 Calculation model for retaining wall sliding

挡土墙受到的水平、竖向地震惯性力为：

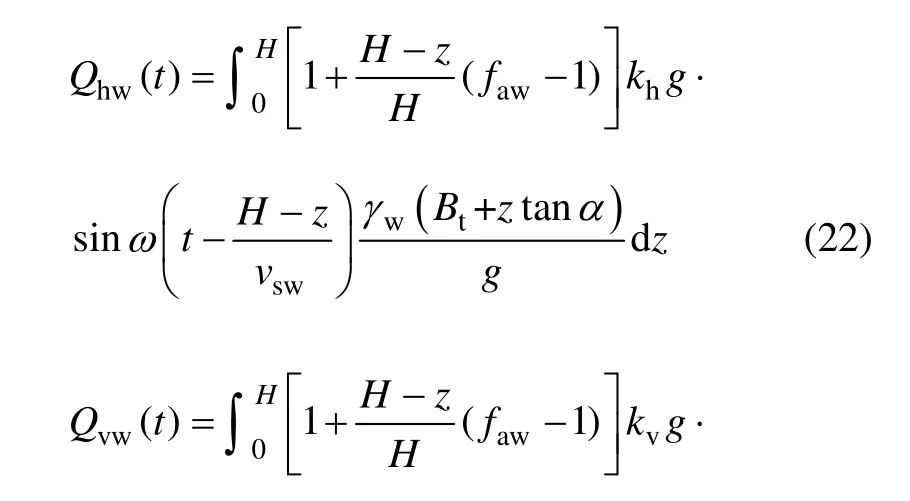
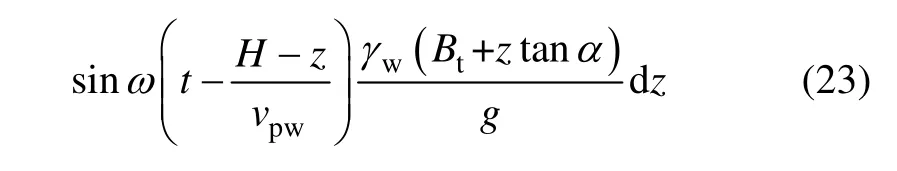
当地震作用时，墙后填土土压力的水平分力和挡土墙自身的水平惯性力共同作用，挡土墙有可能沿着基础底面发生滑动破坏，抗滑动稳定验算时，应保证土压力竖向分力和墙自重产生的基底摩阻力大于滑动力，参考《建筑地基基础设计规范》[16]的定义，将挡土墙内的地震作用惯性力考虑在内，抗滑稳定安全系数可表示为

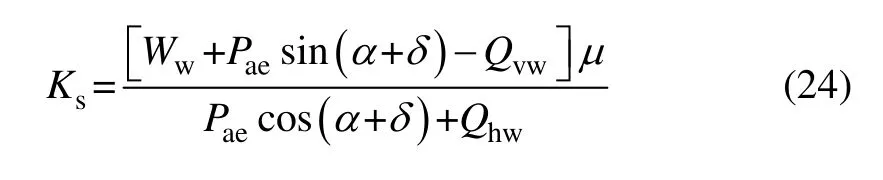
式中：μ 为挡土墙底面与土的摩擦因数，具体取值根据工程经验确定。

2 分析讨论

采用拟动力法求解地震作用下挡土墙的主动土压力时，由于剪切模量，地震波速由材料自身属性决定，都是定值，土压力归结为时间t 和滑裂面倾角θ 的函数。利用MATLAB 中的遗传算法，可以求出此多元函数的最优解，再代入抗滑动稳定安全系数的系列计算式中，可得Ks。Choudhury 等[8]提出，为防止无黏性土发生剪切流动，填土的内摩擦角应满足下列条件：

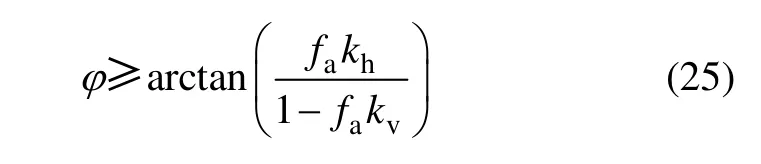
下面通过算例的对比，讨论地震放大系数、地震作用影响系数、填土内摩擦角、墙土间外摩擦角、墙背面倾角、填土面倾角等参数对挡土墙抗滑动稳定性的影响。算例中，均取以下参数[14]：H=10 m，μ =0.4，γs=18 kN/m3， γw=24 kN/m3，T=0.3 s，Bt=4 m，H/(Tvss)=0.3，H/(Tvps)=0.16，H/(Tvsw)=0.012，H/(Tvpw)=0.007 7。

2.1 地震放大系数

取参数φ=30°，δ =15°，α =10°，β =0，kv=0.5kh，fa=faw=f=1.0，1.2，1.4。当地震放大系数取不同值时，所得的抗滑稳定安全系数与水平地震影响系数的关系如图3 所示。由图3 可知：挡土墙的滑动稳定性随着放大系数的增大而降低，且地震作用越大，稳定性下降幅度越大。

2.2 地震加速度影响系数

取参数φ=30°，δ =15°，α =10°，β =0，fa=faw=f=1.2。当水平、竖向地震加速度系数取不同值时，挡土墙的滑动稳定性结果如图4 所示。由图4 可知：抗滑稳定安全系数随着地震加速度影响系数的增大而减小。例如，当kh=0.2，kv从0.5kh增大为kh时，Ks减小了14.0%，当kv=0，kh从0.2 增大为0.4 时，Ks减小了34.3%。水平地震加速度对挡土墙的抗滑稳定性有显著的影响，竖向地震加速度在水平加速度较小时，对稳定性有较大的影响。

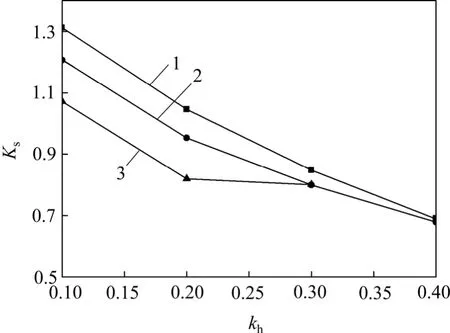
图4 地震加速度影响系数kv 对滑动稳定性的影响Fig.4 Effects of seismic acceleration coefficients on sliding stability

2.3 填土内摩擦角

取参数φ=20°，30°，40°；δ =φ/2，α =10°，β =0°；fa=faw=f=1.2。挡土墙后填土内摩擦角对滑动稳定性的影响如图5 所示。从图5 可见：当kh=0.25 时，内摩擦角φ 从20°增为30°，Ks增大27.2%，φ 从30°增为40°，Ks增大25.4%。由此可见：填土的内摩擦角越大，挡土墙的抗滑稳定性越好，且内摩擦角对稳定性有决定性的影响。

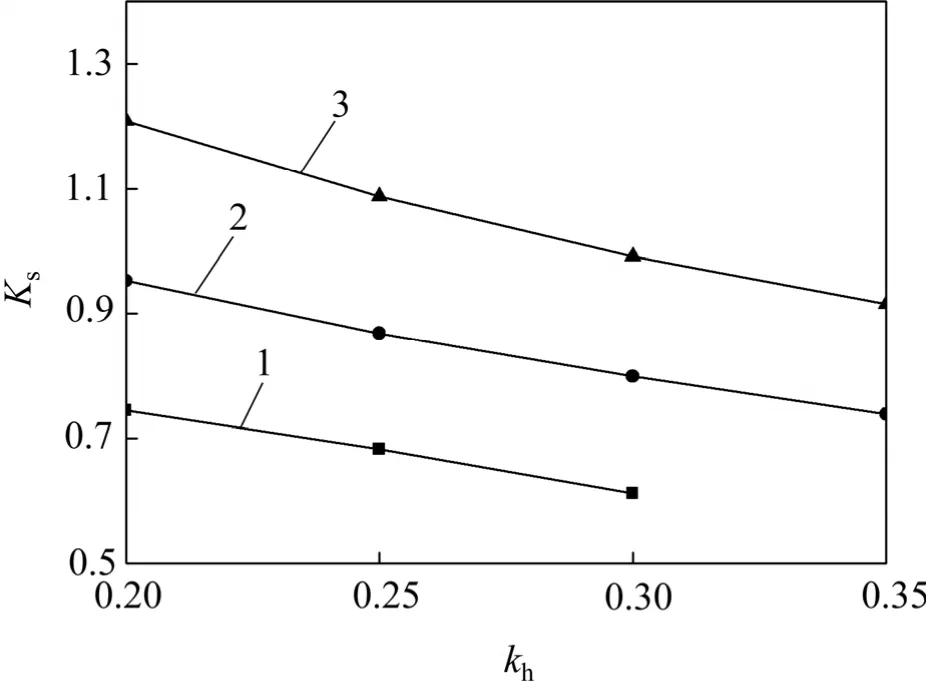
图5 填土内摩擦角φ 对滑动稳定性的影响Fig.5 Effects of soil friction angle on sliding stability

2.4 墙土间外摩擦角

取参数φ=30°；δ =0，0.25φ，0.5φ；α =10°，β =0；fa=faw=f=1.2，kv=0.5kh。墙土间外摩擦角对挡土墙滑动稳定性的影响如图6 所示。从图6 可见：由于墙土间外摩擦角主要影响了地震作用时主动土压力的竖直向和水平向的分配关系，角度越大，竖直向分量越大，水平向分量越小，挡土墙的抗滑动稳定性就越好，力学原理与计算所得结果一致。

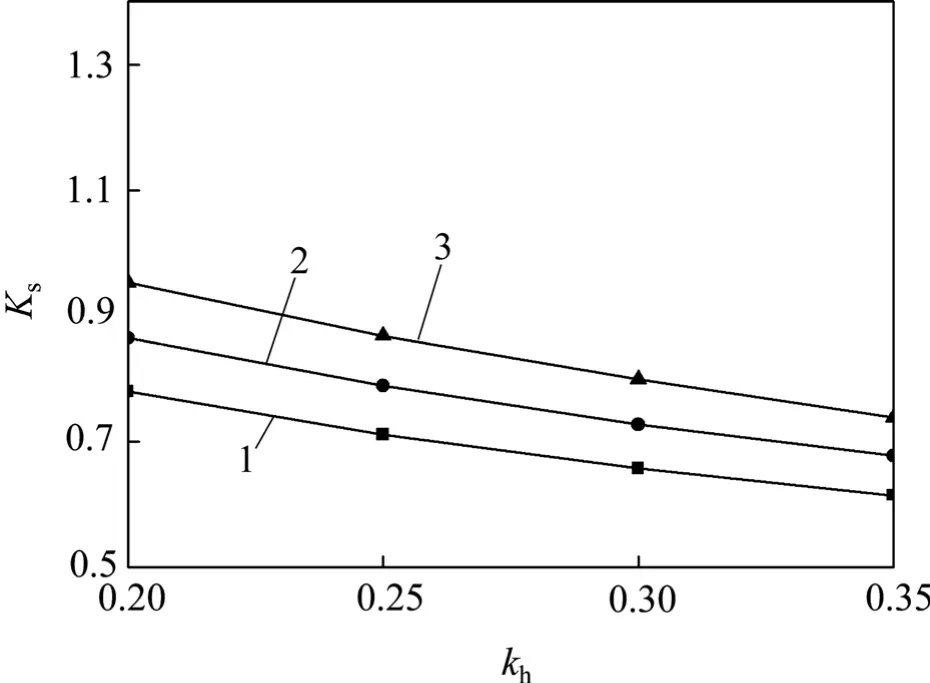
图6 墙土外摩擦角δ 对滑动稳定性的影响Fig.6 Effects of wall friction angle on sliding stability

2.5 墙背面倾角

取参数φ=30°；δ =0.5φ；α =0，5°，10°；β =0；fa=faw=f=1.2；kv=0.5kh。挡土墙墙背面倾角对滑动稳定性的影响如图7 所示。与外摩擦角作用类似，当挡土墙倾斜时，土压力含有竖向分量，不会全部作用于挡土墙的水平方向，所以，墙背面的倾角越大，抗滑动力越大，滑动力越小，抗滑动安全性就越好。

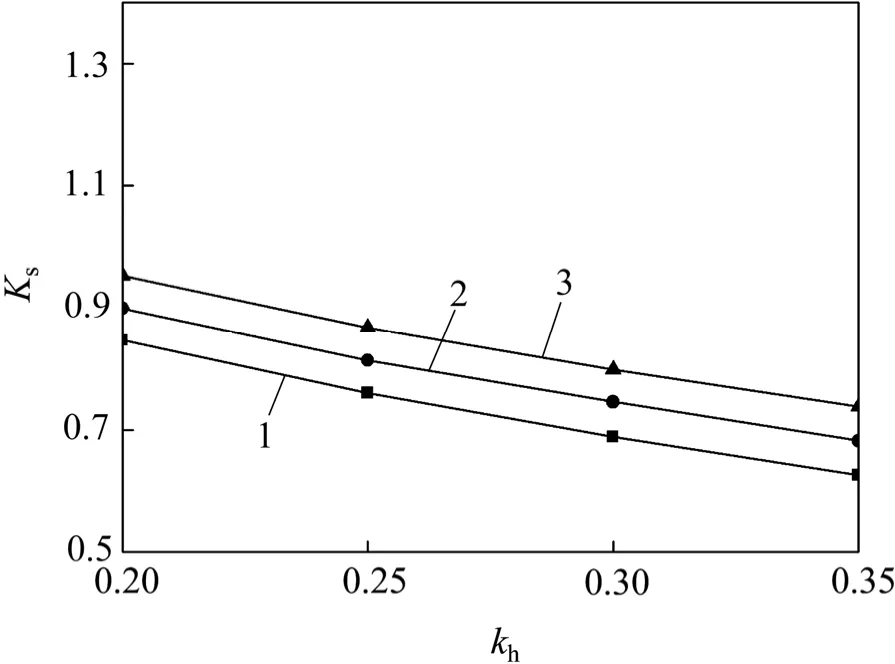
图7 墙背面倾角对滑动稳定性的影响Fig.7 Effects of wall inclination angle on sliding stability

2.6 填土面倾角

取参数φ =30°；δ =0.5φ；α =10°；β =0，5°，10°；fa=faw=f=1.2；kv=0.5kh。挡土墙墙后填土面倾角对滑动稳定性的影响如图8 所示。当kh=0.25，填土面倾角β 从0 增加到5°时，Ks降低8.8%，填土面倾角β从5°增加到10°时，Ks降低15.1%，可见抗滑动安全性系数随着填土面的增大而显著地减小。

图8 填土面倾角对滑动稳定性的影响Fig.8 Effects of backfill inclination angle on sliding stability

3 理论对比

Mononobe-Okade 方法假设挡土墙和填土受到的地震加速度沿着墙高是常量，且不随时间变化，挡土墙的地震主动土压力合力表达式为：

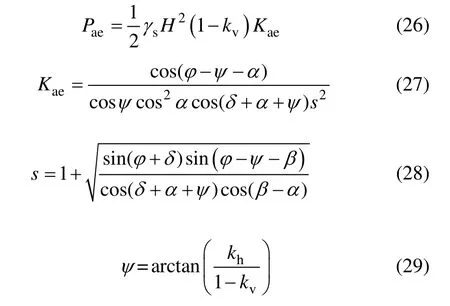
其中：Kae为地震主动土压力系数，ψ 为地震角。

取算例参数如下：H=10 m，μ =0.4，γs=18 kN/m3，γw=24 kN/m3，T=0.3 s，Bt=4 m，H/(Tvss)=0.3, H/(Tvps)=0.16， H/(Tvsw)=0.012，H/(Tvpw)=0.007 7，kv=0.5kh，fa=faw= f=1.2，φ=40°，δ =0.5φ，α =10°，β =5°，挡土墙抗滑动稳定安全系数随水平地震影响系数的变化如图9 所示。从图9 可以看出：2 种方法中滑动稳定性系数随着水平加速度的变化趋势基本一致，但是，本文方法算得的安全系数大于M-O 方法计算所得，原因主要在于拟动力法计算模型考虑了地震波传播的相位变化和时间因素，因而地震加速度沿着墙高是变化的，地震惯性力也不完全是按照地震加速度峰值计算，而M-O 方法将惯性力完全按照峰值计算，因此，拟动力法得到的挡土墙惯性力比M-O 方法的小，相应地，抗滑动稳定安全系数就比较大。

图9 不同方法的抗滑动稳定安全系数对比Fig.9 Comparison of sliding stability safe factors by different methods

4 结论

1) 采用拟动力法，考虑地震加速度的放大效应，墙背面倾角和填土面倾角，推导得出地震作用下重力挡土墙的抗滑动稳定安全系数的计算公式。该方法反映了填土和挡土墙中传播的地震波波速和相位以及材料剪切模量对滑动稳定性的影响，与真实情况更符合。

2) 挡土墙的抗滑动稳定安全系数Ks随着填土内摩擦角φ、墙土间外摩擦角δ 、墙背面倾角α 的增大而增大，当中，内摩擦角的影响作用最大；Ks随着地震放大系数、地震加速度影响系数、填土面倾角β 的增大而减小，其中，水平地震加速度影响系数kh对滑动稳定性影响显著，竖向影响系数kv在水平影响系数较小(kh＜0.25)时，对稳定性的影响较强烈，随着水平加速度的增大，kv的影响逐渐变小。

3) 与Mononobe-Okade 拟静力方法的计算结果相比，所得安全系数的变化趋势基本一致，但拟动力法计算的结果稍大，这主要是由于其考虑了土体和挡土墙材料的动力学性质影响，与真实情况更加符合，从而弥补了Mononobe-Okade 方法在理论性上的不足。

[1] Morrison Jr E E, Ebeling R M. Limit equilibrium computation of dynamic passive earth pressure[J]. Canadian Geotechnical Journal, 1995, 32(3): 481-487.

[2] Richards Jr R, Shi X. Seismic lateral pressures in soils with cohesion[J]. Journal of Geotechnical Engineering, 1994, 120(7):1230-1251.

[3] Shukla S K, Gupta S K, Sivakugan N. Active earth pressure on retaining wall for c-φ soil backfill under seismic loading condition[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2009, 135(5): 690-696.

[4] Steedman R S, Zeng X. The influence of phase on the calculation of pseudo-static earth pressure on a retaining wall[J].Geotechnique, 1990, 40(1): 103-112.

[5] Zeng X, Steedman R S. On the behaviour of quay walls in earthquakes[J]. Geotechnique, 1993, 43(3): 417-431.

[6] Choudhury D, Nimbalkar S S. Pseudo-dynamic approach of seismic active earth pressure behind retaining wall[J].Geotechnical and Geological Engineering, 2006, 24(5):1103-1113.

[7] Choudhury D, Nimbalkar S. Seismic passive resistance by pseudo-dynamic method[J]. Geotechnique, 2005, 55(9):699-702.

[8] Choudhury D, Ahmad S M. Stability of waterfront retaining wall subjected to pseudodynamic earthquake forces[J]. Journal of Waterway, Port, Coastal, and Ocean Engineering, 2008, 134(4):252-260.

[9] Ahmad S M, Choudhury D. Seismic rotational stability of waterfront retaining wall using pseudodynamic method[J].International Journal of Geomechanics, 2010, 10(1): 45-52.

[10] Ghosh P. Seismic active earth pressure behind a nonvertical retaining wall using pseudo-dynamic analysis[J]. Canadian Geotechnical Journal, 2008, 45(1): 117-123.

[11] Kolathayar S, Ghosh P. Seismic active earth pressure on walls with bilinear backface using pseudo-dynamic approach[J].Computers and Geotechnics, 2009, 36(7): 1229-1236.

[12] 王志凯, 夏唐代, 陈炜昀. 刚性挡土墙地震主动土压力的拟动力学分析[J]. 浙江大学学报(工学版), 2012, 46(1): 46-51.WANG Zhikai, XIA Tangdai CHEN Weiyun. Pseudo-dynamic analysis for seismic active earth pressure behind rigid retaining wall[J]. Journal of Zhejiang University (Engineering Science),2012, 46(1): 46-51.

[13] 夏唐代, 孔祥冰, 王志凯, 等. 挡土墙后黏性土的地震主动土压力分析[J]. 岩石力学与工程学报, 2012, 31(A01):3188-3195.XIA Tangdai, KONG Xiangbing, WANG Zhikai et al. Analysis of seismic active earth pressure of cohesive soil behind retaining wall[J]. Chinese Journal of Rock Mechanics and Engineering,2012, 31(A01): 3188-3195.

[14] 马少俊, 胡安峰, 王奎华. 地震作用下挡土墙的滑动稳定性分析[J]. 工程力学, 2012, 29(7): 209-213.MA Shaojun, HU Anfeng, WANG Kuihua. Stability against sliding analysis of a retaining wall under seismic loading condition[J]. Engineering Mechanics, 2012, 29(7): 209-213.

[15] WANG Kuihua, MA Shaojun, WU Wenbing. Pseudo-dynamic analysis of overturning stability of retaining wall[J]. Journal of Central South University of Technology, 2011, 18(6):2085-2090.

[16] GB 50007—2011, 建筑地基基础设计规范[S].GB 50007—2011, Code for design of building foundation[S].