基于电声脉冲法空间电荷测量方法的信号恢复技术研究

何 山，罗向源，朱文滔，陈 炯

（1.佛山供电局输电管理所，广东佛山 528000；2.上海电力学院，上海 200090）

1 课题研究背景

聚合物材料由于其优越的电气性能在电气设备中得到广泛的应用。现有的研究表明，这些聚合物材料在施压过程中会形成空间电荷，这些电荷所形成的库伦场与外施电场叠加，造成绝缘体中电场畸变，绝缘被击穿而引发绝缘事故。因此，近十年来，介质中空间电荷的研究，成了国际绝缘领域的一个前沿课题。

目前，基于电声脉冲法（PEA）的空间电荷测量系统，由于其系统操作方便、测量准确，广泛地用于聚合物电介质体内空间电荷分布的测量。其原理是通过脉冲电场，对空间电荷的扰动形成相应的声波，该声波的强度与电荷量成正比，利用压电传感器对声波进行测量，实现对试样中的空间电荷分布测量。由于在介质传播过程中，声波存在损耗与色散，即不同频率分量在传输过程中，其幅值衰减和传输速度都会形成不同的变化，而这些不同的变化导致含有不同频率分量的空间电荷分布信号波形产生畸变。因此，对所测量的空间电荷信号必须进行相应的恢复，得到被研究材料体内真实的空间电荷分布状态，从而为材料研究提供可靠的试验依据。

由于不同的空间电荷分布信号具有不同的频率分量，主要集中在100 MHz以内，为了解决波形稳定性差的问题，故对恢复信号频率分量限制在100 MHz以内；将介质的衰减因子看作一个传导矩阵，采用高斯函数模拟电极附近的空间电荷分布信号，通过获得不同频率下相关材料厚度的传递函数，建立相应的传导矩阵，实现真实的反应试样内全部空间电荷分布曲线波形。

利用该数据处理技术，对不同老化时间的聚合物材料的空间电荷分布信号进行了恢复，由恢复信号可知：通过信号的恢复，绝缘体中的空间电荷分布更加明显，并随着老化时间的增加，绝缘体中的缺陷增加，其空间电荷也越来越多。因此，在此基础上，探讨用空间电荷这个参数评估聚合物电老化程度的可行性问题。

2 空间电荷测量原理

PEA的空间电荷测量系统的原理图，如图1所示。

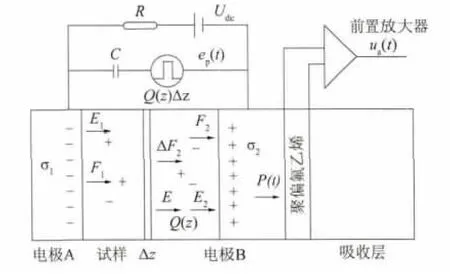
图1 PEA空间电荷测量原理

整个系统由测量电极、直流高压电源Udc和高压脉冲源ep（t）组成；整个系统的工作流程为：①利用直流高压电源在试品上形成相应的直流电场，在试样中的缺陷形成空间电荷；②在试样的电极上施加高压脉冲形成电场，试样中的空间电荷在这个脉冲电场的作用下形成相应的声波，声波的强度和电荷密度成正比；③利用压电传感器接收和测量声波脉冲，得到相应的试样中空间电荷的分布状况。

由图1可看出，设厚度为d的平板试样中，有空间电荷分布Q（t），其输出电压Ua（t）与Q（t）的数学关系式为：

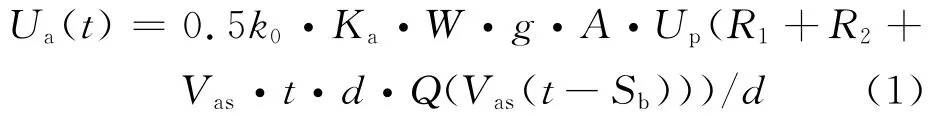
式中：g为压电应力常数；k0为声波的传播系数；W为由传感器和前置放大器的输入阻抗组成的RC回路的传递函数，取1；A为压电传感器的厚度；Ka为前置放大器的放大倍数；Up为高压脉冲ep（t）的幅值；R1为电极A上的电荷；R2为电极B上的电荷；Vas为声波的传播速度；Sb为声波在试样上的传播时间。

由式（1）可见，Ua（t）与Q（t）成线性关系，故利用PEA可以实现对介质材料中的空间电荷分布测量。

3 测量信号的恢复原理分析

由于声波在传播过程中的衰减和色散系数与结构有关，考虑到电缆以同轴结构为主，并假设空间电荷在同一半径上均匀分布，其结构示意图如图2所示，现分析图2中所示r轴方向的空间电荷测试信号。

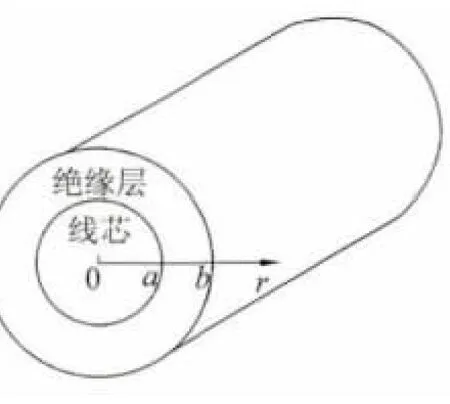
图2 电缆的结构示意图

通过对空间电荷分布信号的分解，不同频率分量信号经前置放大器输出电压信号关系式为：

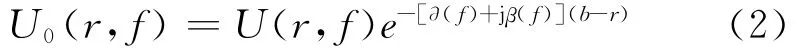
式中：U（r，f）为空间电荷振动发出的声波产生的频率为f的电压信号在半径为r处的信号；Uo（r，f）为声波经介质衰减和色散后产生的电压信号。

由同轴结构可知，直流电压下，不同半径处的电场强度为：

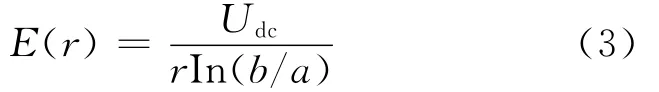
式中：a为绝缘层内径；b为绝缘层外径。

E（r）与Udc成正比。由此可见，电场强度与半径成反比：

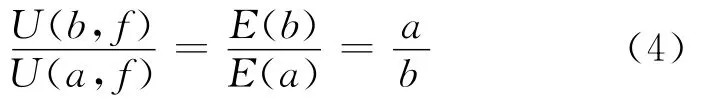
根据空间电荷分布信号可知，对于内电极信号需经绝缘层到达传感器，存在信号的衰减和色散，而外电极信号直接进入传感器，不存在信号的衰减和色散，由此可得电缆绝缘内外界面处电压信号表达式为：

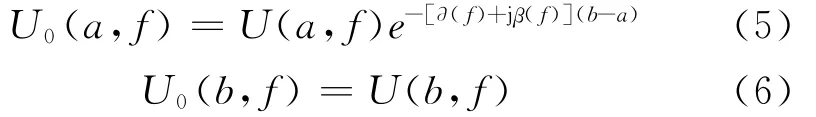
将两式相比，则：

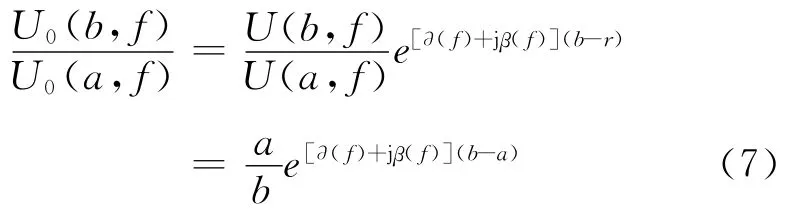
所以，不同频率分量的信号，其衰减色散系数的表达式为：

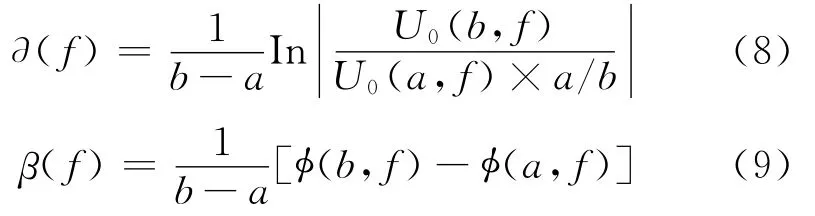
式中：φ（a，f）为U0（a，f）的相位；φ（b，f）为U0（b，f）的相位。

因此，通过对塑料绝缘层内外表面处的空间电荷分布信号的测量，由式（8）和式（9）就能求得被测绝缘材料对声波的衰减色散系数。在实际衰减色散系数计算时，定义衰变系数为：

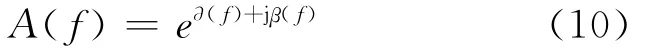
则经衰减和色散的信号表达式为：

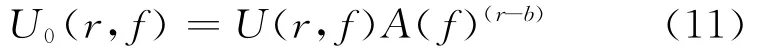
由此可见，信号恢复后的频域的表达式为：

因此，在信号恢复过程中，首先通过对低场强下空间电荷分布信息处理求得衰变系数A（f），再将衰变系数和任意电场强度下的空间电荷分布信号相结合，就可以完成对任意电场强下介质试样中空间电荷分布信号的恢复。

整个数据处理过程：首先在低场强下空间电荷测试输出信号得到Uref（t）；接着从空间电荷输出信号中提取内外电极信号Ua（t）和Ub（t），并将其进行FFT变换，分别为Uref（a，f）和Uref（b，f）；然后根据Uref（a，f）和Uref（b，f）求取A（f）；然后将场强下空间电荷测试输出信号U0（t），得到其反频域表达式U0（f）；最后进行反FFT变换得到原始时域信号U（t）。

4 Matlab仿真分析

为了实现对测量波形的恢复，在低场强下对绝缘厚度为20 mm的电缆进行测量，其空间电荷分布图如图3所示。

由图3电场下的空间电荷分布数据，得到衰减因子的计算过程：①从给定的实测波形各采样点数据的前半部分，找出绝对值最大的数据max及其位置Z1，从这个位置往前和往后寻找第1个等于max／2值的位置Z2和Z3。把Z3—Z2作为电极波形脉宽，max作为幅值。同理，在实侧波形数据的后半部分中重复上述步骤。②对测量数据进行离散傅立叶变换，得到此序列在频域中的幅值，计算出不同频率下的关于厚度的衰减因子表达式，从而建立相应的衰减因子矩阵。

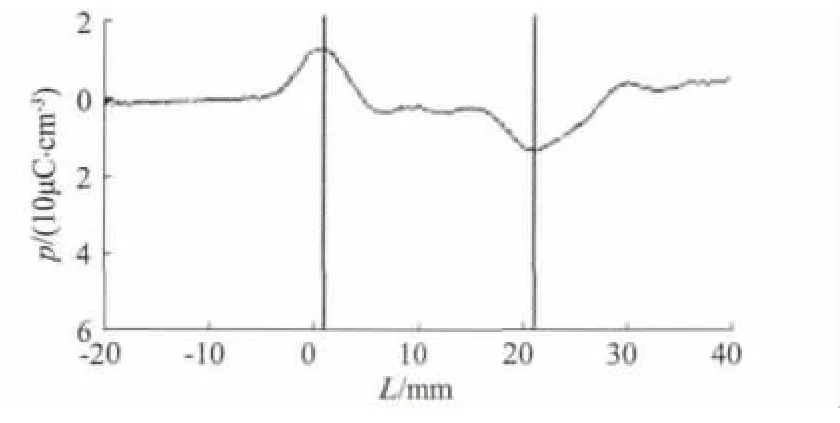
图3 电场下的空间电荷分布图

利用所得的衰减，对强场下的波形进行恢复，其恢复的波形如图4所示。

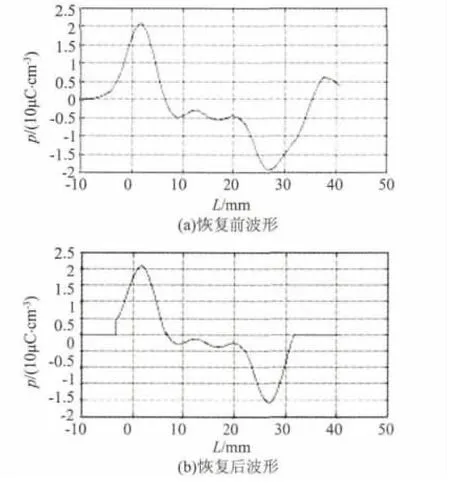
图4 测试波形的恢复图

由图4的恢复波形可以看出，通过信号恢复，使上下电极的波形对称，准确的反映出电缆绝缘中的空间电荷分布状态。

5 电缆的老化分析

对于不同老化时间的电缆进行了测量，并对测量数据进行了恢复，其波形如图5所示。

由图5可以看出，随着老化时间的增加，绝缘中的空间电荷越来越多，原因为随着运行时间的增加和老化程度的提高，电缆绝缘体中的陷阱越来越多，在电场作用下杂质发生电离，这些带电粒子在电场的作用下向两极移动，并被陷阱捕获，形成了异极性空间电荷，随着时间的增长，空间电荷越来越多。因此，对于绝缘老化程度的评估，可用空间电荷的分布状态加以评估。

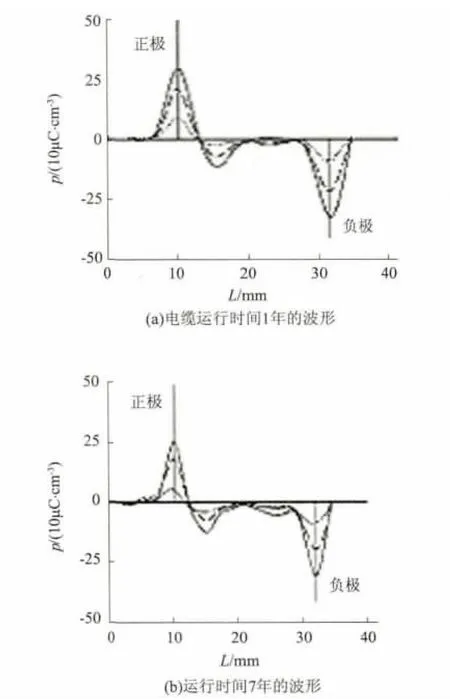
图5 不同老化时间的空间电荷曲线

6 结论

1）通过对色散和衰减模型的分析，本论文所提出的频域反卷积技术能够较好的恢复出原始的空间电荷分布信号。

2）XLPE电力电缆绝缘层中的空间电荷，随着老化时间的增加而增大，这与老化陷阱理论相一致。

3）随着老化时间的增加，绝缘层中所含的电荷量越来越大，其在绝缘层中形成的电荷库伦场越大，造成绝缘层的电场分布越来越不均匀，形成电场集中，从而导致电缆绝缘的破坏。

［1］ 尹毅，屠德民，李明，等.用等温电流法研究自由基清除剂的作用机理——聚合物电老化陷阱理论的实验验证［J］.中国电机工程学报，2000，20（3）：13-15.

［2］ 王新生，屠德民，杨会中.聚合物电老化击穿临界状态的实验验证［J］.中国电机工程学报，1993，21（增刊）：1-6.

［3］ Damamme G，Gressus C Le.S pace C harge Characterizat ion f or the21st Century［J］.IEEE Trans on DEI，1997，4（5）：558-584.

［4］ 尹毅，屠德民，王新生，等.自由基清除剂作聚合物电压稳定剂的实验研究［J］.高电压技术，1999，25（4）：18-20.

［5］ S uh K S，Koo J H，Lee S H，et al.Ef fect of sample preparat ionconditions and short chains on space charge f ormation in LDPE［J］.IEEE Trans on DEI，1996，3（2）：153-160.

［6］ Lee S H，Park J K，Lee C R，et al.The ef fect of low-molecularweight species on space charge and conduct ion in LDPE［J］.IEEE Trans on DE I，1997，4（4）：425-432.

［7］ 尹毅，屠德民，李明，等.以自由基清除剂作为电压稳定剂的作用机理的研究［J］.绝缘材料通讯，1999，（6）：12-16.

［8］ Ieda M，Nagao M，H ikit a M.High-field conduct ion and breakdownin insulat ing polymers，present situat ion and future prospect s［J］.IEEE T rans on DEI，1994，1（5）：934-944.