考虑碳排放的多目标闭环物流网络选址规划＊

沈连梅 杨勇生 杨 斌 许波桅

（上海海事大学物流研究中心1） 物流工程学院2） 上海 201306）

0 引 言

闭环物流是指企业从采购到最终销售的完整循环物流，包括产品回收与生命周期支持的逆向物流，其它目的是对物料的流动进行封闭处理，以较低的成本为顾客提供服务［1］.

目前绿色物流网络设计主要呈现3种发展趋势：正向物流、逆向物流，以及闭环物流的网络设计.正向物流网络设计中，崔娥英等［2］建立了与环境因素进行结合的单目标的绿色物流网络模型来设计物流网络，何波［3］充分考虑了物流成本和环境质量之间的平衡，Samir等［4］建立了考虑CO2排放的供应链网络设计问题.M.S.Pishvaee等［5］考虑了总成本和环境影响2个目标的平衡.

逆向物流网络设计中，赵宜等［6］通过混合整数规划模型来设计逆向物流网络，何波等［7］建立了一个纯整数非线性规划模型来解决物流网络优化问题，魏珊珊等［8］分析并确定了网络成本最优化混合整数线性规划（mixed－integer linear programming，MILP）模型，Reynaldo等［9］研究了某报废汽车逆向物流网络设计.Lee等［10］建立了3层级的总成本最优的逆向物流网络优化模型，Sibel［11］研究了多阶段逆向物流网络优化设计问题，Devika等［12］建立了基于碳足迹的逆向物流网络设计优化模型.

Saman等［13］将运营成本最小和碳排放最小作为其目标来设计网络，Saman等［14］将成本最小化目标扩展到考虑环境因素的多目标问题.

本文汲取了前人研究的优点，从正向物流和逆向物流相结合的闭合物流网络整体最优方面来选址；同时从闭环网络总成本最小、正向网络中总时间最小、闭环网络中总碳排放最小3方面来设计网络.

1 模型建立

1.1 问题描述及假设

闭环物流网络是一个从工厂、配送、客户、回收、再利用以及废弃处理的多层级网络.第一层和第二层（工厂和配送中心）节点构成的网络是整个网络的核心部分，本文的研究目的就是确定工厂和配送中心的选址位置及节点之间的运输量.

在建立模型之前作以下隐含假设：（1）客户区和再利用中心节点上不计产品的处理成本；（2）各节点之间运输时间与节点间的距离呈正相关；（3）客户区产品的回收率是恒定的，回收中心到再利用中心和废弃中心的回收比率是已知的；（4）在整个网络的设计过程中，客户区的需求必须满足.

1.2 集合参数与决策变量定义

1）｛P，D，C，K，L，M｝⊆N为所有节点集合.式中：P⊆N为所有候选工厂集合；D⊆N为所有候选配送中心集合；C⊆N为所有客户点集合；K⊆N为所有回收中心点的集合；L，M⊆N为所有再利用中心和废弃物处理中心集合.

2）W＝｛wc，wl，wm｝为节点回收率集合；G＝｛gp，gd｝为 节 点 固 定 成 本 集 合；C＝ ｛cp，cd，ck，cm｝：节点单位产品的处理成本；π＝｛πp，πd，πc，πk，πl，πm｝为节点的能力集合；E＝｛ep，ed，ek，el，em｝为节点的碳排放集合；CC＝｛cpd，cdc，cck，ckl，ckm｝为节点间的单位运输成本集合；TT＝｛tpd，tdc｝为节点间运输时间集合；EE＝｛epd，edc，eck，ekl，ekm｝为节点间单位运输碳排放集合.

3）U＝｛upd，udc，uck，ukl，ukm｝为节点间运输量集合；xp，yd，zdc∈｛0，1｝：xp，yd，zdc为 0－1变量，xp为1表示选择工厂p，否则为0；yd为1表示选择候选配送中心d，否则为0；zdc为1表示配送中心d到客户c有运输量，否则为0.

1.3 数学模型

为尽可能满足企业、客户、政府的要求，分别建立成本、时间、碳排放最小的目标函数.

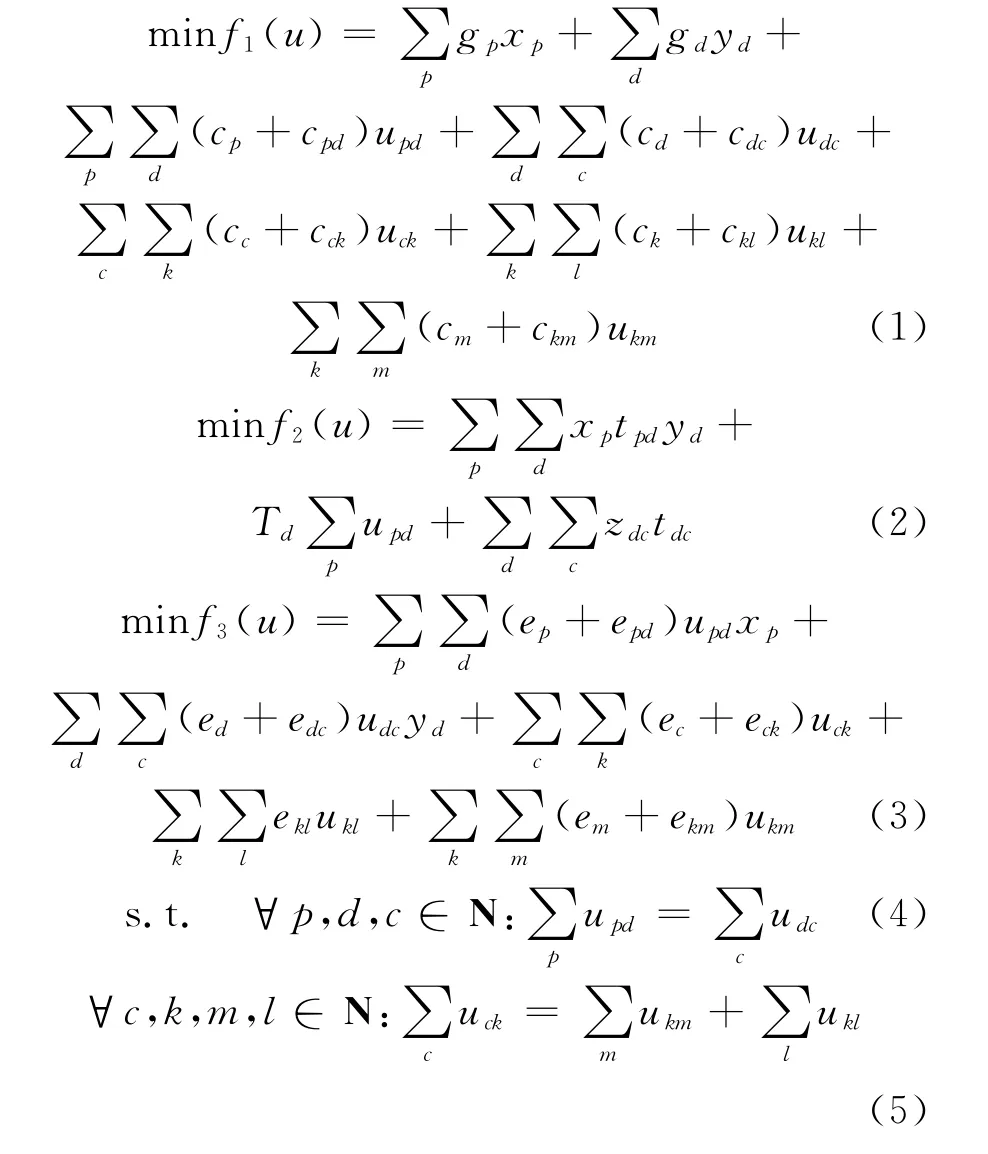
上式是一个多目标混合整数规划模型.目标函数式（1）为总成本最小，包括固定成本、节点处理成本、运输成本；式（2）为正向物流网络总时间最小，即从工厂到配送中心 再到客户的运输时间及配送中心处理时间最小；式（3）为总碳排放最小，包括个节点碳排放和节点间路径上的碳排放；约束式（4）～（8）为各节点流量平衡约束；式（9）表示客户需求必须满足约束；式（10）～（14）各节点能力约束；式（15）～（17）为参数xp，yd，zdc为0－1变量约束；式（18）为流量即决策变量的非负性约束.

模型（1）～（18）与传统的物流网络选址模型有本质上的区别：（1）考虑了正向物流和逆向物流相结合的闭环物流网络选址；（2）全面考虑了建设成本、运输成本和节点处理成本；（3）结合实际生活，考虑了闭环物流网络中正向部分即工厂—配送中心—客户的物流作业时间；最后，充分考虑了闭环物流网络选址的绿色性.

2 目标的模糊隶属度函数

由于各目标函数的最佳目标值不能确定，引用模糊数学中的隶属度定义，将目标函数模糊化后可将各个目标无量纲化，避免了原目标规划的不可共度性.令f1，f2，f3分别表示目标函数式（1）～（3）.下面为目标函数的模糊隶属函数：

式中：zi，li分别为各自目标的期望值和下限.于是把原模型目标转换为使各目标函数的隶属度尽可能接近1.若用f表示总目标值，原模型可以写成如下形式.

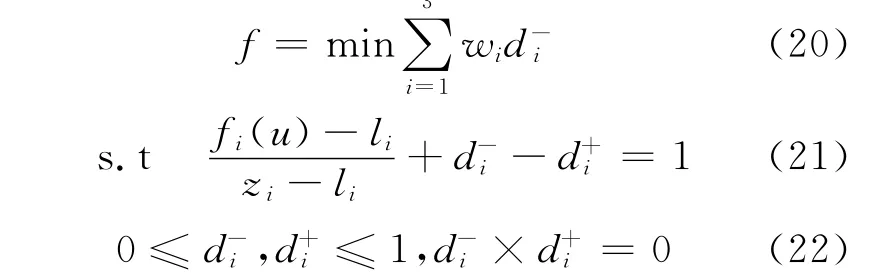
式中：wi分别表示成本目标、时间目标、碳排放目标的权重，i＝1，2，3；zi，li分别为各个目标函数的期望值和上界，zi可取作考虑单目标时的目标值，li可取作li＝2zi；d＋i，d－i分别表示目标函数的正负偏差量.然后将约束条件式（4）～（18）直接放入该目标和约束中，经过处理后的模型变成了一个普通的目标规划问题.

3 仿真算例

3.1 算例描述

算例对24个节点组成的闭环物流网络进行节点选址与分配方案的综合优化.其中对8个候选工厂（P1，P2，…，P8），4个候选配送中心（D1，D2，…，D4）选址，8个客户（C1，C2，…，C8），2个回收中心（K1，K2），再利用中心（L）和废弃处理中心（M）各1个的位置及数量均已知.任意连续2节点之间的单位运输成本、运输时间、单位运输碳排放的预算值及各节点的建设成本和单位生产或处理成本、处理时间、单位处理碳排放、节点能力均已知.

3.2 算例求解及分析

利用LINGO11.0软件包对算例进行求解.求解过程如下：分别求解成本目标、时间目标、碳排放目标值，并将其值作为各自目标的期望值，期望值的2倍作为目标上限.在确定期望值和上限前提下求解多目标规划问题，分析各目标权重在［0，1］之间变化，步长取0.1时，不同权重组合下的选址及目标值变化关系.

1）分别求解单目标的选址结果分析 见图1～3.由图可见，工厂和配送中心的选址有明显的差异.当只考虑闭环物流网络中的总成本时，选择了具有较低固定成本的 P1，P2，P6，P7，P8建工厂及D1，D4建配送中心，此时总碳排放和时间消耗较大；当顾客对配送时间要求较高时，选择了比较集中的P4，P5，P6建设工厂，此时建立了4个配送中心总成本较高；当政府和消费者对环境要求较高时，选择了碳排放较小的P2，P4，P5，P7.

图1 总成本最小网络图

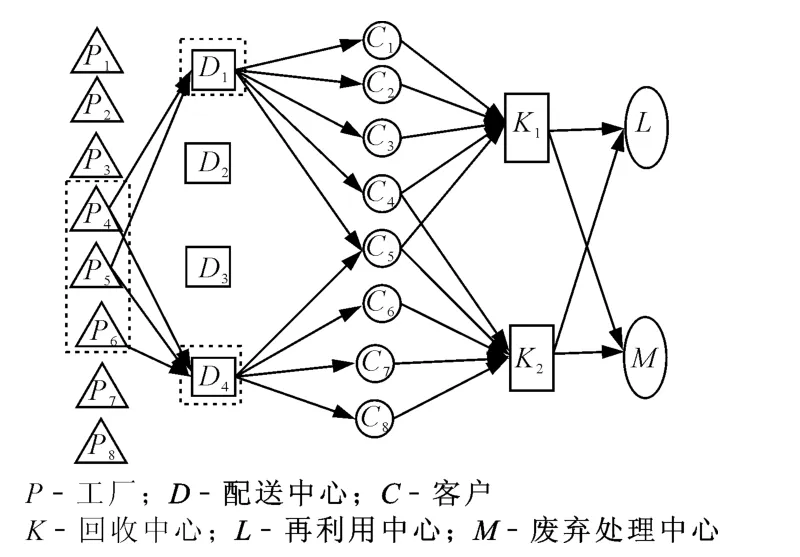
图2 总时间最小网络图

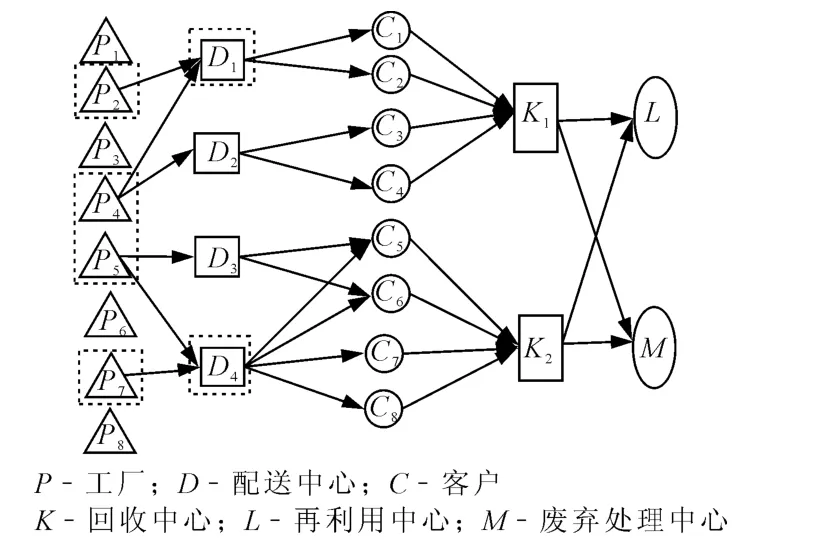
图3 总二氧化碳排放最小网络图

2）时间－碳排放－成本权重变化对总目标值的影响 时间权重由0.2，0.3，0.4动态变化时，时间－成本－碳排放权重变化对总目标的影响见图4.碳排放权重由0.4，0.5，0.6动态变化时，时间－成本－碳排放权重变化对总目标值的影响见图5.其中横轴均表示成本目标权重值，纵轴均表示总目标值.

由图4可见，时间权重恒定（如w2＝0.4）时，成本权重和碳排放权重对总目标的影响相悖反，但对于系统总目标影响较大的是成本因素.当成本权重恒定时（如w3＝0.3）时，时间权重和碳排放权重对总目标影响较小.由图5可知，碳排放权重恒定（如w3＝0.6）时，成本权重和时间权重对总目标的影响相悖反，但对于系统总目标影响较大的是成本因素.当成本权重恒定时（如w3＝0.2）时，时间权重和碳排放权重对总目标影响较小.

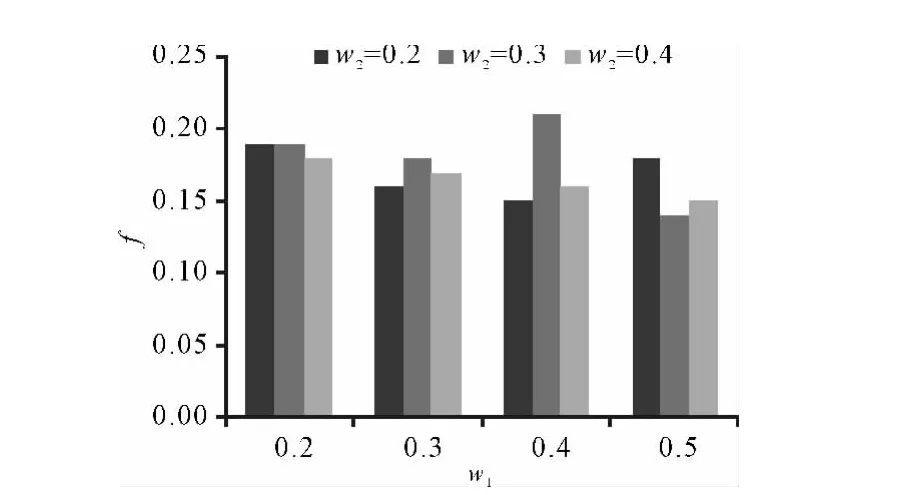
图4 时间－成本－碳排放权重变化对总目标影响

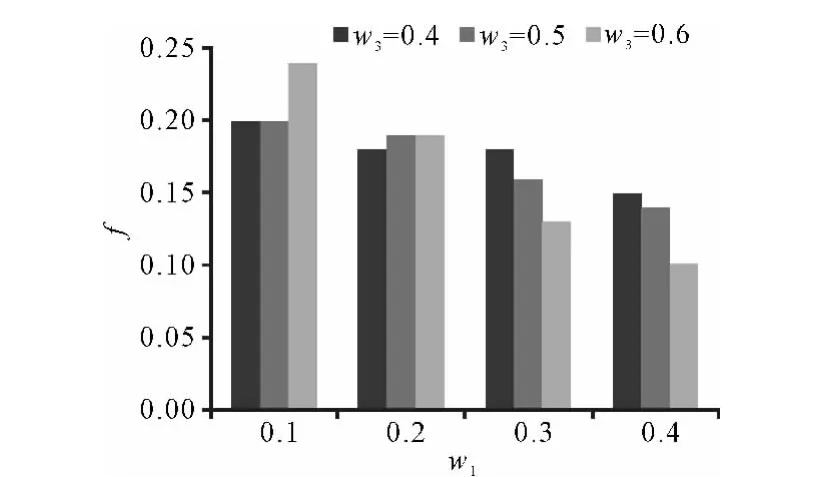
图5 时间－成本－碳排放权重变化对总目标影响

4 结束语

本文以闭环物流网络建设成本和运营成本最小、总正向物流时间最小、总二氧化碳排放最小为目标，提出了节点选址和物资分配相结合的多目标优化模型.在求解中引入模糊数学中的隶属度概念，将多目标规划问题转化为求解目标规划问题.最后通过仿真算例证实该模型和算法的有效性，并研究比较了单一目标下选址及不同权重下对总目标函数值的影响情况.

结果表明，分别考虑单一目标时选址结果有明显的差异；多目标不同权重对选址结果有明显的影响，成本权重越大，设施选择在总成本较低的地方；碳排放权重越大，设施选择在总碳排放较小的地方；不同权重对总目标函数值的影响有明显差异，时间权重恒定时，成本权重、碳排放权重对总目标值的影响相悖反，碳排放权重恒定时，成本权重、时间权重对总目标值的影响相悖反，但对于系统总目标影响较大的是成本因素.

［1］许国君.闭环供应链下的配送和库存理论及应用［M］.北京：中国物资出版社，2007.

［2］崔娥英，罗俊浩，季建华.碳税和碳交易环境下的物流网络设计问题研究［J］.科技管理研究，2012，32（22）：239－242.

［3］何 波.绿色物流网络系统建模与效率边界分析［J］.中国管理科学，2012，20（3）：138－144.

［4］SAMIR E，RYAN M.Green supply chain network design to reduce carbon emissions［J］.Transportation Research，Part D，2012，17：370－379.

［5］PISHVAEE M S，TORABI S A.Credibility－based fuzzy mathematical programming model for green logisticsdesign under uncertainty［J］.Computers ＆Industrial Engineering，2012，62：624－632.

［6］赵 宜，尹传忠，蒲 云.回收物流设施多层选址模型及其算法［J］.西南交通大学学报，2005，40（4）：530－534.

［7］何 波，杨 超，任鸣鸣.基于第三方物流的产品回收物流网络优化模型及算法［J］.计算机集成制造系统，2008，14（1）：39－44.

［8］魏珊珊，张科静.电子废弃物逆向物流网络选址优化模型设计［J］.东华大学学报：自然科学版，2010，36（5）：574－580.

［9］REYNALDO C R，JüRGEN E.Reverse logistics network design for the collection of end－of－life vehicles in Mexico［J］.European Journal of Operational Research，2009，196：930－939.

［10］LEE Jeongeun，MITSUO G.Network model and optimization of reverse logisticsby hybrid genetic algorithm［J］.Computers ＆ Industrial Engineering，2009，56：951－964.

［11］SIBEL A A，STEFAN N F.Multi－period reverse logistics network design［J］.European Journal of Operational Research，2012，220：67－78.

［12］DEVIKA K，ALI D，MAHMOUD A.A carbon footprint based reverse logistics network design model［J］.Resources Conservationand Recycling，2012，67：75－79.

［13］MIR S P，JAFAR R.Environmental supply chain network design using multi－objective fuzzy mathematical programming［J］，Apllied Mathematical Modelling，2012，36：3433－3446.

［14］SAMAN H A，ZU Guoqing.A multi－objective facility location model for closed－loop supply chainnetwork under uncertain demand and return［J］.Applied Mathematical Modelling，2013，37：4165－4176.