地下管道群中安装电缆的热状态及载流量评估

刘 斌，张 龙，孙振权，陈西平，张 伟

（1.陕西省地方电力集团，西安 710061；2.西安交通大学电气工程学院，西安 710049）

0 引言

为了确保地下电缆的安全可靠运行，近年来很多电力公司在新建电缆线路上安装了分布式光纤测温系统（DTS），直接测量电缆表面的温度，实现对整条电缆线路热状态的实时在线监测。根据测得的电缆表面温度数据，利用IEC 60287标准推荐的方法可以计算出电缆绝缘层温度，以此评估电缆的热状态［1－6］。

对没有安装DTS的220 k V电缆线路，陕西省地方电力集团公司开展了深入研究。首先，技术人员沿线路进行勘测，发现存在220 k V电缆在变电站周围被敷设于地下深埋的管道群中的问题，而不利的运行环境可能导致电缆过热，形成线路载流量的“瓶颈”，因此有必要开展对这些位置电缆的热状态监测。

针对这个问题，电力公司一般采用在电缆表面安装热电偶［7］的方法对电缆的热状态进行监测，但在具体实施过程中，由于管道的存在大大增加了在电缆表面安装热电偶的难度，而挖掘并打碎管道安装热电偶既不安全也不实际。因此，不得不将热电偶安装于管道群外面，但存在如何利用测到的管道群外部传感器温度来推算电缆绝缘层温度的问题。本文提出一种采用拟合计算温度和管道群外部传感器的测量温度的方法，来推算电缆绝缘层温度。

1 估算方法

1.1 土壤热参数估算

220 k V管道群电缆线路的典型横截面敷设图如图1所示。

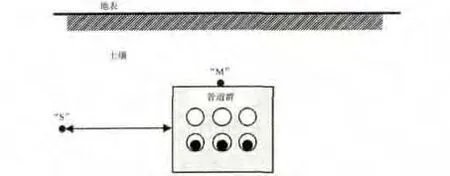
图1 一条管道群电缆线路的横截面敷设图

该管道群由上下两排管道组成，电力电缆敷设于下排管道，引导电缆穿入上排管道。热电偶安装在管道群外部（在图1的M点），用以监测温度和评估电缆的热状态。在距离电缆16 m远处安装另外一个热电偶（在图1的S点），测量所得的土壤温度为Tsoil。

当电缆和管道群敷设条件确定后，对于特定的负载电流温度分布只取决于周围土壤的热特性和土壤温度。假设T为任意一点的温度，它是土壤热阻系数ρsoil、土壤热扩散系数δsoil和土壤温度Tsoil的函数。这些未知参数可以通过拟合计算温度和安装在管道群外部M点的传感器的测量温度来估算。

此拟合过程可通过求解式（1）中目标函数F（x）的最小值而获得。

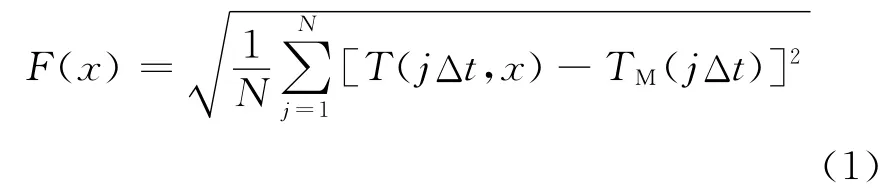
式中：N是离散测量次数；x是土壤热参数；T（t，x）和TM（t）分别是M点的计算温度和测量温度。

F（x）最小值的计算和载流量的计算涉及温度场的数值分析和优化算法两种。利用这两种方法，使得求解F（x）最小值的过程大大简化，这样式（1）中x的3个未知的参数可简化为x＝ρsoil。

ρsoil和δsoil用经验公式联系起来［8］，表达式为：

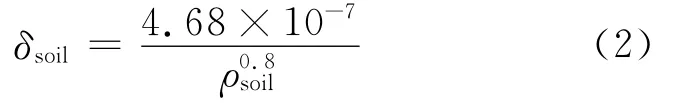
1.2 电缆热状态和载流量的评估

利用估算的土壤热阻率、负荷和土壤温度，可用IEC 60287推荐的方法或现代数值方法计算电缆的绝缘温度，评估电缆热状态和载流量。另外，在特定的持续时间或过负荷条件下的电缆允许载流量也能得到预测。

2 电缆的温度场及求解方法

管道群敷设电缆的温度分布可以简化为一个二维温度场。采用有限元法分析温度场，得到简化的温度场域如图2所示，选取宽30 m和深15 m的长方形区域作为计算区域。

图2 简化的温度场域

温度场的基本导热微分方程表达式为：

式中：x，y为空间坐标，m；T为温度，K；ρ为相应材料的热导率，K·m／W；cp为单位体积热容，J／（K·m3）；t为时间，s；q为产热率，W／m3。

选用有限元法来求解方程（3），关于该方法的详细内容见文献［9］。

3 优化方法

有许多优化方法可用来求解式（1）中目标函数F（x）的最小值。本文采用四等分法［10］，利用量值等分产生一新的点和一个新的区间，完成这种算法的主要步骤如下：

1）选择区间下限a和上限b，使xm＝（a＋b）／2，L0＝L＝b－a，计算F（xm）。

2）设x1＝a＋L／4，x2＝b－L／4，计算F（x1）和F（x2）。

3）如果F（x1）＜F（xm），设b＝xm；xm＝x1；转向第五步，否则继续第四步。

4）如果F（x2）＜F（xm），a＝xm；xm＝x2；转向第五步；否则，设a＝x1；b＝x2；转向第五步。

5）重复第二步直到满足参数x的相对变化值不大于1%，表达式为：

4 实例分析

本节进行一个典型的实例分析，介绍了3条220 k V／250 MVA管道群线路的基本情况，然后通过估算土壤热参数对这3条线路的热状态进行评估。

4.1 基本情况

220 k V变电站的3条线路入站平面图如图3所示，其中2号和3号线路平行入站。3条管道群敷设横截面图如图4所示。

每个管道群长约10 m并且由双排管道组成，电力电缆敷设于下排管道中。为了使埋设较深的电缆具有良好的散热性，用膨润土混合物填充电缆管道空气层［1］。

图3 220 k V变电站的三线路入站平面图

为了监测电缆的热状态，一个热电偶被安装在1号线路管道群的上表面M点，另一个被安装在距离电缆管道群15 m远，深2.5 m处的S点监测土壤温度。考虑到1号线路土壤热阻率估算完成后，便可以计算出2号和3号线路的电缆绝缘层温度，因此2号和3号线路的热状态没有被监测。

利用有限元法进行求解时，需要将场域进行离散化，可用Matlab软件来完成。一个由三角形网格和节点组成的1号线路的离散场域如图5所示，其中包含2 737个节点和5 364个剖分单元。由于该区域关于Y轴对称，所以仅对区域的一半进行离散化。

4.2 估算土壤热阻率

图6和图7中曲线记录了连续6天的电流和温度数据。从图中可看出，深度为2.5 m时的土壤温度波动很小。前72 h，利用所测到的管道群表面温度和求得的式（1）的F（x）极小值，估算参数x＝ρsoil。设初始区间［a，b］＝［0.001，3.0］，得到土壤热阻系数的估算值ρsoil＝0.83℃·m／W。

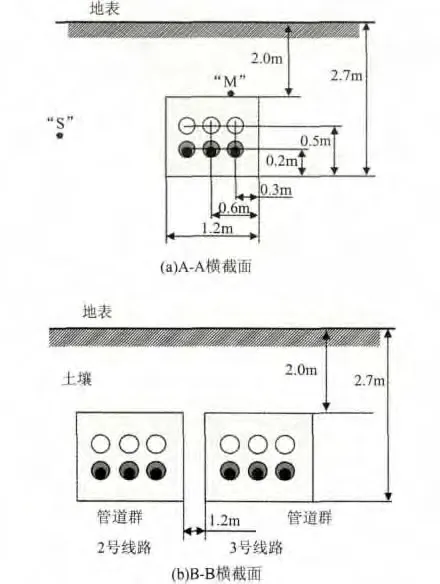
图4 3条管道群敷设横截面图

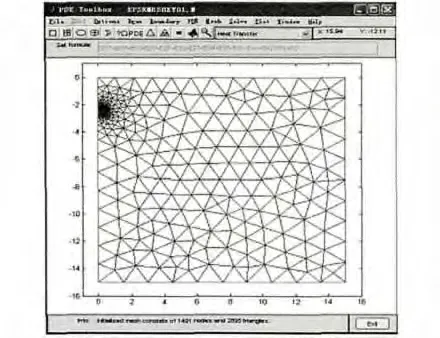
图5 三角形网格和节点组成的离散场域

此估算值与便携式热阻率测量仪器KD2所得的三次测量值0.78、0.80、0.80℃·m／W基本一致。

利用估算的热阻系数和图6所示后72 h期间的负荷电流，可预测管道群表面温度，而该预测温度同样可以在图6中看到。由此可以看出预测温度与测量温度具有很好的一致性。

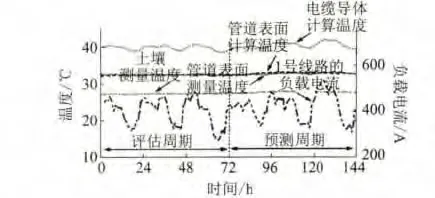
图6 1号线路连续6天的测量温度、负载电流和计算温度

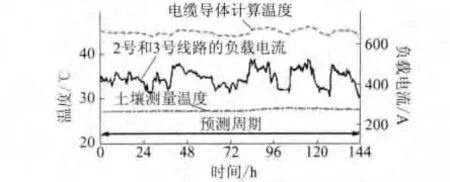
图7 2号和3号线路连续6天的测量温度和计算温度

4.3 对3条线路绝缘层热状态和载流量的评估

4.3.1 绝缘层温度计算

电缆的热状态通常以导体温度表征，可通过有限元程序计算出来。

由图6和图7可以看出，1号线路的绝缘层温度最高达42.2℃，2号和3号线路最高温度达46.3℃。显然，在当前运行条件下，绝缘层温度远低于允许温度90℃。

4.3.2 载流量评估

1）长期运行的额定载流量 表示在电缆导体温度不超过允许温度90℃时，电缆运行时的最大恒定负载电流。在ρsoil＝0.83℃·m／W，Tsoil＝27.2℃和电缆导体最高允许温度为85℃的条件下，计算出1号线路运行时最大电流约为702 A，是其额定电流值627 A（在ρsoil＝1℃·m／W，Tsoil＝25℃条件下计算出的额定值）的1.12倍。计算出2号和3号线路的最大电流是其额定电流值的1.02倍。因此，操作人员可允许分配比额定电流值高的负荷电流。

2）紧急载流量 指电缆在特定持续时间内能运行的最大过载电流，此时电缆导体温度不超过容许值90℃，应急载流量值取决于已加载电流的时间和线路可能承受过载的持续时间。而在ρsoil＝0.83℃·m／W，Tsoil＝27.2℃和电缆导体最高允许温度为90℃的条件下，计算不同应急载流量下的允许持续时间。

图8为在72 h末，1号线路突然承受1 567 A电流，相当于额定电流值627 A的2.5倍。从图8中可知，在过载运行23.5 h后，电缆导体温度达到90℃。

进一步计算得到：1号线路过载电流为额定电流的300%和270%时，持续时间分别为4.6 h和11.1 h；2号和3号线路的过载电流为额定电流的300%、270%和250%时，持续时间分别为2.2、6.5和13.8 h。关于应急载流量的预测，在系统发生意外状况时非常有助于调度员进行合理调配负荷。

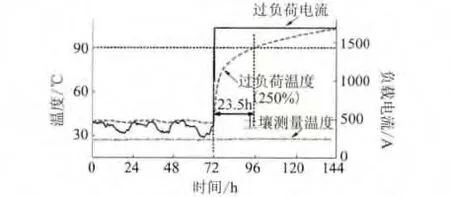
图8 1号线路施加250%过载电流时的导体温度

上述计算指出3条线路都是处于轻负载运行中。但需要强调的是，以上计算是基于当前的土壤热状态，而土壤的热特性可能随着天气的变化而改变。因此，当土壤的热阻和温度发生显著变化时，只要管道群表面的计算温度和测量温度之差超过一定的值，土壤热阻系数的估算和载流量的预测将是一个连续进行的过程。

5 结语

本文研究了一种通过从测量到的土壤温度推测土壤热参数，进而间接评估电缆热状况和载流量的方法，实际应用于220 k V变电站入线的3条220 k V／250 MVA地下管道群敷设电缆线路。研究结果显示：土壤热阻率的估算值与实测值相一致；预测温度值与测量值有很好的一致性；在当前土壤的热阻率ρsoil＝0.83℃·m／W和土壤温度Tsoil＝27.2℃条件下，3条线路都处于轻负荷运行。因此，对于评估地下管道群电缆的热状态和载流量，本文提出的方法是有效的。

［1］ 马国栋.电线电缆载流量［M］.北京：中国电力出版社，2003.

［2］ NAH MAN J，TANASKOVIC M.Determination of the Current Carrying Capacity of Cables Using the Finite Element Method［J］.Electric Power Systems Research，2002，61（2）：109-117.

［3］ 梁永春，孟凡凤，王正刚，等.土壤直埋电缆群额定载流量的计算［J］.高压电器，2006（04）：244-246.

［4］ 罗俊华，周作春，李华春，等.电力电缆线路运行温度在线检测技术应用研究［J］.高电压技术，2007，33（1）：169-172.

［5］ 彭超，赵健康，苗付贵.分布式光纤测温技术在线监测电缆温度［J］.高电压技术，2006，32（8）：23-24.

［6］ Garrido C，Otero A F and Cidras J.Theoretical model to calculate steady-state and transient ampacity and temperature in buried cables［J］.IEEE Trans.on Power Delivery，2003，18（3）：667-678.

［7］ Nelson R J，Brennan T F and Engelhardt J S.The application of real-time monitoring and rating to HPOF pipe cable systems［J］.IEEE Trans.on Power Delivery，1989，4（2）：850-856.

［8］ Neher J H.The transient temperature rise of buried power cable systems［J］.IEEE Trans.Power Apparatus and Systems，1964，83（2）：102-111.

［9］ 孔祥谦.有限单元法在传热学中的应用［M］.北京：科学出版社，1998.

［10］凌永祥，陈明逵.计算方法教程［M］.西安：西安交通大学出版社，2005.