球带法求光通量的误差分析及改进
徐海涵
(国家广播电视产品质量监督检验中心,北京 100015)
1 球带法简述[1]
如图1所示,由已知光强分布I(φ,θ)求总光通量的公式如下:
(1)
Ftot为总光能量,φ和θ的含义如图1所示,以下相同。
求部分光通量的公式为:
(2)
对于轴对称光源,式(1)、式(2)变为:

(3)
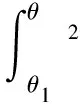
(4)
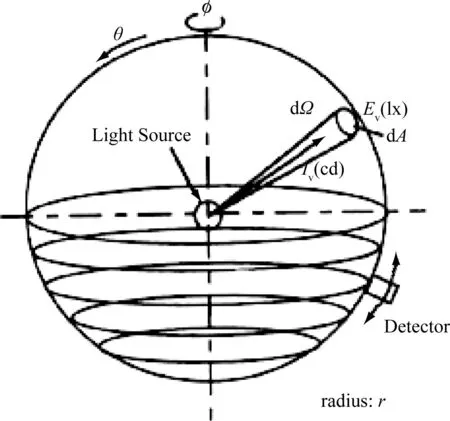
图1 光强积分示意图Fig.1 Schematic drama: luminous intensity integrating
球带法是为了简化分布式光度计的测量和计算而对式(3)和式(4)作出的一些变化。如图2所示,将球面分成许多球带,各个球带对应的光强分别为I1,I2,I3,……,In,这时由式(4)可以推导出各球带所对应的光通,如下:

图2 球带的分割Fig.2 Schematic drama: Division of sphere-band


(5)
式(5)中Fi为第i个球带的光通量,θ含义见图2,注意θ是从θ0到θn。
总光通量为:
(6)
式(5)为球带法计算光通量的基本公式。按照球带的分割方法,球带法还可分为等角度法和等立体角法,其基本原理是相同的,在此不再详述。
2 对球带法公式的改进
从球带法的基本公式(5)的推导过程可以看出,式(5)成立的条件是在整个球带上光强I是一个常数;式(6)成立的条件是I为以下这样一个非连续的函数:
但这与实际的情况是不同的。实际上,I随θ是连续变化的;在每一球带上,假定I随θ是线性变化的,这更符合实际的情况。在这个前提下,我们将对球带上的光通量公式进行重新推导。
设球带边界的θ角分别为θi-1和θi,光强I随θ线性变化,其斜率是a,中心点(θi-1+θi)/2的光强为Ii,此Ii也就是式(5)中的球带对应的光强。任意θ角的光强公式如下:



=2πa[(sinθi-θicosθi)-(sinθi-1-θi-1cosθi-1)]+2πb(cosθi-1-cosθi)
(7)


=2πIi(cosθi-1-cosθi)+2πa[(sinθi-θicosθi)-(sinθi-1-θi-1cosθi-1)]-πa(cosθi-1-cosθi)(θi-1+θi)

(8)
式(8)为改进后球带法(以下称其为新球带法)的基本公式。以示区别,把本文第1节中的方法称为旧球带法,其基本公式为式(5)。
3 旧球带法误差分析
比较式(8)和式(5),可以看出:它们的前半部分[2πIi(cosθi-1-cosθi)]是相同的,差异在式(8)的后半部分,这一部分即为旧球带法的误差,记为:
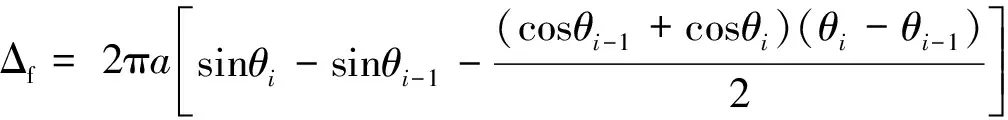
(9)
以下对这一误差进行详细分析。
首先,误差与a成正比,即在某一球带两边界的光强相差越大,则用旧球带法计算光通的误差越大。其次,除a以外的部分:
(10)
姑且称之为“误差因数”,是一个只与θ角以及Δθ(即θi-θi-1)相关的量,其与θ角及Δθ的关系如图3所示。

图3 旧球带法“误差因数”与θ角以及Δθ的关系Fig.3 Correlation curve between the error factor of old sphere-band method and θ for different Δθ
从图3中可以看出:此“误差因数”在两极部分最大,在“赤道”附近最小。实际上,如果分成上下两个半球的话,它们是对称的,这一点很好理解。另外,此“误差因数”随Δθ的减少而快速减小,即球带划分划细,则误差越小。在Δθ分别为1°、5°、10°时,对同一球带进行光通量计算(假定a相同),其光通量误差分别相差约1个数量级。同时,这一“误差因数”有正有负,因此在计算整个空间的光通量时,有可能有相互抵消的作用,从而有可能使总光通量的误差减小。
4 实例分析与验证
以下通过实例进行分析与验证。前面的几个例子I分布是特例(在现实中不一定存在),但通过式(3)能积分计算出光通量,由此可对新旧球带法进行验证;后几个是实际光源光强分布的实例。
4.1 半空间线性分布(见图4)
由表1结果可见,旧球带法在Δθ较大的情况下计算结果与实际光通量值有较大误差,Δθ为10°的情况下误差为0.445%,5°情况下约为0.1%;到Δθ为1°时误差才能减小到基本可以忽略的程度。而用新球带法计算则不存在误差。
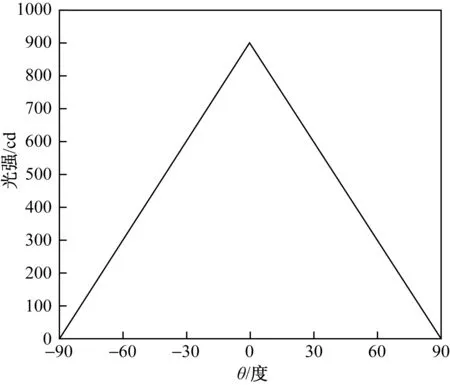
图4 验证实例4.1的光分布:半空间线性分布Fig.4 Luminous intensity distribution of example 4.1: semi-direction linear

表1 实例分析与验证:半空间线性分布计算结果Table 1 Result of example: semi-direction linear distribution
4.2 全空间线性分布(见图5、表2)
从总光通量来看,新旧两种方法计算出的结果是相同的,并且误差为0。但如果单独计算下半球或上半球光通量,就会发现与实例1中相同的情况,即Δθ较大时误差较大。只不过下半球是正误差、上半球是负误差,对总光通量来说,正负误差相加刚好给抵消掉了。这正是在第3节中分析过的计算全光通量时误差抵消的实例。

图5 验证实例4.2的光分布:全空间线性分布Fig.5 Luminous intensity distribution of example 4.2: omni-direction linear

表2 实例分析与验证:全空间线性分布计算结果Table 2 Result of example: omni-direction linear distribution
4.3 LED射灯No.1(见图6、表3)
Δθ为10°时,新旧方法计算结果误差为4.24%、2.19%,Δθ为5°时则分别为1.07%、0.55%。由结果可见:当Δθ较大时,由于未能准确体现出光源光强分布的真实情况,因此Δθ为10°和5°时两种方法求出的光通量误差都比较大,但相对而言用新球带法计算出的误差更小,更接近真实光通量值。

图6 验证实例4.3:LED射灯No.1的光分布Fig.6 Luminous intensity distribution of example 4.3: LED reflector lamp No.1

表3 实例分析与验证:LED射灯No.1Table 3 Result of example: LED reflector lamp No.1
4.4 LED射灯No.2(见图7、表4)
其结果与实例4.3类似。
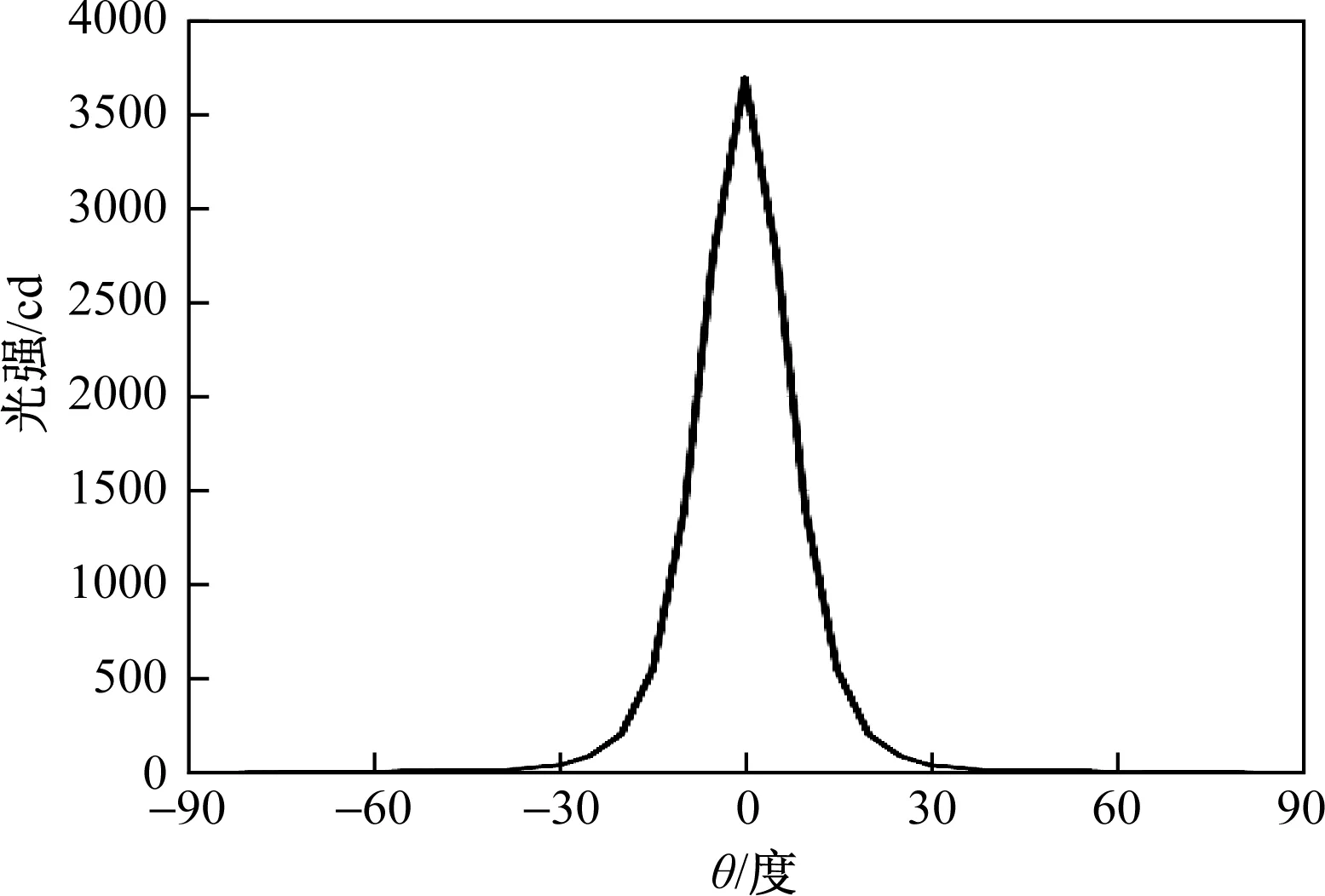
图7 验证实例4.4:LED射灯No.2的光分布Fig.7 Luminous intensity distribution of example 4.4:LED reflector lamp No.2

表4 实例分析与验证:LED射灯No.2Table 4 Result of example: LED reflector lamp No.2
4.5 LED筒灯No.1(见图8、表5)
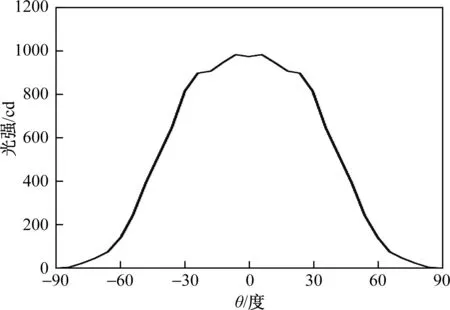
图8 验证实例4.5:LED筒灯No.1的光分布Fig.8 Luminous intensity distribution of example 4.5: LED downlight No.1

表5 实例分析与验证:LED筒灯No.1Table 5 Result of example: LED downlight No.1
4.6 LED筒灯No.2(见图9、表6)

图9 验证实例4.6:LED筒灯No.2的光分布Fig.9 Luminous intensity distribution of example 4.6: LED downlight No.2

表6 实例分析与验证:LED筒灯No.2Table 6 Result of example: LED downlight No.2
4.7 LED球泡灯(见图10、表7)

图10 验证实例4.7:LED球泡灯的光分布Fig.10 Luminous intensity distribution of example 4.7: LED bulb lamp

表7 实例分析与验证:LED球泡灯Table 7 Result of example: LED bulb lamp
5 结论
如果假定光强在球带上随θ角线性变化,则根据数学推理,应按改进后球带法的式(8)计算该球带的光通量。这样计算出的光通量相比旧球带法式(5)计算出的光通量误差小,理论分析(图3,式(9))第4节中的实例均证明了这一点。
据笔者的了解,在利用光强分布计算总光通量或部分光通量的实际应用中,仍多采取式(6)的求和方法进行(对非轴对称光源,先对光强在水平面上求平均,再利用此式),如本文的分析,在Δθ足够小的情况下(3°或更小),计算误差较小。但如果Δθ比较大(>5°),并且光强在垂直方向上变化较大时(例如射灯、筒灯等方向性光源),计算误差会较大。但无论如何,这种计算误差都是客观存在的。因此,笔者认为在高精度要求的场合,有必要对按式(5)计算造成的计算误差进行估算,如果误差较大,应按式(8)的算法进行修正。
更进一步,在所有要应用到球带光通量的场合,例如LM79-08、GB/T 29293—2012等标准中求平均色度时,都应该对按式(5)计算造成的计算误差进行评估,特别是在这两个标准中Δθ都为10°。
[1] 周太明,周详,蔡伟新.光源原理与设计[M].2版.上海:复旦大学出版社,2006.

