基于小波包降噪的地磁场干扰数据分析

徐斌， 顾伟

(上海海事大学 物流工程学院，上海 201306)

0 引 言

在现代海军发展中，测磁与消磁已经成为关系到舰艇生存的重要技术.港口消磁站的建设也已成为海军舰艇基地的重要项目.在港口消磁站测量的信号中除舰艇的磁场外还包含地磁场和其他环境或铁磁物质的信号，因此要进行信号分析降噪，才能准确地得到所需的磁场信号.

在现代地磁测量中，有不少可行的降噪方法在地震电磁检测站得到实际应用[1]，其中比较有效的为小波降噪算法.然而在现有的港口消磁站测磁环节研究中，还没有如何降噪的应用算法.

本文在研究小波算法与小波包算法[2]的异同和优点后，对消磁监测站测量的舰船磁场原始信号运用小波包降噪算法进行分析，分离出地磁日变干扰磁场及港口消磁站附近日常作业产生的干扰磁场，从而得到平稳的地磁测量信号.

1 测量实验平台

在港口测磁过程中采用磁通门传感器[3]阵列采集磁场信号.磁通门传感器利用材料的B-H饱和特性进行弱磁场测量，其测量范围在10-11～10-2T，能够有效捕捉极弱磁场的特征信号.在港口测磁过程中，磁通门采用多传感器(皆为三分量传感器)阵列方式，Z轴平行于地磁Z轴方向.

实际测量磁场存在干扰，因此需要进行数据处理滤除干扰磁场.

磁场实测值=被测对象磁场+人为干扰磁场+背景地磁场

人为干扰磁场=港口日常作业的干扰磁场+港口船只出入的信号瞬变干扰磁场

背景地磁场=本地地磁磁场+地磁日变磁场

地磁日变磁场基本可分为地磁每日都存在的地磁静日变化和地磁扰日变化,其中：地磁静日变化为具有周期性的连续磁场变化;地磁扰日变化为无周期性的随机磁场变化，不是恒定值.因此在实际测量中，将背景地磁场中的地磁日变磁场作为干扰量.本地地磁磁场为由地壳以下地核场、地壳场与本地周围固定建筑群的磁场之和，为测量时基本固定的本地环境磁场.因此，实际测量中的干扰磁场为人为干扰磁场与地磁日变磁场之和.

在实际测量中干扰信号一直存在，因此先对无舰船时的环境磁场进行测量和分析.在实际测量中对环境中的地磁日变磁场以及正常运行的港口附近高压电、电机等干扰磁场进行25 h不间断监测.数据由磁通门传感器阵列采集，采样时间自第一天10:40起至次日11:40结束，每分钟采样6次，得到磁通门传感器阵列磁场数据.

2 干扰磁场分析

2.1 地磁日变磁场

地磁日变磁场为一个太阳日中主要由固体地球外部原因引起的、叠加在地球基本磁场之上的各种短期的地磁变化.按照成因不同，变化磁场可分为平静变化和干扰变化两大类.[4]前者的基本成因是电离层在地磁场中运动产生较为稳定的电流体系;后者的基本成因是太阳风与地磁场相互作用，在磁层和电离层中形成各种短暂的电流体系.地球外部的各种电流体系，都能在固体地球内部感应出相应的内部电流体系.每一种地磁变化都是外部电流体系与内部电流体系产生的磁场之和,一般前者约占总和的70%，后者约占30%.静日变化Sq虽然依赖于当地太阳时, 并以一个太阳日为周期, 但它在时空分布特征上是有差异的, 而且纬度不同的地区静日变化规律不同.静日变化的日变曲线在形态上基本一致,白昼起伏大,夜间相对稳定,极大值和极小值主要出现在白天.扰日变化为无规律的随机磁场变化，虽然在地磁日变磁场中仅占小部分，即使在地磁活动十分平静期间，也或多或少地存在扰日变化.图1为测点附近地磁日变曲线示例，数据来源于测点附近地磁监测站公示的地磁日变采样数据，横坐标为测试地点的时间(当地时)轴，且对应的每3 h的Kp指数值均≤2.图中所示的磁场为：在测试地点周围区域存在铁磁性物质，但测试期间无铁磁性物质在附近移动及所在区域无强电供应的情况下测量得到的磁场.由Kp指数可以看出，图中所示测试时段内，测点附近的地磁变化的主要影响因素为静日变化,扰日变化虽然存在但相对较为平静.图中的磁场随时间进行着缓慢、平稳的变化，总体变化趋势具有一定的规律,短时变化为无规律的、幅值≤±10 nT的、随机变化的白噪声.

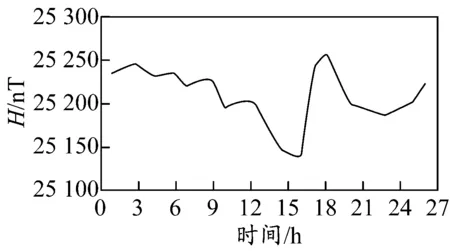
图1 测点附近地磁日变曲线示例

2.2 港口测磁点附近港口作业产生的干扰磁场

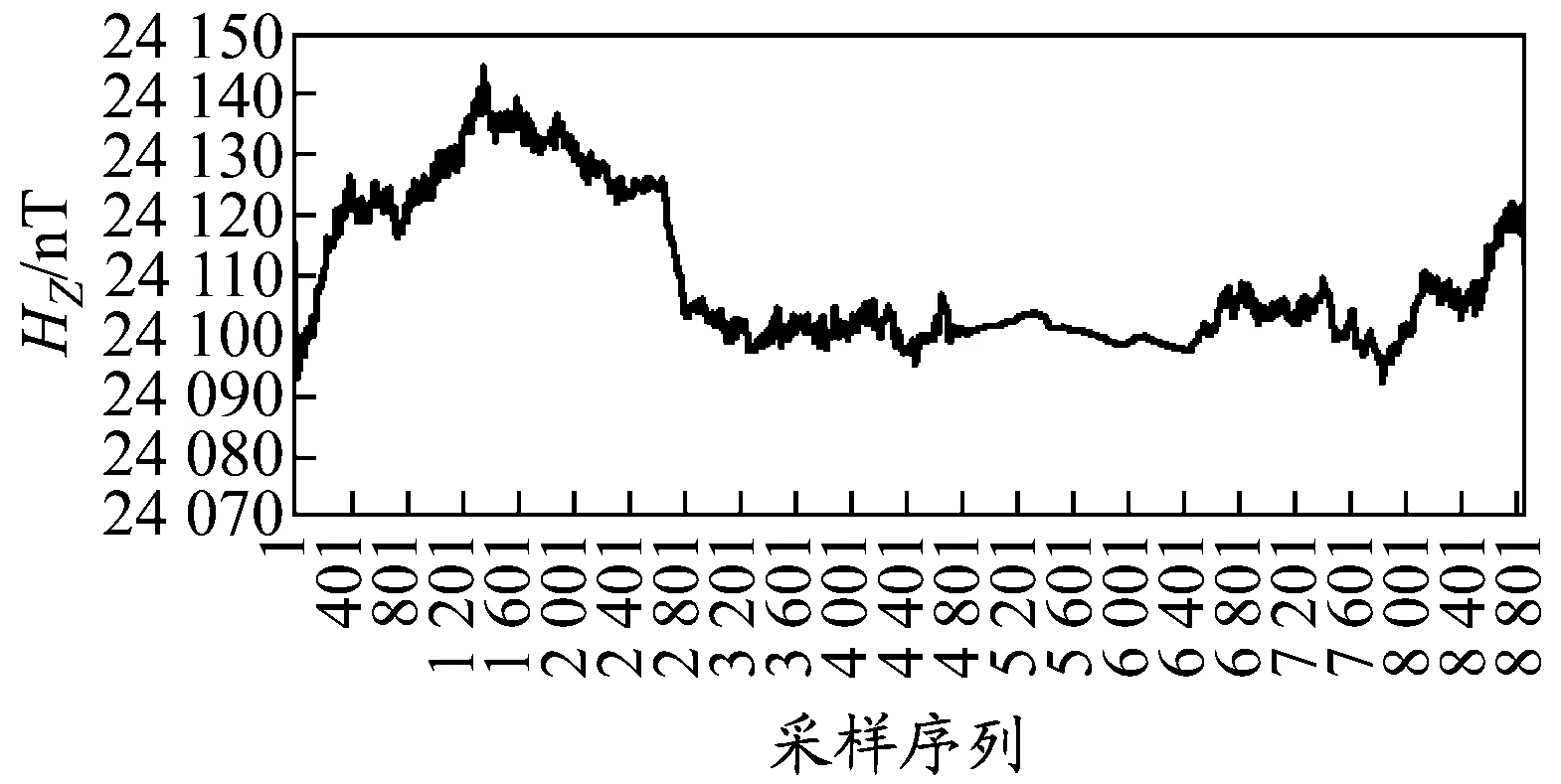
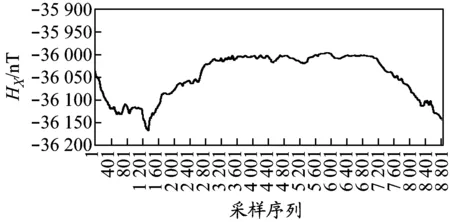
港口测磁点附近各种设施的运作所用的高压电由岸电供应.由港口作业大型机械、岸电供电站、岸电供电线路、港口行车轨道、大地形成电流回路.在港口行车轨道与大地不完全绝缘时，会造成电流部分泄漏.这部分泄漏电流本身会产生磁场且供电电路中电流不平衡会形成磁场.而磁传感器的安装位置离港口只有几公里，因此测量时会受到港口磁场的影响.图2为一组从早上10:40开始测量的25 h三分量磁场数据图，横坐标为采样序列，每分钟采样6次.从图中可以看出，在三分量磁传感器中，在上午10:40至午夜12:00磁场幅值波动强烈，虽然Z分量磁场还是依照日变曲线的变化规律浮动，但是其幅值振荡无规律，其振幅比午夜12:00至早上6:00扩大十几倍，X与Y分量受到附近电磁干扰影响较小.磁场变化特征符合日常港口作业时间特点.因此可以断定，消磁站附近的日常作业产生的电磁干扰是存在且明显的.

(a)X分量磁场

(b)Y分量磁场

(c)Z分量磁场

2.3 消磁站附近港口船只出入瞬变干扰

港口日常作业时，会不时有船只进出港.船只靠近磁传感器时势必会引起磁场的异变，其特征为瞬变、幅值大、时间短，在数据图上表现为一个突变峰值，很容易识别和抑制处理.在本次实验中，临时禁止任何船只进出港口，使港口船只出入引起的瞬变干扰得到完全抑制.

3 小波包降噪

3.1 小波包分析重构

小波包变换由小波变换发展而来，可以视为普通小波函数的线性组合.小波变换从空间(时间)和频率的局部变换中提取信号中有用的信息.[5]小波变换的本质是低通滤波,然而其直接滤除高频信号的特点会使一些有用的高频信号细节丢失.小波包变换在处理信号时同时分解高频与低频部分，因此更具有灵活性.因此，对含噪信号进行小波包变换，对其小波包系数进行阈值操作，然后进行重构，得到的消噪后信号优于小波变换的处理结果[6].

小波包降噪步骤为：信号的小波包分解、确定最佳小波包基、小波包分解系数的阈值量化、小波包信号重构.图3为小波包分解树，其中:S为原信号，f为信号频率，A代表低频段，D代表高频段.由图3可以看出，原信号S可以进行多层分解，直到其分解的小波包能够满足分析需求.第1层分解为尺度参数为1的互不重叠的高频D((fl+fh)/2,fh)与低频A(fl,(fl+fh)/2)两部分，原信号S的完整尺度(fl,fh)被分割.第2层分解得到尺度参数为2的4个频率范围AA(fl, (fl+fh)/4)，AD((fl+fh)/4, (fl+fh)/2)，DA((fl+fh)/2, 3(fl+fh)/4)，DD(3(fl+fh)/4,fh).如果进行n层分解，可以得到尺度参数为n的、2n个节点的小波包分解树.图3中进行的2层分解仅用于演示说明，实际分解层数需按信号计算得到最佳分解树才能确定.

图3 小波包分解树状图

信号以f(c)正交小波分解的公式[7]为

Pj-1f(t)=Pjf(t)+Djf(t)

(1)

(2)

(3)

小波包的重构公式为

(4)

3.2 阈值的选取

阈值如何选择、小波包系数如何进行阈值量化一直是小波包降噪算法核心中的核心，直接关系到信号去噪的品质.一般数据的数组序列中,xi=fi+ei(i=1,2,3,…,n),其中,fi为信号序列部分，ei为高斯噪声序列，且ei与fi互不相关.xi的性质可用它的小波包系数描述.小波包系数反映信号的能量，因此通常将小波包系数看作“能量元”，其系数大小代表其携带能量的多少.[8]噪声中信号信息的小波包系数值一般小于fi小波包系数值.噪声小波“能量元”在经过正交镜像滤波分解后，变成在整个小波包系数轴的均匀分布.[9]因此,可以选择一个阈值，滤除所有等于或小于阈值的小波包系数，保留所有大于阈值的小波包系数，用以重构信号.[10]在选取阈值的过程中，阈值太大不仅会滤除噪声信息而且会滤除有效的原有信号细节部分，使重构得到的信号损失部分特征甚至完全失真;阈值太小会使噪声信号得不到滤除，无法达到预期的降噪效果.[11]由此可见，不同阈值所形成的信噪比截然不同，因此阈值的选取至关重要，需在实验中不断尝试，得到最优阈值后再进行降噪处理.

小波包信号阈值去噪方法通常有：固定阈值、自适应阈值、混合型阈值和最小最大准则阈值.实际工程中，软阈值和硬阈值应用最多.[12]软阈值模型为

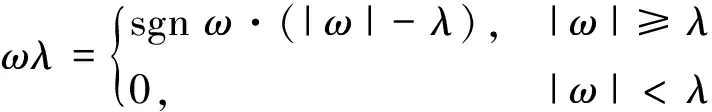
(5)

硬阈值模型为

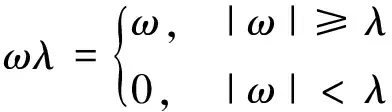
(6)

式中：λ为阈值；ω为原信号节点能量元.

本文采用一种新的阈值函数，并用MATLAB进行新阈值函数下的小波包信号去噪运算[13].

(7)

为衡量上述3种阈值消噪的效果，通常采用信噪比和均方差作为衡量标准.信噪比

(8)

均方差

(9)

式中:I和Id分别为原始信号和消噪后的信号.

表1 3种阈值消噪的θ和ρ

表1列出上述实验中降噪后信号的信噪比θ以及原始信号与消噪后的信号之间的均方差ρ.由表1可以看出，改进方案的降噪效果明显比单纯的软阈值或硬阈值方法好，从而验证改进方案的有效性.

3.3 小波包MATLAB实现

MATLAB小波包程序[14]如下：

>>save mag.mat S；%将地磁数据信号S存储在mag.mat文件中；

>>load mag；%将文件装载到matlab环境中；

>>S=A(1：8860)；%将信号的8860个数据给变量S；

>>wpt = wpdec(S,3,‘db1’, ‘user’) ；%使用db1小波包对S进行3层分解；

>>wpt = wpsplt(wpt,[3 0]); %分解小波包节点(3,0);

>>cfs = wpcoef(wpt,[3 0]); %读取小波包(3,0)的系数;

>> s130=wprcoef(wpt,[3,0]); %重构节点(3,0);

…

>> s137=wprcoef(wpt,[3,7]); %重构节点(3,7);

>> subtlot(311);tlot(a1);

上述程序中的S为对每个节点系数设置阈值后得到保留的有用系数.

4 数据处理结果

图4为采用软、硬阈值方法去噪后的Z分量磁场数据.图5为采用新阈值方法去噪后的三分量磁场数据.比较图4和5的Z分量数据可知，新阈值方法比普通软阈值和硬阈值方法降噪效率更好，能得到更好的信噪比.从图5可以看出，滤波后的信号在保持地磁的日变形态基本不变的同时，大幅降低由港口正常作业引起的电磁干扰幅度.图6为理想无干扰Z分量磁场数据图，数据来源于当日地磁站公示的日变磁场查表数据.从图5和6中可以得出，降噪处理后的数据基本符合理想实测数据，说明小波包降噪能在有效降噪的同时，比较完整地保留原始数据中的有效数据.图7为从处理后数据中任意截取的50 min地磁数据图.从图7中可以看出,地磁日变的白噪声可以控制在5 nT之内.因此可以得出结论：小波包降噪算法能够较为有效地抑制人为干扰,并且能对地磁日变干扰磁场起到一定的抑制效果.

(a) 软阈值方法

(b) 硬阈值方法

(a) X分量磁场

(b) Y分量磁场

(c) Z分量磁场

图6 理想状态下的Z分量磁场数据

图7 50 min磁场数据

5 结 论

小波包分解重构算法在实际应用中对港口正常作业所引起的干扰磁场的抑制效果比较明显，对测量舰艇信号，降低由地磁日变磁场、港口正常作业所引起的地磁干扰起到积极作用.不过小波包算法对信号进行降噪处理时计算量较大，具有一定的延迟，如何实现高度实时性还需在以后的研究中继续探索.

参考文献：

[1]刘宗尧. 地磁信号检测系统设计及误差补偿研究[D]. 南京: 南京理工大学, 2011.

[2]李凤阁, 李鹏. 基于小波和小波包的信号消噪方法分析[J]. 山西科技, 2010, 25(4): 70-73.

[3]郭爱煌. 磁通门技术及其应用[J]. 传感器技术, 2000, 19(4): 1-4.

[4]卞光浪, 边刚, 于波, 等. 基于多分辨率分析地磁日变信号去噪方法[C]//中国测绘学会第十八届海洋测绘综合性学术研讨会论文集. 2010: 66-68.

[5]韩朝晖. 利用小波包分析提取信号分量[C]//2006北京地区高校研究生学术交流会——通信与信息技术会议论文集(上). 2006: 582-589.

[6]MALLAT S G. A theory for multiresolution signal decomposition: the wavelet representation[J]. Pattern Anal & Machine Intelligence, IEEE Trans, 1989, 11(7): 674-693.

[7]ZHANG Xuming, XIONG Youlun. Impulse noise removal using directional difference based noise detector and adaptive weighted mean filter[J]. Signal Processing Letters, IEEE, 2009, 16(4): 295-298.

[8]CHUI C K, LIAN J. A study of orthonormal multi-wavelets[J]. Appl Numerical Math, 1996, 20(3): 273-298.

[9]任大男, 任韧. 自适应小波包正交性系统研究[J]. 应用光学, 2010, 31(S): 61-65.

[10]YUAN Jing, HE Zhengjia, ZI Yanyang,etal. Adaptive multiwavelets via two-scale similarity transforms for rotating machinery fault diagnosis[J]. Mech Systems & Signal Processing, 2009, 23(5): 1490-1508.

[11]孙洁娣, 靳世久. 基于小波包能量及高阶谱的特征提取方法[J]. 天津大学学报, 2010, 43(6): 562-566.

[12]鲁怀伟, 杜三山. 一种小波包去噪自适应阈值算法[J]. 兰州铁道学院学报: 自然科学版, 2001, 20(6): 11-15.

[13]曲国庆, 党亚民, 章传银, 等. 小波包消噪方法分析及改进[J]. 大地测量与地球动力学, 2008, 28(4): 102-106.

[14]王嘉梅. 基于MATLAB的小波包信号消噪处理[J]. 计算机与网络, 2001(1): 52-53.