电网中故障受分布式电源影响的分析

王双杰，杨炳元，高焱

(内蒙古工业大学 电力学院，内蒙古呼和浩特 010080)

0 引言

分布式电源的并网规模逐年扩大，分布式电源接入配电网改变了传统配电网单向放射状的网络拓扑结构，对配电网继电保护的灵敏性、选择性及重合闸均造成不同程度的影响［1－6］。

据统计，电网中发生的故障中电弧故障发生率超过80%［7］，所以在短路电流研究中有必要考虑电弧电阻的影响。故障电流的大小取决于电弧电阻值，而电弧电阻本身是故障电流的一个非线性函数，要精确计算出故障电流，首先要计算出电弧电阻值。传统故障电弧值计算方法有两种:一种是将电弧视作集中参数的电阻，在短路研究时用纯电阻来代替，故障电阻全凭经验来估算;另一种方法是进行简化，忽略故障电弧的存在，直接用求解短路问题的常规方法来解决问题［8］。显然，第二种方法中计算结果的正确性无法保证。

短路特性是保护配置的前提和依据，而影响配电网的故障特性的因素也随着分布式电源的接入而变得多样，因而有必要对这些因素进一步研究。

1 计算原理分析

本文采用了基于混合补偿法的配电网短路分析法。此方法把三相分布潮流的计结果作为故障前的状态［9］，更新混合电流注入值之后的结果作为故障后的状态。该方法需要创建一个故障戴维南等效阻抗矩阵，并结合循环断点补偿、分布式电源补偿和应用于协调相位的故障补偿三种补偿方法进行分析。

设单位长度的电弧电压为Ea，Ea表达式如下［10］:

由数据记录分析得出电弧电阻的公式如下［11］:

式中Ra是电弧电阻，单位是Ω;L是电弧长度，单位是m;If是电弧电流，单位是A;Ea单位长度电弧电压的单位是V/m。

将(1)式代入(2)式可得电弧电阻:

据(3)式可知电弧电阻是其电流的一个非线性函数，与电弧的长度成正比。在故障点构建电弧模型［12］，采用基于迭代混合补偿短路算法来构建非线性电弧电阻，通过迭代计算出短路电流和电弧电阻。迭代法求解步骤如下(k是迭代指数):

第一步:设电弧电阻的起始值为零，Ra(k=1)=0。

第二步:使用短路补偿法及在上面第k步中的电弧值，计算故障电流If(k=1)。

第三步:k=k+1。

第四步:利用(3)式和If(k)来计算电弧电阻Ra(k)。

第五步:更新的戴维南等效阻抗矩阵Zt，计算故障电流If。

图1 迭代流程图

上述的方法适用于现行的大多数的三线制、四线制中性点有效接地或不接地系统中压配电网。因为实际应用时变压器的不同配置和负载模型也影响短路电流值，所以要根据具体情况分析。

2 算例分析

在PSCAD/EMTDC中建立IEEE34节点网络仿真模型(如图2所示)。测试网络总消耗功率是1770 kW，负载集中在距供电网56 km处的连接点上。最远的节点距供电网59 km。网络在一个单一的电压水平下进行模拟。变电站69 kV/24.9 kV(Δ/Y)，低压侧接地，系统的等效系统阻抗为(5+j5)Ω/相。绕线转子异步风力发电机连接在节点23上，额定输出有功功率为300 kW，计算输入无功为134.5 kVar，输出电压25.1 kV，内阻Zw=(0.6+j1.5)Ω/相。设电弧长度 L=0.15 m。

图2 Ieee34节点示意图和PSCAD下的仿真模型

为了评估分布式电源对故障的影响、说明考虑电弧的必要性，本文主要做了两个仿真研究，考虑了位于配电网不同地点的几种常见故障类型。在第一个仿真中，没有分布式电源接入。在第二个仿真中，分布式电源由节点23并入电网。仿真中忽略了接地电阻，对于相间故障和两相接地故障，分别测量两个故障相的故障电流值并利用(3)式计算电弧电阻值，对于三相接地故障，测量三相电流值并利用(3)式计算三个电弧电阻值，将最后结果导出，作图比较，如图3所示。

图3 分布式电源接入前后30节点三相接地故障电流值

图3所示为分布式电源接入前后30节点三相接地故障电流值。分布式电源的接入节点23后，显著提高了故障电流水平。如图4所示，在分布式电源接入前后的测试网络发生单相接地故障和三相接地故障时的电弧电阻。结果显示，分布式电源加剧了配电网的故障水平，电弧电阻值比之前变小了。相间故障和两相接地故障情况与上述情况类似。当故障发生在分布式电源接入点和邻近的节点上时，故障电流水平的提高非常显著，使得电弧电阻降低。改变分布式电源的接入位置，故障电流也将随之改变，同时影响电弧电阻值。

图4 单相接地和三相接地故障时的电弧电阻值

在测试网络的分析中，当分布式电源接点远离变电站时，三相和单相短路的故障电流水平显著增加。电弧电阻计算值在0.4～2.5Ω之间。远离变电所发生单相接地故障，电弧电阻达到最大值。

设没有分布式电源接入的配电网电弧电阻Ra和有分布式电源接入时的配电网电弧电阻Rag之间的差异为ΔRa的值代表了分布式电源对不同节点相接地故障的电弧电阻的影响，如图5所示。在馈线的末端ΔRa达到最大值，即在馈线的末端发生故障时，分布式电源对电弧故障的影响最大。

图5 单相接地故障时分布式电源对电弧电阻的影响

由于忽略了电弧，而造成故障电流计算的误差表达式如下:

其中If0是忽略电弧的情况下，馈电网顶端的故障电流。Ifarc是考虑电弧的情况下电网顶端的故障电流。

图6显示了根据式(4)计算的误差值。没有分布式电源接入时，由于忽略电弧，故障电流的计算误差范围为2～12.2%。在馈电线路末端发生单相接地故障时，误差最大。

3 线路中电弧故障的影响因素分析

将仿真中的绕线转子异步风力发电机换双馈异步风力发电机，额定功率和额定电压相同时，同样在30节点处测得的故障电流如图7所示。

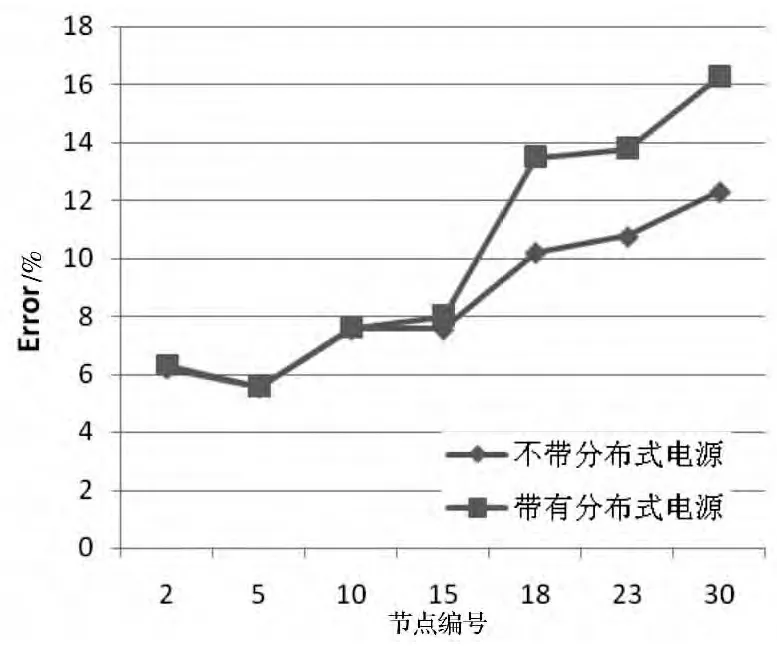
图6 单相接地故障时故障电流计算误差

图7 30节点在不同种类分布式电源下三相接地故障电流值(左图绕线异步风机情况下，右图为双馈机情况下)

双馈风力发电机与绕线异步风力发电机不同，绕线异步风力发电机定子直接接入电网，发电机在输出有功的同时还要向电网吸收无功，补偿期间异步发电机励磁电流减小，发电机输出故障电流能力下降;双馈异步风力发电机定子侧接入电网，转子侧采用三相对称绕组，经背对背PWM(脉宽调制)双向变流器接入电网，为转子提供不间断的交流励磁电流。

除了风力发电机的类型能够影响故障处的响应特性外，风机所处位置的风速也会影响故障点电流。如图8所示，表示在其他条件相同时，不同风速下故障电流的比较。

图8 不同风速时30节点三相接地故障电流值(左图风速为4 m/s时，右图风速为12 m/s)

影响带有分布式电源的配电网中故障特性的因素还有很多，比如故障类型、故障点位置、并网控制方式等。此外，故障切除后，不同条件下风力发电机的电压恢复能力不同，这使得故障特性呈现出多样性。为了确保分布式电源并网后配电网的安全性，有必要对接入分布式电源后的配电网在发生故障后的不同故障特性进一步研究。由于篇幅所限，这里不一一分析了。

4 结束语

分布式电源显著提升了对所有类型故障的故障电流水平，尤其是在分布式电源接入点或邻近节点发生故障，使电弧电阻减小的情况下。而分布式电源增大了故障电流，降低了电弧电阻，降低了电弧对保护装置测量阻抗的影响。影响分布式电源故障特性的因素有多种，发电机种类、发电机原动机所处状态等都是重要因素，在分析带有分布式电源的配电网故障时有必要根据具体情况详细分析。

［1］ 孙景钌，李永丽，李盛伟，等.含逆变型分布式电源配电网自适应电流速断保护［J］. 电力系统自动化，2009，33(14):71－76.

［2］ Jenkins，N.Allan，R.Croslsey，P，Kirschen，D.Strbac，G:‘Embedded generation’ ［M］.London.The Institution of Engineeing and Technology，2000.

［3］ 林霞，陆于平，王联合.分布式发电条件下的新型电流保护方案［J］. 电力系统自动化，2008，32(20):50－56.

［4］ 李晓晖.分布式电源对配电网继电保护影响的研究［D］.北京:华北电力大学，2011.

［5］ 宋凯.考虑分布式电源接入的城区配电网保护研究［D］.上海:上海交通大学，2011.

［6］ 唐亮.分布式电源的分类及对配电网的影响［D］.合肥:合肥工业大学，2008.

［7］ Maikapar，A.S.Extinction of an open electric arc［J］.Elektrichestvo ，1960，4:64 －69.

［8］ Ciric，R.M.，Ochoa，L.F.，Feltrin，A.P.Nouri，H.:Fault analysis in four－wire distribution systems'［J］.IEE Proc.Gener.Transm.Distrib.2005，(12):977－982.

［9］ Cheng，C.S.，Shirmohammadi，D.:A three－phase power flow method for real－time distribution system analysis'［J］.IEEE Trans.Power Syst.1995，10(2):671 －769.

［10］ Goda，Y.Iwata，M.，Ireda，K.Tanaka，S.:Arc voltage characteristics of high current fault arcs in long gaps'［J］.IEEE Trans.Power Deliv.2000，15(2):791－795.

［11］ Terzija，V.Koglin，H.J.:‘On themodelling of long arc in still air and arc resistance calculation’［J］.IEEE Trans.Power Deliv，2004，19(3):1012－1017.

［12］ Terzija，V.V.Ciric，R.M.，Nouri，H.:‘A new iterative method for fault current calculation which models arc resistance at the fault location’［J］.Electr.Eng.2006，89(2)，pp.157－165.