基于非惯性系的悬停状态旋翼CFD／CSD耦合气动分析

肖 宇，徐国华，招启军

（南京航空航天大学 直升机旋翼动力学国家级重点实验室，江苏 南京 210016）

0 引 言

随着直升机技术的发展，传统的基于升力线理论的气动模型已渐渐无法满足直升机旋翼空气动力学精细化分析的要求，因此高精度的CFD技术逐渐被应用到旋翼气动分析中。而早期的旋翼CFD分析中，考虑到计算效率等问题，在处理旋翼桨叶时，大都采用了刚性桨叶假设［1］。但是对于具有大展弦比的柔性桨叶来说，旋翼旋转时桨叶气动弹性效应明显，特别是具有先进气动外形的旋翼气弹耦合特性更复杂，只有在CFD分析中考虑旋翼的弹性变形影响才能更准确地模拟旋翼流场及气动载荷特性。为了更好地与CFD方法的分析精度相匹配，弹性旋翼的变形一般采用基于有限元法的CSD计算得到。当前CFD／CSD的耦合分析已逐渐成为直升机旋翼气动分析的最新研究热点［1－3］。

1986年，Tung等人最早进行了直升机旋翼的CFD／CSD的耦合计算，其中CFD部分采用小扰动方程计算［4］，随后将之改进为基于全位势方程的CFD方法［5］，但在该模型中，需要从CSD模块提供入流角，通过修正物面无穿透条件来代替网格变形，同时入流角也考虑了CFD计算域外尾迹的影响。此外，采用该处理方式导致早期的CFD计算精度不足，在进行耦合时存在着收敛性问题［6］。随着CFD计算方法和计算机性能的发展，基于Euler和N－S方程的CFD慢慢进入到耦合计算中，现在发展到采用基于嵌套网格的CFD计算与CSD计算相耦合的阶段，可以直接模拟背景流场和所有的旋翼桨叶流场特性，避免了早期耦合所需的入流角修正处理，如Potsdam等人的研究工作［7］。另外，Datta等人采用了基于单桨叶的混合CFD方法进行流固耦合计算［8］，对UH－60A直升机旋翼的气动和结构载荷进行了预测，同样取得了成功，该方法虽然计算效率高，但是其中自由尾迹方法存在某些经验参数，且不能准确模拟粘性效应，这会对气动特性计算精度构成一定的影响。国内在旋翼CFD／CSD耦合方面的研究开展的相对较晚，最近王海［9］、徐广［10］等人尝试进行了相关研究，获得了一些初步经验和结果。与此同时，国内外旋翼CFD／CSD耦合方法主要偏重于在惯性坐标系下建立分析模型，适合于前飞状态的耦合计算，但对于悬停状态情况，该方法的效率相对较低。

本文尝试在改进原有的旋翼CFD分析及旋翼CSD模型基础上，在非惯性系下将两者进行耦合开展分析计算，并考虑粘性的影响，建立一套适合于悬停状态弹性旋翼气动载荷分析的高效方法，随后将之应用到先进UH－60A直升机旋翼的悬停状态气动载荷分析中，获得了一些有实际价值的结果。

1 旋翼CFD计算模型

1.1 计算网格

计算网格采用嵌套网格系统，整个网格系统分为两大部分：一是包含弹性桨叶的贴体网格，二是包含整个计算流场域的背景网格。桨叶贴体网格采用C－H型网格，用来计及旋翼桨叶的刚性运动及弹性变形，背景网格则采用O－H型网格，用来捕捉旋翼远场尾迹［11］。

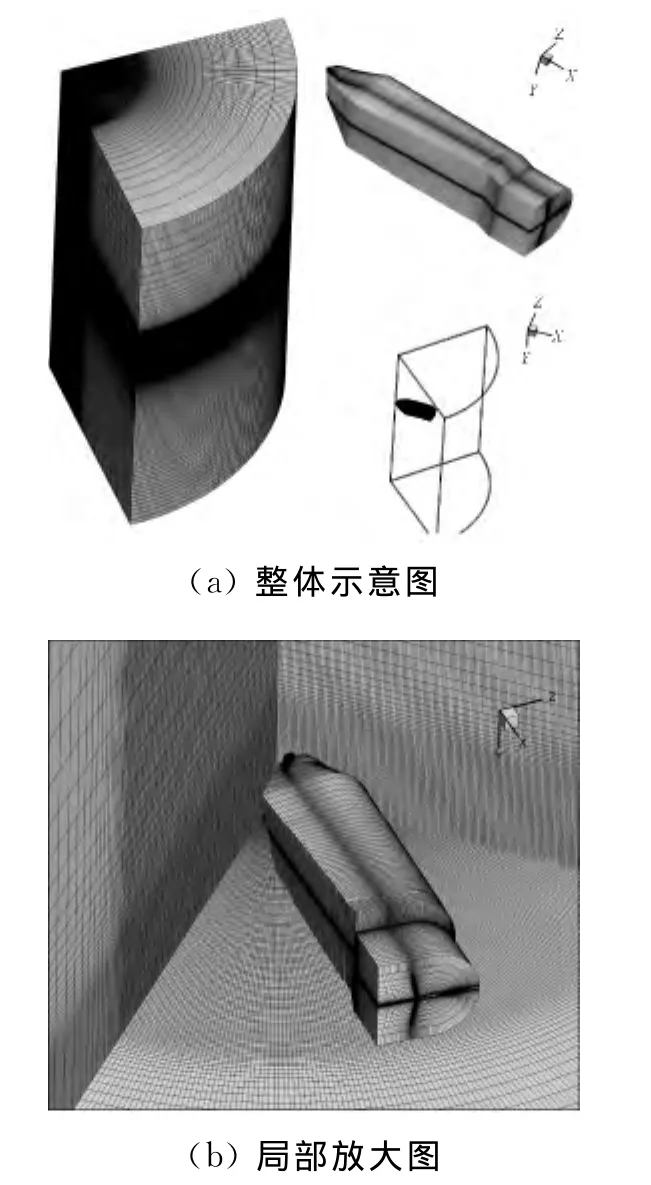
图1 旋翼流场计算网格系统Fig.1 Grid system for predicting the flowfield of rotor

图1为本文计算UH－60A旋翼悬停状态采用的嵌套网格系统示意图，旋翼贴体网格维数为177×44×104（弦向×法向×展向）；而背景网格维数为151×249×185（周向×轴向×径向）。由于桨叶网格需要捕捉物面的粘性流动，因此使用N－S方程求解，其第一层网格距物面距离为2.0×10－6c（c为桨叶弦长），而背景网格一般只需捕捉旋翼尾迹，从计算效率上考虑，采用Euler方程进行求解，选取的网格尺度相对较大，仅在桨叶旋转平面及尾迹区进行了加密，最密处网格尺度为0.1c。网格范围周向为±3R，轴向范围为－3.3R到2R，径向范围为0到3R，其中R为桨叶半径。嵌套网格中的贡献单元搜寻和信息传递采用了文献［12］的方法进行。

为了与CSD相耦合，桨叶网格需要进行动态变形，弹簧法虽然生成网格质量较高，但是计算需要迭代［9］，耗时较长，因此本文采用代数法进行网格坐标转换，从而实现网格变形［13］。该方法变形后网格可直接通过对变形前网格坐标的矩阵运算得到，无需迭代，具有较高的效率，便于CFD／CSD的耦合运算。

1.2 控制方程

针对直升机悬停状态，在旋转坐标系下建立控制方程，此时流场可视为准定常状态，其具体形式可以表达为：

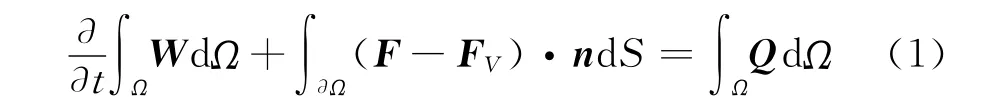
式中，W 为守恒变量，表达式为 ［ρ ρV ρE ］T，绝对速度V ＝ ［u v w ］T，n为单元法矢，ρ、p和E 分别为密度、压强和总能。对流通量F表达式为［ρV·n ρV（V·n）＋p·n ρE（V·n）＋pV·n ］T，FV为粘性通量。相对惯性系下的控制方程，非惯性系下附加了一个由于旋转产生的源项Q＝［0 －ρΩ×V0］T。

空间离散采用Jameson中心差分格式，时间离散格式则采用显式Runge－Kutta积分求解。另外采取了当地时间步长、隐式残值光顺和并行计算等加速收敛措施。

2 旋翼CSD计算模型

在直升机综合分析平台中，旋翼CSD计算模型一般采用二维线性截面分析结合一维非线性梁分析构成，如图2所示，这是为了在保证分析精度的同时，避免直接处理三维非线性有限元而造成的时间和内存的浪费，本文同样选用该方法构建旋翼结构计算模型。

2.1 截面分析模型

本文截面分析模型采用基于二维有限元的分析方法［14］，与早期解析法相比，有限元法能处理各种截面且无需做任何假设，因此得到广泛的应用。本文有限元单元采用四边形单元和三角形单元两种，分别采用Gauss积分和Hammer积分进行处理。图3给出了本文截面分析的有限元网格示意图。

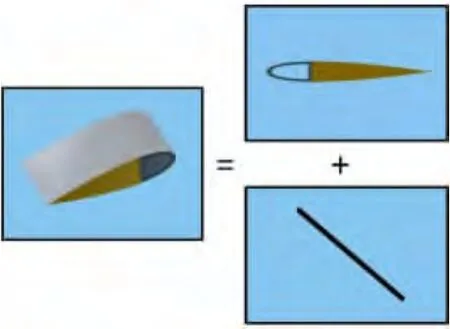
图2 旋翼CSD计算模型分解示意图Fig.2 Decomposition diagram of the blade CSD model

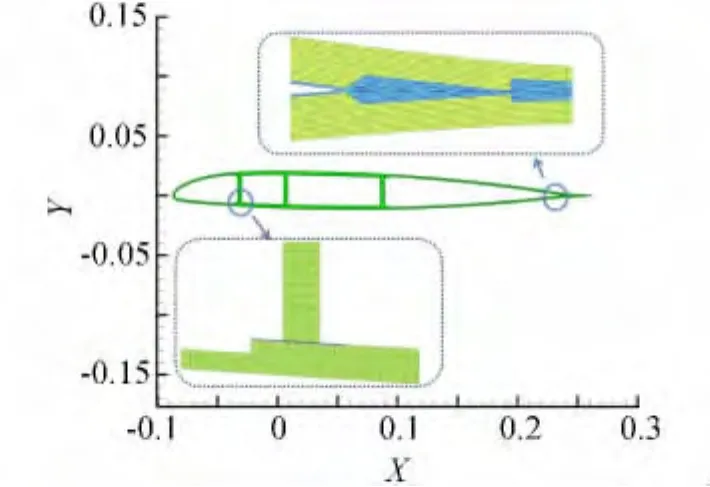
图3 截面示意图Fig.3 Schematic diagram of cross section

2.2 一维梁分析模型

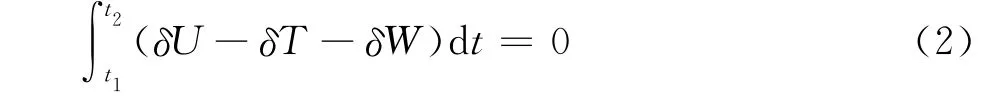
从哈密尔顿原理出发建立桨叶动力学方程：对于旋翼桨叶，式中δU、δT和δW 分别表示桨叶在某一状态的应变能、动能的变分和气动外力所做的虚功。对于有限元空间离散，本文选用基于中等变形梁理论的改进的YF模型进行［15］。原始的YF模型为23自由度，采用了基于圣维南原理的截面分析模块，具有一定的局限性。本文在此基础上，为了更好的与本文采用的截面分析模型相结合，对YF模型的自由度进行了精简改进，针对欧拉梁自由度数缩减为14，从而更有针对性的处理桨叶模型。图4为本文采用的欧拉梁模型自由度示意图。

图4 欧拉梁模型14自由度示意图Fig.4 Schematic diagram of Euler 14DOF beam model

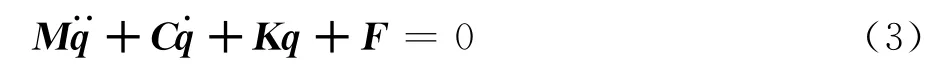
经过梁单元离散后即可得到描述一维梁动力学模型的非线性常微分方程组式：其中，M、C、K矩阵分别是质量、阻尼和刚度矩阵，F为桨叶所受的外力矢量，q为节点变形位移矢量。对于悬停状态的分析，式（3）可以简化为如下非线性代数方程，采用Raphson迭代法求解便可得到稳态的桨叶变形。

3 耦合策略

耦合旋翼CSD模型和CFD模型的关键在于如何进行两者信息的交换，由于实际耦合中结构模型桨叶采用一维梁单元模拟，而流场计算桨叶采用三维单元模拟，因此需要对两者交换的信息进行处理匹配后才能实现耦合计算。在实际计算中，流场模块对桨叶表面力进行弦向积分后等效至翼型1／4弦线处，将1／4弦线处的力和力矩传递给结构模块；而结构模块传递1／4弦线处的弹性位移，通过假设截面不发生弹性变形可以得到变形后的翼型点坐标，从而得到流场计算所需的网格信息。图5详细给出了本文建立的基于非惯性系的悬停旋翼CFD／CSD计算流程图，具体耦合分析步骤阐述如下：

（1）采用简单入流模型，对旋翼CSD模块进行初始化计算，获得桨叶稳态变形量；

（2）采用桨叶变形量对刚性桨叶贴体网格进行变形，建立旋翼CFD计算所需嵌套网格系统，并确定嵌套网格洞边界和贡献单元；

（3）进行旋翼CFD计算，收敛后计算桨叶表面的气动力分布；

（4）将CFD计算得到的气动力传递到旋翼CSD分析模块中，计算收敛后，获得较为精确的桨叶结构变形量；

（5）转到第（2）步重新开始计算，直到计算收敛为止。

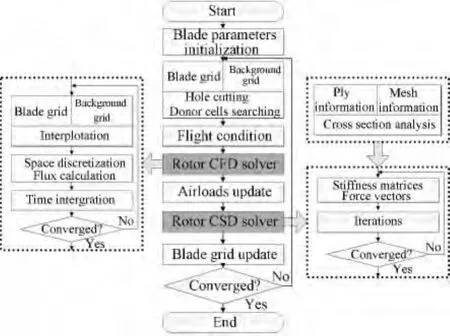
图5 悬停状态旋翼流场／结构耦合计算流程图Fig.5 Flow chart of CFD／CSD coupling for hovering rotor

4 算例结果

4.1 CFD验证结果

为了验证本文基于非惯性系建立的悬停状态旋翼CFD分析方法的正确性，采用有实验结果可供对比的美国NASA“Caradonna ＆Tung”模型旋翼［16］，该旋翼由于有详细的桨叶表面压力测量值而被广泛用于刚性旋翼CFD的验证中。其桨叶展弦比为6，翼型为NACA0012，桨叶无扭转和尖削。本文选取的计算状态为桨距8°、桨尖马赫数0.794这一跨音速算例。从图6中可以看出，本文的计算值与实验值吻合的相对较好，从图7中可以明显看出旋翼悬停状态尾迹边界的收缩，综上表明本文建立的基于非惯性系的悬停状态旋翼CFD计算方法的有效性和可靠性。

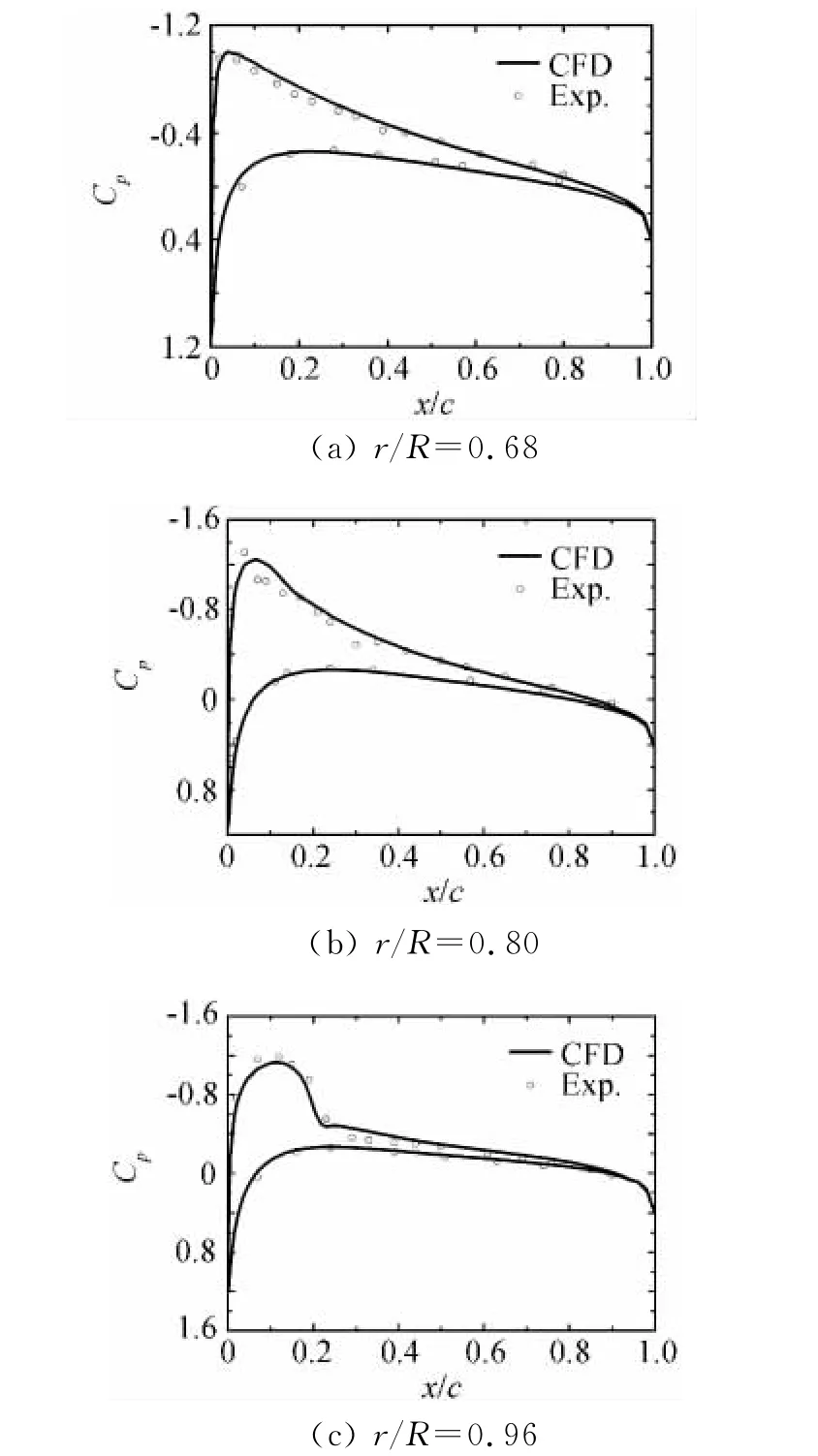
图6 Caradonna ＆Tung旋翼桨叶表面压强分布对比Fig.6 Surface pressure coefficients for Caradonna ＆Tung rotor

4.2 CSD验证结果

结构分析模型采用马里兰大学进行的旋转梁频率实验结果进行对比分析［17］。该实验详细记录了桨尖后掠角度对旋翼频率的影响，因此能够很有效的对结构分析模型进行校核。实验中分别测试了复合材料桨叶和铝合金桨叶，为了有针对性的验证本文后掠桨尖模拟的正确性，采用铝合金桨叶进行验证，实验在真空中进行，旋翼转速分别为0、500rpm和750rpm，桨尖后掠分别为0°、15°、30°和45°。文献中未给出材料属性，本文计算时假定模型由7075铝组成，具体模型几何及结构参数如表1所示。

图7 Caradonna ＆Tung旋翼涡量等值面图Fig.7 Iso－surface of vorticity for Caradonna ＆ Tung rotor

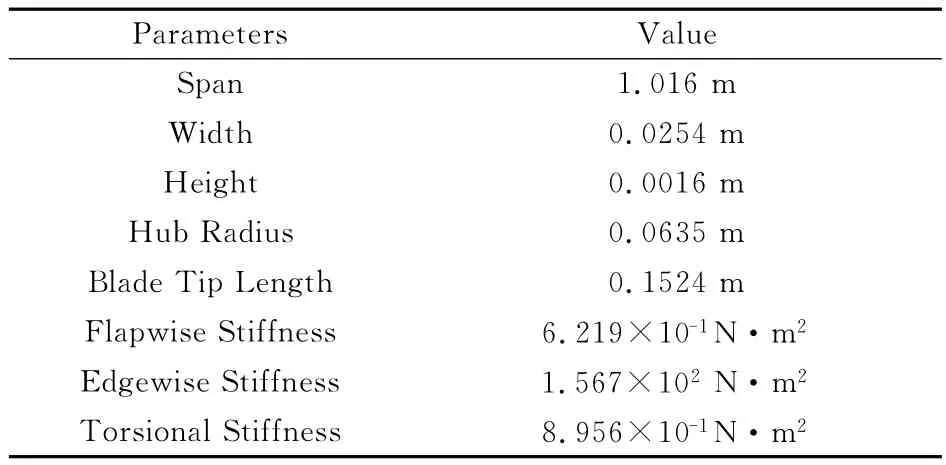
表1 旋转梁实验模型参数Table1 Parameters of experimental rotating beam

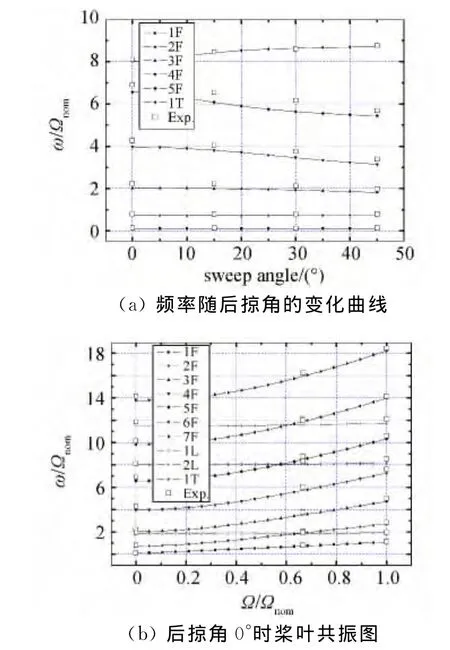
图8 旋转梁计算与实验结果对比Fig.8 Comparisons of the calculated results with experimental data for rotating beam

图8（a）显示了频率随后掠角的变化曲线，从图中可以看出，第一阶扭转频率随着后掠角度增大而增大，而高阶挥舞频率随后掠角度增大而减小。图8（b）为后掠角0°时的旋翼共振图，从中可以看出计算值与实验值吻合的相对较好，表明本文建立的结构模型可以有效地模拟带有后掠桨尖的先进旋翼结构动力学特性，为CFD／CSD耦合分析的结构模型提供良好基础。

4.3 CFD／CSD耦合计算结果

采用先进UH－60A直升机的模型旋翼的悬停实验作为CFD／CSD耦合验证算例［18］，该旋翼具有现代先进直升机桨叶的气动外形特征，主要特点有变翼型的布置、非线性负扭转分布和新型后掠桨尖等。旋翼桨叶采用21段Euler梁单元模拟，表2给出了本文计算的前八阶频率计算值和文献［19］计算值，从表中可以看出，对变形影响最大的一阶模态频率计算与文献参考值基本一致。

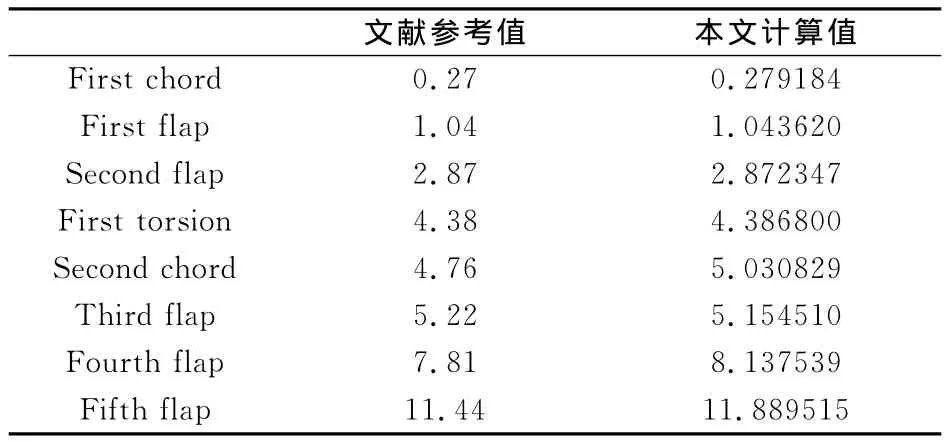
表2 UH－60A旋转桨叶频率计算结果Table2 Calculated frequency of UH－60Arotating blade

图9给出了本文弹性变形前后计算所用的网格，从图中可以明显看出桨叶的弹性变形，图10则给出了刚性旋翼CFD计算和CFD／CSD耦合计算得到的桨叶表面的压强等值线对比图。

图9 弹性变形前后计算网格示意图Fig.9 Schematic diagram of grid deformation

图11给出了刚性旋翼CFD方法和弹性旋翼CFD计算得到的表面压强系数分布与实验值的对比，从图中可以看出，在桨叶内侧剖面，两种方法的计算结果均与实验值吻合良好。考虑弹性影响的CFD／CSD耦合计算结果在桨叶外侧相对刚性计算值有所改善，表明CFD／CSD耦合后的分析方法有效地提高了对旋翼流场的模拟精度。

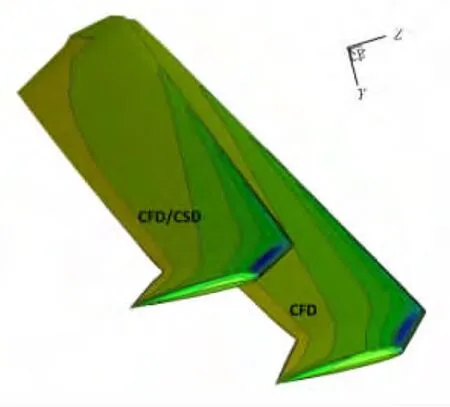
图10 UH－60A旋翼刚性／弹性桨叶表面压强等值线对比Fig.10 Comparisons of the surface pressure contour line for the UH－60Arigid／elastic rotor

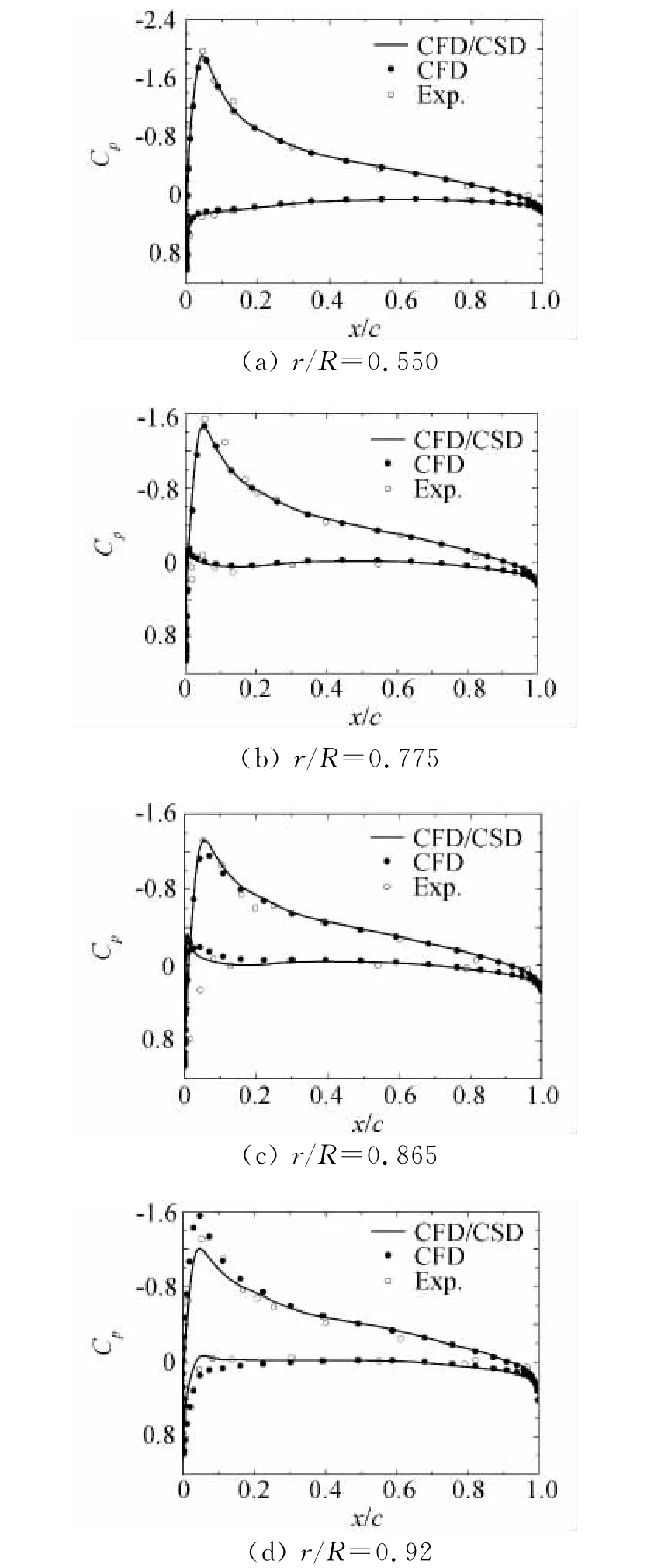
图11 UH－60A旋翼刚性／弹性桨叶表面压强系数分布Fig.11 Surface pressure coefficients for UH－60Arigid／elastic rotor

图12给出了刚性旋翼CFD和弹性旋翼CFD计算得到的桨叶展向剖面拉力系数分布与实验值的对比。由图可知，在桨叶内段大部分区域，计入桨叶弹性变形与否对桨叶剖面拉力分布的影响很小，但在靠近桨尖的区域，弹性旋翼CFD／CSD耦合计算和刚性旋翼CFD计算结果相比，与实验值吻合的要稍好，这是由于前者计算考虑了真实旋翼运动中存在的弹性挥舞及扭转变形，而后者会直接影响迎角。

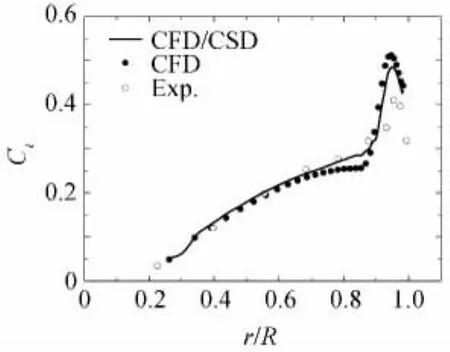
图12 UH－60A旋翼刚性／弹性桨叶剖面拉力系数分布Fig.12 Sectional blade thrust coefficient for UH－60Arigid／elastic rotor

除计算桨叶展向拉力分布外，本文还给出了耦合方法计算得到的UH－60A旋翼悬停效率与实验值的对比，如表3所示。从表中可以看出，本文建立的耦合分析方法可以有效的分析旋翼的悬停效率。

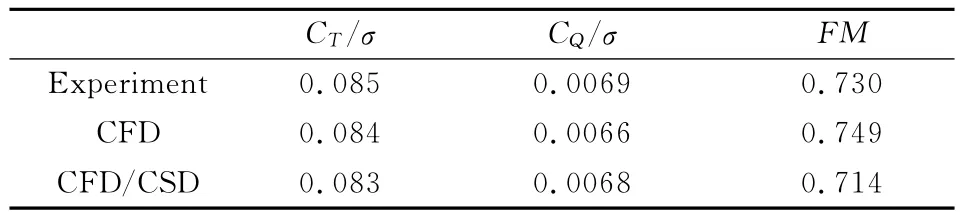
表3 UH－60A旋翼悬停效率计算值与实验值对比Table3 Comparisons of the calculated figure of Merit with experimental data for UH－60Arotor

图13给出了本文进行悬停弹性旋翼CFD／CSD耦合计算的收敛曲线。从图中可以直观的看出拉力系数CT、扭矩系数CQ及悬停效率FM 误差百分比的收敛过程。对于该算例，本文建立的模型最少经过三次迭代后即可得到较为满意的结果。综上计算分析结果表明本文的耦合方法能够用于具有先进气动外形的悬停状态直升机旋翼流场、拉力及性能等的计算。为进一步开展前飞状态下的直升机旋翼CFD／CSD耦合计算奠定基础。

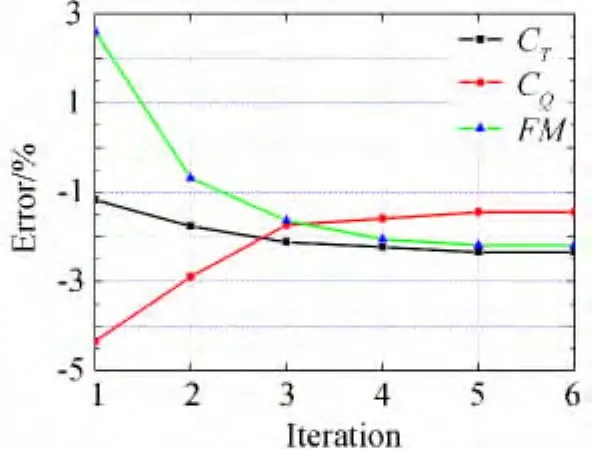
图13 UH－60A旋翼CFD／CSD迭代收敛曲线Fig.13 Convergence curve of CFD／CSD iteration for UH－60Arotor

5 结 论

本文建立了一个适合于悬停状态的旋翼CFD／CSD耦合分析方法，其中旋翼CFD部分采用求解非惯性系下N－S方程进行，而CSD模块则对三维桨叶进行解耦分解为二维线性截面分析和一维非线性梁分析。采用本文建立的耦合分析方法用于先进旋翼的悬停状态下的气动特性计算中，得到以下结论：

（1）本文建立的基于非惯性系的旋翼CFD／CSD耦合分析方法可以有效地用于悬停状态旋翼的气动载荷分析，基于本文耦合方法的弹性旋翼CFD计算结果相对传统刚性旋翼CFD计算更加可靠，与实验值更为吻合。

（2）相对弹簧法进行动态网格变形，本文采用的代数法具有效率高、鲁棒性好等优点，适合旋翼CFD／CSD的耦合计算。

（3）对于悬停旋翼CFD气动计算，考虑弹性进行分析得到的结果与刚性旋翼CFD结果在桨尖处区别明显，因此对于带有新型桨尖的旋翼气动分析，CFD／CSD耦合计算更能描述该桨尖的气动特征，体现出新型桨尖的优势，同时也表明直升机旋翼先进气动外形设计需要采用CFD／CSD耦合的分析方法。

［1］DATTA A，NIXON M，CHOPRA I.Review of rotor loads prediction with the emergence of rotorcraft CFD［J］.Journal of the American Helicopter Society，2007，52（4）：287－317.

［2］THOMAS S，ANANTHAN S，BAEDER J D.Wake－coupling CFD－CSD analysis of helicopter rotors in steady and maneuvering flight conditions［C］.Proceedings of the 68th Annual Forum of the American Helicopter Society，Ft.Worth，TX，May 1－3，2012.

［3］BIEDRON R T，Lee－RAUSC E M.Computation of UH－60A airloads using CFD／CSD coupling on unstructured meshes［C］.Proceedings of the 67th Annual Forum of the American Helicopter Society，Virginia Beach，VA，May 3－5，2011.

［4］TUNG C，CARADONNA F X，JOHNSON W.The prediction of transonic flows on an advancing rotor［J］.Journal of the A－merican Helicopter Society，1986，32（7）：4－9.

［5］STRAWN R C，TUNG C.Prediction of unsteady transonic rotor loads with a full－potential rotor code［C］.Proceedings of the 43rd Annual Forum of the American Helicopter Society，St.Louis，MO，May 18－20，1987.

［6］STRAWN R C，DESOPPER A，MILLER J，et al.Correlation of Puma airloads evaluation of CFD prediction methods［C］，Proceedings of the 14th European Rotorcraft Forum，Amsterdam，The Netherlands，September，1989.

［7］POTSDAMM，YEO H，JOHNSON W.Rotor airloads prediction using loose aerodynamic／structural coupling［C］／／Proceedings of the 60th Annual Forum of the American Helicopter Society，Baltimore，MD，June 7－10，2004.

［8］DATTA A，SITARAMAN J，CHOPRA I，et al.Analysis refinements for prediction of rotor vibratory loads in high－speed forward flight［C］.Proceedings of the 60th Annual Forum of the American Helicopter Society，Baltimore， MD，June 7－10，2004.

［9］WANG H，XU G H.Grid deformation method for flowfield simulation of elastic helicopter rotors［J］.Journal of Nanjing University of Aeronautics ＆ Astronautics，2011，43（1）：1－6.（in Chinese）王海，徐国华.用于弹性旋翼流场模拟的网格变形方法［J］.南京航空航天大学学报，2011，43（1）：1－6.

［10］XU G.Numerical simulation on aerodynamic characteristics of elastic rotor with new tip shape by N－S equations［D］.Nanjing University of Aeronautics ＆ Astronautics，2010.（in Chinese）徐广.新型桨尖弹性旋翼气动特性的Navier－Stokes方程数值模拟［D］.南京航空航天大学，2010.

［11］XU G，ZHAO Q J，WANG B，et al.Prediction on aerodynamic performance of advanced helicopter rotor in hover［J］.Acta Aeronautica et Astronautica Sinica，2010，31（9）：1723－1732.（in Chinese）徐广，招启军，王博，徐国华，高延达.先进直升机旋翼悬停状态气动性能计算［J］.航空学报，2010，31（9）：1723－1732.

［12］ZHAO Q J，XU G H.Grid generation technique for helicopter rotor CFD including blade motions［J］.Journal of Nanjing Uni－versity of Aeronautics ＆ Astronautics，2004，36（3）：288－293..（in Chinese）招启军，徐国华.计入桨叶运动的旋翼CFD网格设计技术［J］.南京航空航天大学学报，2004，36（3）：288－293.

［13］DATTA A，SITARAMAN J，CHOPRA I.CFD／CSD prediction of rotor vibratory loads in high－speed flight［J］.Journal of Aircraft，2006，43（6）：1698－1709.

［14］KOSMATKA J B.On the behavior of pretwisted beams with irregular cross－sections［J］.Journal of Applied Mechanics，1992，59（1）：146–152.

［15］FRIEDMANN P P，YUAN K A，DE TERLIZZI M.An aeroelastic model for composite rotor blades with straight and swept tips.Part I：aeroelastic stability in hover［J］.International Journal of Non－linear Mechanics，2002，37（4－5）：967－986.

［16］CARADONNA F X，LAUB B G，TUNG C.An experimental investigation of the parallel blade－vortex interaction［R］.NASA TM－86005，1984.

［17］EPPS J J，CHANDRA R.The natural frequencies of rotating composite beams with tip sweep［J］.Journal of the American Helicopter Society，1996，41（1）：29－36.

［18］LORBER P F，STAUTER R C，LANDGREBE A J.A comprehensive hover test of the airloads and airflow of anextensively instrumented model helicopter rotor［C］.Proceedings of the 45th Annual Forum of the AmericanHelicopter Society.Boston，May，1989.

［19］ABHISHEK A，DATTA A，CHOPRA I.Prediction of UH－60Astructural loads using multibody analysis and swashplate dynamics［J］.Journal of Aircraft，2009，46（2）：474－490.