基于高效数值方法的一种高超声速飞行器外形气动力/热综合优化设计研究
王 荣,张学军,纪楚群,白 鹏,周伟江
(中国航天空气动力技术研究院,北京 100074)
WANG Rong,ZHANG Xuejun,JI Chuqun,BAI Peng,ZHOU Weijiang
(China Academy of Aerospace Aerodynamics,Beijing 100074,China)
0 引 言
飞行器气动布局外形设计需考虑诸多限制和约束因素,依靠设计经验通过纯手工方法调节参数优选方案的传统气动布局设计方式面临巨大的挑战,很难适应气动布局快速选型的设计需求。具有更高的设计效率和更强的设计能力的气动布局优化设计技术,为复杂气动外形设计问题提供了有效的解决途径。
当前,基于高精度数值模拟方法的气动布局优化设计技术,存在参数化建模、流场网格自动化划分以及气动性能鲁棒高效预测等技术障碍,制约了其在工程实际中的应用。而对于高速问题,由于基于定常Euler方程空间推进求解和流线追踪的气动力热预测方法计算效率高,鲁棒性好,在一定马赫数和攻角范围可满足型号气动力热特性快速评估要求,非常适合外形优化设计计算。因此,本文基于高效空间推进数值方法和流线追踪工程方法建立的气动力热特性快速预测技术,采用气动布局优化设计技术对一种参数化的高超声速飞行器完成了综合考虑气动力、热特性的外形设计研究。
外形气动力/热综合优化设计流程如图1,优化设计过程由优化模型模块驱动参数化外形造型、网格生成以及气动力、热计算模块形成封装的集成系统,根据设计条件自动实现寻优设计。

图1 外形气动力热综合优化流程Fig.1 Flow charts of the optimization progress
计算方法是气动布局优化设计的基础,本文首先简要介绍所涉及的计算和设计方法,然后对高超声速飞行器外形气动力/热优化设计研究过程进行介绍,最后给出设计结果与结论。
1 气动力/热性能高效预测方法
本文气动力/热特性快速预测方法基于空间推进求解无粘方程的高效数值方法和流线追踪工程方法,即,气动力预测采用基于高效空间推进的数值方法,气动热预测采用基于空间推进无粘数值解与轴对称比拟的气动加热积分关系式的流线追踪法。
1.1 无粘流场空间推进法
无粘流场计算通过空间推进法数值求解Euler方程完成。推进方向采用预测-校正两步法,侧面通量求解基于Godunov格式,根据Van Leer方法构造二阶精度,对梯度用Minmod限制器进行单调性限制。方法细节见文献[1-2]。
1.2 气动加热预测方法
气动加热预测方法采用流线追踪法[3-5]。通过以上空间推进数值方法获得无粘流场,然后利用无粘流场计算结果确定物面流线及尺度因子。沿流线运用Zoby[3]的方法积分得到物面气动加热率,在积分的每一步计算当地的边界层厚度,插值得到无粘流场在该位置处的流动参数作为边界层外缘参数。该气动加热快速预测方法的计算结果与相同条件下的地面试验数据对比表明,此方法可以比较准确地预测迎风区的气动加热率,二者的相对偏差不高于20%。
2 优化算法
传统经典的数值型优化算法计算效率较高,可靠性较好,也比较成熟,且对于解析的连续性问题的求解效果较好,但由于其构造策略的限制难以捕捉到全局最优解。与经典的以梯度为基础的优化算法相比,基于生物进化的自然遗传机制和金属晶体冷却退火的探索型现代算法不需要使用梯度,对函数性态的依赖较小,适应范围广,鲁棒性好,适用并行计算,在付出大量计算代价的情况下能够以很高的概率捕捉全局最优解[6-7]。因此为了结合两者的优势,弥补各自的不足,可将二者结合起来使用,这种兼顾效率和解的质量的取长补短方法在实践中是行之有效的。
本文采用探索型和数值型方法相结合的优化搜索策略,以模拟退火算法和序列二次规划法组合计算策略完成优化设计。
3 外形建模及网格划分
3.1 高超声速飞行器外形参数化建模
外形参数化建模是指选取描述几何形状的关键参数,以某种算法或几何绘图方法完成外形造型,并输出指定格式的表面模型的建模过程。
针对一种高超声速飞行器外形的几何特征,选取了数十个几何尺寸和几何位置参数来描述其物面形状,通过编写程序的方式完成外形参数化建模。图2给出了参数化建模后生成的初始外形和其中部分参数示意图。
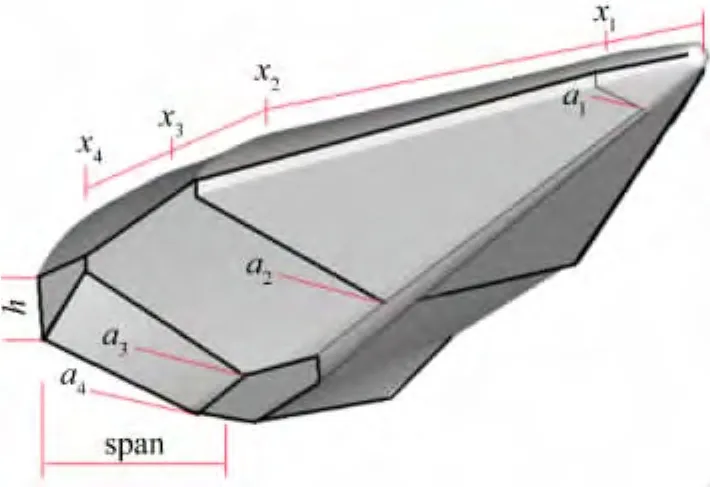
图2 初始参数化外形及部分关键参数示意图Fig.2 Original parameterized shape &design variables
3.2 流场网格划分
流场网格划分采用了单体结构网格生成技术。首先对每个轴向站位通过数值求解抛物化Laplace方程,从物面逐步推进到外流场边界生成二维网格面,然后连接从头部至底部各站位网格面最终建立三维空间网格。二维抛物化推进方法较成熟,容易控制网格的稀密及正交等特性,对一般外形均可得到质量较好的网格分布。图3为初始外形典型截面网格图。

图3 初始外形流场网格典型截面Fig.3 Illustration of slice grids
4 高超飞行器外形气动力/热优化设计
高超声速飞行器外形气动力/热综合优化设计研究,首先针对初始外形基本气动特性提出优化设计方案,然后进行优化计算,最后给出设计结果。
4.1 初始外形气动特性
图4给出了该飞行器初始气动布局高速飞行时(M=10)相对重心的俯仰力矩曲线,可以看出初始布局纵向气动特性是静不稳定的,这种布局对控制系统提出了较高的要求,需要通过静不稳控制完成飞行。因此,为了使该布局具有纵向静稳定大迎角配平的自飞行能力,需对初始布局进行设计,改变其纵向静稳定特性,同时也需兼顾气动热、装载空间和升阻性能等约束。对于该外形气动布局设计问题涉及较多的几何参数,并且有约束限制,通过数学优化的方法自动寻找期望的气动布局是可行的有效方法。
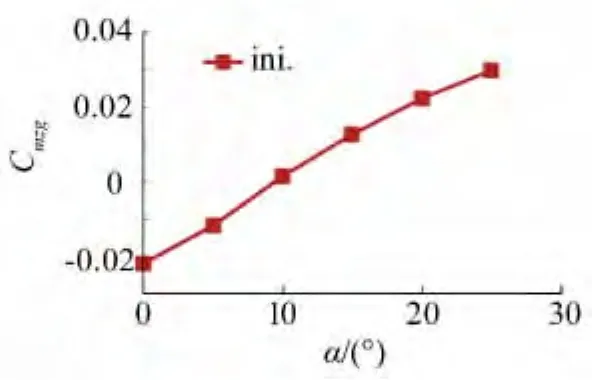
图4 初始外形俯仰力矩曲线Fig.4 Pitching moment curve of the initial shape
4.2 优化设计方案
本文选择巡航飞行状态作为优化设计点,巡航高度为H=40km,飞行马赫数为M=10。
为了实现纵向静稳定大迎角配平的气动设计目标,选定两个飞行迎角,一个为小迎角α=5°,另一个为大迎角α=20°,分别求出对质心的俯仰力矩Cmzgα5和Cmzgα20。将小迎角俯仰力矩Cmzgα5作为目标函数,使其最大化,将大迎角力矩Cmzgα20作为约束,限定其绝对量低于某一设定的阀值。随着优化进程推进,Cmzgα5增大,就能实现力矩对迎角斜率由正变负,达到所期望的设计目标。升阻性能是重要的气动指标,因此将α=20°的升阻比(L/D)α=20也作为优化的目标,使其最大化。从防热角度,表面最大热流qwm(非驻点)最小化是优化设计需要考虑的另一个设计目标。将以上气动力/热指标综合考虑,提出了如下多点多约束的优化设计方案,其数学描述形式可表示为:

其中,X是优化设计变量,由外形几何参变量组成的向量构成,Xu和Xd是X的上、下边界约束。
为了综合考虑各项目标,将多目标问题转化为单目标问题,即优化目标为最大化Cmzgα5、(L/D)α=20和qwm的线性加权求和值。a、b、c为比例因子,本文取a=100.0、b=1.0,c=0.01。
考虑载荷约束要求,α=20°升力系数CLα20不低于1,对于装载空间约束,限定第一横截面(图2中x1位置)内接圆半径r不低于130(图5)。对于等式约束在实际计算时采用松弛因子转化为不等式约束,松弛因子为一小的正数ε,如可取ε=0.002。
优化计算过程中参考面积取模型底面面积,参考长度为体长。

图5 截面装填约束Fig.5 Illustration of geometric constraints
4.3 优化设计
4.3.1 参数敏感性分析
为了比较全面地了解掌握几何外形参数对气动力、热特性的影响,通过实验设计方法研究了气动力、热特性对几何参数的敏感度。
实验设计包括实验取样、样本分析和方差分析三个步骤[8-10]。首先通过拉丁超立方采样方法在设计空间内生成由一系列不同外形构成的外形样本库;然后采用上文介绍的方法对每个外形样本逐个计算得到相应的气动力与气动热特性数据;最后根据气动力、热特性相对外形变量的计算结果拟合确定多项式系数建立多项式回归模型,相应的敏感性分析均基于该多项式模型。
多项式模型的拟合效果可通过参数R2或Radj2来表示[8]。表1给出了本文高速外形气动力、热特性经实验设计方差分析的结果,Radj2越接近1表示模型拟合效果越好,通常Radj2大于0.9都是可接受的,从分析结果看多项式模型对气动力、热特性基本上可以比较准确表示。
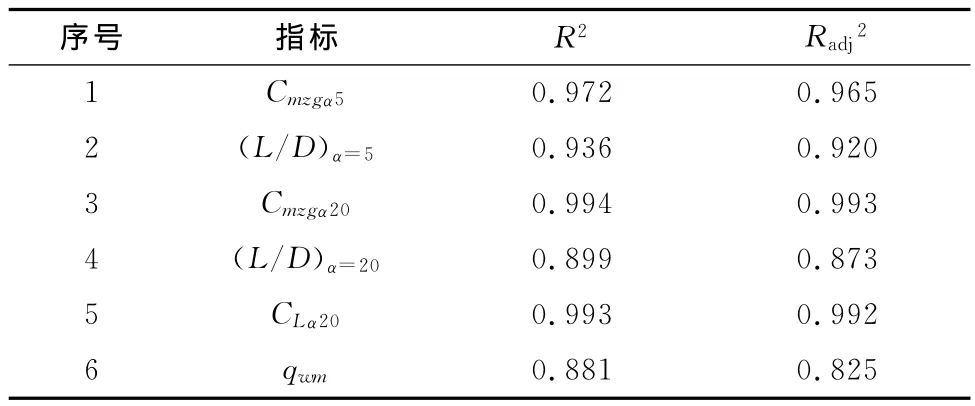
表1 实验设计分析结果Table1 DOE results
气动力、热特性对外形参数的敏感度可以用无量纲化的多项式模型的系数按百分数大小排序后以图形来表示。它反映了参变量改变引起的因变量平均变化量,也称作因子效应,是因变量对参数敏感性的度量指标。图6给出了高速外形气动力、热特性相对外形参数(图2)的敏感性排序图,图中给出了排序前二十的参数项。从图中直观地反映了哪些参数对气动力、热性能参数具有重要的影响作用,这对优化设计选择参变量作为优化设计变量具有参考指导意义。通过敏感性分析指出,俯仰力矩和升阻比对底面角度和截面轮廓尺寸较为敏感,而表面最大热流对前体几何参数比较敏感。
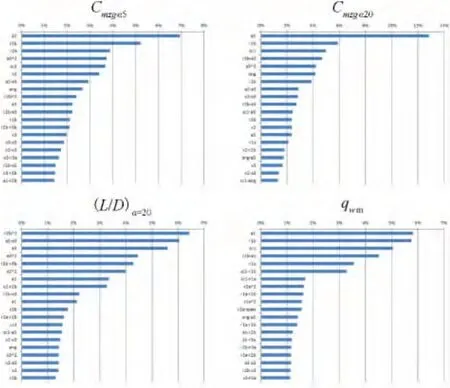
图6 参数敏感性排序图Fig.6 Rank of sensitive parameters on each factor
4.3.2 优化设计结果
根据以上参数敏感度分析情况,选取该高超声速外形剖面参数和平面参数共15个几何参数(部分参数示意见图2)作为优化设计变量,参数列表见表2,表中给出了设计变量的取值区间。这些几何变量是描述和确定该外形最主要的参数。

表2 优化变量设计空间表Table2 Searching space of design variables
对于以上优化设计问题,根据优化方案,运用模拟退火算法和序列二次规划法相组合的优化策略在表2给定的参变量设计空间进行搜索后,求得最优布局外形如图7(b)。相对初始外形(图7a),优化外形最显著的变化是抬头和翘尾,显然,该典型外形特征有助于增加小迎角俯仰力矩,有利于提高布局静稳定性。表3为最优布局外形设计变量的计算结果。

图7 优化前后布局外形Fig.7 Shape before and after optimization

表3 优化布局设计变量Table3 Optimum value of the design variables
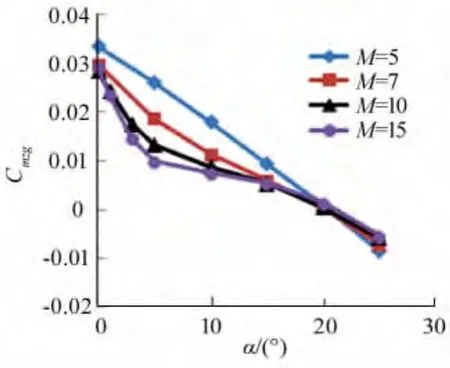
图8 优化外形俯仰力矩曲线Fig.8 The pitching moment curves of the optimum shape
图8给出了优化布局在不同马赫数下的俯仰力矩曲线,曲线清晰地表明优化布局气动纵向具有了静稳定特性,并在大迎角实现了配平,说明通过优化设计达到了所期望的设计目标。图9为初始布局与优化布局纵向压力中心曲线,优化布局压心随迎角增加逐渐后移至重心后面,变化规律性好,而初始布局在10°以上迎角时,压心位置在重心前面基本恒定,这反映了布局纵向稳定特性的差异。

图9 初始外形与优化外形纵向压力中心曲线Fig.9 initial and optimum shape pressure center curves
表4为气动布局外形经优化设计前后的计算结果。相对初始外形,在满足升力和截面空间约束的情况下,优化外形非头部驻点的最大表面热流降低24%,且小迎角力矩变号,但升阻比降低。图10为布局优化前后的升阻比曲线,优化布局升阻比有一定的损失。图11给出|Cmzgα20|≤ε时,通过大量计算得到的Cmzgα5与(L/D)α=20分布的前锋面,由此可见,静稳定性与升阻性能是冲突的,布局小迎角抬头力矩越大,大迎角巡航升阻比就越低,说明静稳定性增强是以牺牲升阻比为代价的。从另一面讲,放宽静稳定性要求有助于设计出升阻性能更好的外形。

表4 优化设计计算结果Table4 Calculation results of the shape before and after optimization

图10 初始外形与优化外形升阻性能曲线比较Fig.10 Lift-to-drag curves of the initial and optimum shape

图11 在20°迎角配平时Cmzgα5与(L/D)α=20前锋面分布Fig.11 Pareto front of Cmzgα5versus(L/D)α=20 under the trimmed attack angle
5 结 论
本文以优化设计方法结合高效气动力/热预测技术对一种高超声速飞行器气动布局外形完成了优化设计研究。对所提出的综合考虑气动力/热的多点多约束气动布局优化设计问题,在满足装载要求的前提下,通过优化设计实现了该布局纵向气动稳定特性改变和表面最大热流降低的设计目标。文中工作对此类外形设计有一定的参考指导意义。
[1]纪楚群,主编.导弹空气动力学[M].北京:宇航出版社,1996.
[2]JI C Q,LI J.Application of the Godunov method in the numerical simulation of complicated flow fields[J].ACTA Aerodynamica Sinica,2000,18(2):132-137.(in Chinese)纪楚群,李骏.Godunov方法在复杂流场数值模拟中的应用[J].空气动力学学报,2000,18(2):132-137.
[3]ZOBY E V.Approximate convective-heating equations for hypersonic flows[R].AIAA 79-1078R,1979.
[4]COOK J C.An axially symmetric analogue for general three-Dimensional boundary layers[R].R&M No.3200,British A.R.C.,1961.
[5]DeJARNETTE,FRED R.Aerodynamic heating on complex configurations[C].Technical papers conference on Advanced Technology for Future Space Systems,AIAA 79-0891,1979.
[6]唐焕文,秦学志.实用最优化方法[M].大连理工大学出版社,2005.
[7]DED K.Multi-objective optimization using evolutionary algorithms[M].Chichester,UK:Wiley,2001.
[8]MYERS R H,MONTGOMERY D C.Response surface methodology:process and product optimization using designed experiments[M].New York:John Wiley &Sons,1995.
[9]HONGMAN K.Statistical modeling of simulation errors and their reduction via response surface techniques[D].[PH.D Thesis].Blacksburg,Virginia,June 18,2001.
[10]GIUNTA A A.Aircraft multidisciplinary design optimization using design of experiments theory and response surface modeling methods[D].[PH.D Thesis].Virginia Polytechnic Institute and State University,Blacksburg,Virginia,1997.

