基于GPU并行处理的地形三维重建技术研究

杨秀峰，靳海亮，臧文乾

(1.河南理工大学，河南 焦作454000;2.中国科学院遥感与数字地球研究所，北京100101)

0 引言

随着计算机科学和计算机图形学的发展，三维地形的应用范围不断扩大，越来越多的涉及虚拟与现实、战场环境仿真、土地管理与利用、地理信息系统、娱乐与游戏等大规模的三维地形应用中，因此，如何快速的实现大规模的地形重建是一个值得研究的问题［1］。

近年来，很多学者对基于点云的三维重建技术进行了研究。目前基于点云的三维重建技术大致可划分为基于Delaunay三角剖分的方法、基于隐式曲面的方法和基于区域增长的方法［2］。在众多基于Delaunay三角剖分的方法中，Amenta［3］等人提出的基于中轴逆变换的Power Crust算法最具代表性。针对点云密度不均匀、带孔洞以及尖锐特征的任意点云，该方法都可重建出精密网格模型而不需要任何后期再处理，但是该算法需要进行复杂的三维Delaunay三角化处理，时间复杂度相当高，因此难以处理大规模地形的三维重建。基于隐式曲面的方法的核心是如何选取适当的隐曲面模型，其中比较著名的算法有Carr［4］等人提出的基于径向基函数的方法，Alexa［5］等人提出的基于移动最小二乘的方法和Kazhdan［6］等人提出的基于泊松方程的方法。这类方法能够较好的处理带有噪声的点云数据，但是容易丢失点云模型的原始数据信息和过渡平滑地物细节，并且针对大规模的点云，处理时间长。基于区域增长的方法一般都是从一个初始种子三角形出发，根据一定的判断原则添加点，不断向周边扩张直到所有数据点都被处理。其技术难点在于初始三角形的确定和新加入三角形点的判断。该方法可以实现大规模点云的三维重建，但是点云的重建质量过分依赖种子三角形的选取，并且在点云密度不均匀的情况下容易产生孔洞。Bemardin［7］提出的基于α-shape理论的滚球法(Ball Pivoting Algorithm，BPA)是比较著名的。目前，除了对上述单一方法的研究外，针对各种方法的融合使用也进行了大量的研究。王先泽［2］等人提出了一种基于Delaunay三角剖分和区域生长相结合的方法。首先对点云模型进行Delaunay三角剖分，然后从区域的边界边上添加新的三角面片，直到生成一张完整的三角网格模型。该方法在重建效率上有所提高，并能在一定程度上避免狭长三角形的产生从而提高生成网格的质量，但是针对大规模点云的重建，耗时仍是难以克服的问题。

整体而言，无论是单一的方法，还是多种方法的融合使用都无法有效的解决大规模点云三维重建的耗时问题。因此，本文提出一种基于GPU并行化的局部平面投影的地形三维重建方法，实现了三维地形的快速重建。

1 基于局部平面投影的地形三维重建算法

基于局部平面投影的方法是一种降维的三角剖分计算，在二维平面上实现三维重建。首先计算每个点的邻域信息，然后将每个点的邻域点投影到过该点的切平面上进行该点局部的Delaunay三角剖分，最后返回三维空间合并网格以及网格法向归一化调整。在本文基于点云的地形三维重建中主要包括k近邻计算、法向量计算、投影、径向排序和Delaunay近邻计算。

1.1 k近邻计算

k近邻计算一直是计算机图形学、机器学等领域的难点，特别当点云数据量大时，k近邻计算更是一个耗时的工作。因此，选择一个好的k近邻计算方法对于提高整个算法性能是至关重要。近似最近邻(approximate nearest neighbor，ANN)算法库是近年来运用比较广泛的一种k近邻计算方法，它是基于kd树搜索的一种方法，相对与传统的方法在性能上有75%提高，因此本文采用ANN算法库实现点k近邻。

1.2 法向量计算

法向量是点云具有的一个重要的局部特征，是进行点云处理必不可少的信息。本文中法向量的求解采用平面拟合的方法，主要用于邻域点的投影和排序，以及网格法向归一化调整。假设一点为p，其k近邻集合为Q={qi}，i=1，2，3，…，k，令=qi-p，应用最小二乘法，该点的法向量使得式(1)最小:

可得到3×3矩阵C:

容易证明，对于协方差矩阵C，其最小特征值对应的特征向量进行单位化可作为法向量的近似值。

1.3 投影

如图1所示，假设T为过某点的切平面，Q'= {q'i}，i=1，2，3，…，k为该点的领域点在其切平面上的投影点集合，则q'i可由在与所确定的平面内旋转得到

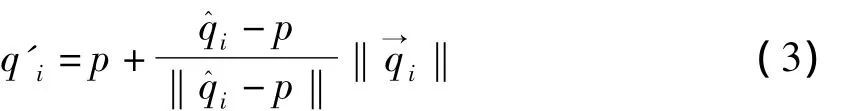
其中，q^i是qi在切平面上的正交投影

图1 旋转投影

1.4 径向排序

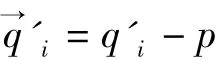
1.5 Delaunay近邻计算

对切平面上的投影点进行径向排序之后，利用二维平面三角剖分原理，从投影点集合中确定每个点的Delaunay邻近点，从而实现每个点的局部重建。如图2所示，l2是线段pq'i的垂直平分线，M是其中点，I是 pq'i-1的垂直平分线 l1与pq'i+1的垂直平分线l3的交点。如果I点不在p点与M点之间，则q'i是p点的有效Delaunay邻近点，然后继续下一点的Delaunay近邻判断;否则删除该点，并回溯判断〈q'i-2，q'i-1，q'i+1〉的有效性从而再次判断p'i-1是否为有效的Delaunay邻近点。直到没有点标记为无效的Delaunay邻近点，Delaunay邻近计算完毕。

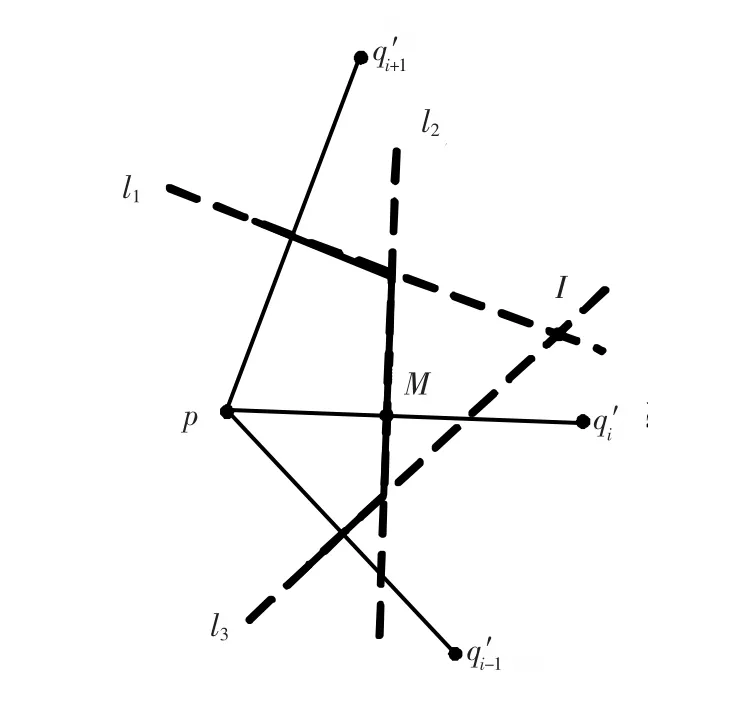
图2 Delaunay近邻点计算

2 基于GPU并行处理的地形三维生成

近年来，图形处理器(Graphic Processing U-nit，GPU)在通用计算构架方面的飞速发展，使其计算性能不断提高，计算能力已远远超过了通用处理器CPU，为加速三维重建提供了新的技术手段。2007年Nvidia公司正式发布的CUDA编程模型引发了GPU通用计算的革命，其将CPU作为主机，而GPU作为协处理器或者设备(device)。在模型中，CPU和GPU协同工作，其中CPU主要负责处理逻辑性强的事物和串行计算; GPU主要负责执行高度线程化的并行处理，实现大数据量的密集运算。

2.1 算法框架

通过对局部平面投影方法的分析，基于CUDA框架实现地形的三维重建中，邻域点的计算、网格合并和法向归一化在CPU完成，而针对每一个点的局部重构则在GPU中实现，其流程图如图3所示。

图3 基于CUDA的地形三维重建流程

首先，在CPU上读取点云数据，并调用ANN算法库进行k近邻计算。然后，将数据传入GPU中，接下来正式在GPU上进行局部平面投影算法。利用CPU控制内存分配和启动内核函数，而针对每一个点的局部平面投影算法的每个步骤都在GPU上执行，从而实现了并行处理。最后，在CPU上完成网格合并和法向归一化调整。

2.2 算法实现及结果分析

所采用实验设备为:Intel(R)Core(TM) i7CPU，主频1.6 GHz，Windows7操作系统，显卡为NVIDIA Quadro FX 880M。分别采用CPU模式下的局部平面投影方法和GPU模式下的局部平面投影方法对文家沟(图4所示)进行了三维地形重建，其结果如图5所示，并将2种重建方法的时间进行了比对，如表1所示。从统计的结果可以看出，利用基于GPU的局部平面投影算法重建地形的三维网格比基于CPU的方法有显著提高，特别在法向量计算和角度计算2个步骤中，分别有30多倍和40多倍速度的提升。

图4 文家沟三维点云模型

图5 文家沟三维重建网格模型

3 总结与展望

面对大规模地形三维重建耗时的问题，通过GPU并行处理的方式，使大规模网格生成的时间大幅降低。描述了局部平面投影算法的前提下，提出了一种基于GPU的局部平面投影算法，并基于CUDA框架实现了汶川文家沟三维地形的快速重建。实验结果表明，利用基于GPU的局部平面投影算法比传统的CPU模式下的局部投影算法有显著的提高，可见，在大规模地形三维重建中，GPU相对于CPU都有着相当大的优势。然而，由于实际点云数据的多样性和复杂性，总是会有点云稀疏或不均匀的情况，因此，重建过程或多或少都会导致洞的产生，孔洞修补成为必不可少的步骤。下一步工作，如何在GPU上实现孔洞的修补，从而快速、高质量的实现大规模地形的三维重建。

表1 运行时间结果对比

［1］ 徐 超.三维地形快速生成算法［D］邯郸:河北工程大学，2011.

［2］ 王先泽，李忠科，马亚奇，等.基于Delaunay三角剖分和区域生长的散乱点云重构［J］.四川工兵学报，2012，33(5):108-111.

［3］ Amenta N，Choi S，Kolluri R K.The power crust，unions of balls，and the medial axis transform［J］.Computing Geometry，2001，19(2):127-153.

［4］ Carr J C，Beatson R K，Cherrie J B，et al.Reconstruction and representation of 3D objects with radial basis functions［C］.Proceedings of the 28thannual Conference on Computer Graphics and Interactive Techniques，2001:67-76.

［5］ Alexa M，Behr J，Cohen-Or D，et al.Computing and rendering point set surfaces［J］.Visualization and Computer Graphics，IEEE Transactions on，2003，9 (1):3-15.

［6］ Kazhdan M，Bolitho M，Hoppe H.Poisson surface reconstruction［C］.Eurographics Symposium on Geometry Processing，2006.

［7］ Bernardini F，Mittleman J，Rushmeier H.The ball-Pivoting algorithm for surface reconstruction［J］.IEEE Transactions on Visualization and Computer Graphics，1999，5(4):349-359.