基于BP神经网络优化的灰色线性回归组合模型应用分析

杨世安，周世健，饶国华

(1.东华理工大学测绘工程学院，江西 南昌330013;2.江西省科学院，江西 南昌330096)

0 引言

灰色组合模型是将灰色系统模型(主要是GM(1，1))或灰信息处理技术融入传统模型后得到的有机组合体。GM模型具有弱化序列随机性，挖掘系统演化规律的独特功效，它对一般模型具有较强的融合力和渗透力。将GM模型融入一般模型建模的全过程，实现功能互补，能够使预测精度大大提高。然灰色线性回归组合模型可改善原线性回归模型中没有指数增长趋势和GM模型中没有线性因数的不足，故该组合模型更适用于既有线性趋势又有指数增长趋势的序列。

虽然灰色线性回归组合模型能较好的模拟观测序列，但为了使模拟更加精确，以进一步提高预测的精度。构建实测值与模拟值之间的比值序列G。目前，人工神经网络以强大的学习能力和高拟合精度广泛应用于各大领域，而绝大部分的神经网络模型是采用BP网络和它的变化形式，它是前向网络的核心部分，并体现了人工神经网络最精华的部分。故本文利用BP神经网络来优化组合模型预测精度。

1 灰色线性回归组合原理

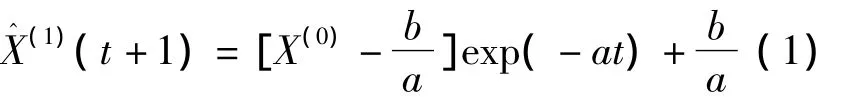
其形式可记为

用线性回归方程与指数方程之和拟合累加生成序列，即

其中参数v及C1，C2，C3待定。

为求以上参数，设参数序列

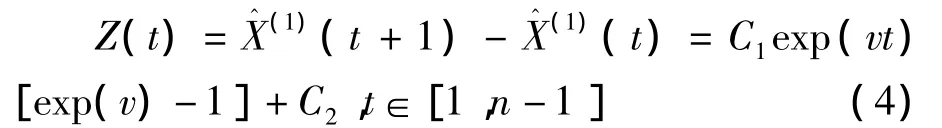
令Ym=Z(t+m)－Z(t)，则可得

由经典GM(1，1)模型［1］的原理可知

将式(4)中的X^(1)换成X(1)，由式(5)可得v的近似解，取不同的m可得不同的，以它们的平均值作为v的估值。经分析m=1，2，…，n－3，计算的的个数为(n－2)(n－3)/2，故得

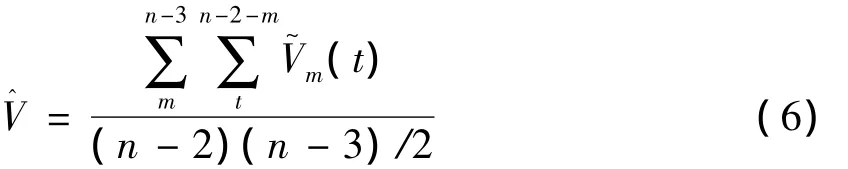
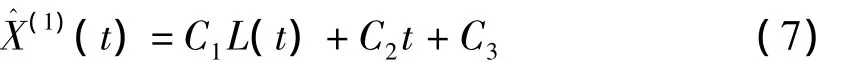
利用最小二乘法求得C1，C2，C3的估值，令

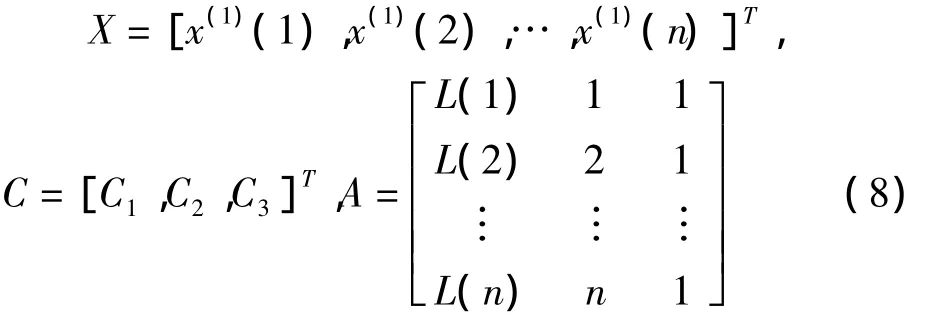
则有Y=AC，从而得

可得到生成序列的预测值为

则原始序列的预测值为

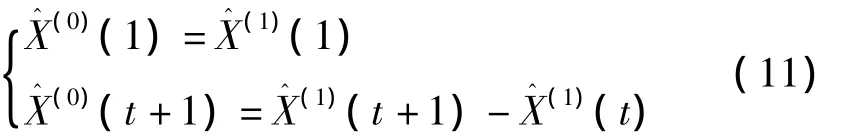
2 BP神经网络及优化过程

BP算法的基本思想［2，3］是，学习过程有信号的正向传播与误差的反向传播2个过程组成。正向传播是，输入样本从输入层传入，经各隐层逐层处理后，传向输出层。若输出层的实际输出与期望输出不符，则转入误差的反向传播阶段。误差反向是将输出误差以某种形式通过隐层向输入层逐层反传，并将误差分摊给各层的所有单元，从而获得各层单元的误差信号，此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程，是周而复始地进行的。权值不断调整的过程，也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可接受的程度，或进行到预先设定的学习次数为止。

优化思想:对于初始序列X(0)，进行灰色线性回归组合建模预测得到模拟值与预测值，针对不同的t时刻下的初始值与对应的模值有个比值关系G(t)，暂称之为吉比率即:

G(t)是一个新的时间序列，由于灰色线性回归组合模型的特性，该序列表现出值大多在1附近波形震荡变化。尝试利用MATALB中的人工神经网络工具箱对吉比率序列G(k)进行BP神经网络建模，得到新的吉比率G^，在设计BP网络时，使用5个隐含神经元，一个输出神经元，以前两期预测后一期做训练。则优化后的新预测值为

3 MATLAB实现步骤

经过以上论述，概括基于BP神经网络优化的灰色线性回归组合模型的MATLAB［4，5］实现的建模流程如下:

(1)1-AGO处理，将原始数据序列X0进行1次累加得X1;

(2)求解Z，由式(4)可得Z;

(5)构造X、A和C;

(6)依据最小二乘求解系数C1，C2，C3的估计值，参考式(9);

(7)由式(10)计算时间响应序列X2，将其紧邻差分可得X0的模拟值X3，其中，X3(1)=X1(1)参考式(11);

(8)由式(12)计算吉比率G序列;

(9)由BP神经网络对G序列进行训练和预测;

(10)由式(13)还原出X0的新模值X4;

(11)检验误差，计算残差，方差、相对误差和平均相对误差。

4 数学实例分析

选取的实验数据是，南昌市某段公路边坡的某测桩从2012年9月至2012年1月观测的10期沉降累计量，利用前8期建立灰色线性回归组合模型，预测后两期，并进行精度评定，时间相应序列为

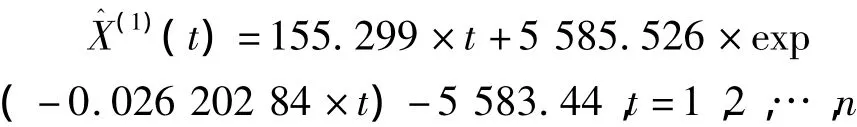
计算G(t)后，利用BP神经网络建模，并还原出新的预测值。将优化前后的模值列于表1中，并绘制数据对比线化图，如图1所示。

表1 灰色线性回归组合模型预测和基于BP神经网络优化后的数据/mm

图1 灰色线性回归组合模型优化前后数据对比线化图

利用灰色线性回归组合模型建模的拟合平均相对误差为4.69%，预测的第9、10期相对误差为4.6%、4.21%，而使用BP神经网络优化的拟合平均相对误差为0.31%，预测的第9、10期的相对误差为1.32%、1.76%。图1同样显出BP优化后的数据曲线更加吻合原数据曲线。

5 结束语

用MATLAB实现灰色线性回归组合模型算法，程序简洁、算法清楚。并利用其自带的神经网络工具箱进行BP神经网络优化，方便快捷。通过本文的数学实例证明:当实测值与预测值之间出现波动拟合时，它们的比值序列也同样具有波动性，此时采用BP神经网络对比值序列进行非线性拟合，具有非常高的预测精度;最后优化后的组合模型无论是拟合精度还是预测精度均比优化前的高出很多。这说明本文的优化模型用于改进灰色线性回归组合模型是可行有效的，同样也对变形监测数据的分析和预测具有参考价值。

［1］ 刘思峰，谢乃明.灰色系统理论及其应用［M］.北京:科学出版社，2008.

［2］ 田雨波.混合神经网络技术［M］.北京:科学出版社，2009.

［3］ 朱 凯，王正林.精通MATLAB神经网络［M］.北京:电子工业出版社，2010.

［4］ 唐丽芳，贾冬青，孟庆鹏.用MATLAB实现灰色预测GM(1，1)模型［J］.沧州师范专科学校学报，2008，24(2):35－37.

［5］ 胡晓东，董辰辉.MATLAB从入门到精通［M］.北京:人民邮电出版社，2010.