基于CORDIC的交流相位跟踪零差补偿方法及其实现*

伯　恩,段发阶,吕昌荣,张甫恺,冯　帆,梁春疆

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)

与传统的二维图像信息相比,物体的三维信息能够更全面、真实地反映客观物体,为人们提供更多的信息量。三维形貌测量技术是一种先进的精密测量技术,在质量检测、反向工程、身份认证、病理诊断、文物测量、文化影视等领域占有重要的地位[1]。基于正弦相位调制[2-3]的光纤干涉条纹投射测量技术是当前研究热点之一,在干涉条纹投射过程中,受环境因素影响,光纤干涉臂相位差不断变化,导致干涉条纹相位漂移,从而影响测量精度[4]。在光纤干涉条纹的相位稳定控制方法上,国内外学者进行了一定研究。Freschi等人提出光学高频相位调制和相位锁定以实现干涉仪工作在任意稳定工作点[5]。Moore等人利用压电陶瓷将干涉仪控制在正交稳定状态,利用PTAC技术实现条纹相位稳定[6]。程玉琪等人基于马赫-泽德干涉传感系统,对PTAC技术进行理论分析与实验研究,确定了PTAC相位检测的适宜工作状态[7]。恩德等人利用PTAC技术消除环境因素影响,对光学加速度计的相差信号进行提取[8]。王金海等人采用迈克尔逊干涉方法实现加速度信号光相位调制,综合PTAC技术和合成外差信号解调技术(SHSD)补偿误差并解调出加速度信号[9]。交流相位跟踪零差补偿技术是实现干涉条纹相位稳定的一种重要技术,其关键点是相位提取、补偿和求解。本文使用相位生成载波[10-11]技术提取温度变化引起的光纤干涉臂相位差,通过补偿实现条纹相位稳定;使用CORDIC算法快速求解光纤干涉臂相位差[12-14],发展了一种实时相位跟踪零差补偿方法。

图1　测量系统原理

1　系统设计

1.1　系统构成

测量系统原理如图1所示,He-Ne激光器作为输出光源,输出光束经过耦合透镜汇聚后,由光纤臂a进入2×2型光纤耦合器。经光纤耦合器分光后分别进入两光纤干涉臂b、c中,两光纤臂均紧密缠绕在圆柱形压电陶瓷上,光纤臂的输出端通过光纤夹固定,纤芯距足够小,构成马赫-泽德干涉仪结构。b、c光纤臂的输出端面等效为点光源,满足杨氏干涉条件。当满足远场近轴条件时,即纤芯距远小于光纤投射端到光屏距离时,可在光屏上投射高密度的余弦分布条纹。当物体表面存在高度差异时,干涉条纹会在空间范围内产生形变,CCD采集经过物体表面调制的变形条纹,结合系统结构参数,经后续图像处理即可实现被测物体表面形貌的重建。b、c光纤臂暴露在空气中,受温度、振动等环境因素影响,导致两光纤臂相位差发生改变,干涉条纹相位出现漂移。为了抑制环境因素影响,在光纤臂b、c的出射端面镀半反半透膜,利用出射端面的菲涅尔反射,在光纤臂d的出射端形成迈克尔逊干涉。光电探测器(PD)采集这一干涉信号,在相位补偿系统(PCS)中提取干涉臂相位差,将补偿信号闭环反馈给PZT驱动器。通过PZT的伸缩效应改变光纤臂c的长度,实现干涉条纹相位的稳定。

1.2　相位提取与补偿

对PZT2施加如下正弦相位调制信号:

M(t)=a·cos(ωt+θ)

(1)

其中,a为调制信号幅值,ω为调制角频率,θ为调制初相位。令PD检测的迈克尔逊干涉信号为S(t),按贝塞尔函数展开有:

S(t)=A+Bcos[zcos(ωt+θ)+α(t)]=A+Bcos[α(t)]×

(2)

其中,A为直流分量;B为交流分量幅值;z为相位调制度;相位α(t)包含光纤臂b、c间的固有相差和环境因素引起的相位漂移;Jn(z)是以z为变量的n阶第1类贝塞尔函数。

如图1所示,在相位补偿系统(PCS)中,采用相位生成载波方法提取相位α(t),其相位解调原理主要由载波生成、检波和相位解调构成。在载波生成过程中,将调制信号M(t)作为一倍频载波X1(t);对M(t)作平方运算,经低通滤波后作为二倍频载波G2(t):

(3)

在检波过程中,S(t)经中心频率为ω的带通滤波器BPF1得一次谐波分量H1(t);经中心频率为2ω的带通滤波器BPF2得二次谐波分量H2(t):

(4)

其中,*表示卷积运算,hBPF1(t)、hBPF2(t)为带通滤波器的响应函数。检波即是将载波与谐波分量相乘,经低通滤波器滤除载波信息,得到含有α(t)的两路检波信号V1(t)、V2(t):

(5)

其中,hLPF1(t)、hLPF2(t)为低通滤波器的响应函数。

α(t)=arctan[V1(t)/V2(t)]

(6)

在图1所示的相位补偿系统中,利用CORDIC算法求解相位α(t)。在相位-电压(P-V)转换模块中,由α(t)生成补偿信号VC(t),将α(t)补偿到零,kC为相位-电压转换系数。通过补偿的方式消除温度变化的影响,实现条纹相位稳定。

VC(t)=-kC·arctan[V1(t)/V2(t)]

(7)

2　CORDIC算法求解相位

2.1　算法基本原理

CORDIC算法的基本思想是:通过加减和移位操作,利用与运算基数相关的一系列特定角度不断偏摆来逼近预设的旋转角度。文献[12]给出了其基本形式,选择圆周旋转、矢量模式[13]时,利用反正切函数来求解相位α(t)。令迭代次数为i(0≤i≤n),(xi,yi)为矢量坐标,zi为未旋转角度,旋转角θi=arctan(2-i),di=sign(zi)为旋转方向控制因子,得到:

(8)

由式(6)可知,坐标点P(V2(t),V1(t))的相位角为α(t)。当CORDIC算法初始条件为(x0,y0,z0)=(V2(t),V1(t),0)时,以旋转角θi逐次逼近相位角α(t)的过程如图2所示。经过n次迭代有:

(9)

图2　CORDIC算法逐次逼近原理

2.2　算法结构选择

CORDIC算法的实现结构有递归结构和流水线结构[13-14]。递归结构消耗巨大堆栈空间,尤其是递归深度较大时。流水线结构可以减少计算周期,提高数据吞吐率。当数据稳定输出时,每一时钟均可以输出数据,增加流水线级数即可提高精度。CORDIC流水线结构如图3所示。

图3　CORDIC流水线结构

2.3　输入角度范围扩展

当输入角度为(-99.9°,+99.9°)时,CORDIC算法收敛[12]。S(t)相位变化为(-180°,+180°),所以必须扩展输入角度范围。根据坐标(V2(t),V1(t))判定P点所处象限,将各象限转换到第Ⅰ象限。经过若干级流水线计算获得相位zn后,将相位值还原到P点所处象限。象限映射如表1所示。

表1　象限映射表

2.4　常量序列存储

在流水线结构中,求解任意点P(V2(t),V1(t))的相位值都会使用增益因子{Kn}、旋转角{θn}等固定序列,预先将序列值存储在ROM区,可以提高相位α(t)的求解效率,保证信号VC(t)可以实时补偿到PZT驱动器中。

表2　Kn和θn常值表

2.5　相位求解误差

在CORDIC算法中,量化误差是影响相位求解的精度的主要因素[15]。在旋转迭代过程中,定义Q[·]为量化操作,‖P(i)‖=Ki,V(i)=[xi,yi]得:

Q[V(i)]=V(i)+e(i)

(10)

其中,e(i)=[ex(i),ey(i)],ex(i)、ey(i)表示xi、yi的量化误差。假设xi、yi数据位数为b,则有ex(i)≤2-b-1,ey(i)≤2-b-1。对e(i)取模得:

(11)

在CORDIC运算中,量化误差包含两部分:流水线中当前迭代的量化误差和之前所有迭代量化误差,定义F(n)为相位求解过程中的全部量化误差:

(12)

联立式(11)、式(12)可得

(13)

(V2(t),V1(t))为32bit,内部相位累加器初始输入为20bit,在CORDIC算法内部扩展为32bit。采用15级流水线结构时,相位误差曲线如图4所示,可见CORDIC算法的最大误差约为6.1×10-5rad。

图4　CORDIC相位误差曲线

2.6　算法仿真

图5　CORDIC算法仿真

3　实验与分析

如图1所示搭建测量系统,Uniphase公司He-Ne激光器产生632.8nm的稳定单模红光输出,功率为5mW。选择镜筒与透镜一体化的耦合透镜,在激光器与光纤臂a之间,激光器端的数值孔径AN=0.4,光纤端的数值孔径AN=0.16,放大倍数20X。F3284型2×2光纤耦合器工作波长633nm,数值孔径AN=0.13,与耦合透镜输出数值孔径相匹配。PZT2的正弦调制频率为2kHz,带通滤波器BPF1、BPF2的中心频率分别为2kHz、4kHz。两低通滤波器LPF1、

LPF2的截止频率均为200Hz。

3.1　kC标定

图6　kD标定图

3.2　条纹相位稳定

如图7(a)为某时刻PD检测信号S(t),受环境因素(主要是温度)影响,波形不稳定且局部波形受到很大干扰。提取相位α(t)经过PGC相位解调、CORDIC相位求解两个阶段,如图7(b)所示α(t)误差为2.75mrad。由于CORDIC求解相位的误差很小

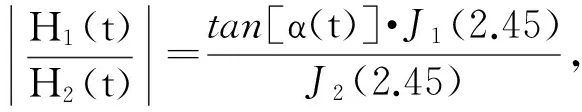
图7

4　结论

针对温度、振动等环境因素给三维形貌检测带来的不可忽略误差,本文使用正弦相位调制方法对干涉臂相位进行调制,利用马赫-泽德光纤干涉仪结构和杨氏双孔干涉原理实现干涉条纹投射,通过闭环相位补偿实现条纹相位稳定。在补偿的过程中,使用相位生成载波技术提取光纤干涉臂相位差,使用CORDIC快速求解相位差。该系统相位解调精度达2.75mrad,环境因素对干涉条纹相位的影响低于53.43mrad,较好地消除了环境因素对干涉条纹相位稳定的影响,通过实验论证了该测量系统的有效性。后续工作是将这一相位稳定技术应用于小尺寸物体表面的三维形貌高精度检测。

参考文献:

[1]孙宇臣,葛宝臻,张以谟.物体三维信息测量技术综述[J].光电子·激光,2004,15(2):248-254.

[2]Sasaki,Okazaki H.Sinusoidal Phase Modulating Interferometry for Surface Profile Measurement[J].Applied Optics,1986,25:3137-3140.

[3]Dubois A.Phase-Map Measurements by Interferometry with Sinusoidal Phase Modulation and Four Integrating Buckets[J].Opt Soc Am,2001,18(8):1972-1979.

[4]Zhang Fukai,Duan Fajie,Lv Changrong,et al.Fiber-Optic Project-Fringe Interferometry with Sinusoidal Phase Modulating System[J].Opt Eng,2013,52(6):065601.

[5]Freschi A A,Frejlich J.Adjustable Phase Control in Stabilized Interferometry[J].Optics Letters,1995,20(6):635-637.

[6]Moore A J,McBride R,Barton J S,et al.Closed-Loop Phase Stepping in a Calibrated Fiber-Optic Fringe Projector for Shape Measurement[J].Applied Optics,2002,41(16):3348-3354.

[7]程玉琪,董林军.干涉型光纤传感器PTAC法相位检测研究[J].传感技术学报,1992,5(1):22-27.

[8]恩德,陈才和,李岷,等.混合集成光学加速度计的信号处理和总体灵敏度[J].光子学报,2004,33(12):1428-1431.

[9]Zhang Chao,Duan Fajie.Closed-Loop Phase Stabilizing and Phase Stepping Methods for Fiber-Optic Projected-Fringe Digital Interferometry[J].Rev Sci Instrum,2011,82:113105.

[10]王泽锋,胡永明.干涉型光纤传感器相位漂移的无源解决方法[J].中国激光,2007,34(10):1417-1421.

[11]施清平,王利威,张敏,等.一种消除伴生调幅的光源调频型相位生成载波解调方法[J].光电子·激光,2011,22(2):180-184.

[12]Walther J S.A Unified Algorithm for Elementary Functions[C]//Proceedings of the May 18-20,1971,Spring Joint Computer Conference.ACM,1971:379-385.

[13]Meher P K,Valls J,Juang T B,et al.50 Years of CORDIC:Algorithms,Architectures,and Applications[J].Circuits and Systems I:Regular Papers,IEEE Transactions on,2009,56(9):1893-1907.

[14]姜建文,张朝杰,金小军,等.基于CORDIC算法的微小卫星发射机设计与实现[J].传感技术学报,2010(1):57-61.

[15]李桂英,陈磊,陈宇.高准确度多频调制激光测距算法研究[J].光子学报,2011,12:1888-1892.

伯恩(1989-),男,重庆忠县人,硕士研究生,主要从事激光测试技术与光纤传感技术方面的研究;

段发阶(1968-),男,湖南郴州人,博士,教授,主要从事测试计量技术及仪器,激光测试技术,计算机视觉检测技术和光纤传感技术等方面研究,fjduan@tju.edu.cn。