利用非线性规划方法最优化灰色预测模型

陈友军，何洪英，魏 勇

CHEN Youjun,HE Hongying,WEI Yong

西华师范大学 数学与信息学院，四川 南充 637009

College of Mathematics and Information,China West Normal University,Nanchong,Sichuan 637009,China

1 引言

邓聚龙教授20世纪70年代末、80年代初提出灰色系统理论[1]以来，该理论已广泛地应用于石油、地质、医学、工业控制、管理、农业等众多领域；作为该理论核心之一的灰色GM（1，1）预测模型，它建立在研究少数据、贫信息的不确定性问题基础上，已在各方面显示出它比很多其他预测方法更具优越性。传统的GM（1，1）模型参数辨识方法[1-2]和其他一些参数辨识新方法[3-9]，如灰色相对关联度方法、折扣最小一乘法、目标规划法、线性规划法等在建模的过程中都用ε(k)=x(0)(k)-(-az(1)(k)+b)作为实际值与模拟值的残差来建模。然而在评价模型优劣时都采用实际值与依据白化微分方程解的还原值x^(0)(k)的相对误差或者绝对误差平方和来判断的，所以建模方法与评价标准存在一定差异，即并不是所有的模型都满足只要残差平方和最小则其模拟精度最高，这就为进一步优化模型留下了空间。

从文献[1-2]可知，在检验一个GM（1，1）模型的模拟精度时，一般采用

计算得到模拟精度，其中 ε(avg)指 GM（1，1）模型的平均相对误差，且

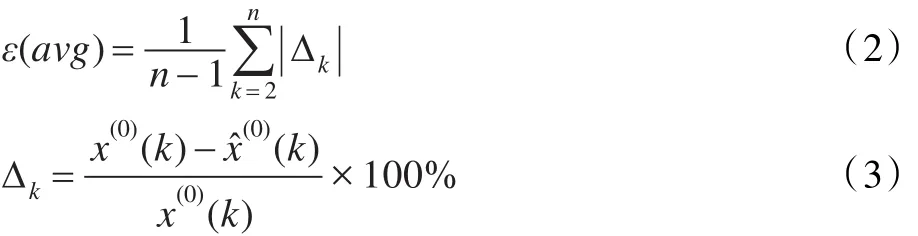
而模型的模拟值指通过GM（1，1）模型的时间响应序列[1-2]计算得到的还原值序列[1-2]，只是针对 GM（1，1）模型白化微分方程的初值选择方法不同，其时间响应式的计算方法也略有差异[3-9]。

很明显，要使GM（1，1）模型取得最大的模拟精度，则式（2）应当取得最小值，即GM（1，1）模型的平均相对误差应当取得最小值。本文就通过直接建立一个非线性规划模型，目标是使式（2）取得最小值，使用数学软件LINGO 11.0，可以直接求解得到这个模型的全局最优解[10]。通过大量的数据分析发现，采用这种方法建立的最优化GM（1，1）模型的模拟精度及预测精度都有了相当大的提高，并且新模型具有白指数重合律。

2 最优化GM（1，1）模型的建立

2.1 灰色GM（1，1）模型

定理1[1-2]设为非负原始数据序列，为X(0)的1-AGO序列，其中；灰色模型 x(0)(k)+az(1)(k)=b的背景值序列为Z(1)={z(1)(2),z(1)(3),…,z(1)(n)}，则

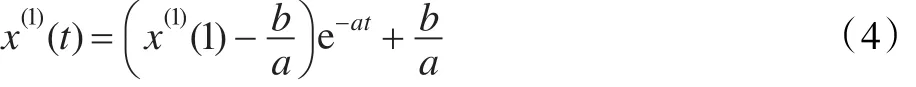
（2）GM（1，1）模型 x(0)(k)+az(1)(k)=b的时间响应序列为：

（3）还原值

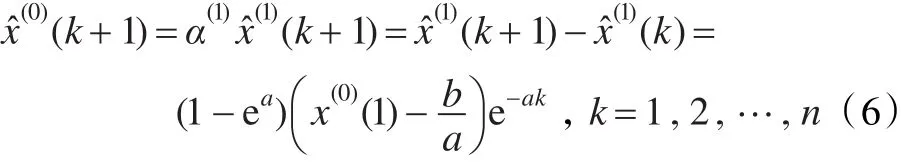
在上述GM（1，1）模型中，参数a为发展系数，b为灰作用量。

2.2 平均相对误差最小的非线性规划模型

针对GM（1，1）模型检验的一般方法，即一般使用最终模型的模拟值序列与原始数据序列间的平均相对误差的大小来评价GM（1，1）模型的好坏，最终模型的模拟值序列可以由上面的式（6）得到，故可以建立一个平均相对误差最小的非线性规划模型：

其中x(0)(k)为待建立GM（1，1）模型的原始值序列，x^(0)(k)为由式（6）得到的模拟值序列。上面模型中涉及到取绝对值及e-ak等形式，故它是一个非线性规划模型。

2.3 使用LINGO建立最优化模型

LINGO软件包是由美国Lindo系统公司（Lindo System Inc.）研制开发的，用于求解大型数学规划问题的软件包，它可以求解线性规划、整数规划、二次规划和非线性规划等问题，以及图论与网络中的组合优化问题[10]。对上面的模型（式（7）），本文就使用该软件来建模并求解，模型（式（7））转换成LINGO 11.0的模型如下：

上面模型求解结果中的A和B即为最优化GM（1，1）模型的发展系数和灰作用量。在对某一问题具体建模时，将原始数据序列放在上面模型最后的数据区，即“x0=”的后面，各数据间以空格分开，并在模型的最前面和中间指明数据个数，在LINGO 11.0中，可求得该模型的全局最优解。另外，上述模型中发展系数及灰作用量的变化范围，可根据实际情况设为一个较大的范围，而发展系数的变化范围一般应在内，最终的计算结果应在范围的中间而不应当取到范围的边界，否则，应当扩大相应的范围。

2.4 以x(1)(m)为初值的最优化模型

在文献[1-2]都提到了以x(1)(n)作为灰色模型微分方程的初值条件，其主要思想是基于灰色系统中充分利用新信息的原则；另外，文献[1-2]中也提到了选择最佳的x(1)(m)作为初值条件。在上面的非线性规划模型中再加上一个参数m，并且m的可取值为1到最大数据个数，改变后的模型如下：

模型中其他参数的意义与上面模型相同，但这样却可以得到在各种不同初值条件下的最优化模型，经大量数据分析发现，取任意初值得到的最优化GM（1，1）模型的模拟精度同样有了很大的提高。

3 数据模拟精度的比较

下面分别以文献[1]的原GM（1，1）模型、文献[6]中优化初始条件的模型、文献[9]的改进无偏模型与本文的最优化模型对白指数序列进行模拟。

（1）原始值序列

以白指数序列x(0)(k+1)=eAk为例进行模拟分析，取k=0，1，…，5，原始序列值如表1。

（2）以表1原始序列分别建立原模型，文献[6]模型，文献[9]模型和本文的最优模型，并得到它们的模型参数如表2。

表2中本文模型的数据是以x(0)(1)作为初值得到的。分析表2中的数据，当 A分别取0.1、0.5、1.0、3.0时最优化GM（1，1）模型的还原式分别为：

表1 原始值序列

因此，采用本文所述方法建立的最优化模型基本上是等于原始白指数序列的，所以无论是从模拟精度上还是从预测精度上来看，都是新模型优于其他模型。

从数值上看，新模型可能具有白指数重合律。事实上，根据前面的非线性规划最优化模型，有如下的定理。

定理2采用非线性规划模型参数建立的最优化GM（1，1）模型具有白指数重合律。

证明 根据式（7），当一个模型的实际值与模拟值相等时，最优化非线性规划模型取得最小值0，此时得到的解也是模型的最优解。对白指数序列：

由定理1，其模拟值序列为：

其中，a为GM（1，1）模型的发展系数，b为灰作用量。

由式（8）等于式（9）可得：

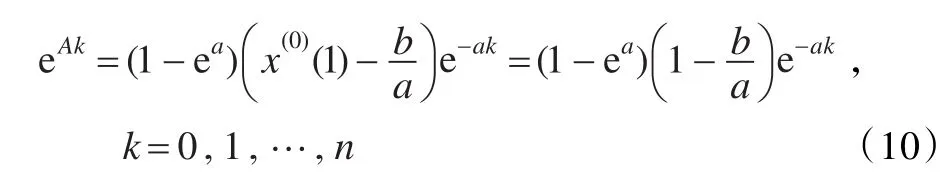
表2 各模型参数对比

综上，对白指数序列 x(0)(k+1)=eAk，当时，由式（7）建立的最优化非线性规划模型取得最小值0，其对应的最优化GM（1，1）模型的模拟值与实际值相等，所以采用新方法建立的最优化GM（1，1）模型具有白指数重合律。

4 实例分析

例1数据来源于文献[6]，其原始数据序列为（2.9836，4.4511，6.6402，9.9061，14.7781，22.0464，32.8893）。

利用文献[1]中邓聚龙先生的原始灰色建模方法，文献[6]的改进初始条件建模方法，以及本文的方法分别建立给定数据的GM（1，1）模型，得到的时间响应式分别为：

原始建模方法：

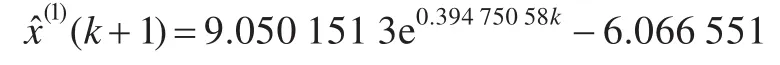
文献[6]建模方法：

本文方法：

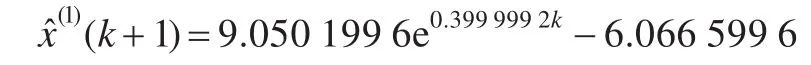
上面各模型具体计算结果如表3。

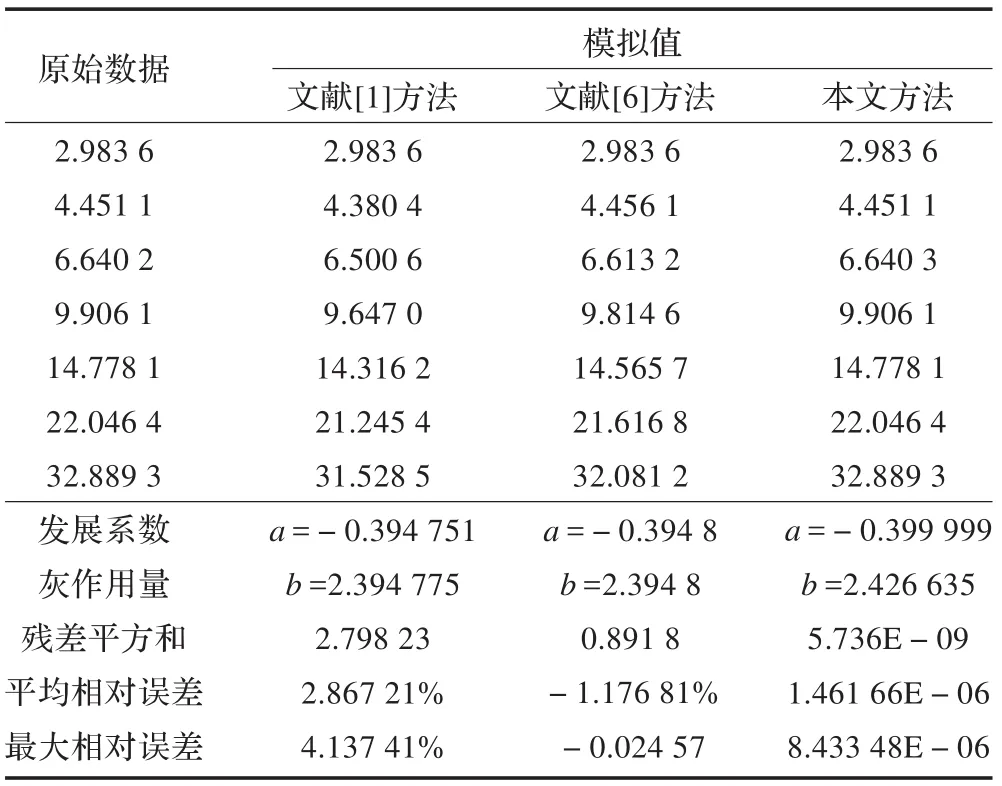
表3 各种建模方法计算结果对比

从表3可以得出以下几点结论：

（1）采用本文所述方法建立的最优化GM（1，1）模型的平均相对误差和最大相对误差比其他两种模型的都要低很多。

（2）对比表3的残差平方和发现，本文所述方法和文献[6]的建模方法的残差平方和都比原始模型小，这说明采用传统最小二乘法所得模型即使按误差平方和最小原则也不是最优。

平常中所说的模拟、预测精度高等价于“平均相对误差小”，笔者认为其合理的原因在于它将“实际值为0.1误差为0.2”与“实际值为100误差为0.2”严格区别开来，而“残差平方和最小”把它们视为同等误差。

综合分析上述两个例子可知，采用本文的新方法建立的GM（1，1）模型的平均相对误差是最小的，但是发展系数及残差平方和却各有千秋，这也充分说明，在建立GM（1，1）模型时，应当根据实际需要来选择一种最优的建模方法，而在评价一个GM（1，1）模型时，应当综合分析各种因素，并最终确定GM（1，1）模型的利用价值。当然，正如文献[1]所说，对于一个GM（1，1）模型，一般应当要求每个数据的相对误差小于20%，但最好是小于10%；要求模型的平均相对误差小于20%，但最好是小于10%。这也是评判一个GM（1，1）模型好坏的基本标准。

5 结束语

本文给出了一种利用建立非线性规划模型的方法来建立基于平均相对误差最小的最优化GM（1，1）模型的方法。对比其他很多的优化方法，该方法具有如下的一些优越性：

（1）采用这种方法建立最优化GM（1，1）模型对任何形式的数据序列都是有效的；不会像其他方法那样对某些数据序列有效，而对另一些数据优化效果却不明显，甚至起不到优化效果。

（2）由于LINGO是一套设计用来使构建和求解线性、非线性和整数优化模型更快、更容易和更有效的功能强大的工具，利用本文的建模方法建立的非线性规划模型，可直接利用LINGO 11.0求其全局最优解，操作简单，易于理解，而不必像其他方法那样经过麻烦的处理过程后才能得到相应的解。

（3）本文建立的最优化GM（1，1）模型是针对平均相对误差最小这个目标建立的，当然在建立非线性规划模型时还可以附加上其他的一些约束条件，如要求最大相对误差达到什么样的水平，或者残差平方和达到什么样的水平等，但是正如文章引言部分述的，一般人们所说的“残差”有两种，一种是另一种是前者一般应用于根据GM（1，1）模型估计发展系数a和灰作用量b，而后者主要应用于分析所建立的GM（1，1）模型的模拟精度及预测精度，事实上，按模型残差平方和最小的评价标准建立的最优模型也不是原始灰色模型，应是由后者导出的最优化模型，此处不再赘述。

[1]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].5版.北京：科学出版社，2010：146-197.

[2]党耀国，刘思峰，王正新，等.灰色预测与决策模型研究[M].北京：科学出版社，2009：101-180.

[3]Yang Shan，Wei Yong.Direct discrete grey model based on non-homogeneous exponential sequence[J].Journal of Grey System，2011，9（4）.

[4]曾波，刘思峰.近似非齐次指数序列的DGM（1，1）模型直接建模法[J].系统工程理论与实践，2011，2（31）：297-301.

[5]Xie Naiming，Liu Sifeng，Yang Yingjie，et al.On novel grey forecasting modelbased on non-homogeneousindex sequence[J].Applied Mathematical Modeling，2013，37（7）：5059-5068.

[6]Wang Y H，Dang Y G，Li Y Q，et al.An approach to increase prediction of GM（1，1）model based on optimization ofthe initialcondition[J].ExpertSystemswith Applications，2010，37：5640-5644.

[7]Li J J，Wei Y，Zhou R.The optimized background value of the GM（1，1） model which based on non-homogenous index series[J].Journal of Systems Science and Information，2010（9）：149-156.

[8]徐华峰，方志耕.优化白化方程的GM（1，1）模型[J].数学的实践与认识，2011，41（7）：163-167.

[9]Ji P R，Zhang J，Zou H B，et al.A modified unbiased GM（1，1）model[J].Grey Systems：Theory and Application，2011，1（3）：192-201.

[10]薛毅.数学建模基础[M].北京：北京工业大学出版社，2004：80-184.