高校毕业生就业率的影响因素分析
吕洪艳,杜 娟,刘志刚
(东北石油大学计算机与信息技术学院,黑龙江 大庆 163318)
0 引言
近年来,高校毕业生就业成为社会关注的主要问题之一,它影响到大学的声誉、教育事业的发展、社会对教育投资的信心,花费各级政府大量的人力、财力、物力。2013年,全国毕业生人数再创新高,接近700万,比2012年多了19万。大学毕业生增多了,就业岗位却不增反减。因此2013年被人称为“史上最难找工作一年”。政府和有关各方采取了许多措施提高高校毕业生就业率,并取得了一些成效。但由于各种原因,高校毕业生就业还面临着不少困难。本文的研究目的首先是想对影响就业率的因素进行结构分析,找出主要的影响因素,以期通过对主要因素改善,来提高就业水平,缓解目前大学就业恐慌的局面,为提高高校毕业生就业率提供一个有效的分析方法。
1 模型的建立
1.1 模型的设计
1.1.1 确定模型中所包含的变量
被解释变量——就业率;解释变量——大学排名、城市排名、师资水平(生师比率、博导数量)、学生素质(录取分数)、科研水平(管藏、重点学科数量)、学生人数。
1.1.2 变量说明及变量选取的依据
被解释变量:就业率,这里选为就业率排名,没有选择实际就业率值是由于各大学网站中,有很多大学没有将就业率公布出来,有的公布的只是几年来就业大概情况,而非确切的就业数据,有的公布出来就业率有很大的水分,所以这里用排名,相对于虚报的就业率,它更能反映各高校之间的差距。解释变量如下:
(1)大学排名。大学排名在一定程度上说明了各大学在人们心目中的地位,自然会影响各企业招聘的决策,这里选择的是具有一定权威的武书连的排名。
(2)城市排名[1]。大学的就业率与大学所在的城市有很大关系,经济发达、交通便利、信息通畅的中心城市会对就业率有积极影响。但是每个人心中对各城市的排名都有自己的看法,主观性很强,而国家统计局将GDP指数排名作为衡量城市经济水平的主要依据,所以,这里用各城市GDP的排名来表示城市的排名,虽然不够确切,但比较客观。
(3)师资水平是影响学生能力的重要因素。而学生能力是在企业招聘时最应该考虑的因素,因为企业招聘的目的就是找到合格的人才为企业服务。这里将生师比率、博导数量作为其二级指标[2]。
①生师比率。生师比率=学生人数/教师人数。这里的学生人数指本科生的数量,教师人数是专任教师的数量。选专任教师数量的原因是本科生教师的数量数据不可得,而专业教师在很大程度上反映了本科生教师的数量。
②博导数量。即博士研究生导师的数量,它代表了教师的水平,实际上这里选本科教师中在硕士学历/博士学历以上的教师的数量比较准确,但由于在各大学网站上并不能获得完整资料,只能获得一些学校的数据,而博导数量也是学校师资水平的很好的代表。
③管藏。指图书馆藏书数(不包括电子图书,单位是万册)。它在一定程度上代表了学生的知识面和学校的科研水平。
④重点学科数量。重点学科越多说明学生的工作越好找,它们之间是正相关的关系。
⑤录取分数。录取分数能够代表学生在大学的起点的水平,反映了学生的素质,与就业率有不可忽略的联系。
⑥学生人数。学生人数越多,找工作的人越多,表明就业压力越大。这里选用各大学的本科学生总人数,实际上它是各年的招生的结果,所以在一定程度上也可以代表各年招生的情况。
1.1.3 模型的选取
这里选用线性模型(指经变换后为线性模型):

实际上处理前应该是对数模型:

两端取对数后为:

根据所研究内容的特点和实际情况也选用了多元线性模型。这里假设χ1…χ8依次和上述8个解释变量对应,由于绝对数不利于研究比较,所以这里将绝对数变量取对数,为了保持其线性结构,实际上模型应该是(2),由于名次和生师比率在这里应该算相对数,最后,经变换后得到模型如公式(3),是适用于本研究的线性模型。
1.2 数据来源
以某一年为基准,以30所大学为例分析,通过高校网站、武书连主编的高考志愿填报指南、国家公布的城市GDP排名、教育部网站,得到以下数据,表示如表1。
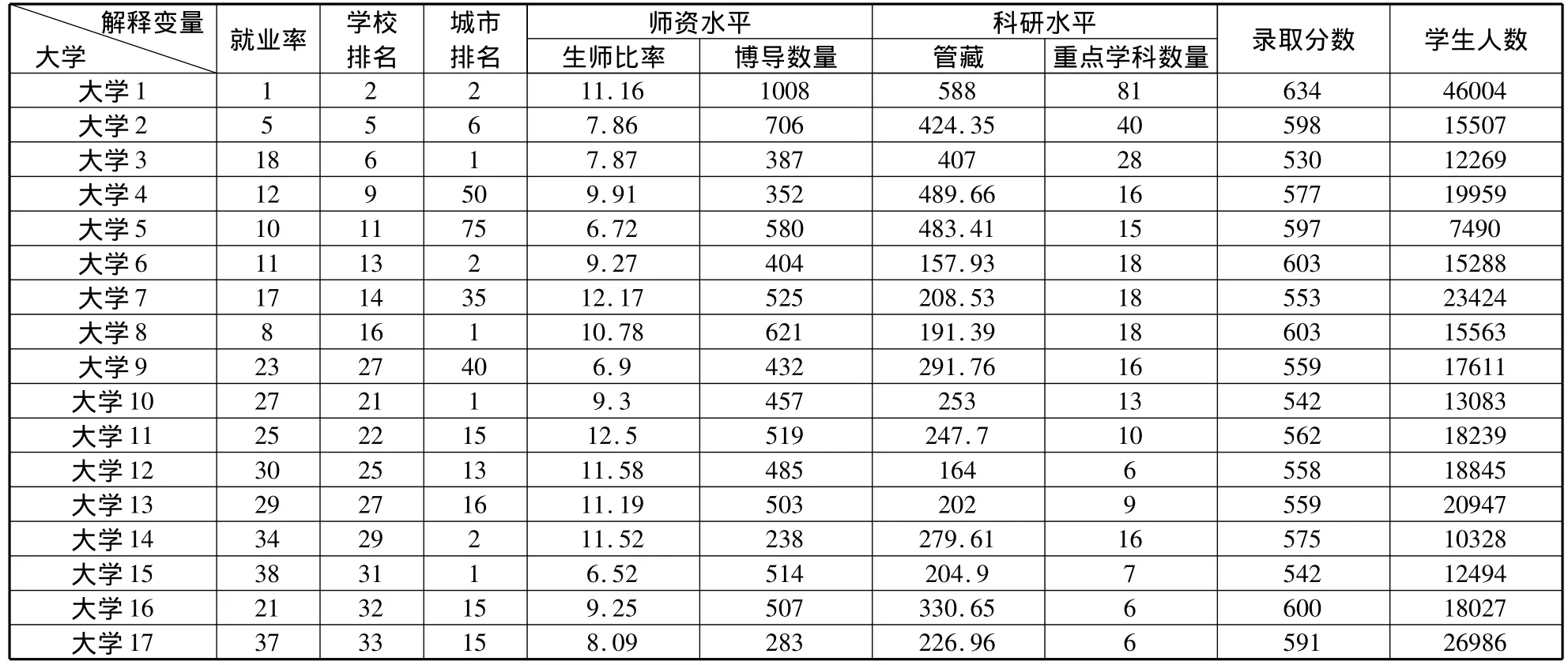
表1 大学各变量数据统计表

续表1
1.3 模型的估计
1.3.1 模型参数的估计
运用Eviews软件,对理论模型运用OLS进行参数估计,回归分析结果如下:
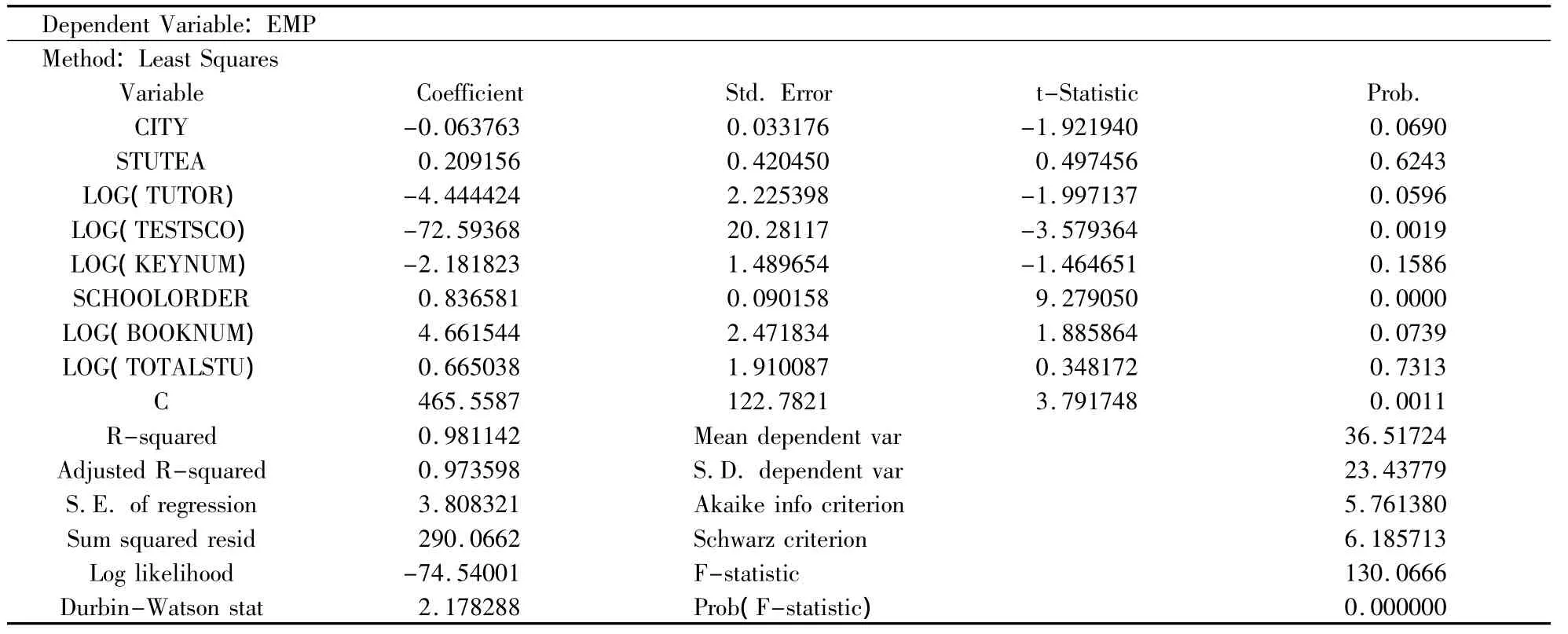
表2 Eviews输出结果
模型估计结果如下:

1.3.2 模型检验
1.经济意义检验。先从符号来看,从上面模型可以看出生师比、学校排名、馆藏、学生总人数和就业率排名成正比,说明它们的数值越大,排名越靠后,就是越不好,很显然,馆藏是通不过经济意义检验的。城市排名、博导数量、录取分数、重点学科数目与就业率排名成反比,可知,城市排名不符合经济意义检验。
2.统计检验。即主要是T检验、F检验、拟和优度检验。由上可知,拟合优度检验R2=0.973598,说明回归方程的解释能力为97.3%,即它们能对就业率排名的解释程度达97.3%,说明回归方程拟合优度较好。取显著性水平α=5%,单个回归系数的显著性检验-t检验:其中学生总人数对被解释变量的影响最不显著。所以先剔除学生总人数(因为数据取的是较好的大学,所以生师比相差不多,它的影响不显著是可以说得通的),重新进行OLS参数估计,得到回归结果显示重点学科数量影响不显著,将其剔除,重新进行参数估计,得到结果显示馆藏数量影响较小(随着经济的发展,现在几乎所有学校的馆藏量都够用,所以这里也可以将其剔除),将馆藏数量剔除重新估计后的结果显示博导数量作用不显著,将其剔除重新估计,显示城市排名作用不显示,实际上,大学所在的地理位置和就业率应该是主要因果关系,但这里结果显示没有主要关系,应该是数据搜集得不够准确导致的,这里也可以将其剔除,重新估计得到结果如表3。
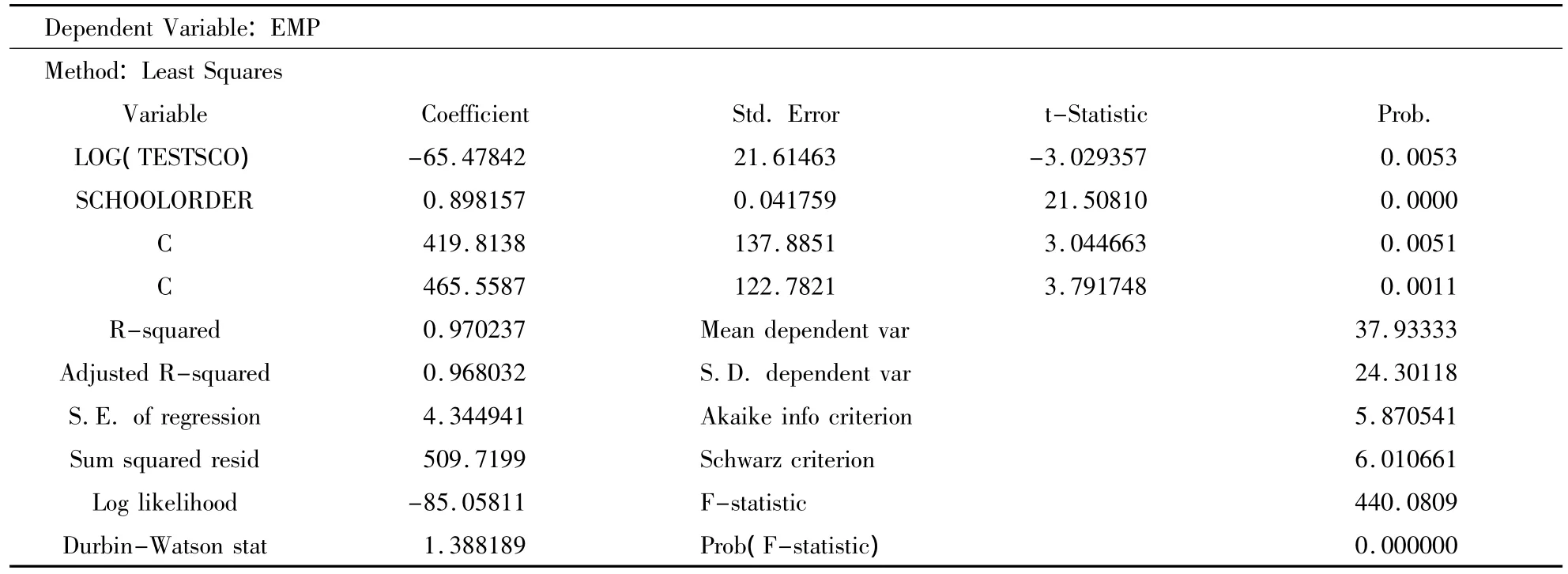
表3 剔除城市排名后Eviews输出结果
从上估计模型,得到如下结果:

单个回归系数的显著性检验-t检验:取α=5%,可以看出结束变量学校排名和录取分数通过显著性检验。
回归模型的总体显著性检验-F检验:α=5%,说明它们对就业率排名的共同影响是显著的,通过检验。
可以看到,所有变量都通过了显著性检验,拟合优度非常高,方程的显著性也非常好,而且从经济意义来说,学校排名与就业率排名成正相关,说明学校排名越往后,就业率排名越往后,这也符合事实。录取分数越高,就业率排名越往后,这也符合实际。所以以上回归结果通过了经济意义检验和统计检验。
3 计量经济学检验
(1)异方差检验。这里用怀特检验White Heteroskedasticity Test,过程与结果分析如下:
①无交叉项检验

表4 无交叉项检验Eviews输出结果简表
取显著性水平 α =0.05,Probability(nR2)=0.255245>0.05,说明模型不存在异方差。
②有交叉项检验

表5 有交叉项检验Eviews输出结果简表
同样,取显著性水平 α =0.05,Probability(nR2)=0.398048>0.05,说明不存在异方差。
(2)自相关检验:
①Durbin-Watson检验
由以上模型估计结果(表3)可知 Durbin-Watson stat=1.388189,一般来讲,经济领域内,DW低于1.5,则说明存在自相关。但这里计算可得(查表n=30,k=2):dl=1.28,du=1.57,Dl=1.28<1.388<du=1.57,说明不能确定自相关,运用②自相关检验的图示法通过定义残差项,运用Scatter diogram检验,得下图:
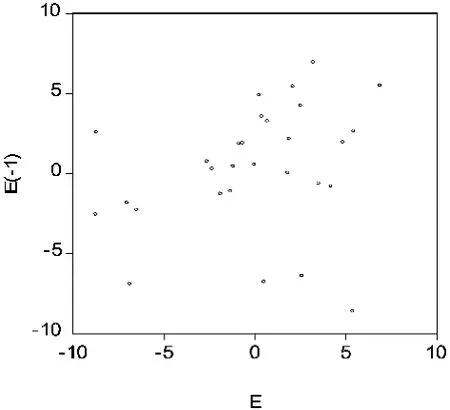
图1 Eviews输出结果
一般情况,横截面数据不存在自相关,但从图1可以看出,有一定的线性关系,说明存在自相关。
运用广义差分法处理自相关系数得到如下结果:

取α=5%,从以上结果可以看出通过了T检验、F检验。从调整后的结果来看,说明学校排名、录取分数对就业率排名的影响估计过小,从经济意义的角度看,学校排名对就业率的影响确实很大,这和客观现实也相符。而录取分数代表了学生素质、学生能力和就业率有着直接的联系。
(3)多重共线检验运用相关系数检验法,输出结果见表7。

表6 Eviews输出结果
从它们的相关系数来看,学校排名与入学分数之间的相关系数是-0.611,当|r|>0.8或0.9时,则可以认为这两个样本之间高度相关,样本间存在多重共线,这里说明它们之间存在负相关,但不是很显著,是可以接受的。
2 结果分析
从以上结果可以看出,学校排名、录取分数和就业率排之间存在着明显的线性关系,通过调整,估计的结果可以通过异方差、序列相关、多重共线的计量经济学检验,且经济意义方面也可以通过。这说明:①录取分数与就业率排名反方向变动,随着录取分数的增高,就业率排名靠后,即排名越好,这是和现实相符的。②学校排名和就业率同方向变动,随着学校排名的提升,就业率排名也提升,学校排名越不好,就业率越不好。比起录取分数,学校排名和就业的相关性更大,说明了企业在招聘时,也越来越重视大学的知名度。③在进行假设检验过程中,被解释变量城市排名、生师比率、管藏、博导的数量、学生人数和重点学科数量对就业率排名没有显著性影响,而大学排名与录取分数对其有明显的线性关系。④由于本文中的数据获取并不是很准确,只是取了较好的大学那部分,因此不具备普遍性,且由于是截面数据,也不能用于预测。
3 结语
虽然由于数据来源并不是很准备,且选择的高校没有普遍性,但本文为分析高校就业率影响因素提供了一个理论模型,通过模型分析,能得到客观的结论。在此基础上,根据结论采取针对性的对策,提高高校毕业生就业率能够有的放矢。但高校毕业就业的问题,不仅是教育界的问题,还是一个社会问题,涉及的问题较多,涉及面也较广,本文仅是提供一种分析方法,希望能引起届内人士对就业率的重视,促进对就业率研究的完善,而要从根本上提高高校毕业生的就业率,需要我们探索的路还很长。
[1]刘伟德.我国人口城市化水平对就业率影响和政策研究[D].杭州:浙江大学博士学位论文,2001.
[2]武书连.《挑大学选专业》高考志愿填报指南[M].北京:中国统计出版社,2012.

