铁电双层膜极化与介电极化率的尺寸效应
韩志友
(大庆师范学院物理与电气信息工程学院,黑龙江 大庆 163712)
0 引言
针对实验上观察到的铁电双层膜的剩余极化增大、介电常数与热释电常数增大、低损耗与高击穿电场、多回路电滞回线等[1-5]反常现象,理论上主要采取朗道唯象理论和横场伊辛模型理论来探究其物理机制。朗道唯象理论是宏观理论,其量子效应无法表现。而基于伊辛模型的微观赝自旋理论可以包含量子效应并且能够很好地描述铁电双层膜。目前,利用横场伊辛模型理论研究铁电双层膜的物理性质,都是假设构成铁电双层膜的两个铁电层表面与内部的性质相同,这是与实际不相符的。因为铁电层的表面到内部应该是连续结构[6-8]。
本文利用横场伊辛模型,考虑每一铁电层内都存在结构过渡层,并且在两个铁电层间界存在铁电耦合与反铁电耦合,设计了一个铁电双层膜模型来阐述其极化与介电极化率的尺寸效应。
1 模型与理论
图1为铁电双层膜理论模型。我们假设此铁电双层膜由两个不同铁电层A和B构成,且都具有结构过渡层。层A和层B分别由NA和NB层赝自旋组成,都平行于无限大的x-y平面,赝自旋都在格点位置上。极化方向沿z方向垂直于薄膜表面。假定双层膜的性质只沿z方向变化,在平行于薄膜表面的同一赝自旋层内的物理性质完全相同。
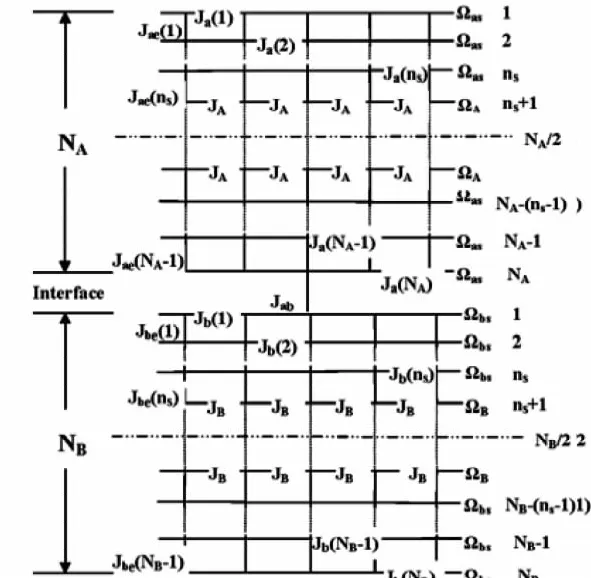
图1 铁电双层膜理论模型
二级相变铁电双层膜体系的哈密顿量可表示为:
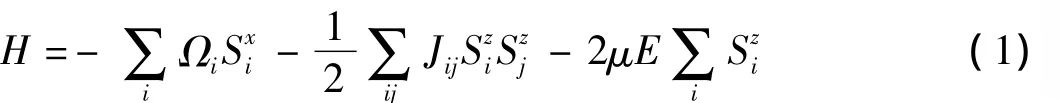
式中Ωi为隧穿频率,和分别表示i格点处自旋为1/2的x和z分量,Jij为格点i和j处赝自旋的相互作用,求和遍及所有最近邻赝自旋对。μ是第i个格点的偶极矩,E为外电场。
在此模型中,我们假设,如果格点i和j在层A(B)的同一个赝自旋层内,则Jij=Ja()m (Jij=Jb()m);如果两个格点在层A(B)的两个不同的赝自旋层内,则Jij=Jae()m (Jij=Jbe()m );但是当两个格点在层A(B)的内部,不在表面过渡层中,那么相互作用Jij的值就为体材料的值JA( JB)。如果两个赝自旋分别在层A和层B上,这时,Jij=Jab。同时,假设在每一层内的Ωi内部与表面不同。如果格点i在层A(B)的表面过渡层内,则Ωi=Ωas(Ωi=Ωbs);如果在层A(B)的内部,Ωi就为ΩA(ΩB)。
我们采用文献[9]中给出的函数形式来描述赝自旋相互作用与横向隧穿频率的不均匀分布,这些特殊的选取形式并不影响结论的一般性,具体函数关系的选择只会引起量上的差别,对定性的结论没有影响[10]。
应用平均场近似理论,第i层中沿z-轴方向的自旋平均值可以表示为:

其中

这里m取遍两个铁电层的所有赝自旋层。
方程(2)代表一系列方程,Rm可以通过迭代法求出。第m层的极化强度与Rm的平均值成正比,即:

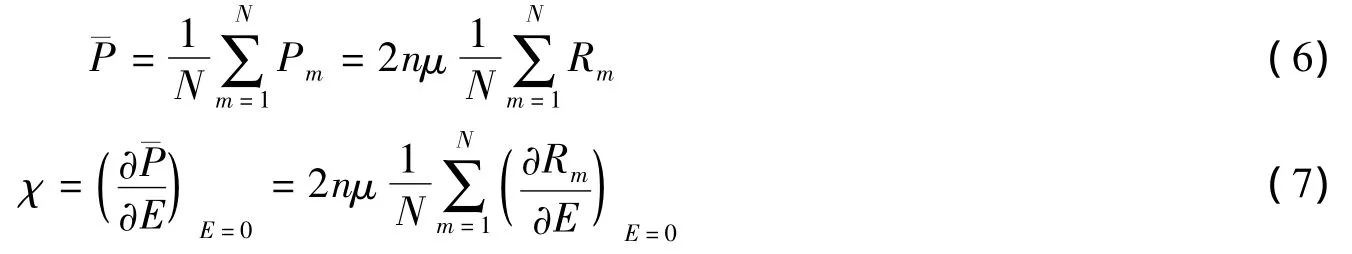
这里N表示双层膜的总厚度,即,N=NA+NB。
为简单并不失一般性,我们假设每一个铁电层的表面过渡层是对称的,并且两个铁电层内表面过渡层的赝自旋层数相同。规定总厚度N一定,JA/JB=0.5,ΩA/JB=0.5,ΩB/JB=1/3。设定t=T/TBC,这里TBC是层B的相变温度。
2 数值结果与讨论
图中参量ns表示层A和层B的一个表面过渡层包含的赝自旋层数。σ1(σ2)表示层A(或层B)表面附近的层内和层间相互作用与隧穿频率的变化强度。α1,α2,α3(β1,β2,β3)表示层A(或层B)表面过渡层的层内与层间相互作用和隧穿频率的强度。
图2分别给出了J>0时平均极化与介电极化率随温度的变化曲线。从图中可以看到平均极化随温度的变化曲线在层B较厚时(NA=2,NB=6与NA=4,NB=4),呈现三个缓台,分别为层A、层B及界面层处发生相变(温度从低到高)。其原因为:JA<JB,层A到达无序状态时,层B仍处在有序状态,由于铁电耦合的存在将影响层A。在层A较厚时NA=6,NB=2呈现两个缓台,分别为层A、层B的相变。此时层B与界面层的相变合并。与此对应,介电极化率分别呈现三个峰值,对应于层A、层B及界面层处发生相变(温度从低到高)和两个峰值分别为层A、层B的相变。该结论与文献[11]报道的相一致。

图2 J>0时平均极化与介电极化率随温度的变化
图3描述了J<0时,平均极化与介电极化率随温度的变化曲线。平均极化先随温度的升高而增大,然后随着温度的升高而减小,尤其是层A较厚时更加显著。这是由于层A的相互作用较弱,反铁电耦合对平均极化的作用占主导。当层A完全无序,这是平均极化曲线呈现最大值,而后只有层B有序。介电极化率随温度的变化曲线与J>0的情况相似,不同的是双层膜完全相变时的峰宽变窄。这些现象与实验上观测到的现象完全符合[12]。
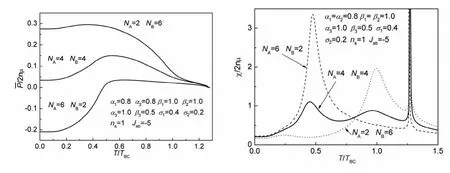
图3 J<0时平均极化与介电极化率随温度的变化
3 结语
(1)在双层膜总厚度一定下,J>0时,当层B较厚,平均极化与介电极化率随温度的变化曲线分别呈现三个缓台,三个峰值。
(2)J<0时,层A较厚时,平均极化先随温度的升高而增大,然后随着温度的升高而减小。介电极化率随温度的变化曲线在层A较厚时出现两个峰,层B较厚时呈现三个峰值。
[1]Tsurumi T,Harigai T,Tanaka D,et al.Artificial ferroelectricity in perovskite superlattices[J].Appl.Phys.Lett.,2004,85(21):5016-5019.
[2]Salev P,Azad M M,Grigoriev A.Electrical measurements of dielectric nonlinearities in ferroelectric bilayer thin films[J].J.Appl.Phys.,2013,113(7):074104.
[3]Mohammed M S,Auner G W,Naik R,et al.Temperature dependence of conventional and effective pyroelectric coefficients for compositionally graded BaxSr1xTiO3films[J].J.Appl.Phys.,1998,84(6):3322 .
[4]Ranjith R,Nikhil R,Krupanidhi S B.Interfacial coupling and its size dependence in PbTiO3 and PbMg1/3Nb2/3O3multilayers[J].Phys.Rev.B.,2006,74:184104-1-184104-10.
[5]Wu J G,Zhu J L,Xiao D Q,et al.Double hysteresis loop in(Pb0.90La0.10)Ti0.975O3/Pb(Zr0.20Ti0.80)O3bilayer thin films[J].Appl.Phys.Lett.,2007,91:212905.
[6]Cui L,Lü T Q,Xu X,Zhou J.Theoretical study on the mechanism of abnormal dielectric susceptibility behaviors of ferroelectric bilayer films[J].J.Appl.Phys,2009,105(10):104104-1-104104-7.
[7]Lü T Q,Cao W.Generalized continuum theory for ferroelectric thin films[J].Phys.Rev.B,2002,66(2):024102.
[8]Sun P N,Lü T Q,Chen H,et al.Influence of Surface Transition Layers on Phase Transformation and Pyroelectric Properties of Ferroelectric Thin Film[J].Chin.Phys.Lett.,2008,25:3422-3425.
[9]Cui L,Han Z Y,Li Y C,et al.Dielectric susceptibility of a ferroelectric bilayer film with surface transition layers[J].Superlattice and Microstructures,2012,51(2):462-470.
[10]Cui L,Xu Q,Xu X,et al.Pyroelectric properties of a ferroelectric superlattice with surface transition layers[J].Journal of mater sciences,2012,47(9):1780-1786.
[11]Cao H X,Li Z Y.Thermodynamic properties of temperature graded ferroelectric film[J].J.Appl:Condens.Matter,2003,15:6301.
[12]Qu B D,Evstigneev M,Johnson D J,et al.Dielectric properties of multilayered thin films prepared by pulsed laser deposition[J].Appl.Phys.Lett,1998,72(11):1394.

