基于长基线系统绝对测阵的测距修正算法优化

张宏伟，林 芳

(大庆师范学院物理与电气信息工程学院，黑龙江 大庆 163712)

0 引言

绝对测阵是整个长基线水下定位导航测量中不可或缺的环节，其精度直接影响导航定位精度［1－3］。系统测阵时采用的是“询问－应答－接收”方式测距，根据空间交汇原理对应答器进行定位，由于母船有速度，导致发射和接收点分离，所测得的测距数据与实际距离存在偏差，从而影响定位的精度。本文通过对测距修正算法进行近似优化提出新的算法公式，基于测阵模型的仿真比较表明，该方法可行，海试证明能有效降低修正误差。

1 测量距离修正原理

长基线水下定位导航系统绝对测阵利用“水声应答测距、空间球面交汇定位”原理进行工作［4－5］，系统在静止情况下定位。由于在绝对测阵过程中，测阵母船是运动着的，而系统又是采用询问—应答方式测距，假定母船作匀速直线运动，由于系统采用“询问—应答”方式测距，故发射和接收不在同一点上，这样水声收发机所得到的测距数据实际上是两个不在同一直线的距离之和，如图1所示，即母船到应答器1的实测距离为，而不是R11;同样母船到应答器2的实测距离为，而不是R21，所以有误差。产生这种误差的原因是母船速度，速度越大则误差也越大，同时，各应答器检测并确认询问信号到发射应答声脉冲还有一定的时延，一般为10～20毫秒左右;水声收发机检测并确认应答信号的电路时延一般也有4～8毫秒。这些时延都将使得各测距值比母船到各应答器的实际距离要大，因此，必须对其进行修正，使各测距值统一归算到发射时刻母船到各应答器的距离。

推算出距离及时延引起的测距误差的修正公式如下:

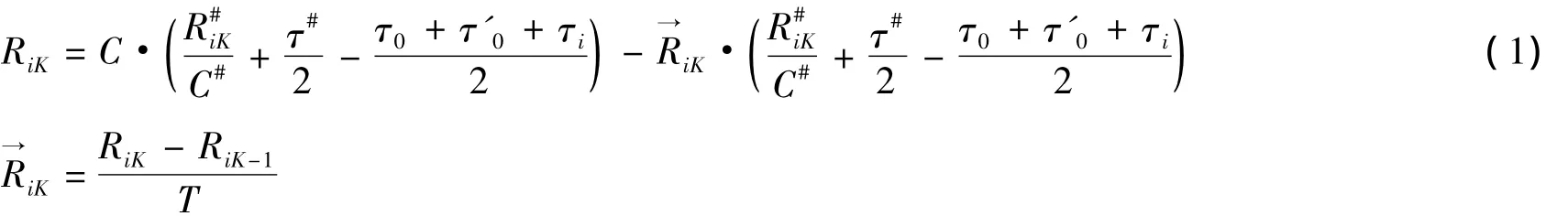
式中:

RiK——第K帧发射时刻母船到应答器i的距离;

C——平均声速;

RiK－1——第K－1帧发射时刻母船到应答器i的距离;

C#——水声收发机的预置声速(通常为折算后的平均声速);

τ#——水声收发机的预置时延(通常设为0);

τ0——声头和水声收发机的接收时延(可通过试验前计量得知);

τ'0——声头和水声收发机的发射时延(可通过试验前计量得知);

τi——应答器i的时延(可通过试验前计量得知)。

图1 测量斜距修正示意图

其中

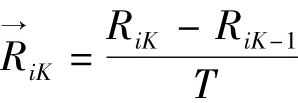
式中的 RiK和RiK－1用和(第K－1帧水声收发机通道i的测距读数)近似代替，将测距均值近似做为发射声脉冲时刻母船到应答器的距离，得到

2 测距修正公式

以一个目标应答器为例，对测距过程进行分析，测距分析图如图2和图3所示。其中O为目标应答器，a1、a2分别为第一帧询问声信号发射点与接收点，b1、b2分别为第二帧询问声信号发射点与接收点，T为声信号发射周期，t1、t2分别为第一帧和第二帧水声收发机所测的声传播时延(双程)，R11、R12、R21、R22分别为第一帧和第二帧声信号往返所传播的实际距离。

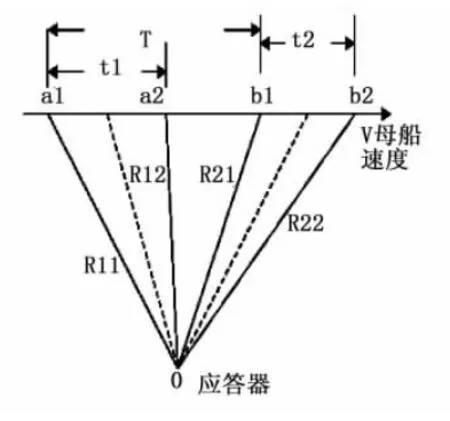
图2 T＞t1情况测距分析图

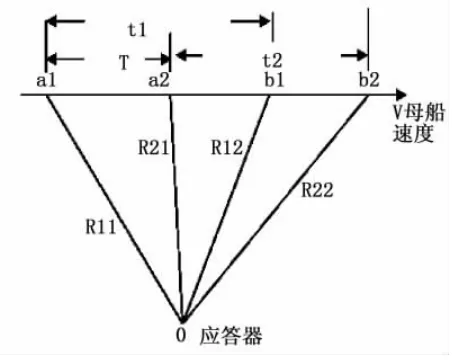
图3 T＜t1情况测距分析图

根据测距修正原理及测距分析图，可以得到:

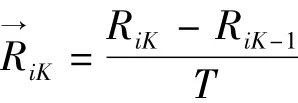
应用在图2中，可以等效于

而通过水声收发机测距所反映出来的数据只是R#1和R#2，并不能得到真实的R21和R11。根据图2中的时间关系，可以得到以下结论;

a1、a2间的时间为 t1，b1、b2间的时间为t2，a1、b1间的时间为 T，则有 a2、b2 间的时间为 T－t1+t2，这样用(3)式可以得出如下等式;

整理后得到

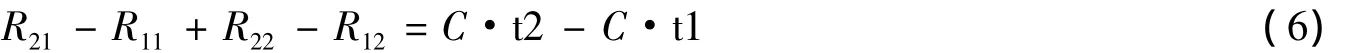
如果将给上式两边同除以一个T，并将4式代入即:

由于a2、b2两个接收点间隔时间为T－t1+t2，同时两测量点临近，母船以匀速直线方式运动，可以把这个过程中母船对应答器的径向速度看做常量，记作，则有:

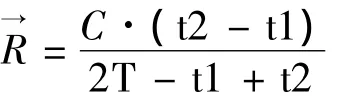
(8)式通用的描述可以表示为

同理图3推导出来的公式与(9)式形式相同，考虑到模糊周期的因素，这里不做描述。

通过分析可知，仅根据水声收发机测得的距离来解算径向速度，把平均距离作为发射时刻母船到应答器的距离，将会造成较大误差，而优化后算法能更近似相邻两测量点的径向速度。

3 仿真分析

3.1 利用模拟对称点的方法

我们模拟对称点测量的测阵方法，如图4所示，针对一个目标应答器S在其的四个相对对称的方向上选取4个测量区域，每个区域测量8次，每次间隔15m，在测量区域内母船保持5节的低速直线航行。

图4 对称点测阵分析图

通过仿真我们得出公式(2)和公式(6)产生的测距修正误差，如表1所示。这里选取平均声速1500m/s，测距仪脉冲周期6秒，母船航速5节(2.5m/s)对目标阵元S(3100，1700)进行测试。

表1 测距偏差

表1反映出测距修正误差在解算中是不可避免的，通过优化近似新的测距修正公式造成的误差较原来有较大幅度的降低，可见优化近似后的公式对距离修正作用较明显。

下面我们综合由声速测量误差、GPS定位误差、测时误差和测距修正误差共同作用的情况，比较公式(2)和(6)对绝对测阵精度的影响。选取水声收发机和应答器时延值为4ms和10ms，平均声速1500m/s，测时误差(－1ms，1ms)，分别在声速误差(－2m/s，2m/s)、(－3m/s，3m/s)和 GPS 定位误差(－3m，3m)、(－5 m，5 m)情况下做对比。

表2 误差分析

从表2可看出在相同的随机误差作用下，公式(6)相比公式(2)能较为有效地提高绝对测阵的精度。由此可以证明，新测距修正公式能有效地降低近似解算造成的误差。

3.2 海试验证

图(5)是在南海某海域试验中使用半矩阵型航路测阵后给运动目标导航的轨迹，其中1#、2#、3#、4#、5#和6#潜标构成了一个2km*2km+2km*1km小跟踪阵，利用半矩形阵航路对海底应答器进行测阵。测阵完毕，利用测阵结果对目标船进行导航。良好海况，目标船以小于5节航速在阵中低速航行。

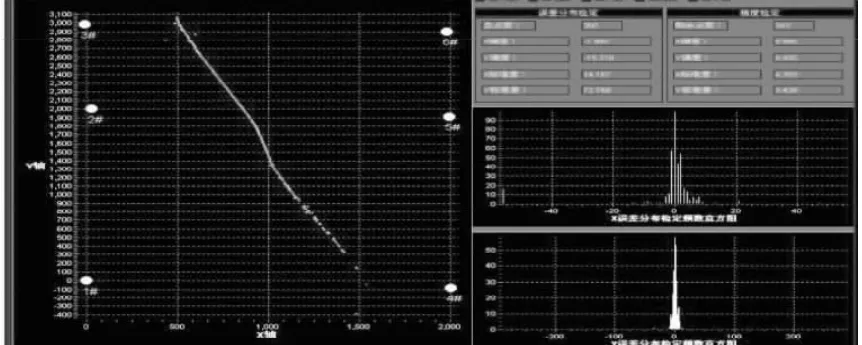
图5 海试结果图

测阵时，航路航行时间大约为1.2个小时。同时测得系统对运动目标导航精度满足水声定位系统的精度要求，从导航软件可以看出，运动目标轨迹与GPS的轨迹几乎重合，完全符合水声定位系统的精度要求，证实了半矩形阵测阵使用成功。为大范围导航定位打下了坚实的基础。

4 结语

通过对绝对测阵时，由于算法不同导致误差相差很大，在相同的因素影响下，改进的测距修正公式在理论上能够有效地减小误差，对长基线系统的测阵和导航的定位解算精度有一定程度的改进，具有良好的工程推广应用价值。对其他水声定位系统的测距修正具有借鉴意义。

［1］李启虎.水声学研究进展［J］.声学学报，2001，26(4):295－301.

［2］李守军，包根生，吴水根.水声定位技术的发展现状与展望［J］.海洋技术，2005，24(1):131－135.

［3］Kussat N.H.，Chadwell C.D.，Zimmerman R.Absolute positioning of an autonomous underwater vehicle using GPS and acoustic measurements［J］.IEEE Journal of Oceanic Engineering，2005，30(1):153－164.

［4］杨道军，许伟杰，翁国忠.船底运动小直径圆柱受力挠曲分析［J］.海洋工程，2006，24(4):49－55.

［5］陈子，许枫.GPS时钟同步在水下定位系统中的应用［J］.微计算机应用，2008，29(8):86－89.