网络控制系统多参最优性能研究
(武汉科技大学信息科学与工程学院,湖北 武汉 430081)
0 引言
网络控制系统(network control system,NCS)是目前研究的热点问题,研究的热点之一在于考虑网络时延、数据丢包、量化误差等对系统性能的影响。文献[1]~[2]分别研究了数据丢包和乱序NCS稳定性问题,建立了Markov模型,设计了状态反馈控制器;文献[3]采用一种新的随机计算方法,针对时变时延,研究了丢包、通信约束下NCS的稳定性;文献[4]针对前向通道具有网络时延,研究了系统的最优性能跟踪问题。
本文在文献[4]的基础上考虑了反馈通道具有数据丢包的情形,不仅分析了跟踪性能与非最小相位(non-minimum phase,NMP)零点、不稳定极点、时延和数据丢包等单个参数的关系,而且还研究了这些参数相互耦合时六种情形下对跟踪性能的影响。这对于了解控制系统的性能极限与对象特性之间的关系,理解设计的权衡和限制起着重要的指导作用。
1 有关基础知识
当且仅当存在多项式x(s)和y(s),使得式(1)成立时,则称多项式f(s)和g(s)是互质的。
fx+gy=1
(1)
式(1)称为Bezout等式[5]。对任意正则实有理传递函数矩阵G属于RH的八个矩阵,满足如下关系[6]:
(2)
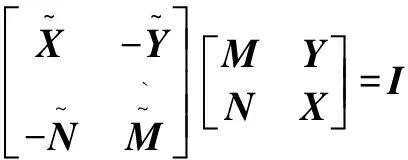
(3)
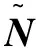
20世纪70年代后期,针对线性时不变系统,Youla等人给出了使得系统稳定的所有控制器的参数化方法,得出如下结论:对于使系统达到渐进稳定的控制器K,都可以通过Youla参数化进行分解。
2 跟踪问题描述
系统的跟踪性能通过参考输入信号和输出能量之差来衡量。假设系统的初态为零,系统的跟踪性能指标定义为:
(4)
(5)
3 最优跟踪设计
系统框图如图1所示,G(s)与K(s)分别为对象模型和控制器的传递函数,τ为网络时延,r和y分别为参考输入和系统输出,e为跟踪误差。本文将丢包的情形模拟为一个伯努利事件,用开关T来模拟反馈通道数据传输过程:当T闭合时(为1),数据成功传输,概率为Psuc;当T断开时(为0),数据丢失,概率为Pdrop,其中,Psuc=1-Pdrop。为了书写方便,令q为数据成功传输的概率。
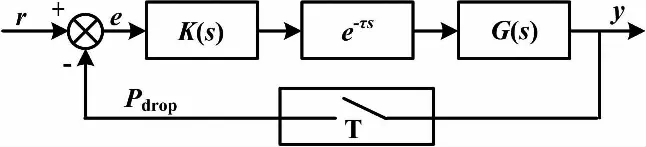
图1 具有时延和丢包的系统框图
系统闭环传递函数为:
考虑r为单位阶跃信号,即当t≥0时,r(t)=1;当t<0时,r(t)=0,则有:
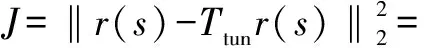

(6)
当N(s)、M(s)∈RH时,对qG(s)进行右互质分解,有:
(7)
根据全通理论,进一步分解M(s)、N(s),可得:
M(s)=Bp(s)Mm(s)N(s)=qBz(s)Nn(s)
(8)
(9)
式中:Bp和Bz为全通因子,Bp包含对象所有不稳定极点pj∈C+,j=1,…,m,Bz包含对象右半平面所有零点zi∈C+,i=1,…,n;Mm和Nn为最小相位部分。
对于任意X(s)、Y(s)∈RH满足Bezout[7],证明见Meinsma和Zwart[8]文中定理3.2。
M(s)X(s)-e-τsN(s)Y(s)=1
(10)
当Q(s)∈RH时,通过Youla参数化[7]可将所有镇定控制器的集合表示为:
(11)
由式(6)、式(7)、式(10)和式(11)可得:
(12)
为求出系统跟踪性能J的最优值,在前向通道有延迟环节的基础上[4],引入定理1。
定理1 对于图1所示网络反馈控制系统,系统的最优性能为:
(13)
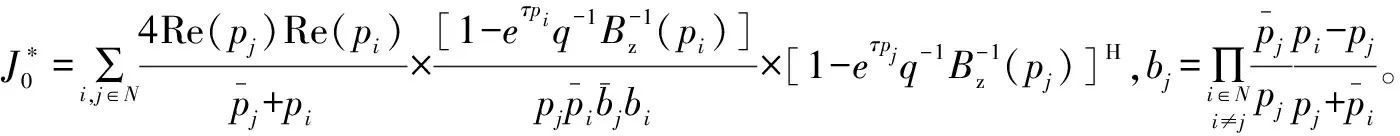
定理1证明如下。
根据式(5)和式(12)可得:
(14)
令T=eτs+q-1N(Y-MQ),则求解系统跟踪最优性能Jopt等价于求解Topt。
(15)
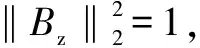
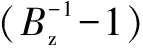
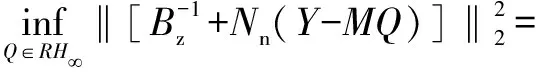
(16)
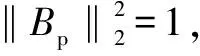
(17)
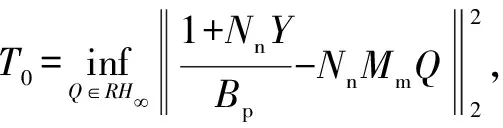
(18)
式中:L(s)∈RH;
根据Bezout等式(10),由M(pj)=0,可得:
(19)
则可得:
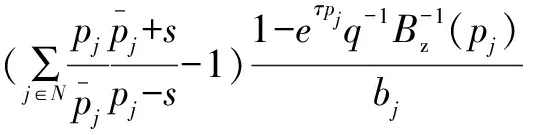
由于Nn和Mm均为外部函数和最小相位部分,因此容易得出:
(20)
至此完成定理1的证明。定理1说明考虑网络时延和数据丢包,线性时不变单输入单输出(single input single output,SISO)系统最优跟踪性能指标由控制对象的NMP零点a、不稳定极点c、网络时延τ和数据丢包概率(1-Psuc)共同决定。
4 仿真示例
考虑不稳定模型对象:
(21)
式中:a∈(0,10);c∈(0,10)。
根据定理1,系统最优跟踪性能Jopt的表达式为:
(22)
4.1 单变量研究
分别研究Jopt曲线和非最小相位零点a、不稳定极点c、网络时延τ和数据丢包概率(1-Psuc)的关系,仿真曲线如图2所示。
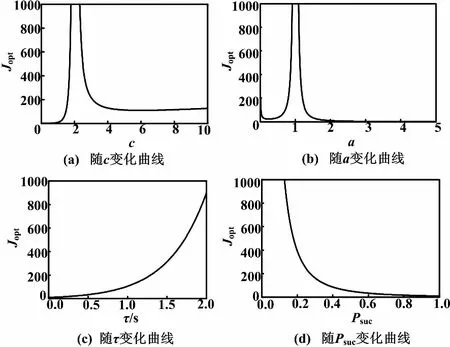
图2 最优性能Jopt随单变量变化曲线
从图2可以看出,NMP零点、不稳定极点对Jopt的影响类似,当零极点绝对值较小时,Jput随着零极点离坐标轴的距离变远而变差,较大时影响变小;存在时延的NCS,其跟踪性能随着网络时延的增加、数据丢包概率的增大而恶化,所能允许的时延和丢包有一定的范围限制。
4.2 多变量研究
考虑两个变量对Jopt的影响,分以下六种情形进行仿真研究。
① 当z1=a=2、p1=c=1时,研究Jopt和Psuc、τ的关系,仿真曲线如图3所示。
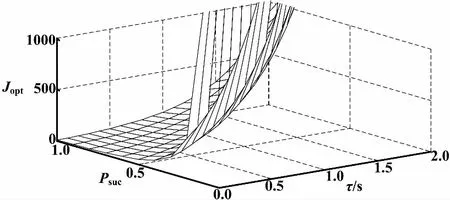
图3 最优性能Jopt和τ、Psuc仿真曲线
② 当τ=0、Psuc=1时,研究Jopt和a、c的关系,仿真曲线如图4所示。
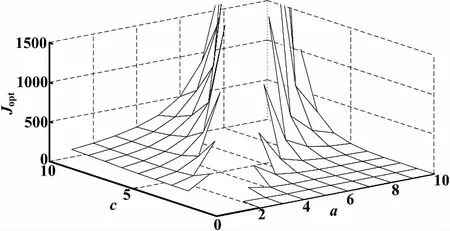
图4 最优性能Jopt和a、c仿真曲线
③ 当Psuc=1、c=1时,研究Jopt和a、τ的关系,仿真曲线如图5所示。
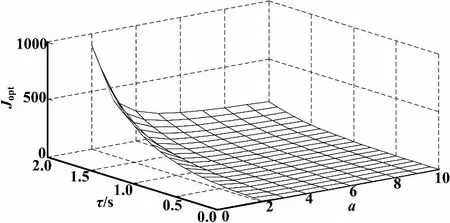
图5 最优性能Jopt和a、τ仿真曲线
④ 当τ=0、c=1时,研究Jopt和a、Psuc的关系,仿真曲线如图6所示。
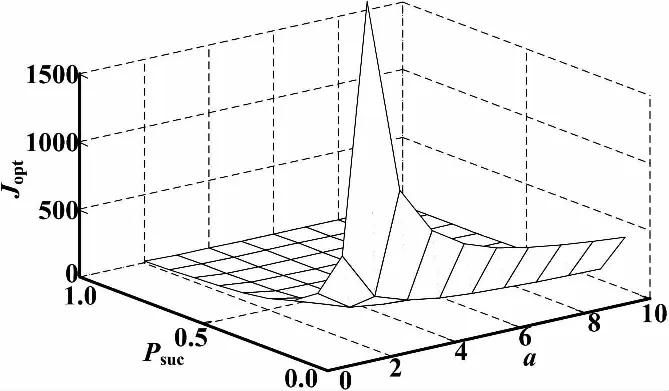
图6 最优性能Jopt和a、Psuc仿真曲线
⑤ 当Psuc=1、a=2时,研究Jopt和c、τ的关系,仿真曲线如图7所示。
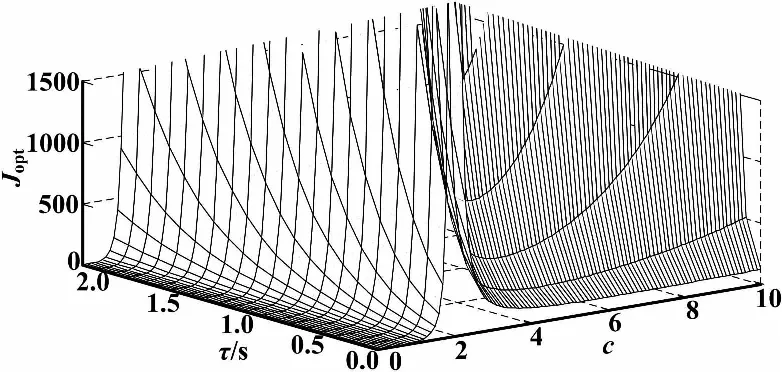
图7 最优性能Jopt和c、τ仿真曲线
⑥ 当τ=0、a=2时,研究Jopt和c、Psuc的关系,仿真曲线如图8所示。
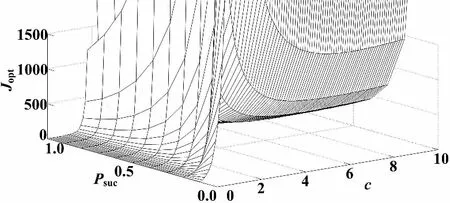
图8 最优性能Jopt和c、Psuc仿真曲线
从图3可以看出,数据成功传输的概率越大,最优性能Jopt越好,时延越大,性能越差,当数据丢包和时延超过一定范围时,性能明显变坏。图4反映了Jopt随着的NMP零点、不稳定极点离坐标轴的距离变化而变差,当零极点相消时,性能被破坏。图5和图6分别反映了NMP零点和时延、丢包的关系,图7和图8则分别反映了不稳定极点和时延、丢包的关系。图6~图8说明,当零极点为某一分布时,所能允许的时延和数据丢包均只能在某一范围内。
5 结束语
本文主要研究了网络控制系统的最优跟踪性能与网络时延、数据丢包、NMP零点、不稳定极点之间的相互关系。首先建立了系统模型,然后进行最优跟踪设计,最后通过七组仿真试验验证本文方法的有效性和可行性,表明控制对象的NMP零点、不稳定极点、网络时延和数据丢包的概率共同决定了最优跟踪性能,以及它们是如何从根本上影响最优跟踪性能的。该方法还可以推广到带宽、量化误差、信噪比、参考信号等情形。
[1] Zhao Y B,Jongrae K,Liu G P,et al.Compensation and stochastic modeling of discrete-time networked control systems with data packet disorder[J].International Journal of Control,Automation and Systems,2012,10(5):1055-1063.
[2] 朱进,王林鹏,奚宏生.转移概率未知下具有双Markov链的网络控制系统控制器设计[J].控制与决策,2013,28(4):490-494.
[3] Donkers M C F,Heemels W,Bernardini D,et al.Stability analysis of stochastic networked control systems[J].Automatica,2012(48):917-925.
[4] 詹习生,关治洪,吴博.网络化控制系统最优跟踪性能[J].华中科技大学学报,2010,38(12):49-51.
[5] Francis B A.A course in H∞ control theory[J].Lecture Notes in Control and Information Science,Springer-Verlag,1984.
[6] Walsh G C,Ye H,Bushnell L.Stability analysis of networked control systems[C]//1999 American Control Conference,1999:2876-2880.
[7] Rojas A J,Braslavsky J H,Middleton R H.Fundamental limitations in control over a communication channel[J].Automatica,2008,44(12):3147-3151.
[8] Gjerrit M,Hans Z.On H∞ control for dead-time systems[J].IEEE Transactions on Automatic Control,2000,45(2):272-285.
[9] 王后能,关治洪,丁李.脉冲干扰下网络反馈系统的性能极限[J].华中科技大学学报,2009,37(10):37-39.
[10] 姜翀.网络控制系统的建模、分析与控制[D].沈阳:东北大学,2010.
[11] Li Hongbo,Chow M Y,Qi Zengqi.Optimal stabilizing gain selection for networked control systems with time delays and packet losses[J].IEEE Transactions on Control Systems Technology,2009,17(5):1154-1162.

