高耸登机桥立柱的稳定性分析

朱新朝，顾晓勤，2，杜平安

(1.电子科技大学机械电子工程学院，四川成都 611731;2.电子科技大学中山学院，广东中山 528402)

0 引言

旅客登机桥广泛应用于各大航空机场的辅助设备，它是连接候机楼和飞机机身的一种可移动桥梁设备。如图1。登机桥主体结构由立柱、旋转平台、活动通道、接机口、升降与行走系统、服务梯等部分组成［1］。

图1 登机桥

失稳的突发性，使得稳定性计算成为钢结构设计中的重要内容。登机桥作为一种钢结构产品，它的安全可靠关系到行人和飞机的安全，特别对于A380之类的高耸登机桥，其立柱稳定性问题必需考虑。

1 登机桥力学模型

图2为登机桥的结构简图，升降系统ABC和HED上端通过高强度螺栓与活动通道相连，下端通过一个粗短柱子O1O2与行走系统铰接。旅客通过活动通道上、下飞机。活动通道两端分别与旋转平台和接机平台相连(O5O6右侧部分为旋转平台的一部分，接机平台图2中未画出)。

图2 登机桥结构简图

2 左柱稳定承载力计算

一旦登机桥右柱油缸出现故障，无油压力，左柱将承担通道的全部压力。图2中左柱DEH的结构如图3(a)，它的内导管和滚珠丝杠套在外导管内，滚珠丝杠上端部与外导管栓接，下部与内导管以丝杠螺母副的形式连接。电机带动丝杠转动，实现外导管沿内导管的上下滑动。轴向压缩弯曲小变形时外导管不承受力，左柱力学模型如图3(b)。滚珠丝杠完全伸出时，稳定承载能力最弱，以此种情况分析左柱的临界载荷。不考虑扭转的影响，丝杠螺母副连接在稳定性分析中可视为固定刚接。内导管的截面惯性矩和长度分别为I1、l1，滚珠丝杠的截面惯性矩和长度分别为I2、l2，结构所受载荷为P。设图3(b)下部的内导管轴线挠度y1，上部的滚珠丝杠轴线挠度y2，l=l1+l2。分别列挠曲线微分方程为:

其解为:

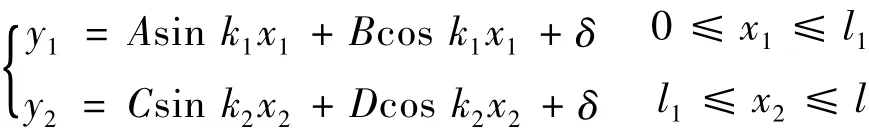
式中:

代入边界条件y1(0)=0;y'1(0)=0;y2(l)=δ;y1(l1)=y2(l1)解得:

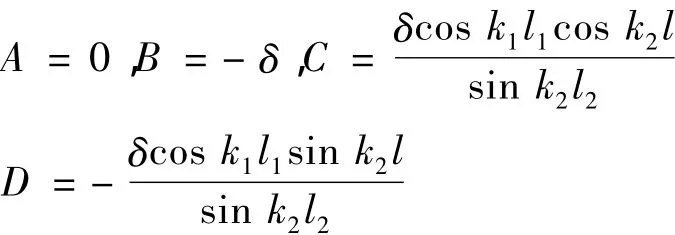
挠曲线方程为:

图3 左柱结构及力学模型图

代入y'1(l1)=y'2(l1)可得超越方程［2］为:

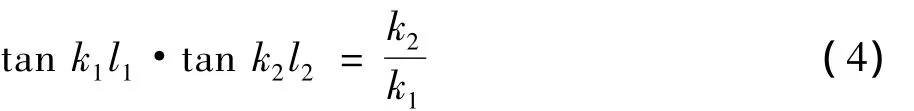
由(2)式得到k1=k2，代入式(4)，求解上述超越方程得到k2，代入式(2)得登机桥左柱临界载荷 P(即 Pcr左)。

算例1某型号登机桥:I1=6 373 cm4，I2=718.7 cm4，l1=400 cm，l2=400 cm，E=206 GPa，

(1)采用上述分析方法，联立式(4)和式(2)得Pcr左=181.8 kN。

(2)用ANSYS对内导管和滚珠丝杠套建立有限元计算模型，其中内导管为外径20 cm×20 cm，内径17 cm×17 cm的方管，滚珠丝杠直径为11 cm。分析结果如图4，临界载荷为 Pcr左=181.43 kN。

两种方法相比，误差为0.19%，说明笔者采用的理论分析计算的正确性。

当滚珠丝杠失稳后，由于外导管对滚珠丝杠变形的限制作用，左柱实际的临界载荷会比181.8 kN大。

图4 ANSYS分析结果

3 右柱稳定承载力计算

如果左柱丝杠失效不能承载，右柱将承担通道的全部压力。如图5所示。

图5 右柱结构及液压缸受力模型图

右柱ABC的结构如图5(a)，由内、外导管和液压缸组成。液压缸的伸缩运动带动外导管沿内导管的滑动。轴向压缩弯曲小变形情况下，只有导管内部的液压缸受力，所以计算右柱的承载能力即是计算液压缸的临界载荷。两端铰支的液压缸的受力模型如图5(b)，液压缸两端受到力P的作用。缸筒铰支端到活塞长度为l3，活塞到缸头为l4，缸头到活塞杆铰支端为l5，缸头的挠度为δ。计算液压缸临界载荷时，由于活塞与缸筒、活塞杆与导向套之间的间隙较小，可不予考虑。

缸筒惯性矩往往为活塞杆惯性矩的1.8～2倍，把缸筒认为刚体的刚性缸体计算法［3］已不适用，需考虑缸筒的变形。活塞杆、缸筒的受力模型如图6。

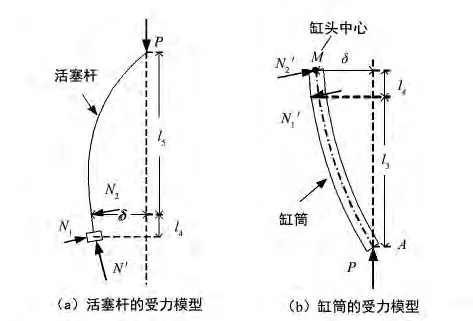
图6 活塞杆及缸筒的受力模型图

图6 中，N1、N2是活塞杆受到来自缸筒的作用力，N1'、N2'是缸筒受到的反作用力。图6(a)中，活塞杆一端受到压力P的作用，另一端受到液压油的压力N'的作用，与缸头接触处的活塞杆挠度为δ。图6(b)中，缸筒底端所受到P，对缸筒的缸头中心M取矩，可得N1=Pδ/l4。挠度方程分别为:

式中:

边界条件:y3(0)=0;y3(l3)=y4(l3);y'3(l3)=y'4(l3);y4(l3+l4)=y5(l3+l4)=δ;y'4(l3+l4)=y'5(l3+l4);y5(l3+l4+l5)=0。可解得超越方程为［4］:

联立方程(6)、(7)，解出 P，即临界载荷 Pcr右。

算例2与算例1相同的登机桥:l3=3.64 m，l4=0.36 m，l5=4 m，I3=1 286.6 cm4，I4=718.7 cm4，代入方程(7)，得到 k4=0.455，由式(6)解出 Pcr右=k24EI4=306.5 kN。

当液压缸失稳后，由于外导管对液压缸变形的限制作用，右柱实际的临界载荷会比306.5 kN大。

4 框架柱的临界载荷

以上单独分析了两柱的临界载荷，现考虑外导管的影响以及两柱之间的相互影响，模型可简化为图6所示的ABCDEH框架。此种情形为登机桥正常工作情况。

图7 立柱框架

图7 中，FO2X和FO2Z为立柱框架在O2处所受的力，用图中数字表示各个柱和梁的编号。此框架模型中，AC柱和HD柱被分为两部分，BC=ED，AB=HE，BCDE与通道固结，在计算临界载荷时只需计算AB和HE部分即可。

设杆件 j的线刚度［5］Kj=Ij/lj(j=1，2，…，7)，Ij和lj为j杆的截面惯性矩和长度，各柱上端约束参数

Kj1=∑u

Kb/∑uKc(j=1，3)，为连接于柱上端的梁的线刚度之和与柱的线刚度之和的比值，Kb、Kc均取自Kj，各柱下端约束参数Kj2=∑d

Kb/∑d

Kc(j=1，3)为连接于柱下端的梁的线刚度之和与柱的线刚度之和的比值。

由有侧移钢架柱的计算长度系数μj的实用计算公式［5］:

可得钢架柱的临界荷载:

Kj1和Kj2代入式(8)和(9)求出AB柱和HE柱临界荷载和。

算例3

与算例1、2相同的登机桥，按框架模型处理。AB和EF柱长度l1=l3=600 cm，l2=l4=l6=200 cm，l5=l7=250 cm，选用Q345钢材。对于活动通道的线刚度，算例取截面惯性矩近似为6个折弯板的惯性矩。取框架柱的截面惯性矩I1=I3=6 864 cm4，I2=I6=366 cm4，I4=23 213 cm4，I5=I7=15 252 cm4。线刚度 K1=K3=11.44 cm3，K2=K6=1.83 cm3，K4=116.07 cm3，K5=K7=61 cm3，有 K11=K31=0.025，K12=K32=10.15。把 Kj1和 Kj2(j=1，3)代入式(8)可以得出 μ1=μ3=1.91，把 μ1=μ3=1.91 代入式(9)可得临界荷载==1 062 kN。

考虑外导管和两柱之间的相互影响之后，整个登机桥框架系统的临界载荷为1 062 kN。

5 结论

可确定三种情形的临界载荷:①登机桥右柱油缸出现故障，无油压力，仅有左柱受力;②左柱丝杠失效不能承载，仅有右柱受力;③左右柱均正常工作，两柱同时受力。除了正常工作，其他二种情况，在登机桥工作时可能发生，设计计算中要给与足够的考虑。笔者提出的登机桥立柱稳定性计算方法，可为工程设计提供参考。

［1］ 顾晓勤，罗良清，袁严辉.登机桥立柱下降中通道向上收缩的分析［J］.机械设计，2013，30(6):40-43.

［2］ S.P.Timoshenko，J.M.Gere.Theory of Elastic Stability［M］.McGraw-Hill，1961.

［3］ 林荣川.液压缸的约束方式与稳定性研究［J］.机电技术，2006(3):31-33.

［4］ 郭应龙.液压缸的稳定性分析［J］.武汉水利电力学院学报，1988(2):23-33.

［5］ 陈 骥.钢结构稳定理论与设计［M］.北京:科学出版社，2008.