齿轮参数对行星轮系模态的影响

王天利，张键

(辽宁工业大学，辽宁 锦州 121001)

0 引言

机械在工作过程中产生的振动严重影响其设备的生产效率及使用寿命。同时，由于机械振动所产生的噪声对环境也会产生严重的污染。齿轮传动是各种机械设备应用最广泛的动力传动装置，而机械振动以及噪声大部分来自于齿轮在工作过程中所产生的振动。因此，研究齿轮传动系统动力学一直备受人们的关注［1－3］。利用有限元法对齿轮系统结构形式、几何参数进行深入的研究，可以设计与制造高品质的齿轮传动系统。使用Catia 行星轮系进行实体建模，利用Workbench 设置单元、材料属性、自由度约束以及有限元分析计算，得到行星轮系的固有频率和振型，并进一步分析模数以及压力角变化对行星轮系模态的影响。通过模数以及压力角的变化对行星轮系的结构振动特性分析，对于提高行星轮系的安全性和可靠性具有重要的意义［4－5］。

1 单个行星排的传动方案

根据输入轴、输出轴和固定轴的不同选择，可以获取6 种不同的传动方案。如表1 所示。单个行星排的传动比方案不同，约束也不同。一般行星齿轮机构用来实现减速传动，而且要求传动比比较大，因此选择A 方案，然后根据行星轮系实际传动情况，对行星轮系进行施加约束并进行模态分析。

表1 单个行星排的传动比方案

2 行星轮系模态分析

2.1 模态分析理论基础

模态分析是动力学分析重要的理论基础，主要用于确定机械结构和部件的固有频率、固有振型、模态刚度、模态质量和模态阻尼，是谐响应分析、瞬态动力分析和谱分析的开端。

一个N 自由度的线性系统，其振动微分方程为［6］:

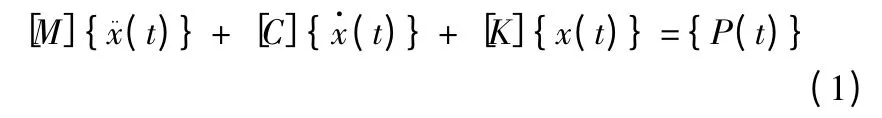
式中:［M］、［C］、［K］分别为质量矩阵、阻尼矩阵、刚度矩阵;{P(t)}为激振力向量;{x··(t)}、{x·(t)}、{x(t)}分别为加速度向量、速度向量、位移向量。

要对行星系统进行模态分析，求解的主要是固有频率和振型参数固有模态，由于固有频率与外载荷无关，故可令激振力等于0;且当结构阻尼在很小的情况下，阻尼对固有频率的影响比较小，基本上可以不考虑，因此可以简化成结构无阻尼自由振动方程计算结构的固有特性，由式(1)可得:

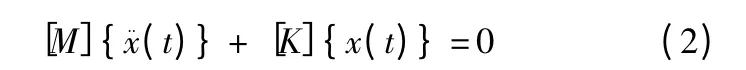
其对应的特征方程为:

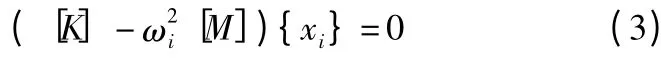
由式(3)可得出n 个特征值，也就是结构的n 阶固有频率ωi2和相应的n 个特征向量也就是结构的模态振型{ φ}i，它反映了结构按频率ωi振动时各自由度方向振幅间的相对比例关系。

2.2 有限元分析模型

使用Catia 对行星轮系进行参数化建模，模型主要参数:太阳轮齿数、行星轮齿数、齿圈齿数分别为22，23，68，行星轮数目为3，齿轮模数都为3 m，压力角都为20 °。在Catia 中建立的行星轮系模型只是实体模型，而实际分析中针对的是有限元模型，如图1 所示。因此需要对实体模型进行单元定义和网格划分。

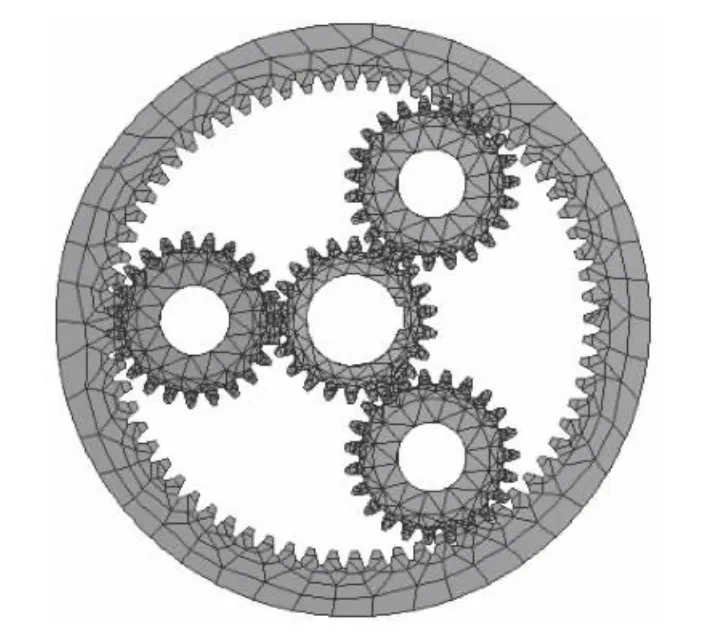
图1 行星轮系有限元模型

齿轮的材料为铬锰合金钢20CrMnTi，其弹性模量为2.06 × 105MPa，泊松比取值0.3，密度为7.8 × 10－9g/mm3。

对行星轮系所有齿轮的齿部以外采用以六面体单元为主进行网格划分，齿轮齿部则用四面体单元。这样既对重要部分可以进行精确的求解，而又不会使整个有限元模型网格较多导致计算时间太长。

2.3 行星轮系有限元模型中的自由度约束

1)行星轮系有限元模型的自由度约束

模态分析是在初始约束状态下求解系统的固有频率和振型，故需要对模型的初始状态进行约束，包括1 个太阳轮，3 个行星轮和1 个内齿圈的初始状态约束。

对于太阳轮，约束其中心孔内的所有节点的ux，uy，uz方向的自由度。

对于行星轮，需要建立局部柱坐标系，如图2 所示，坐标系的原点设置在各个行星轮的中心处。设置完成后，激活局部柱坐标系，然后约束中心孔处所有节点的ux，uy(uz)方向的自由度。

对于内齿圈，则是完全约束齿圈外部所有节点的自由度［7］。

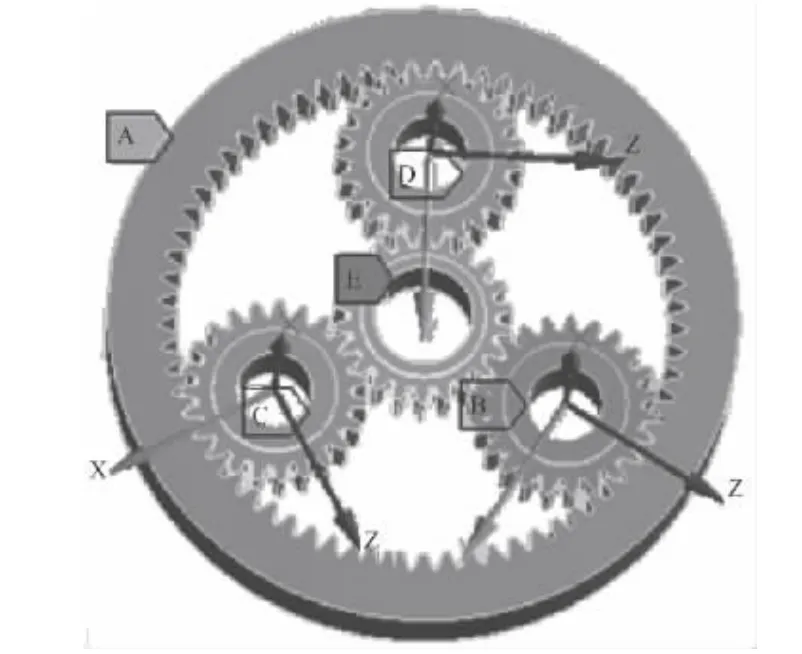
图2 轮系的自由度约束

2)啮合齿轮间耦合关系的设定

在整个分析过程中，定义齿轮间的接触关系是非常重要的，齿轮在啮合的过程中齿廓间产生作用力，故采用定义齿轮间的无摩擦接触关系的方法来模拟实际啮合以便达到简化分析的目的。主要对整个行星齿轮系统的啮合施加接触约束，即行星轮和内齿圈之间的接触，太阳轮和行星轮之间的接触，如图3 所示［8］。

图3 耦合约束

2.4 模态分析求解

模态分析是采用试验分析或理论分析的方法来识别系统的模态参数，为系统结构动力学分析、振动故障诊断及结构的动力特性的优化设计提供依据。

在ANSYS 软件中，模态提取算法主要有Sub－space，Block Lancos，Power Dynamics，Reduced，Damped 等。考虑到Block Lancos 算法的求解精度高，计算速度快，故对行星轮系采用BlockLancos 算法进行模态分析。计算时提取模态数为前9 阶模态振型及固有频率(表2)，各阶模态振型如图4(a)图4(c)所示［9］。

图4 各阶模态振型图

表2 行星轮系前9 阶固有频率

第一到第六阶固有频率对应振型是三个行星轮的扭转振动，振幅明显有增大的趋势。第七到第九阶固有频率对应振型分别是不同一个行星轮的摆动振型。

3 齿轮模数的变化对模态的影响

模数是指相邻两轮齿同侧齿廓间的法向齿距t 与圆周率π 的比值(m=t/π)，以mm 为单位。模数是齿轮的一个最基本参数。模数越大，轮齿越高而且越厚，如果齿轮的齿数一定，则齿轮的径向尺寸就越大。分别取模数为2 mm，3 mm，4 mm，其他参数不变。然后通过对行星齿轮进行动力学模态分析，确定模数的变化会对整个行星轮系的模态有何影响。

通过有限元分析得出在不同模数下的固有频率及振型。由于篇幅有限，振型图不再列出，通过表3 来比较在不同模数下对固有频率的影响。

通过表3 和图5 可以明显看出，模数的变化对行星轮系的固有频率有一定的影响，并且整个行星轮系的固有频率随着模数的增大而减小。

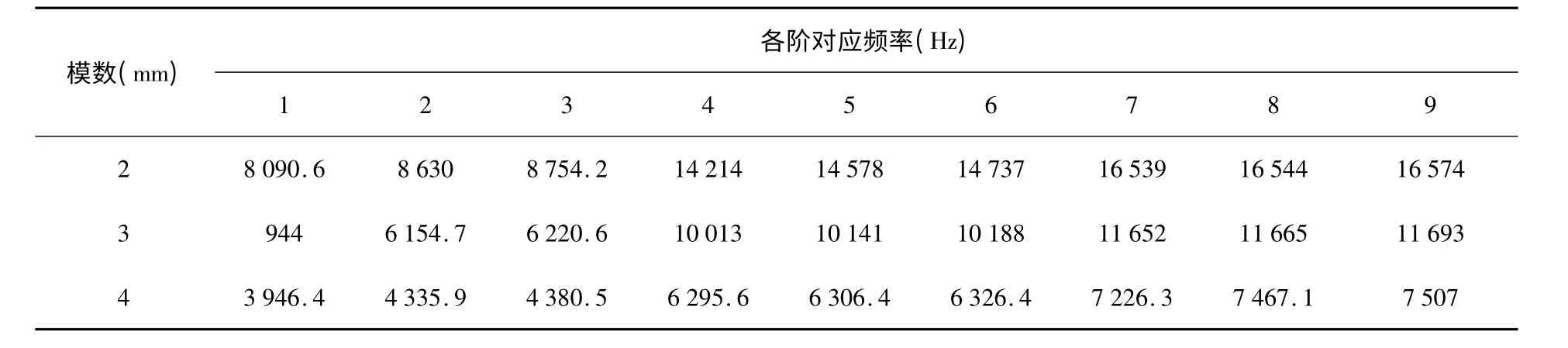
表3 模数分别为2 mm、3 mm、4 mm 的行星轮系的前9 阶固有频率

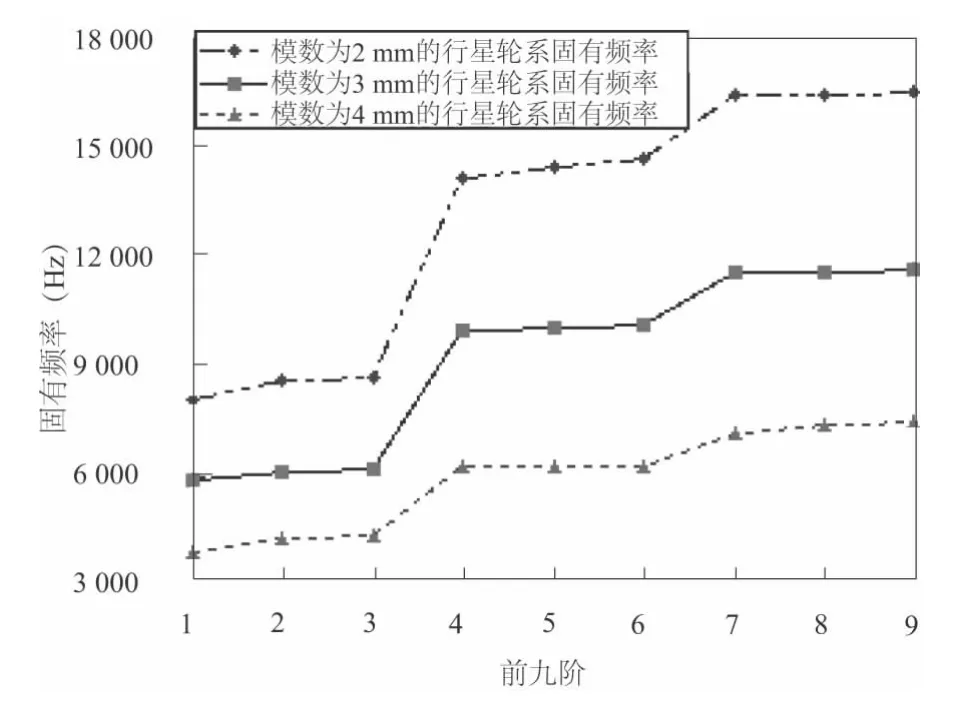
图5 不同模数的行星轮系固有频率值对比图

4 齿轮压力角变化对模态的影响

压力角又称啮合角是在两齿轮节圆相切点P 处，两齿廓曲线的公法线(即齿廓的受力方向)与两节圆的公切线(即P 点处的瞬时运动方向)所夹的锐角。对单个齿轮而言称作齿形角。标准齿轮的压力角一般为20°。小压力角齿轮的承载能力较小，而大压力角齿轮，虽然承载能力较高，但在传递转矩相同的情况下轴承的负荷增大，所以仅用于特殊情况。分别以压力角为18°、20°、22°，其他参数不变。然后通过对行星齿轮进行动力学模态分析，确定压力角的变化会对整个行星轮系的模态有何影响(表4)。

通过表4 和图6 可以明显看出，压力角的变化对行星轮系的固有频率有一定的影响，并且整个行星轮系的固有频率随着压力角的增大而增大。

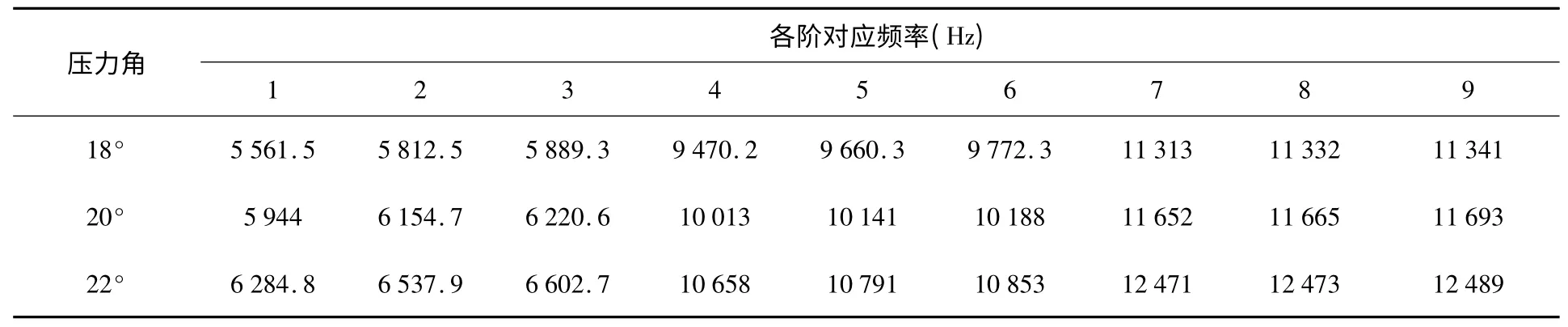
表4 压力角分别为18°、20°、22°的行星轮系的前9 阶固有频率

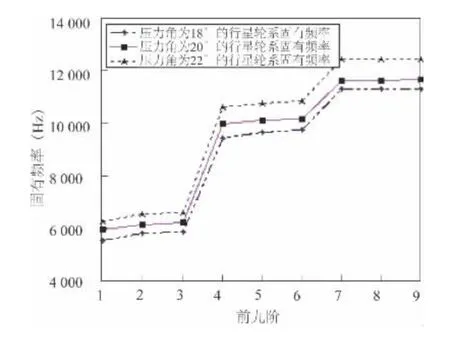
图6 不同压力角的行星轮系固有频率值对比

5 结论

本文利用有限元软件ANSYS Workbench 对行星轮系进行了模态分析，提取了行星轮系的前9 阶固有频率和振型;在其他参数不变情况下，改变齿轮的模数，通过有限元分析表明整个行星轮系的固有频率随着模数的增大而减小;在其他参数不变情况下，改变齿轮的压力角，通过有限元分析表明整个行星轮系的固有频率随着压力角的增大而增大;通过对行星轮系齿轮和对行星轮系齿轮几何参数的研究，为行星轮系的结构设计提供直接的理论依据。

［1］Ahmet Kahraman.A Kinematics and Power Flow Analysis Methodology for Automatic Transmission Planetary Gear Trains［J］.Journal of Mechanical Design，2004，126(6):1071－1081.

［2］Ahmet Kahraman.Free Torsional Vibration Characteristics of Compound Planetary Gear Sets［J］.Mechanism and Machine Theory，2001，36:953－971 .

［3］李润方，王建军.齿轮系统动力学［M］.北京:科学出版社，1997:1-5.

［4］万凯宇.行星齿轮传动系统动力学分析研究［D］.南京:南京航空航天大学，2004:3-7.

［5］陶泽光，李润方，林腾蛟.齿轮系统有限元模态分析［J］.机械设计与研究，2000(3):45-46.

［6］傅志方，华宏星.模态分析理论与应用［M］.上海:上海交通大学出版社，2000:35-37.

［7］盛冬平.基于ANSYS 的行星齿轮系统参数化建模与模态分析研究［D］.南京:南京航空 航天大学，2008:29-30 .

［8］李润方，韩西，林腾蛟，等.齿轮系统耦合振动分析与实践研究［J］.机械工程学报，2000，36(6):78-81.

［9］小飒工作室.最新经典ANSYS 及Workbench 教程［M］.北京:电子工业出版社，2004.62-65.