基于网格分布的加权质心定位算法研究
, ,,
(郑州轻工业学院,郑州 450002)
无线传感器网络(Wireless Sensor Network,WSN)是由大量部署在监测区域的传感器节点组成的,通过无线通信形成一个多跳的自组织网络,协作感知,采集和处理相关监控信息[1]。无线传感器网络是面向事件的监测网络。在大多数应用中,位置信息对于感知和采集到的信息来说至关重要。如果不知道其感知对象的位置,则所感知的信息往往是毫无意义的。实时确定事件发生的位置或获取消息的节点位置是传感器网络的基本功能之一,也是提供监测位置信息的前提。因此,定位技术对传感器网络应用的有效性起着关键的作用。
无线传感器网络节点定位机制从定位手段上可分为基于测距定位[2]和非测距[3]定位。前者通过测量节点间的距离或者角度信息(信号到达时间、信号到达时间差、信号到达角度、信号强度等),使用三边测量、三角测量或最大似然估计法来计算未知节点的位置。基于测距的算法存在需要专用硬件,使传感器节点成本和体积加大的缺点,从而限制了其可用性。非测距定位不需要测量节点与信标节点间的距离或角度,仅仅依靠网络的连通度即能完成定位,其在功耗、环境及成本方面的优势,在大规模无线传感器网络定位中得到了广泛的关注。典型的非测距方法有质心算法[4]、凸规划法[5]、APS定位算法[6]和APIT算法[7]等。
不同的信标节点布局对相同节点定位的精度可以相差很大,具体来说,当未知节点离信标节点较近时,定位精度较高;反之,定位精度则较低。信标节点分布不匀会造成空洞等问题。因此,本文采用网格结构的形式来部署网络,以便对网络中大部分的节点都有较高的定位精度。
本文对加权质心定位算法的定位误差进行分析,得出环境温湿度、反射、多径、物体移动等因素对用RSSI测距技术计算出的权值误差的影响导致的最终定位误差;提出基于网格分布的自适应校正的加权质心定位算法,利用由离未知节点最近的信标节点所确定的误差因子,修正利用RSSI测距技术求出的测距值,使未知节点适应自身所处的环境,减小因为环境造成的测距误差,从而对权值进行修正。
1 加权质心算法模型
假设网络中的第n个固定信标节点Bi已知位置坐标为(Xi,Yi),其中l≤i≤n,未知节点M的估测位置坐标为(Xe,Ye)。
则加权质心算法的计算公式为
(1)
式中:Wi表示每个固定信标节点的权值。通常该权值是未知节点到固定信标节点距离的函数。如果未知节点不能与固定信标节点Bi通信, 那么Wi为零[8]。
1.1 加权质心算法中的权值计算
对于n个固定信标节点B1(X1,Y1),B2(X2,Y2),…,Bn(Xn,Yn),未知节点M(Xe,Ye)到各节点的距离分别为d1,d2,d3,…,dn。
首先,只考虑两个节点B1、B2。假设两节点的质心在B12,位置为(X12,Y12),B12到B1和B2的距离分别为d1,d2,则存在
(X12-X1)/d1=(X2-X12)/d2
(Y12-Y1)/d1=(Y2-Y12)/d2
由此可得
X12=(X1/d1+X2/d2)/(1/d1+1/d2)
Y12=(Y1/d1+Y2/d2)/(1/d1+1/d2)
所以,可以简单地假设1/di为权值。这样选择加权因子能够体现各个节点对于未知节点的决定权大小,其约束力符合加权质心算法的要求[9]。
1.2 无线电传播路径损耗模型的分析
无线电信号在空间传播时会有不同程度的损耗, 这些损耗在很大程度上影响了基于RSSI算法的定位精度, 因而选取合适的损耗模型尤为重要。这里采用自由空间传播模型和对数-常态分布模型,对整个环境进行仿真模拟。
自由空间无线电传播路径损耗模型为
LOSS=32.44+10klgd+10klgf
(2)
式中:d为测点距信源的距离, 单位为km;f为频率, 单位为MHz;k为路径衰减因子。其他模型模拟现实环境,但与现实环境还有一定差距。对数-常态分布模型的路径损耗计算公式为
PL(d)=PL(d0)+10klg(d/d0)+X0
(3)
式中:X0是平均值为0的高斯分布随机变数, 其标准差范围为4~10;k的范围在2~5之间。取d=1, 代入式(2),可得LOSS的值。此时,各未知节点接收信标节点信号时的信号强度为
RSSI测量值=发射功率+天线增益-路径损耗(PL(d))
(4)
通过式(2)、(3)、(4)可以得到距离di,从而通过加权质心算法实现定位[10]。
2 自适应校正的加权质心算法
加权质心定位算法采用RSSI测距来估计节点间的距离,这种方法不需要信标节点的硬件改动。但是,因为RSSI测距往往存在不精确的问题,所以算法中的RSSI测距在定位中不直接用来定位计算,而只是用来进行计算加权质心算法的权值参数,算法的本质还是基于Range-Free的定位。尽管RSSI测距没有直接用于定位计算,但它存在的误差对算法的定位精度依然产生着重要的影响。首先分析测距误差给加权质心定位算法造成的影响,然后用自适应校正的算法来降低这种影响。
2.1 修正因子αij的计算

本文将离未知节点最近的信标节点作为参考节点,用参考节点的校正因子修正未知节点的测距。修正后的测距量比原始测距量能更精确地反映节点间的远近关系,从而使权值更符合理想测距情况下加权质心算法的要求,达到了提高定位精度的目的。

图1 自适应修正测距误差的示意图
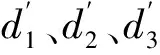
αij≈βij
(5)

(6)
假设每个未知节点都有一个邻近信标节点作为自适应校正参考节点,使得该节点的通信范围存在同一组信标节点,并能够对这组信标节点分别测距,那么,自适应修正后的加权质心定位算法为
(7)
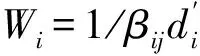
2.2 自适应校正加权质心定位算法的定位
(1)信标节点周期性发送自身节点ID和自身位置信息。
(2)未知节点在收到信息后,多次记录RSSI值,然后求均值。
(3)未知节点在收到超过阈值的n个信标信息后,建立以下4个集合:
①信标节点集合:Sn={a1,a2,a3,… ,an};
②未知节点到锚节点的距离集合:Dn={d1,d2,d3,…,dn};
③校正因子集合:Bn={β1,β2,β3,…,βn};
④信标节点的位置坐标:Pn={(x1,y2),(x2,y2),(x3,y3),…,(xn,yn)}。
(4)根据式(6)计算出每个信标节点的加权值ωi。
(5)根据式(7)计算出未知节点的位置坐标(Xe,Ye),该坐标就是经过自适应校正加权质心算法定位出的未知节点的坐标。
改进的自适应定位算法的定位流程如图2所示。
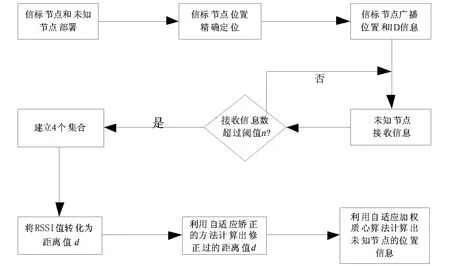
图2 自适应定位算法的节点定位流程图
3 仿真实验与分析
3.1 仿真实验
为了对改进算法的有效性和可用性进行验证,我们使用Matlab先后对传统质心定位算法和自适应校正的加权质心算法进行仿真比较和仿真实验,并对仿真结果进行分析。对环境模型做如下设置:假定环境是在一个自由空间环境中进行的,模拟环境为一个100 m×100 m的区域,按照网格型部署信标节点,未知节点则通过随机的方式产生,分布如图3所示。

图3 锚节点分布图
为了衡量定位算法的有效性,本文将定位误差作为评价定位技术的首要指标。定位误差一般用误差值与节点通信半径的比例表示。定义为
(8)

(9)
信标节点按100 m×100 m的结构分布,未知节点为30个,节点的通信半径设为20 m,然后根据式(2)、(3)、(4)生成的RSSI数据,在数据中添加均值为0,方差为7的高斯噪声来代替实际环境中的反射、多径和物体移动、气候等带来的影响,衰减系数N取3,再通过自由空间传播模型和对数-常态分布模型,按照上述步骤来仿真定位。对传统质心定位算法和自适应校正的加权质心算法反复实验,求出平均定位误差(见图4、图5)。

图4 传统质心定位算法的定位仿真图
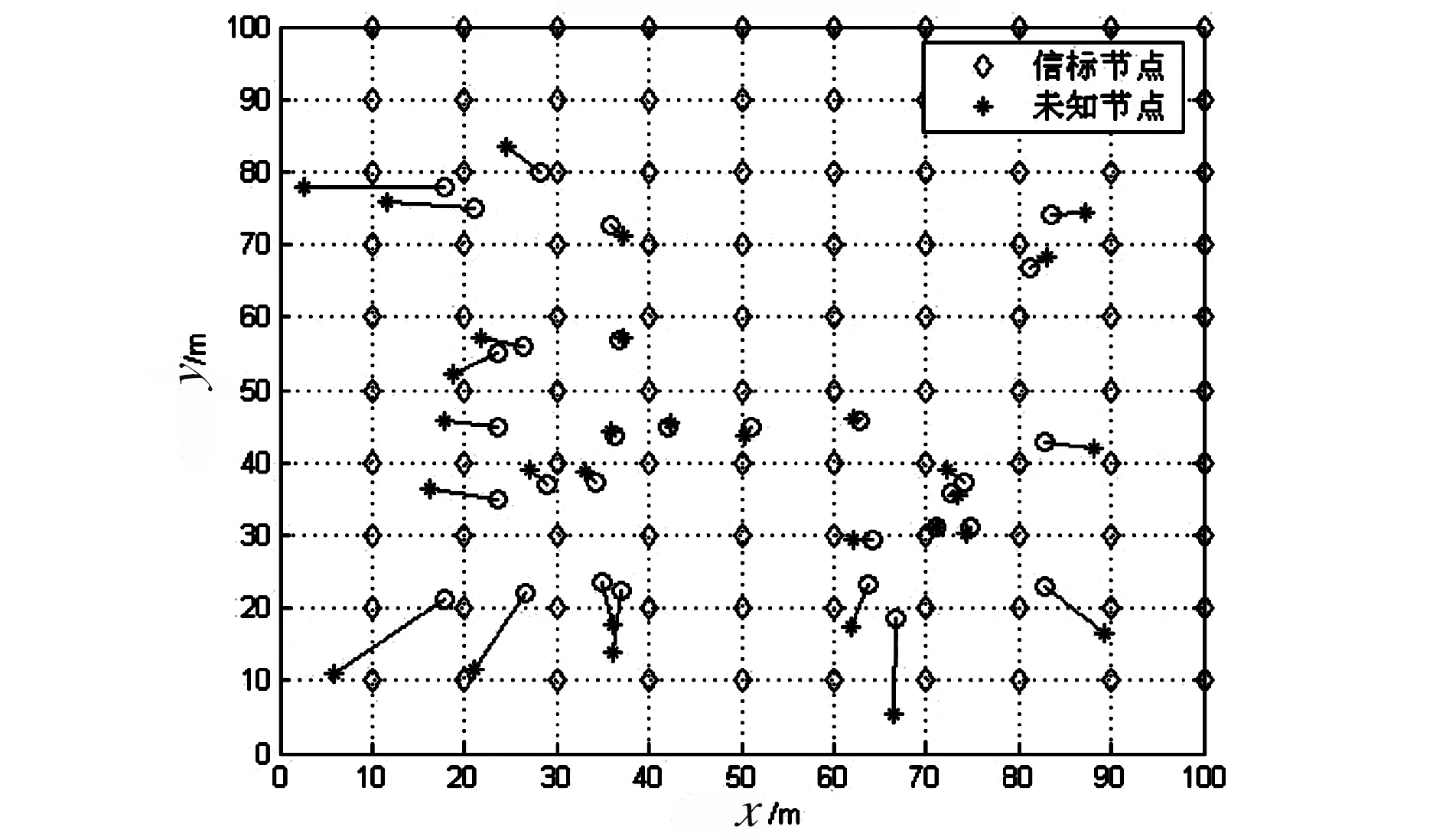
图5 自适应加权质心定位算法的定位仿真图
3.2 实验结果分析
由图4和图5可以看出,在锚节点分布均匀,锚节点比例较高的情况下,质心定位算法和自适应校正的加权质心定位算法都能实现未知节点的自定位,但是在边界处,由于锚节点只存在于未知节点的一侧,导致边界处未知节点的定位误差高于定位区域中间的未知节点。从图6和图7可以看出,大部分节点的定位精度都得到了提升。由式(8)计算出的自适应校正加权定位算法的平均定位误差相对于传统质心定位算法提高了10.9%。自适应校正的加权定位算法基本上可以准确地定位出定位节点的位置,能够满足传感器网络的一般应用要求。
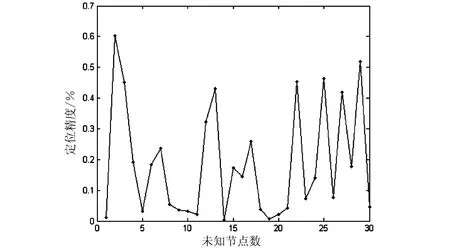
图6 传统质心定位算法各未知节点的误差图

图7 自适应校正的加权质心定位算法各未知节点的误差图
由图8可以看出,随着锚节点通信半径的增大,两种定位算法的定位精度都在减小,并且趋于稳定。这是因为随着通信半径的增大,更多的锚节点会参与到未知节点的定位过程中,以锚节点为顶点的多边形质心能够更好地代替未知节点的位置。但是在通信半径增大到一定值时,定位误差对通信半径变化的影响就不太明显了,并且通信半径过大会造成能耗的增大,减小锚节点的生命周期。所以,通信半径应该根据当时的应用要求和环境来适当选取。在相同条件下,自适应加权定位算法的定位误差明显小于传统质心定位算法和加权质心定位算法。自适应加权质心定位算法比加权质心定位算法的定位误差降低了约31.3%。

图8 定位算法的误差仿真图
4 结 语
本文提出了自适应加权质心定位算法,将测距得到的RSSI值通过离未知节点最近的锚节点进行修正,并使用Matlab软件对该算法进行了仿真实验分析。结果表明,此算法在不增加额外硬件的前提下,以增加较小的计算量为代价,提高了节点的定位精度,可以满足大多数无线传感器网络节点定位的需求。
参考文献:
[1] Tetsushi L. An Overview of the Sensor Networks[J].Transaction on Electronics,Information and Systems,2008,128(10):1498-1503.
[2] Zhang Yuan,Wu Wen-wu,Chen Yue-hui. A Range-based Localization Algorithm for Wireless Sensor Networks[J]. Journal of Communication and Networks,2005,7(4):429-437.
[3] He Qin-bin, Chen Fang-yue,Cai Shui-ming,et al. An Efficient Range-free Localization Algorithm for Wireless Sensor Networks[J].Science China Technological Sciences,2011,54(5):1053-1060.
[4] 何艳丽.无线传感器网络质心定位算法研究[J].计算机仿真,2011,28(5):164-167,219.
[5] 张翰,刘峰.无线传感网络基于凸规划的改进定位算法:Convex-PIT[J].传感技术学报,2007,20(5):1129-1133.
[6] 刘影,钱志鸿,刘丹,等.基于几何学的无线传感器网络定位算法[J].光电子激光,2010,21(10):1435-1438.
[7] 周四清,陈锐标.无线传感网络,APIT定位算法及其改进[J].计算机工程,2009,35(7):87-89.
[8] 陈维克,李文峰,首珩,等.基于RSSI的无线传感器网络加权质心定位算法[J].武汉理工大学学报,2006,30(2):265-268.
[9] 张婵爱,马艳艳,白凤娥,等.基于RSSI的加权质心定位算法的实现[J].太原理工大学学报,2009,40(2):146-147.
[10] 任维政,徐连明,邓中亮.基于RSSI的测距差分修正定位算法[J].传感器学报,2008,21(7):1247-1250.

