灰色模型与回归模型在城镇基准地价评估中的比较

刘丹阳

(中国矿业大学 管理学院，北京 100083)

一、引 言

基准地价可以反映一个区域土地市场地价的总体水平和在一段时间内的变化趋势,为国家征收土地税收提供依据[1]。基准地价是在城镇规划区范围内，对现状利用和规划利用条件下不同级别的土地或者土地条件相当的地域，按照商业、住宅、工业等用途，分别评估确定的某一时点上正常市场条件下一定年期的土地使用权区域平均价格[2]。

目前，我国基准地价评估体系趋于标准化,基准地价内涵的统一加强了其评估结果的准确性与可比性[3]。目前较为常见的城镇基准地价评估方法主要有：市场比较法﹑收益还原法、剩余法和成本逼近法、样点地价平均法﹑回归模型法﹑灰色预测模型法等。近年来，国内许多研究绕开土地定级从而直接评估基准地价，降低主观因素，使评价结果能体现市场化和准确性。刘耀林、焦利民探讨了人工神经网络应用于基准地价评估的可行性,针对基准地价评估提出了相应的人工神经网络模型和算法改进措施,以及在采用神经网络的前提下,进行土地定级与基准地价评估的新思路[4]。王伟、漆炜用矢栅混合模型划分评价单元，对地价样点进行趋势面分析筛选，使用最短路径距离代替欧氏距离对地价样点进行空间插值，叠加分析后得到各评估单元的指标地价，用其代替传统的因素综合得分对基准地价评估区域分等定级，同时测算出各级别基准地价[5]。易嗣鑫采用K-均值聚类法对基准地价更新和土地定级的方法进行探讨和研究,完善目前土地定级中级别划分方面存在的不足,加大级别划分的精确程度[6]。

本文以沁阳市为例，建立灰色模型和回归模型，结合收益还原法分别计算相应模型的基准地价。通过对两种计算模型得到基准地价进行比较，进一步表明灰色模型在基准地价评估中，计算过程便捷，计算结果可信度更高。

二、研究区域概况

(一)区域概况

沁阳市地处河南省西北部，东隔丹河与焦作市相望，北倚太行山与山西省晋城市接壤，西与济源市毗邻，南与温县和孟州市相连，总面积为602.27km2。现辖六镇、六乡和四个办事处，总人口为46.7万人。

沁阳市地处太行山南麓、黄土高原和华北平原交界处。境内地势北高南地，西高东低，由西北向东南倾斜，地形变化较大，土壤与地貌类型多样，属暖温带大陆性季风型气候，气候温和，四季分明，雨热同季，春暖而干旱，夏热而多雨，秋清而气爽，冬冷而鲜雪，年平均气温为14.3℃，水资源丰富，水质较好。

沁阳市区是在旧城的基础上发展起来的。新中国成立前，旧城虽有一定的规模，但由于道路狭窄、路面不平、基础设施差等限制了城市的发展。新中国成立后，随着本市社会、经济和文教卫生事业的快速发展，市政府不断加大对市政基础设施建设的投资力度，城市建设规模逐年扩大，基础设施和公用设施不断完善。

(二)研究区域城镇土地定级工作情况

城镇土地定级是根据城镇土地的经济、自然两方面属性及其在社会经济活动中的地位、作用，对城镇土地使用价值进行综合分析，通过揭示城镇内部土地质量在不同地域的差异，评定城镇土地级。土地级反映的是城镇内部土地质量的差异[7]。

本研究采用多因素评价法，首先依据多个影响土地级别因素、因子的影响程度、影响范围和影响方式，采用格网法划分土地定级单元，由计算机自动计算各定级因素、因子在每个定级单元的作用分值，采用等值线法、晕线法等计算机制图技术，自动绘制土地定级因素、因子作用分值图；然后按照土地定级因素、因子对土地级别影响程度的差异，以权重值量化其影响强度，并采用空间数字叠置技术，即经过加权求和的方式，自动计算定级区域内各定级单元的所有定级因素、因子的综合作用分值；最后运用频率直方图分析方法，分析确定土地定级因素因子综合影响强度的空间分布和分异规律，初步划分综合、商服、住宅、工矿仓储、公共管理与公共服务用地、交通、水利设施、特殊用地的土地级别，经专家评议、级别验证和实地踏勘，并依据土地级别划分的基本原则，最终确定各用地类别的土地级别[8]。

本研究主要以沁阳市商服用地为研究对象。根据沁阳市的实际情况，通过多因素评价法，将沁阳市商服用地分为5个级别，从优到劣，从1级到5级顺序排列。市区商服用地以第1级别为主，因此模型的建立以该级别用地内具有代表性的商场的年纯收益为基础进行分析。

三、评估模型建立

(一)灰色模型实证分析

1.灰色模型分析概述

灰色理论将客观世界划分为3种系统：白色系统——系统内部信息完全充分；黑色系统——外界对系统内部信息一无所知；灰色系统——系统内一部分信息是已知的，另一部分信息是未知的，其各因素间关系具有不确定性[9]。

商服用地的纯收益系统中，信息一部分明确而另一部分不明确，与上述第三种灰色系统的特征符合。因此，可以建立灰色模型预测研究区域商服用地纯收益。首先，建立GM(1，1)模型一阶微分方程，运用数学运算预测纯收益；利用后验差检验方法检验模型预测值的精度和可靠性，从而得到所需年份的相应样点的纯收益。

2.基准地价灰色模型的构建原理

灰色系统是通过一定的数学方法处理原始信息数据序列，然后将其转化为微分方程。基本过程如下：

(1)数据处理

根据前n年的商服用地主要的纯收益数据组成原始序列：

(1)

式中，x(0)(i)为第i年样点纯收益原始数据；x(1)(k)为k个年份纯收益数据的一次累加值，即x(0)(i)的逐年累计总量。

(2)求系数向量

首先，构建GM(1，1)模型来反映纯收益的变化趋势，其单变量线性一阶动态微分方程公式为：

(2)

式中，a为发展系数；t为时间；b为灰色作用量。

(3)根据所求得系数向量，需要构造数据向量YN为：

YN=[x(0)(2),x(0)(3),…,x(0)(n)]T

(3)

式中，n为年份。

(4)GM(1，1)模型时间响应函数为：

(4)

时间响应序列公式为：

(5)

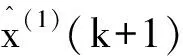
(5)还原纯收益值

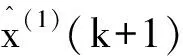
(6)

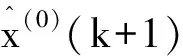
3.灰色模型检验

本研究利用后验差检验方法检验所建立GM(1，1)模型预测值的精度和可靠性。设C与p是后验差检验的2个重要数据：C为后验差比值，p为小误差率。

(7)

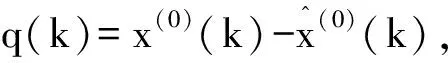
后验差比值越小表明模型计算值与实际值之差离散度越低，原始数据离散度高；小误差率越大表明残差与残差平均值之差小于给定值点较多。根据C与p两个计算指标，综合评定预测模型的精度并将预测精度分为4种类型(见表1)。

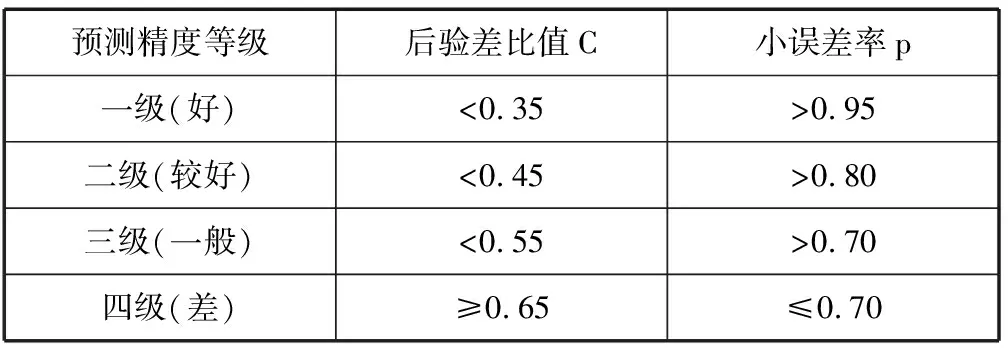
表1 预测精度类型

4.纯收益测算及精度检验

整理和修正研究区域第1级别商服用地中几个较大型商场年纯收益数据(2009～2012)，选取该级别商服用地10个样点，前4a各年份的商服用地样点平均纯收益数据，通过上述公式(5)对实际纯收益进行测算。

实际纯收益x(0)(i)及对x(0)(i)作一次累加，生成x(1)(k)(见表2)。

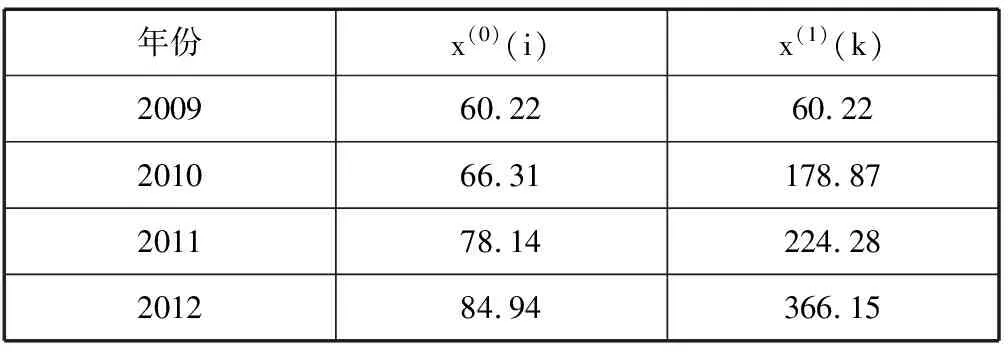
表2 样点各年份平均实际纯收益 (元/m2)

计算得到灰色参数为：a=-0.051773;b=2 452.170932

在公式6中代入a和b值，得到收益预测方程：

根据公式(6)依次代入k值，进行累减还原后，求得所对应年份的预测纯收益值(见表3)。

表3 平均样点纯收益 (元/m2)

以2009年为基准年，运用灰色模型进行样点平均纯收益预测，运用收益还原法计算第1商服用地样点平均地价2010年为909.16元/m2；2011年为1054.96元/m2；2012年为1127.44元/m2。

计算得到S1=398.26；S2=16.73；因此C=0.0772<0.35；p=1。该结果表明灰色模型预测得到第1商服用地样点纯收益符合一级精度标准。

(二)回归模型实证分析

1.回归模型分析概述

该部分是基于商服用地地价与其繁华影响度、道路通达度、人流量等内在影响因素存在着一定的相关性。因此，在建立地价与上述因素相关的数学模型时，需对其内在影响因素各指标进行量化[13]。在城镇地价定级的成果的基础上，测算划分单元地价总分值，建立商服用地价格与其相关各因素的回归模型，对商服用地基准地价进行测算。

2.回归模型构建原理

根据上述理论和思路，建立反映商服用地价格与其内在影响因素之间关系的数学方程，本研究选择的回归模型为：线性模型：Y=a1X+b1；对数模型：Y=a2ln(X)+b2；乘幂模型：Y=a3Xb3；指数模型：Y=a4eb4X；多项式模型：Y=a5X2+b5X+c。所有建立模型中，Y为商服用地样点单元基准地价；X为商服用地定级划分单元总分值。

3.回归模型的建立

根据前面假设的5种回归模型，将2009～2012年第1级别商服用地样点平均地价和划分单元定级总分值进行拟合(见表4)。

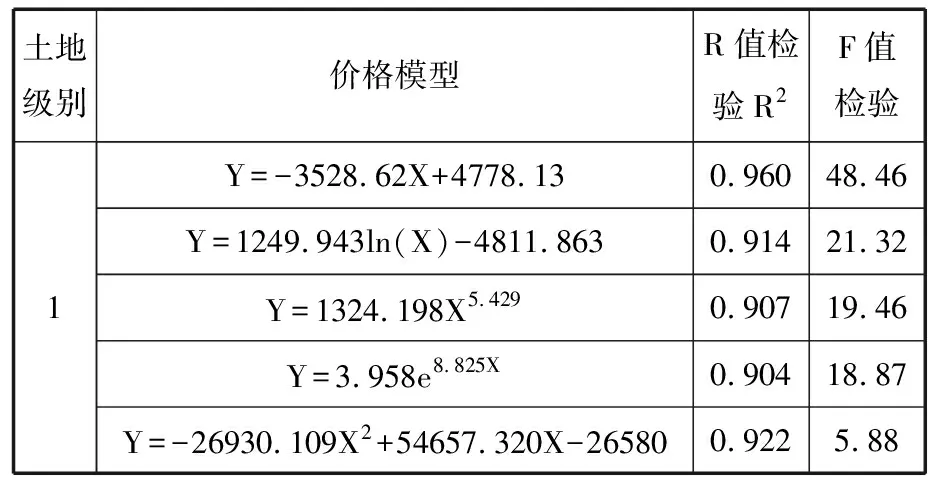
表4 不同级别样点基准地价回归模型

4.回归模型检验

通过以上分析，确定第1级别商服用地基准地价计算公式为：Y=-3528.62X+4778.13，计算得1级商服用地的平均基准地价为：993.22元/m2。

四、灰色模型与回归模型比较分析

(一)运算过程对数据利用比较分析

在基准地价计算过程中，均运用两种模型对所获得数据进行了较为精细的数学分析和相应的数学检验。但两种模型在数据的处理与利用方面还存在一定差异。

回归模型利用不同样点的3年纯收益平均值，通过收益还原法进行计算样点地价。基准地价受到各样点的不同年份的数据影响。而在计算过程中，影响很难消除或降低，从而影响所计算基准地价的准确性。

灰色模型预测4个年份不同样点纯收益平均值，从而清晰反映各年份收益情况，预测值与各年份实际值相接近。如果平均纯收益预测值变化平稳而有规律，则说明降低了不同年份政策和经济等因素所导致的纯收益非正常变化对于商服用地基准地价的影响。

(二)计算结果比较分析

时效性是基准地价基本属性之一，其反映估价时点下的区域土地在开发程度、权利状况、市场供求等因素影响下的平均价格水平。由于基准地价还具有时效性，一般城镇基准地价时效为2到3年，因此将3种模型所求得的计算结果与区域土地出让价格进行比较(见表5)。

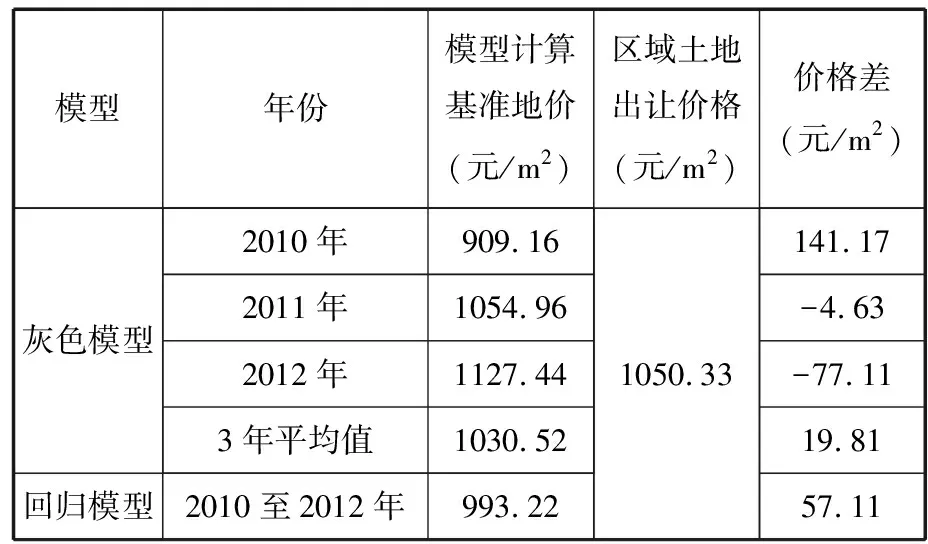
表5 基准地价对比分析

由表5可以看出，灰色模型计算得到的基准地价表现为总体上升趋势；用所求得3年基准地价平均值与区域内类似土地出让价格相比较，灰色模型的价格差小于回归模型计算得到的平均基准地价差。

(三)模型应用比较分析

回归模型是建立在划分定级单元地价总分值基础上的相关函数。因此，划分定级单元地价总分值决定着模型的结果即地价。定级单元的划分受到定级因素、因子的选择和权重的确定影响；测算样点地价的关键点是商服用地纯收益值，国家地区政策、法规、经济环境的变化，均会对样点地块纯收益的值产生影响，以上因素均会影响回归模型计算基准地价的准确性。

灰色模型不需选择因素、指标、因子和确定权重，避免在计算过程中产生误差。在预测预期纯收益时，不用考虑大量历史数据以及数据典型分布情况。对已掌握的信息进行一定合理的技术处理，根据处理后的信息数据建立模型。从更高的层次对系统动态过程进行描述，科学性和预测精度均较高，很大程度上降低了政策、法规、经济环境的影响，能够比较真实地反映商服用地收益的实际情况和发展趋势。

五、结 论

通过上述两种模型在计算过程、计算结果和模型应用方面的比较与分析，可知灰色模型计算得到的基准地价3年平均值与区域类似土地出让价格更加接近，同时清晰地反映出未来一定年份价格变化的趋势，从而可以为更新基准地价提供依据。

另外，灰色模型虽然能够在一定程度上提高价格估算精度，但是仅仅利用其预测所得的纯收益值，用单一收益还原法来计算基准地价，无法准确体现基准地价更多的经济属性。而两种模型结合计算基准地价，以划分定级单元地价总分值为基础，可在提高基准地价的准确性的同时兼顾区位因素等经济属性，体现出基准地价应具有的时空性的特征，从而对农用地级别基准地价进行更加准确的计算，将成为进一步研究的方向之一。

作者文献：

[1]王秋龙.河北省深州市农用地基准地价评估方法比较研究[D].河北师范大学硕士学位论文，2007.

[2]沈 晶，吴 群.我国基准地价评估方法研究[J]. 资源与产业，2007，9(1)：74-76.

[3]董 洁，王占岐.基于基准地价更新成果的地价内部结构比率变动分析[J]. 湖北农业科学，2013，52(14)：3456-3464.

[4]刘耀林，焦利民.人工神经网络的基准地价评估方法研究[J].地球信息科学，2002，(4)：1-6.

[5]王 伟，漆 炜.顾及地价空间分布规律的城市基准地价以价定级方法研究[J]. 武汉大学学报(信息科学版)，2011，36(6)：747-751.

[6]易嗣鑫.基于K-均值聚类法城镇土地定级和基准地价更新研究[D].湖南农业大学硕士学位论文，2012.

[7]陈 丹，兰泽英.基于城市引力场模型的城镇土地基准地价平衡探讨[J]. 测绘科学，2013，38(1)：63-67.

[8]王海军，张德礼.多因素综合评价法划分征地区片方法研究[J].华中师范大学学报(自然科学版)，2006，40(4)：614-616.

[9]张利萍，郑彦玲，郑玉建.基于灰色系统理论的新疆综合地价预测及影响因素分析[J]. 数学的实践与认识，2013，43(2)：81-89.