庙沟铁矿崩矿步距与进路间距的耦合优化研究
高 锋,甘德清,陈 超,卢宏建,李泽营
(1.河北联合大学矿业工程学院,河北 唐山 063009;2.河北钢铁集团矿业有限公司庙沟铁矿,河北 秦皇岛 066000)
无底柱分段崩落法是安全高效的采矿方法,基本特点之一是覆岩下放矿[1]。结构参数和放矿参数选择不当,将增大矿石损失贫化,造成技术经济指标恶化[2]。矿石损失浪费了矿山的基建投资,降低了矿山产量和矿山服务寿命,导致矿产资源的永久丢失。矿石的贫化降低采出矿石的品位,增加了回采、运输和提升等费用,加大破碎和选别的负荷,精矿品位低,尾矿产出率大且有用成分含量高,增加尾矿库安全管理和矿区环境治理的困难[3]。国内外学者结合工业试验,室内物理放矿试验和数值模拟的方法,进行了大量放矿研究,基于椭球体放矿理论体系,提出了许多新型放矿理论和经验公式[3-6]。以河北钢铁集团庙沟铁矿露天转地下开采为工程背景,结合放出体与崩落体最大程度吻合的原则,联合应用数值计算和室内试验的方法,耦合优化庙沟铁矿崩矿步距和进路间距。
1 矿山简介
庙沟铁矿是河北钢铁集团的主采矿山之一,目前生产规模245万t/a,露天境界内资源储量1721.79万t,露天开采还可以维持8.5年,亟需转入地下开采。地下开采矿石储量4960.2万t,设计年产量为300万t,无底柱分段崩落法开采。矿体埋深500m,主矿体平均厚度为16.3~26.3m,最大厚度72.41m,倾角70~85°,全长近1400m;其余矿体平均厚度3.5~7.7m,倾角75~87°。矿区内围岩、矿石硬度系数为10~14,稳固性好,坑内正常涌水量9283.6m3/d。地下开采设计利用的资源储量平均品位TFe29.30%,mFe24.27%。
矿山引进SimbaH1354采矿钻机5台,最大钻孔深度达51m,Toro1400电动铲运机4台,额定斗容5.4m3。综合考虑矿石围岩稳固性、矿体赋存状态和矿山技术装备的工作性能,设计采用20m分段高度,断面尺寸为4m×4.5m的采矿进路。
影响无底柱分段崩落法放矿效率的因素很多,如采场结构参数、崩落矿石块度、崩矿步距、矿岩物理力学性质等。由于爆破技术的进步,矿石块度可以通过爆破技术得到较好的控制。分段高度、出矿口断面和出矿设备确定以后,影响矿石回收效率的主要因素为进路间距和崩矿步距。进路间距和崩矿步距在对放矿效率的影响中彼此关联,有必要进行耦合优化。
2 放矿理论计算
2.1 结构参数计算模型
无底柱分段崩落法端部放矿时,可以近似认为放出体是下部放出口截切的半个旋转椭球体[3],分段高度hf和放出体高度h的近似关系见式(1)。
h=2hf-hc
(1)
矿石实际体积回收率是崩矿步距r的函数[7],无底柱分段崩落法崩矿为挤压爆破,崩矿步距和垂直进路方向的椭球体短半轴b的简化计算见式(2)。
r=0.6b
(2)
根据崩落体和放出体相吻合的原则,沿进路方向的椭球体短半轴c的简化计算见式(3)。
(3)
由沿进路方向短半轴b,放出体高度和放矿口宽度可以计算放出椭球体的体积、偏心率ε和进路间距S的近似值[3],见式(4)。
(4)
S≈2b+W
(5)
(6)
式中:W为进路宽度,m;hc为进路高度,m;n为矿石松散系数,1~1.5。其中,放矿高度h近似等于放出体的长轴2a。
2.2 回贫差计算模型推导
由于放矿时矿石和岩石与矿壁之间的摩擦作用,半无限边界(端部)条件下出矿的放出椭球体长轴和矿壁之间成一个夹角,放出体为前倾扁椭球缺[3]。利用前倾扁椭球体缺几何模型,借鉴前人的研究成果[2-7],推导无底柱无底柱分段崩矿法放矿质量回贫差计算模型。
椭球体放矿实际体积贫化率和实际体积回收率计算见式(7)、式(8)。
(7)
(8)
式中:c为沿进路方向的短半轴;Aac为a2tan2θ+c2;θ为流轴与端壁夹角;L1为atanθ,θ为放出体长轴与矿壁之间的夹角,一般为2~4°;N为漏斗母线在垂直进路方向上所截线段的长度,N=b+(hf+1-a)tanφ;Aab=a2tan2φ+b2,φ为矿岩平均流动角的余角,在实验室条件下为15~20°。
在无底柱分段崩落法放矿研究中,使用质量回贫差便于研究结果的对比分析。引入矿石密度与废石密度之比α,物理相似模拟试验覆盖层岩石品位一般为0,推导出实际体积贫化率pv与实际质量贫化率pm、实际体积回收率ηv与实际质量回收率ηm之间的转换关系式,从而推导出质量回贫差的计算公式。如覆盖岩石不含品位,体积贫化率为放出岩石体积与放出矿岩体积之和的比,近似等于实际体积贫化率,见式(9)。
(9)
(10)
(11)
(12)
无底柱分段崩落法的回采进路菱形布置,放出椭球体体积等于放出矿石与岩石体积之和,单步距回采的实际体积回收率具有等效公式(13)。
(13)
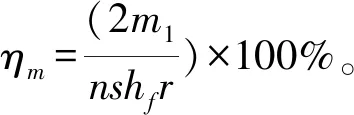
(14)
(15)
(16)
式中:m1,V1为单步距放出矿石的质量和体积;m2,V2为单步距放出岩石的质量和体积,无贫化放矿时为0。
2.3 计算结果
以20m分段高度、4.5m进路宽度和4m进路高度为初始参数,利用以上数学模型,首先进行崩矿步距为2.8m、3.2m、3.6m、4.0m、4.4m的耦合计算,根据计算结果进行加密计算,得到不同步距条件下的进路间距和质量回贫差。计算结果见表1。
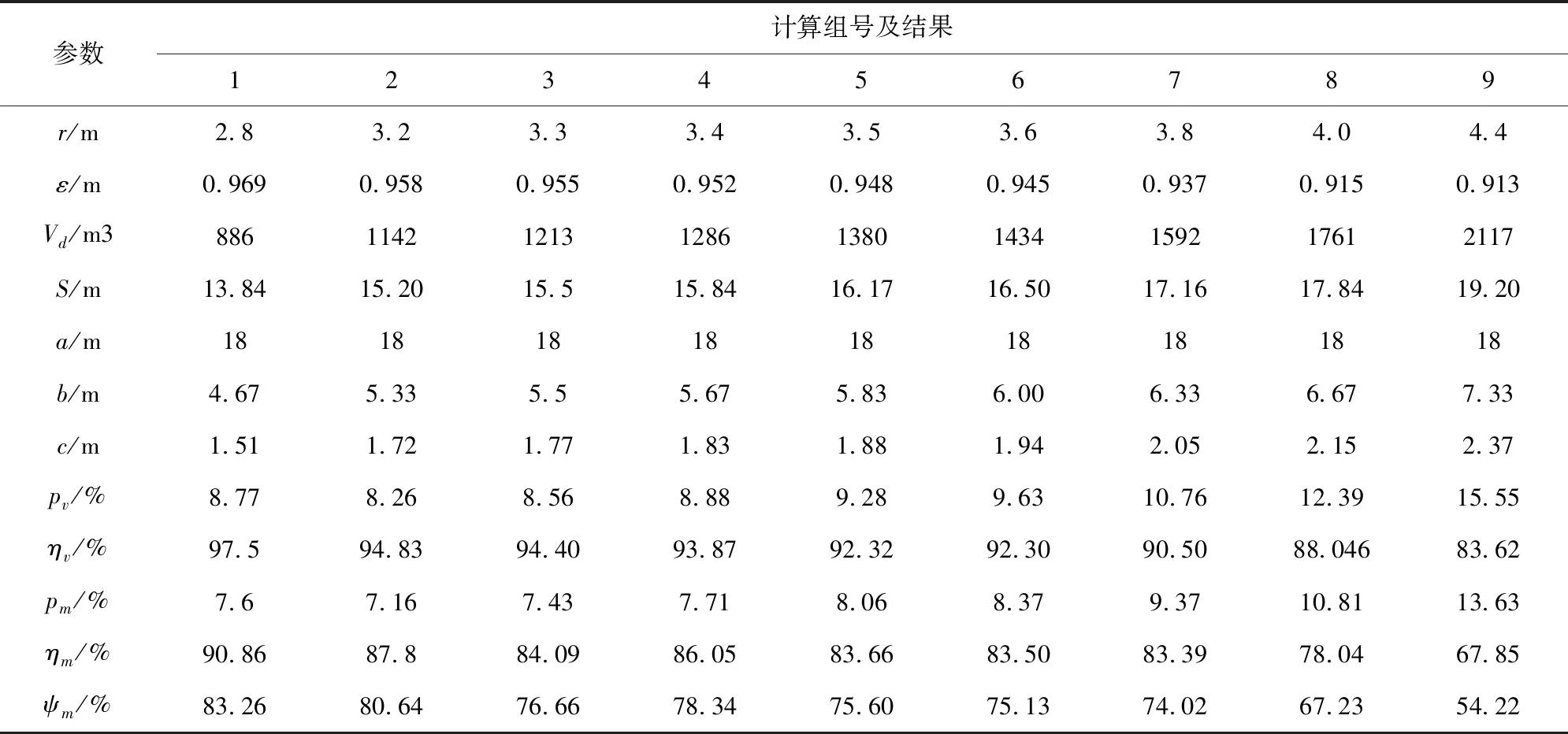
表1 无底柱分段崩落法放矿参数计算结果
3 单进路放矿试验
固定分段高度20m不变,改变进路间距和崩矿步距。考虑到室内试验条件,结合理论计算结果,参考类似矿山无底柱分段崩落法放矿研究与应用情况[8-11],试验参数组合为20m×15m×3.2m,20m×16m×3.4m,20m×16.5m×3.6m,20m×17m×3.8m,20m×18m×4.0m,20m×19m×4.4m。
制作1∶50比例尺立体放矿模型,用磁铁矿和白云岩作为试验材料,根据设计的爆破块度和覆盖层粒级组成按1∶50的比例进行破碎,测出破碎后的矿石和岩石的粒级组成如表2所示。矿石松散体重2.105t/m3,湿度0.8%。岩石松散体重1.798t/m3,湿度0.6%。
为提高试验过程中椭球体发育的相似性,采用栅式嫁接矿壁,使下落的矿石和岩石与矿壁真实接触摩擦,使用1∶50铰接式活动铲斗,模拟铲运机动作,按一定顺序均匀出矿。

表2 矿石和岩石粒级组成
实时记录铲出的矿石和岩石质量,计算矿岩体积,按1∶50比例进行换算成实际体积。当放出矿岩实际总体积达到表1中与崩矿步距对应的放出体体积时,停止出矿,计算矿石质量贫化率,结合进路中单步距承担的矿石量,计算矿石质量回收率。试验结果如表3所示。
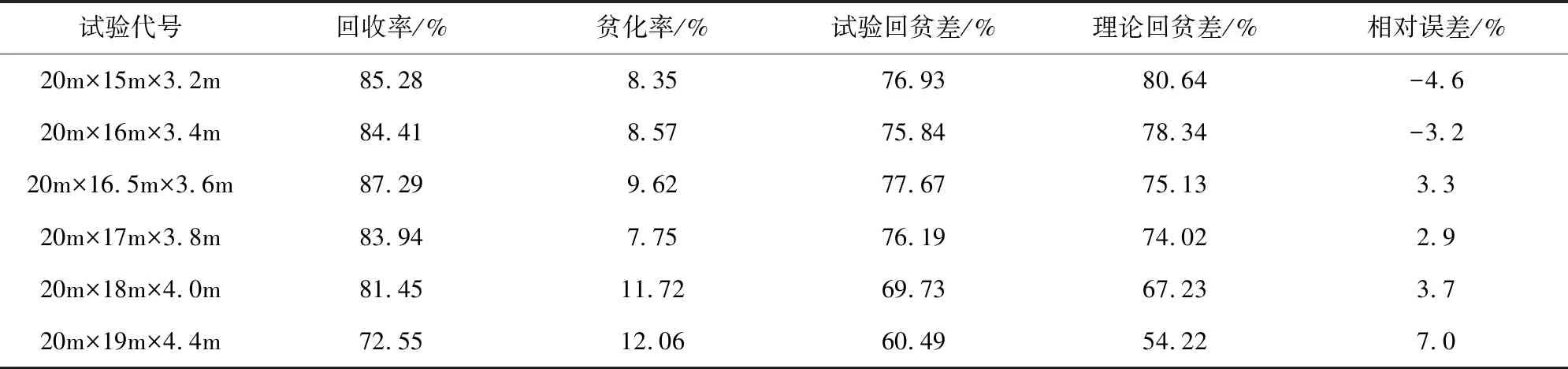
表3 立体放矿试验结果及其与理论回贫差的误差数据
立体相似模拟试验得出,理论计算回贫差与放矿试验回贫差的绝对误差在±10%以内,证实了质量回贫差公式推导的正确性和理论计算的可靠性;6组相似模拟验中,16.5m进路间距、3.6m放矿步距放矿的矿石回贫差最高。
4 总结
以放出体和崩落体最大程度吻合理论为基础,基于实际体积贫化率和实际体积回收率推导质量回贫差的计算模型,为无底柱分段崩落法放矿研究结果的对比分析提供直观便捷的途径。通过多组1∶50比例尺立体相似模拟放矿试验,验证质量回贫差计算模型和理论计算结果是可靠的。结合数值计算结果,进行立体相似模拟放矿试验,试验的相似性和可靠性高。根据研究结果,推荐矿山使用16.5~17m进路间距和3.6m 的崩矿步距进行工业实验。
[1] 解世俊.金属矿床地下开采[M].北京:冶金工业出版社,1989.
[2] 刘兴国.放矿理论基础[M].北京:冶金工业出版社,1995.
[3] 熊国华,赵怀遥.无底柱分段崩落采矿法[M].北京:冶金工业出版社,1989.
[4] 刘兴国,张国联.论无底柱分段崩落法放矿方式[J].金属矿山,2004(02):5-7,10.
[5] 余健.高分段大间距无底柱分段崩落采矿贫化损失预测与结构参数优化研究[D].长沙:中南大学,2008.
[6] 任凤玉.随机介质放矿理论及其应用[M].北京:冶金工业出版社,1994.
[7] 安龙,徐帅,李元辉,等.基于多方法联合的崩落法崩矿步距优化[J].岩石力学与工程学报,2013(04):754-759.
[8] 连民杰,李占科.北洺河铁矿无底柱分段崩落法大结构参数确定[J].金属矿山,2004(02):14-16,23.
[9] 涂文知,马建军,王文中.无底柱分段崩落法过渡分段放矿方式优化研究[J].金属矿山,2007(09):32-34.
[10] 吕向东,杨作华.镜铁山矿无底柱分段崩落法放矿方法的实践[J].金属矿山,2010(02):46-50,54.
[11] 范庆霞.梅山铁矿采场崩矿步距的探讨[J].金属矿山,2007(09):24-27.

