基于余弦距离的人体运动数据行为分割算法
邢薇薇,仝磊鸣,张毅,任程
(1.北京交通大学 软件学院,北京,100044;2. 北京交通大学 计算机与信息技术学院,北京,100044;3. 煤炭科学研究总院,北京,100013)
近年来,在计算机图形学领域中,随着运动捕捉技术的发展[1],人体运动数据日益庞大,如何有效利用这些数据已变得非常重要。其中,对运动捕捉数据的行为进行分割成为运动数据分析与合成的一个不可或缺的重要处理过程。它的主要目的是将包含有不同运动类型的长序列分割成单一的运动,形成具有单一运动类型等语义描述信息的运动片段,以便于在人体运动数据库中的组织和存储管理,为人体运动数据的有效分析以及人体动画运动合成的数据重用等创造条件。本文提出一种新的无监督的人体运动捕捉数据的自动行为分割算法,并采用一组骨骼夹角直方图表示人体运动序列的姿态特征。骨骼夹角[2]反映了人体运动骨骼的生理特征。对于一段运动数据序列,首先选取最能刻画人体运动姿态的主要骨骼夹角作为关键角;然后,对每个关键骨骼夹角数值随序列变化的情况进行直方图统计,并建立所有关键角的直方图统计特征向量作为人体运动序列的描述特征。对于一段包含多种运动类型的人体运动序列,定义滑动比较窗口,随着比较窗口在序列上从起点向终点滑动,计算当前位置比较窗口中前半段与后半段2 部分运动序列的骨骼夹角直方图特征的余弦相似度,从而获得该序列的余弦相似度数值曲线。比较窗口中前、后2 半部分的人体运动姿态特征越相似,对应的余弦相似度越接近于1,所以,运动序列中2 个不同运动类型切换处的余弦相似度曲线会出现1 个低谷,余弦相似度曲线上的区域最小值处对应着不同类型运动行为的分割点。为了避免余弦相似度曲线上的噪声及数值波动等对人体运动行为分割点判断的影响,本文使用曲线简化算法对余弦相似度曲线进行近似表示,从而检测出2 段不同类型运动行为的切分点,实现对运动数据的有效分割。
1 相关工作
随着运动捕捉技术的发展,人体运动捕捉数据日益庞大。为了有效地利用这些运动数据,使用者常常需要将长序列的高维人体运动数据按照人体运动类型的语义描述进行有效分割,划分为具有单一运动类型的数据片段,以便于后续对人体运动捕捉数据进行分析、合成、组织和管理等处理和应用。人体运动行为的分割提取实现对原始的人体运动捕捉数据进行精确的行为分割,以此作为人体运动数据的结构化分析与合成等数据处理的基础,已成为国内外研究人员关注的研究热点。许多研究人员为此进行了大量研究工作,并取得了一系列研究成果。早期的一些研究者以直观的低层运动特征为基础分割运动数据。例如,Pomplun等[3]提出了基于关节空间(joint-space)的运动分割算法。Fod 等[4]通过检测人体关节运动角速度过零点的方法分割人体运动数据。
针对原始人体运动捕捉数据维数高、处理计算量大的难题,一些研究者提出基于数据降维的分割方法。Barbic 等[5]认为不同的人体运动行为可以用不同的本征维数来表示,通过主成分分析 PCA(principal component analysis)对人体运动数据降维,复杂运动类型的PCA 子空间比单一运动的PCA 子空间有更高的维度,因此,最后在子空间中通过投影误差来检测行为分割点的位置。肖俊[6]提出了一种基于非线性流形的三维人体运动数据的行为分割方法,采用非线性流形降维技术ISOMAP(isometric mapping)对人体运动数据进行降维,使用k-均值算法对人体运动聚类,从而可以更精确地得到行为分割点。杨涛等[7]提出了一种基于分层曲线简化的运动捕捉数据提取关键帧的方法。Peng[8]把人体骨架分为上肢和下肢2 部分,利用降维后的中心距离特征来表示三维人体运动,通过使用低通滤波器对人体运动数据进行降噪以得到行为分割点。
另一类分割方法通过设计分类器处理机制,实现对人体运动数据的行为分割。Arikan 等[9]通过构造支持向量机SVM(support vector machine)对人工标注的训练数据集进行人体运动数据的行为分割。Kahol等[10]利用动态层次结构表示人体解剖学特征,使用朴素贝叶斯(naive Bayes)分类器完成人体运动数据的行为分割,但是,这种方法在很大程度上比较依赖于训练数据集和经验值。杨跃东等[11]提出了一种基于“运动串”的运动分割方法,运动数据经过谱聚类、时序回复和最大值滤波后生成 “运动串”,在人体运动捕捉数据的基础上,对这些“运动串”进行分析和分类,从而实现运动数据的行为分割。Zhou 等[12]采用对齐聚类分析ACA(aligned cluster analysis)方法完成人体运动数据的行为分割,这种方法通过引入动态时间对齐核的概念,度量不同长度的运动序列片段的相似性,采用核k-均值完成人体运动的分类,从而达到行为分割的目的。
另外,一些研究者提出了基于模型的人体运动数据分割方法。Barbic 等[5]在基于PCA 行为分割的基础上提出了基于PPCA 的行为分割方法,认为不同运动类型的数据具有不同的高斯分布,可以根据它们之间的马氏距离来确定行为分割点。此外,他们还使用高斯混合模型GMM(Gaussian mixture model)对不同运动类型的序列进行聚类,当连续帧属于不同GMM 模型时,就确定其为行为分割点。Wang 等[13]使用隐马尔可夫模型HMM(idden Markov model)对运动进行聚类,能够把自然活动序列分割成运动原子片段。Wang等[14]通过使用核动态纹理对周期对称的人体运动数据进行分割以获取它们的运动原子片段。Lu 等[15]提出了基于双阈值多维分割算法,可以将比较复杂的人体运动数据分解成一个简单的动态线性模型序列,从而得到分割点。
在三维人体运动数据处理中,国内外学者提出多种不同的三维人体运动特征表示方法。传统方法通常采用原始运动序列姿态的关节点位置、关节角度、角速度、角加速度等表示。Lee 等[16]提出了一种2 层的结构运动特征的表示方法,其低层把一段序列看成简单的一阶Markov 过程,刻画运动细节,高层通过统计模型对运动数据库进行聚类分析。Muller 等[17]提出关系特征表示方法,使用一组布尔数值定性地描述人体运动序列中人体骨架动力学链特定点之间以及相关身体部件之间的空间几何关系特征。肖俊等[2]采用人体各主要骨骼夹角作为对原始运动数据的几何特征表示,选择人体骨架中四肢部分的8 段主要骨骼作为特征表示对象,提取这8 段骨骼与由Root 关节和Chest关节组成的中心骨骼之间的夹角作为运动几何特征。由于人体骨架四肢部分在人体运动中变化最明显,且在运动描述上更具逻辑性,骨骼夹角既能表示三维人体姿态特征,充分反映人体运动类型变化,又能极大地降低原始三维人体运动数据的维度,为此,本文在采用骨骼夹角作为三维人体运动特征数值表示的基础上,提出使用骨骼夹角直方图统计特征,进行人体运动数据的行为分割。另外,考虑到直方图统计描述中会丢失原有人体运动序列的部分时序特征,例如,一段跑和一段跳的骨骼夹角直方图可能会相似,但在前者中双手和双脚始终保持一前一后,而在后者中双手与双脚的运动方向是一致的,因此,在原有8 段骨骼夹角基础上,增加了左、右上臂间的骨骼夹角和左、右大腿间的骨骼夹角。
本文采用余弦距离度量2 条人体运动数据片段特征的相似性。余弦距离作为一种数据相似性度量机制,通过测量2 个向量内积空间的夹角的余弦来度量它们之间的相似性,可用于任何维度的向量比较,尤其在高维正空间中。余弦距离广泛应用于信息检索和文本处理等方面[18-20],其中,文本通常被建模为词频向量(term–frequency vector)。由于特定文本中所包含词汇往往只占所有词汇集的一部分,词频向量通常为一个高维稀疏向量,因此,计算词频向量相似度时,需要忽略不匹配的词汇,只对2 个文档中都出现的词汇频率进行比较,而使用2 个词频向量之间夹角的余弦进行度量显然比传统欧式距离等度量方法更精确。本文采用骨骼夹角直方图作为人体运动序列统计特征,同样具有高维稀疏向量的特点,使用余弦距离度量2 个特征向量在高维空间分布上的方向差异,相对于比较2 个向量幅值等属性更加直观,且物理意义明显,因此,本文提出基于余弦距离的人体运动序列数据统计特征向量的相似性度量机制。
2 特征提取及运动相似性度量
2.1 骨骼夹角运动特征提取
原始的运动捕获数据是由一系列姿态帧组成的运动序列,每一帧定义了1个层次骨架模型。根关节(root)具有6 个自由度,其中3 个用于表示人体骨架在世界坐标系中的位置,另外3 个定义骨架在世界坐标系中的朝向。对于其余关节,具有3 个自由度,表示它们相对于各自父关节的旋转角度。图1 所示为本文使用的人体骨架模型。
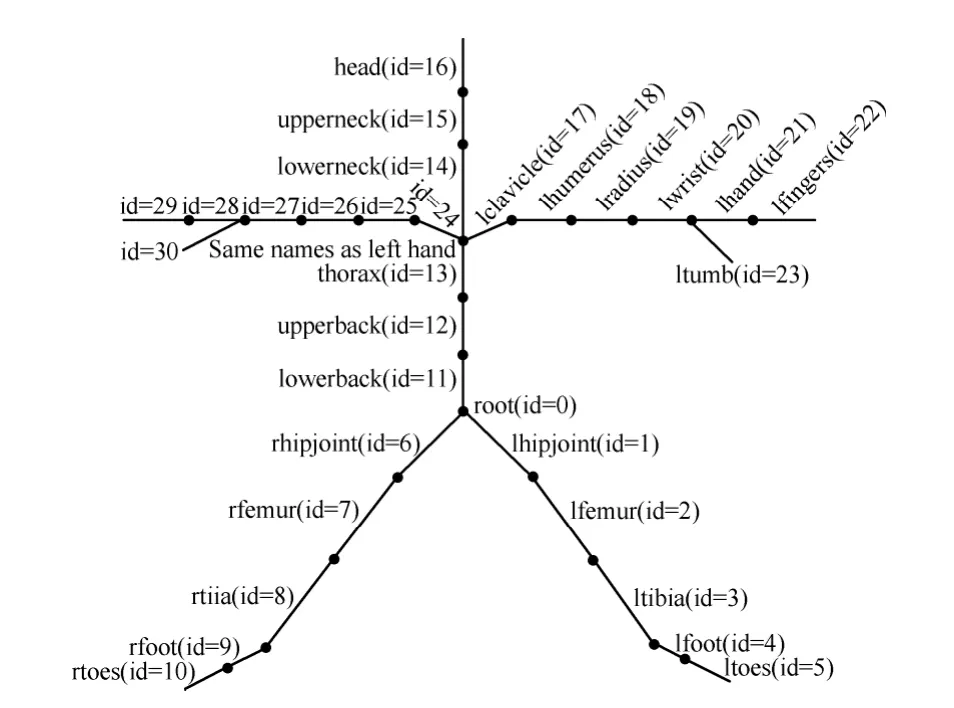
图1 本文使用的人体骨架模型Fig.1 Human skeleton model used in this paper
由于运动类型并不会随着人体位置和朝向的不同而发生变化,因此,本文不考虑根关节的作用。在通常情况下,人体四肢和腰部的变化最显著,基本决定了人体的运动类型;头、手和脚这3 个部位的变化没有规律,对运动的比较会造成很大影响,而它们对于整体运动类型的区分能力非常小。为此,本文采用根骨骼(Broot)与四肢部分的8 段骨骼(Bi, i=1,…,8)之间的骨骼夹角[2]作为描述每一个姿态的运动特征,如表1所示,表中关节点的位置表示,如root,lowerback 和l-clavicle 等符号与图1 中的各关节点的符号一一对应,且B1表示由父关节位置l-clavicle(id=17)指向子关节位置l-humerus(id=18)的骨骼向量,表中其他骨骼向量具有同样的表示含义。

表1 骨骼的向量表示Table 1 Bones definition as vectors pointing from parent joint position to the child
此外,在一段走运动和跳跃运动中,胳膊和腿与根骨骼构成的夹角的分布不会有太大区别。但走路时胳膊和腿是一前一后,而跳跃时,胳膊和腿是同时前伸。基于上述观察,为了进一步提高运动类别的描述和区分能力,本文又增加了2 个骨骼夹角,即左、右上臂骨骼B1和B3之间的夹角以及左、右大腿骨骼B5和B7之间的夹角,与表1 中的8 个骨骼夹角共同作为描述运动姿态的特征。
这些骨骼夹角不仅能够直观地反映人体运动的物理意义,而且能够降低原始高维运动数据的维度[7]。根骨骼Broot和第i 段骨骼Bi之间的夹角θi通过式(1)计算得到:
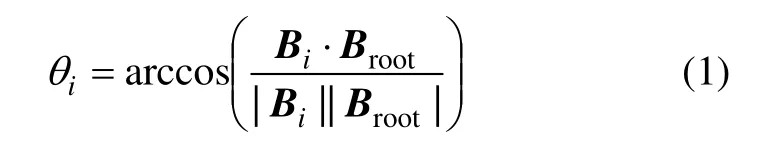
此外,在一段走运动和跳跃运动中,胳膊和腿与根骨骼构成的夹角的分布不会有太大区别。但走路时胳膊和腿是一前一后,而跳跃时,胳膊和腿是同时前伸。基于上述观察,为了进一步提高运动类别的描述和区分能力,又增加了2 个骨骼夹角,即左、右上臂骨骼B1和B3之间的夹角θ9,左、右大腿骨骼B5和B7之间的夹角θ10,与表1 中的8 个骨骼夹角共同作为描述运动姿态的特征。
2.2 骨骼夹角直方图和运动相似性度量
本文采用直方图来描述运动序列中10 个骨骼夹角的分布,并将2 个运动序列的骨骼夹角直方图之间的距离作为运动序列的相似性度量,这是本文分割算法的基础。对于不同类型的运动,其骨骼夹角的变化范围是不同的,但骨骼之间的夹角总是在0 到π 之间,因此,每个骨骼夹角的下限为0,上限为π。
对于给定的1 条运动序列M,为了计算骨骼夹角的直方图,本文将[0,π]平均划分为L 个区间,采用如下计算公式[21]确定L:

其中:N 为运动序列M 所包含的帧数。相应地,在[0,π]上形成了l+1 个边界,这些边界可以表示为

由这些边界构成的区间定义为
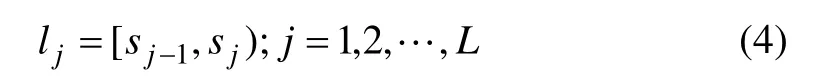
第i 个骨骼夹角的直方图计算公式为
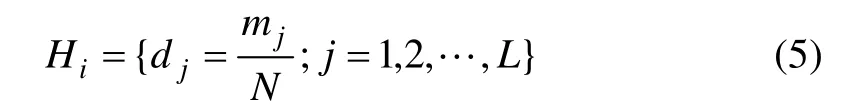
其中:mj为运动序列M 中第j 个骨骼夹角θi落在区间ψj内的频数;j=1,2,…,10,对应于本文选取的10个骨骼夹角。运动序列M 中的每个骨骼夹角的直方图Hi是一个1×L 的向量,将M 的10 个骨骼夹角的直方图向量首尾相连,构成1 个新的1×10L 的向量YM,作为描述运动序列M 的特征向量。
在通常情况下,一类运动中人体骨骼夹角的活动范围并不是都能够占据[0,π]的整个角度空间,于是,[0,π]的L 个区间中有些区间对应的元素为0,表示运动中骨骼不可达的范围空间。可见,骨骼夹角直方图特征是一个高维稀疏向量,本文采用余弦距离来度量2 个高维特征向量之间的相似性,具体通过计算2 个向量之间夹角的余弦来实现。
对于任意给定的2 条运动序列M1和M2,分别提取出对应的特征向量YM1和YM2,则序列M1和M2之间的余弦距离计算公式如下:
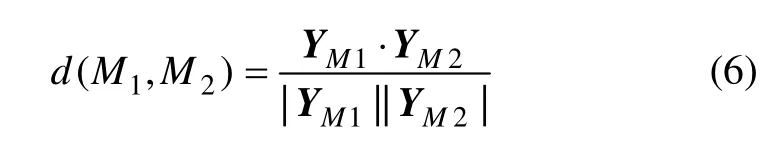
运动序列M1和M2越相似,则对应的特征向量之间的夹角越小,Dis(M1,M2)也越接近于1。
基于骨骼夹角直方图的运动特征不但对原始运动数据进行降维,而且避免了逻辑上相似的运动由于时空变化而导致的数值上的差异[22]。此外,在进行相似性度量计算时,本文的骨骼夹角直方图运动特征不需要像基于DTW(dynamic time warping)的运动相似性度量方法[16,23]一样需要进行预先时间对齐处理。
3 运动分割
3.1 相似度曲线计算
在计算得到运动序列特征和相似性度量值后,需要计算出1 条运动序列的相似度曲线。对于给定的一段运动序列M,首先在M 上定义1 个滑动窗口W,窗口大小为S,窗口每次滑动步长可以根据不同情况进行自定义,本文将窗口步长设置为1 帧。初始窗口的左边缘与运动序列M 的第1 帧对齐,最后1 个窗口的右边缘与运动序列M 的最后1 帧对齐。本文的滑动窗口定义为
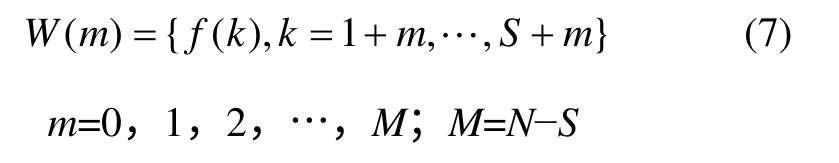
其中:m 为当前窗口的序号;f(k)为该窗口包含的运动序列M 中的第k 帧。对于滑动过程中的每一个窗口W(m),提取出前半个窗口对应的运动片段的特征向量Yfirst-half和后半个窗口对应的运动片段的特征向量Ysecond-half,然后,根据余弦距离计算该窗口内前、后2部分运动片段的相似度,如下式所示:
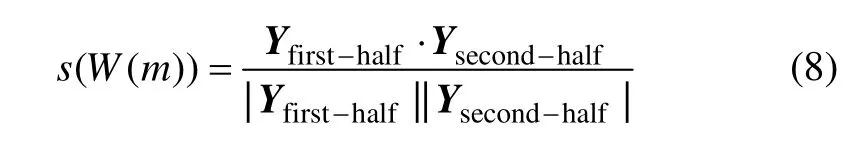
于是,根据s(W(m))得到1 条相似度曲线,该曲线起始于运动序列M 的第S/2 帧,终止于第N-S/2 帧。
若M 只包含1 种运动类型,则每个窗口中前后2段运动应该属于同一个运动类。根据式(8),s(W(m))将接近于1,得到的相似度曲线是1 条接近于1 的水平线。若M 是1 条由2 类运动前、后相连构成的运动序列,则当滑动窗口在第1 类运动上滑动时,相似度保持相对恒定。当第2 类运动进入滑动窗口时,首先进入的是滑动窗口的后半部分,此时,窗口的前、后2 段运动的相似度将逐渐减小。当第2 类运动完全占据滑动窗口的后半部分时,窗口的前、后2 段运动为2 类不同的运动,因此,计算的相似度将降到最小。随着滑动窗口继续向后移动,第2 类运动开始进入窗口的前半部分,此时,窗口的前、后2 段运动之间的相似度逐渐开始增大。当滑动窗口完全进入第2 类运动时,相似度达到最大,如图2 所示。图2 中,运动序列M 包含2 类运动行为,每类运动包含大约500 帧,滑动窗口的大小L 设置为100。从图2 可以看出:运动序列中2 类运动行为的分割点为曲线的极小值点。
滑动窗口长度的选择应满足如下2 个条件:

图2 包含2 类运动行为的运动序列M 的相似度曲线Fig.2 Similarity plot motion sequence M including two behavior sequences
(1) 滑动窗口应具有足够长度,至少应容纳运动序列M 中最大周期运动的2 个周期,以包含充分的运动序列帧数据并能够反映该类行为的运动特征信息,只有这样,窗口的前、后2 半部分才能获取足够的数据来建立有效的骨骼夹角直方图。
(2) 滑动窗口的一半应小于运动序列中所包含的全部运动类中最短语义运动片段的长度。如图3 所示,灰色和黄色片段分别表示2 类运动序列,其中,深色运动序列小于窗口的一半。当滑动窗口中心点从A 点滑动到B 点时,深色运动逐渐进入窗口,窗口前、后2 半部分之间的相似度逐渐减小;当滑动窗口从B 移至C 点时,由于后半窗口中的2 类运动占据比例保持不变,此时,相似度也保持恒定;由C 点滑至D 点时,相似度开始增加。从图3 可以看到:C 点是行为分割点,而在这种情况下,B 点也很容易被选择为分割点,于是产生分割错误。因此,在设置滑动窗口长度时,其尺寸的一半应小于运动序列中的最短运动类型运动片段。
因此,需要根据行为类型的运动周期及最短的运动类型片段长度,设定适当的滑动窗口长度。
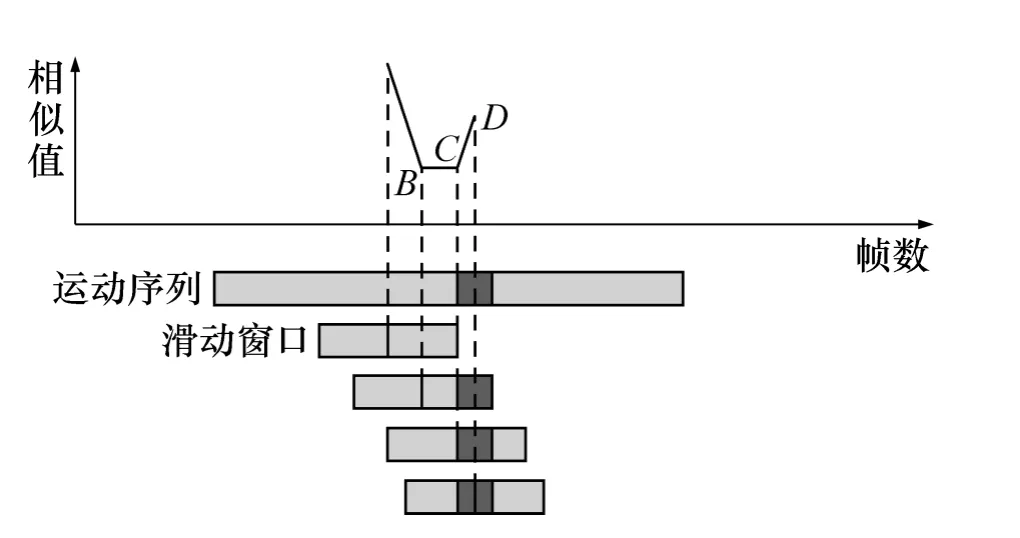
图3 窗口一半大于运动序列中待分割出的最短语义运动片段时的错误分割Fig.3 Error case of segmentation when half of window size is larger than the shortest behavior clip in the motion sequence
3.2 分割点检测
给定一条运动序列,能够计算得到1 条对应的相似度曲线。经过上述分析得知,相似度曲线的极小值即为不同运动类型的分割点,本文的目标就是找出相似度曲线上的极小值点。为了确定分割点,最直接的作法是通过设置阈值,选择小于该阈值的点作为分割点。然而,由于给定的运动序列中任意2 种类型运动之间的最小相似度并不能预先确定,因此,阈值法并不适合。在一段运动序列中,即使都属于同类型的运动,不同周期的运动姿态也会有差异,这会导致相似度曲线产生波动;此外,滑动窗口长度的选择也会对相似度曲线产生影响。但实际上由上述原因导致的相似度曲线波动的幅度远远小于由运动类型改变引起的波动幅度,因此,本文采用曲线简化算法来忽略相似度曲线中较小的波动变化而保留较大的波动变化,达到分割点检测的目的。
对于得到的相似度曲线(如图4(a)所示),首先用连接该曲线首尾两端点的线段来近似表示该曲线(如图4(b)所示),近似效果可以通过计算曲线到该线段的最大距离来衡量。若该距离大于预先设定的阈值,则将线段2 个端点与曲线到该线段最远距离的点分别相连,并删除该线段(如图4(c)所示)。然后,该过程一直递归直至最大距离小于阈值为止,如图4(d)所示。

图4 曲线简化算法示意Fig.4 Demonstration for curve simplification
曲线简化算法中的阈值为经验值,通过实验进行设置。设置过大会将一些分割点忽略,过小会受到噪声和数据波动的影响,可能会选出一些错误的分割点。图2 中的相似度曲线经过曲线简化处理后得到的近似曲线如图5 中的折线所示。本文通过在包含大多数运动类别的训练样本集上进行的实验来确定曲线简化中的阈值,据此设置阈值为0.08。图5 中小方框是近似曲线的连接点,为了找到分割点,需要从这些连接点中检测出极小值。从图5 可以看出:极小值的点与左边相邻的连接点构成的直线斜率为负,与右边相邻的连接点构成的直线斜率为正。因此,可以根据该方法从这些曲线连接点中快速提取出运动序列的分割点。
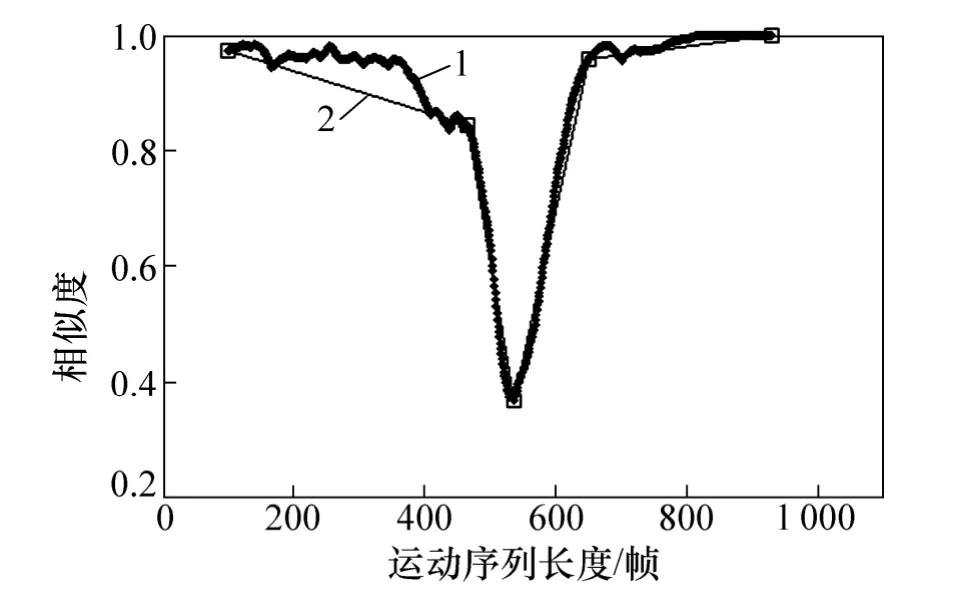
图5 运动序列相似度曲线的简化结果Fig.5 Simplification result for motion sequence similarity curve
4 实验结果及分析
为了进一步说明算法的适用性和有效性,本文设计2 组实验。实验数据选自美国CMU 的人体运动捕捉数据库[24],其运动数据采用AMC 格式[25],数据描述使用欧拉关节角。
4.1 余弦相似性度量的有效性
从CMU 数据库选取7 类不同的运动,包括走(walking)、跑(running)、坐(sitting down)、前跳(forward jumping)、爬(climbing)、伸手臂(arm stretching)、打拳(punching),并从数据库中随机抽取这7 类运动行为的14 段运动序列,每类包含2 段运动序列,每段序列长度为240 帧。2 个相同类型的运动片段之间的余弦相似度理论上应该接近于1。为了验证算法的正确性和有效性,建立14×14 的相似性矩阵,矩阵的每一个元素是其所在行和列对应的2 类运动序列的余弦相似度,如表2 所示。
事实上,每个运动类与其自身相似,相似度为1,与同类运动的不同序列片段也应该具有很高的相似度。在相似性矩阵表中,用灰色矩形标识出的对角线元素是2 个同类运动相同片段和同类不同片段之间的余弦相似度。从表2 可以看出:同类运动相同片段的相似度为1,同类运动不同片段之间也具有比其他运动片段更高的相似度,接近于1。例如,run1 和run2之间的相似度为0.97,jump1 和jump2 之间的相似度为0.94。实验结果表明:本文提出的余弦距离度量对人体运动捕捉数据序列片段具有良好的描述能力和区分能力,为实现运动捕捉数据的自动化高效分割创造了有利条件。
4.2 运动序列的自动分割
从CMU 数据库中选取对第86 号实验者采集的14段人体运动捕捉数据序列,每段运动序列大约8 000帧,包含约10 类人体运动,包括走(walking)、跑(running)、打拳(punching)、爬(climbing)等,每类运动行为的周期为50~200 帧。表3 所示为实验用运动序列数据集的详细信息。
为了测试本文方法的分割效果,对运动序列的分割点进行了预先人工划分,将其作为算法自动分割结果的比较标准,并与Barbic 等[5]提出的基于PPCA 的运动分割算法进行比较。部分运动行为的分割实验结果如图6 所示。
从图6 可以看出:在部分运动数据的分割实验中,对于走这类运动行为,基于PPCA 的算法在行走过程中的拐弯处多得到1 个分割点,错误地将同一个走运动行为分成了2类。例如,图6(a)中运动序列86_03.amc的第1 个和最后1 个分割点,图6(b)中运动序列86_05.amc,图6(d)中运动序列86_08.amc,图6(e)中运动序列86_11.amc 和图6(f)中运动序列86_13.amc的第1 个分割点,图6(c)中运动序列86_07.amc 的第8个分割点。
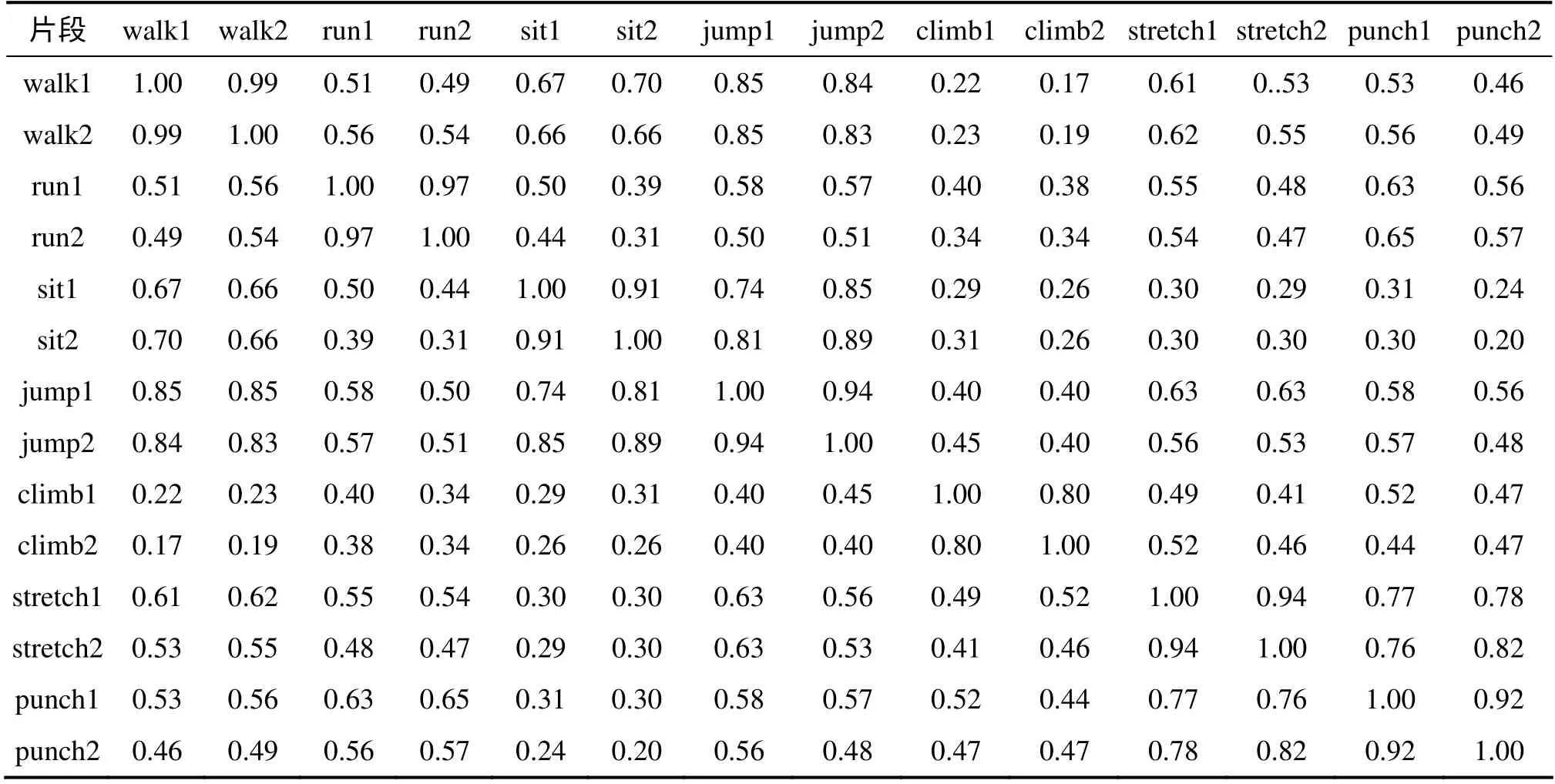
表2 7 类运动14 段序列的相似性Table 2 Similarity of 14 motion sequences belonging to 7 behaviors

图6 运动分割比较实验结果Fig.6 Comparison experimental results between our method and PPCA algorithm for motion segmentation

表3 实验中用于行为分割的人体运动数据序列Table 3 Human motion data sequences of behavior segmentation used in experiments
在图6(b)中,对于86_05.amc 运动序列,手工分出的第4 个分割点是将前跳和右腿单腿跳分开,而PPCA 却漏掉了这个分割点。根据数据库中采集的原始运动数据序列,在手工分出的第9 和第10 个分割点之间是一段“扬起手臂挥打”的动作,PPCA 却将其分为2 段。在图6(e)中,对于86_11.amc 序列手工分割的第2 个分割点是将双臂伸展与右臂单独伸展2 段运动分开,第4 个分割点是将双臂伸展与左臂单独伸展分开。从图6 可以看到:实验中在曲线简化算法阈值设为0.08 的情况下,手工分割中的第2 个和第4 个分割点没有找到,但可以通过调整阈值设置实现不同粒度的运动行为分割。在图6(f)中,对于86_13.amc 序列手工分割的第4 个和第5 个分割点之间是一段静止站立的动作,PPCA 却将它们与前、后两段运动融合在一起而没有分开。手工分割的第6 个和第7 个分割点之间是一段“站在梯子上四处张望”的动作,PPCA却将其分成了3 段。手工分割的第7 个和第8 个分割点之间是一段短暂的“站在梯子上指点”动作,由于该动作与前一个动作很相近,且持续时间很短,因此,这2 种方法都没有将其分割开。
为了进一步说明本文提出的分割算法的性能,计算了运动分割实验结果的准确率(p)和召回率(r)。用Ncorrect表示算法检测出的正确的分割点数目,Treport表示算法检测到的总的分割点数目,Thuman表示手工分割点的数目,则准确率定义为

召回率定义为

对于实验中的14 条运动序列,通过准确率和召回率比较了本文提出的算法与PPCA 算法的分割结果,如表4 所示。

表4 本文COSINE 算法和PPCA 的准确率及召回率Table 4 Precision and recall of our COSINE based method and PPCA algorithm
据准确率可知本文提出的方法较PPCA 方法在实验数据库中能够得到更多正确的分割点,据召回率可知本文算法得到的分割点中有效分割点更多,也说明本算法良好的行为分割性能。
需说明的是:由于相似度曲线是从运动序列的第S/2 帧开始,第N-S/2+1 帧结束,因此,[1,S/2]和[N-S/2+1,N]这2 段范围内的分割点将会检测不到。为了避免该问题,本文在设置窗口长度时,保证窗口长度的一半小于人体最短运动类型的最短运动语义片段长度,这样,在[1,S/2]和[N-S/2+1,N]的范围内,将不存在分割点,从而保证了本文算法的鲁棒性。
5 结论
(1) 针对运动检索与合成等一系列运动数据重用方法对单一语义运动序列的需求,本文提出了一种新的无监督的人体运动捕捉数据运动行为的自动分割算法,将运动序列自动划分为不同类型的行为运动。算法通过计算描述人体运动序列姿态的每个骨骼夹角的统计直方图,提取运动序列的特征向量。在此基础上,本文提出了基于余弦距离的运动序列相似性度量计算方法,并通过定义滑动窗口和曲线简化得到运动序列的分割点。
(2) 采用骨骼夹角直方图作为运动序列的描述特征,不仅对原始运动序列进行了降维,而且在相似性度量方面避免了时空变化所带来的影响,不需要预先进行时间对齐计算。可见,本文的骨骼夹角直方图特征和余弦距离度量大大减小了对运动序列进行比较的计算量,提高了算法的运行效率,实验结果也充分说明了算法在进行运动行为分割上的正确性、有效性和良好性能。
[1] Moeslund T B, Hilton A, Kruger V. A survey of advances in vision-based human motion capture and analysis[J]. Computer Vision and Image Understanding, 2006, 104(2/3): 90-126.
[2] 肖俊, 庄越挺, 吴飞. 三维人体运动特征可视化与交互式运动分割[J]. 软件学报, 2008, 19(8): 1995-2003.XIAO Jun, ZHUANG Yueting, WU Fei. Feature visualization and interactive segmentation of 3D human motion[J]. Journal of Software, 2008, 19(8): 1995-2003.
[3] Pomplun M, Matarić M J. Evaluation metrics and results of human arm movement imitation[C]//Proceedings of International Conference on Humanoid Robotics (Humanoids 2000). Boston,USA: IEEE-RAS, 2000: 7-8.
[4] Fod A, Mataric M, Jenkins O C. Automated derivation of primitives for movement classification[J]. Autonomous Robots,2002, 12(1): 39-54.
[5] Barbic J, Safonova A, Pan J Y, et al. Segmenting motion capture data into distinct behaviors[C]//Proceedings of International Conference on Graphics Interface. Ontario, 2004: 185-194.
[6] 肖俊. 智能人体动画若干关键技术研究[D]. 杭州: 浙江大学计算机科学与技术学院, 2007: 42-50.XIAO Jun. Study on intelligent human animation key techniques[D]. Hangzhou: Zhejiang University. School of Computer Science and Technology, 2007: 42-50.
[7] 杨涛, 肖俊, 吴飞, 等. 基于分层曲线简化的运动捕获数据关键帧提取[J]. 计算机辅助设计与图形学学报, 2006, 18(11):1691-1697.YANG Tao, XIAO Jun, WU Fei, et al. Extraction of keyframe of motion capture data based on layered curve simplification[J].Journal of Computer-Aided Design & Computer Graphics, 2006,18(11): 1691-1697.
[8] Peng S J. Motion segmentation using central distance features and low-pass filter[C]//Proceedings of International Conference on Computational Intelligence and Security. Nanning, China:IEEE, 2010: 223-226.
[9] Arikan O, Forsyth D A, O’Brien J F. Motion synthesis from annotations[J]. ACM Transactions on Graphics, 2003, 22(3):402-408.
[10] Kahol K, Tripathi P, Panchanathan S, et al. Gesture segmentation in complex motion sequences[C]//Proceedings of International Conference on Image Processing(ICIP 2003). Barcelona,Spain:IEEE, 2003: II: 105-108.
[11] 杨跃东, 王莉莉, 郝爱民. 运动串: 一种行为分割的运动捕获数据表示方法[J]. 计算机研究与发展, 2008, 45(3): 527-534.YANG Yuedong, WANG Lili, HAO Aimin. Motion string: A motion capture data representation for behavior segmentation[J].Journal of Computer Research and Development, 2008, 45(3):527-534.
[12] Zhou F, Torre F, Hodgins J K. Aligned cluster analysis for temporal segmentation of human motion[C]//Proceedings of International Conference on Automatic Face & Gesture Recognition. Amsterdam, Netherland: IEEE, 2008: 1-7.
[13] Wang T S, Shum H Y, Xu Y Q, et al. Unsupervised analysis of human gestures[C]//Proceedings of IEEE Pacific Rim Conference on Multimedia. Beijing, China:Springer Berlin Heidelberg, 2001: 174-181.
[14] Wang M, Wang W, Li Y, et al. Motion capture data segmentation using kernel dynamic texture[C]//Proceedings of International Conference on Audio Language and Image Processing. Shanghai,China: IEEE, 2010: 592-596.
[15] Lu C M, Ferrier N J. Repetitive motion analysis: Segmentation and event classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26(2): 258-263.
[16] Lee J, Chai J, Reitsma P S A, et al. Interactive control of avatars animated with human motion data[J]. ACM Transactions on Graphics, 2002, 21(3): 491-500.
[17] Müller M, Roder T, Clausen M. Efficient content-based retrieval of motion capture data[J]. ACM Transactions on Graphics, 2005,24(3): 677-685.
[18] Singhal A. Modern Information Retrieval: A brief overview[J].IEEE Data Engineering Bulletin, 2001, 24(4): 35-43.
[19] Marti A H. TextTiling: Segmenting text into multi-paragraph subtopic passages[J]. Journal of Computational Linguistics, 1997,23(1): 33-64.
[20] Peter D T, Patrick P. From frequency to meanings: vector space models of semantics[J]. Journal of Artificial Intelligence Research, 2010, 37(1): 141-188.
[21] Scott D W. Multivariate Density Estimation: Theory, Practice,and Visualization. New York: John Wiley, 1992: 47-94.
[22] Lucas K, Michael G. Automated extraction and parameterization of motions[J]. ACM Transactions on Graphics, 2004, 23(3):559-568.
[23] Eamonn K, Themistoklis P, Victor B Z, et al. Indexing large human-motion databases[C]//Proceedings of International Conference on Very Large Data Bases. Toronto, Canada:VLDB Endowment, 2004: 780-791.
[24] CMU Graphics Lab. CMU Motion Capture Database [EB/OL].[2003-01-01]. http://mocap.cs.cmu.edu/.
[25] Miiller M, Roder T, Clausen M, et al. Documentation mocap database HDM05[R]. Bonn, Germany: Universität Bonn, 2007,9-20.

