一种含导频GNSS 信号的通道组合捕获检测量的设计与优化

林红磊，唐小妹，刘瀛翔，王飞雪

(国防科技大学 电子科学与工程学院，湖南 长沙，410073)

现代化后的导航信号中大多含有导频通道[1]，如Galileo-E1[2]和GPS-L5[3]等信号。对这类信号的捕获，若不进行导频通道与数据通道的组合，将会损失信号中的一部分能量，使得检测损耗增大。目前已有的导频与数据通道的组合捕获算法主要包括非相干组合、差分组合、相干组合捕获算法[4-9]。Yang 等[4]给出了导频与数据通道的相干组合捕获算法，并给出了一种并行捕获的实现结构。Mongredien 等[5]给出了一种数据与导频通道的非相干组合捕获算法，并对其性能进行了深入分析。Hegarty[6]对比了相干与非相干组合算法的性能，指出在高载噪比下相干组合算法优于非相干组合算法，但是，在低载噪比下，非相干组合算法优于相干组合算法。Borio[7]给出了一种导频/数据通道的差分组合算法，并将该组合算法和相干组合，非相干组合算法的性能进行比较，结果表明差分组合算法的性能弱于相干组合和非相干组合算法的结论。Ta等[8]针对E1 信号，对导频与数据通道的3 种组合算法作了进一步的深入研究，给出了3 种组合检测量的检测性能的近似推导结果和仿真验证性能，得出了在无数据辅助的情况下，当载噪比大于24 dB·Hz 时，相干组合算法优于其他2 种组合算法；当载噪比低于24 dB·Hz 时，非相干组合算法性能最好。上述文献在分析比较不同组合检测量的检测性能时并未根据信号的参数进行中频积累时间的最优设计，也没有考虑信号多普勒等因素对不同组合算法性能的影响，因此，分析不够全面。在传统导航信号的捕获研究领域，很多文献均提到了中频积累时间的优化问题，并给出了一种有效的优化方法[10-13]。其中文献[10]给出了在包络检波下的非相干积累时的中频积累时间的优化设计方法，文献[11]给出了在平方律检波下的非相干积累时的最优中频积累时间的优化设计方法，并将优化结果与同等条件下包络检波的最优设计性能进行了比较，得出了包络检波的性能优于平方律检波的结论；文献[12]深入讨论了差分后积累时最优中频积累时间的优化问题，并将其与同等条件下的包络检波下的非相干后积累的性能进行了比较，得出了差分后积累的性能优于非相干后积累。对于含导频信号的组合捕获算法，同样存在最优中频积累时间的优化问题。在此，本文作者建立导航信号的一般检测模型，给出已有的非相干组合检测量、差分组合检测量和相干组合检测量，证明了相干组合检测量是非相干组合和差分组合检测量的一种二次组合，在此基础上设计一种通用的组合捕获检测量，使得上述3 种检测量均是该通用组合捕获检测量的一种特殊形式。在分段相干-视频积累优化的方法的基础上给出了该通用组合检测量的一种二维优化模型，并在给定输入参数的情况下得出最优参数，在此基础上讨论最优参数随输入信号载噪比、最大多普勒容限以及导频功率系数的变化规律。

1 信号检测模型

本文以导频与数据通道正交的情况为例进行讨论，实际上所用方法和结论也适用于导频与数据通道同相的情况。信号检测的一般模型如图1 所示。

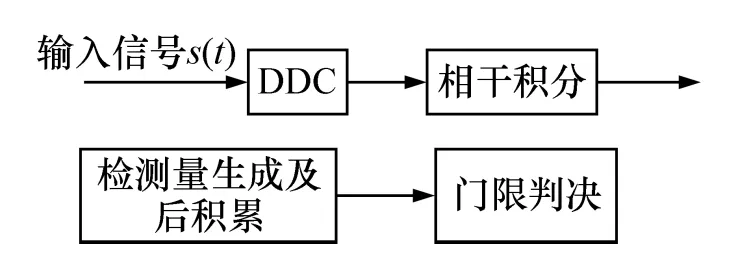
图1 导航信号检测的一般模型Fig.1 Model of signal detection

记输入捕获模块的中频信号为

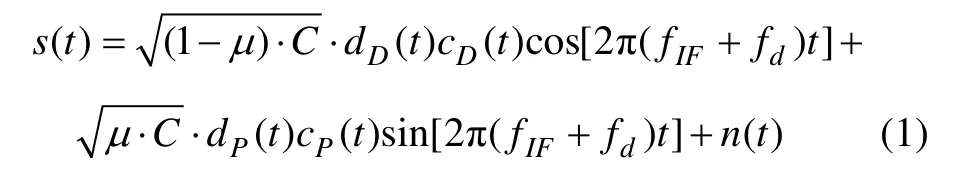
其中：μ 为导频通道的功率和整个信号功率的比，简称导频功率系数，0≤μ≤1；dD(t)为数据通道上的导航电文；dP(t)为导频通道上的二级码，通常二级码速率小于等于电文速率；cD(t)和cP(t)分别为数据和导频通道伪随机码；C 为信号功率；n(t)为带限高斯白噪声，双边带功率谱密度为N0，方差满足σn2=N0·Fs，则输入信号载噪比RCN=C/(2N0)。

中频信号通过正交下变频后在一个PIT(预检测积分时间)内与本地复现的伪码信号作相干积分，得到相应的相关值，如图2 所示。

对含导频通道的GNSS 信号，相干积分后共输出四路相关值信号，分别记为YD,I(τ，fd)，YP,I(τ，fd)， YD,Q(τ，fd)和YP,Q(τ，fd)，下标I/Q 表示I/Q 支路，D/P 表示数据/导频通道，其表达式如下：

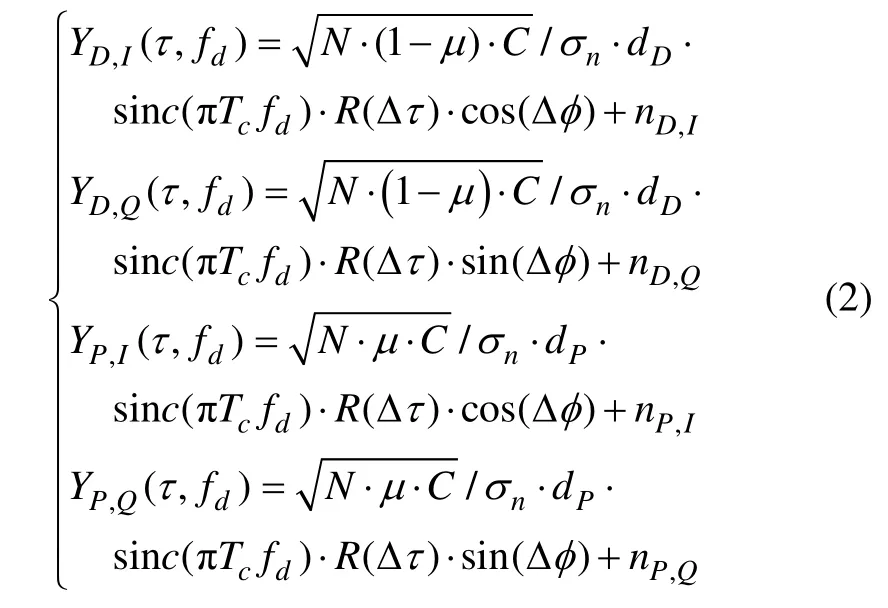
其中：nD,I，nD,Q，nP,I和nP,Q～N(0，1)为归一化后的噪声分量；Tc为相干积分时间(中频积累时间)；Fs为信号采样率；N=Tc·Fs为相干积分时间内的采样点数；R为伪随机码的自相关函数，忽略码相位偏移造成的损耗，则有R=1；ΔΦ 为数据与导频通道的残余相位，记L 为多普勒fd引起的相干损耗，则有L=sinc2(πTcfd)。相干积累后，经过K 次非相干后积累可得到最终检测统计量，其中K 为中频积累分段数，总的积分时间为T=Tc·K。

检测性能的好坏与检测量的设计及积累参数的选择密切相关，对传统导航信号，文献[10-13]从最优参数选择的角度给出了最优中频积累时间的一般优化方法。对含导频的导航信号，文献[4-9]通过设计不同的导频-数据通道的组合检测量以提高检测性能。实际上，对含导频的导航信号而言，依然存在最优中频积累时间的选择问题，因此，本文在不同组合检测量的基础上，证明了相干组合检测量是非相干组合检测量和差分检测量的一种组合，进而设计了一个由组合系数控制的通用的导频和数据通道的组合捕获检测量，然后利用分段相关-视频积累的优化方法，建立了该组合检测量的一个二维优化模型，通过对该优化问题的求解，可以得出不同条件下的最优设计参数。

2 通用组合检测量的设计

2.1 非相干组合检测量

非相干组合算法通过平方运算消除导频与数据通道上的相位残差及电文跳变的影响，然后对各分量进行能量积累。导频与数据通道的非相干组合原理如图所示。

第i 个PIT 内导频/数据通道的非相干组合可表示为

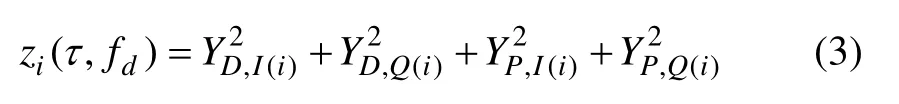
记有信号时为H1，无信号式为H0，则H1时zi服从非中心的Χ2(4)分布，H0时zi服从中心Χ2(4)分布。

非相干组合方式可以通过非相干方式进行后积累，即K 个PIT 检测量的累加和构成了最终的检测量，表达式为

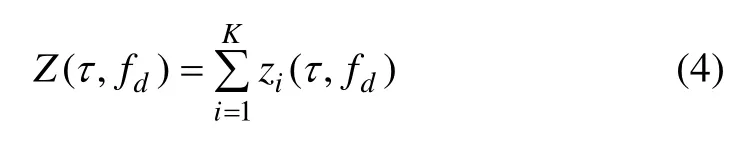
H1时Z 服从非中心的Χ2(4K)分布，H0时，Z 服从中心Χ2(4K)分布。

2.2 差分组合检测量

差分组合算法通过对导频和数据间作差分处理来消除导频与数据通道上的相位残差，通过取模消除电文的影响，实现能量的积累。导频和数据通道的差分组合原理如图3 所示。

第i 个PIT 内导频/数据通道的差分组合可表示为

后积累方式与非相干组合一样，如式(4)所示。根据中心极限定理可以近似得到H1和H0时检测统计量Z 的分布特性，具体可参考文献[7-8]。

2.3 相干组合检测量

相干组合在导频与数据通道间相对电文符号未知的情况下，通过二选一的取大方式，使得最终的检测量近似达到导频与数据通道间能量相干积累的效果。后积累方式采用非相干累积，相干组合算法如图4所示。

第i 个PIT 内相干组合检测统计量为

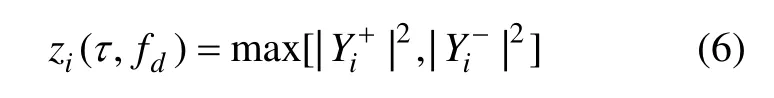
其中：

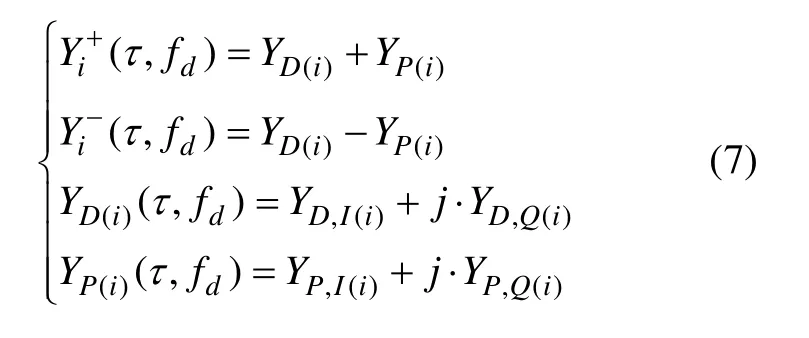
可见：该算法通过取大运算获得导频与数据通道在一个PIT 内的相对符号，实现导频与数据通道的相干积累。后积累K 次后所得检测量为对检测统计量Z 的统计特性的分析，可参考文献[7-8]。

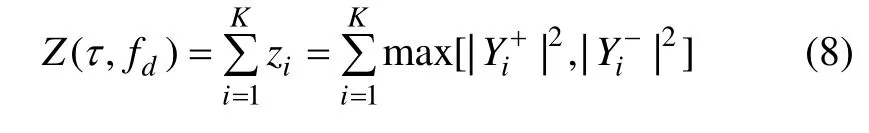
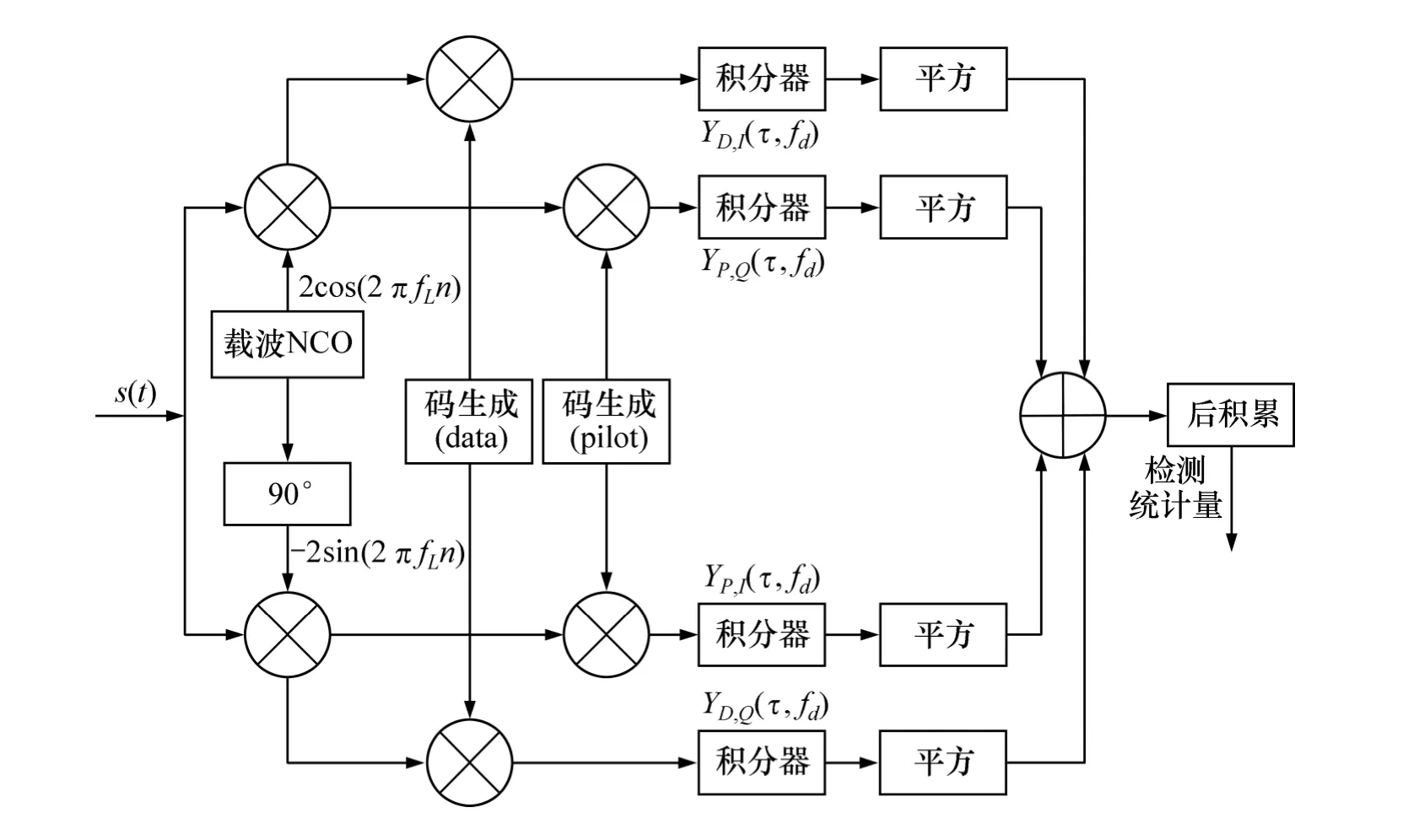
图2 导频与数据通道非相干组合捕获算法Fig.2 Pilot and data channel non-coherent combining acquisition algorithm

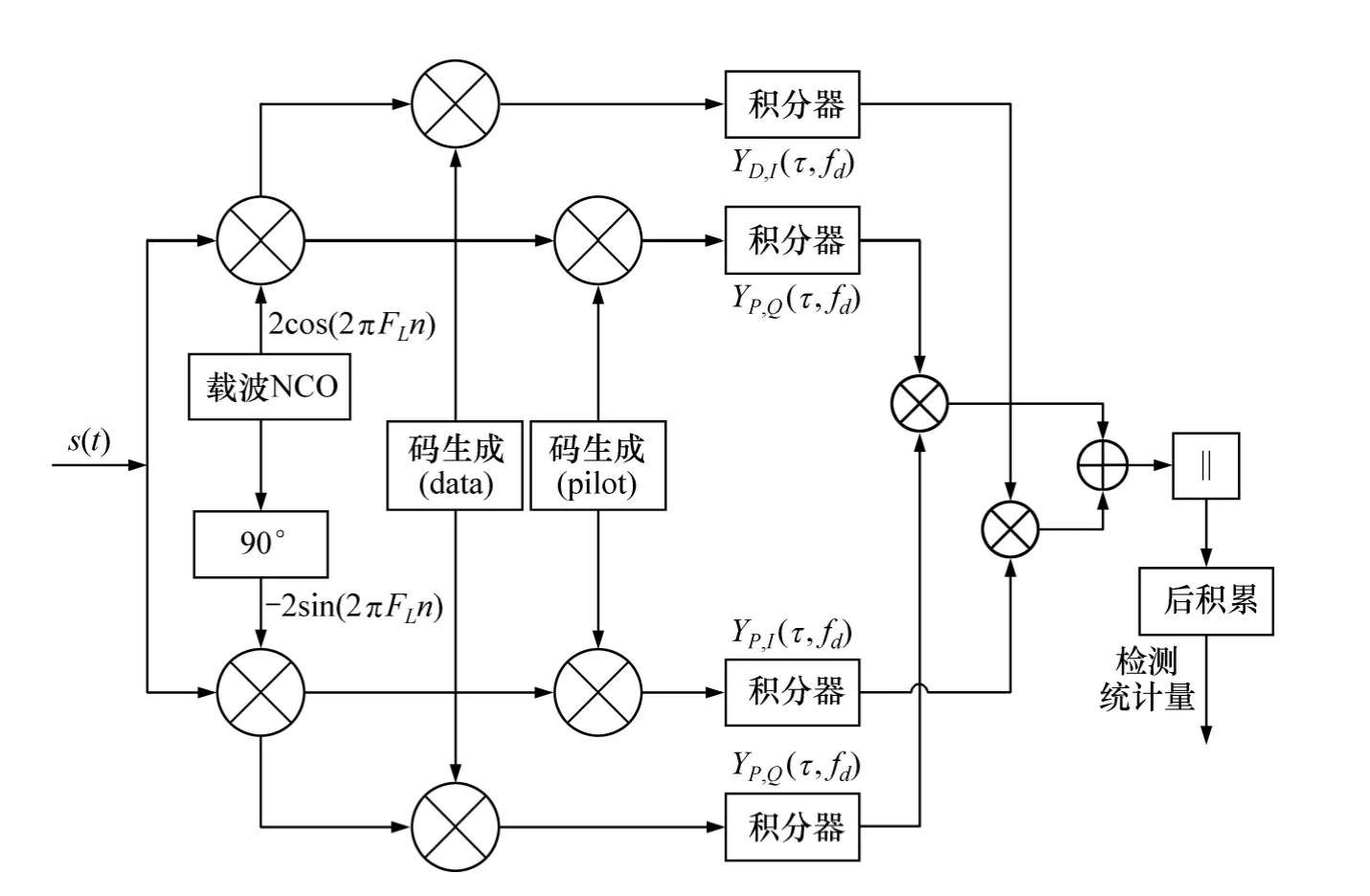
图3 导频与数据通道差分组合捕获算法Fig.3 Pilot and data channel differentially coherent combining acquisition algorithm

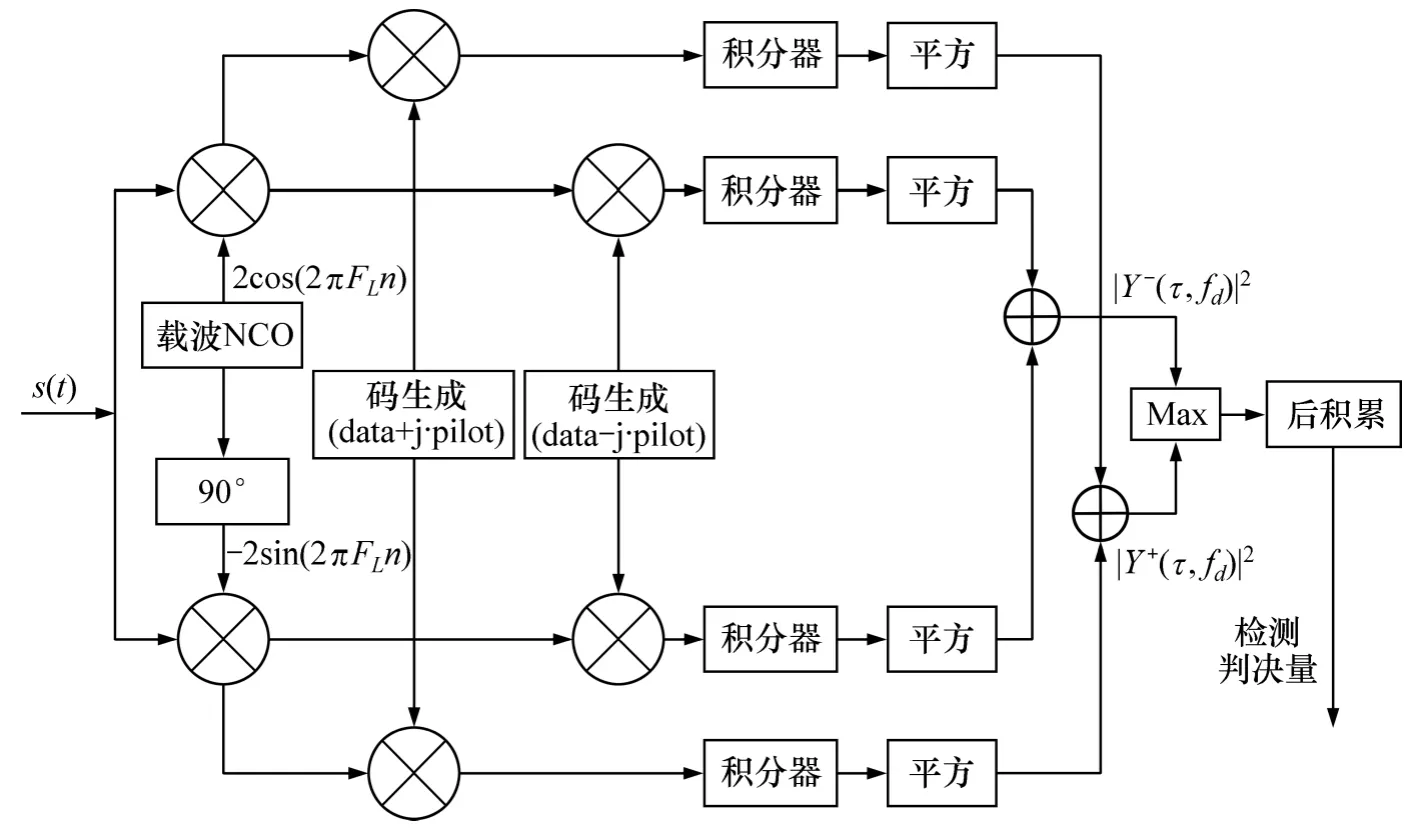
图4 导频与数据通道相干组合捕获算法Fig.4 Pilot and data channel semi-coherent combining acquisition algorithm

2.4 通用组合检测量

下面在相干检测量的基础上推导通用的导频与数据通道组合的捕获检测量。将式(7)代入式(6)可得

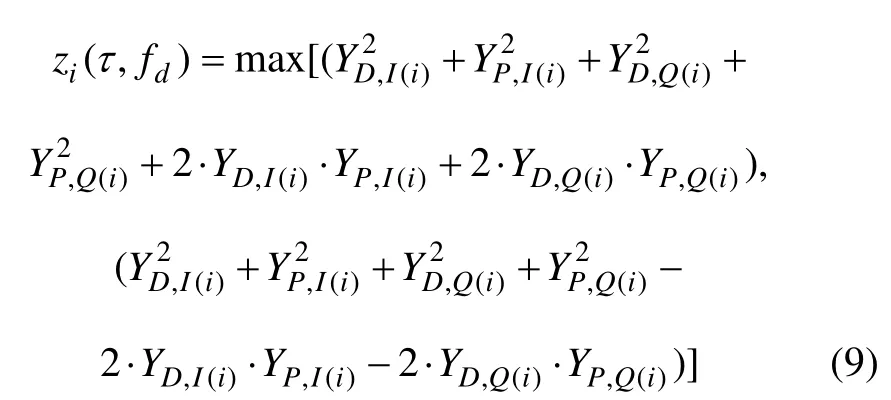
实际上，式(9)的取大操作可以直接用绝对值运算替代，即

由式(3)和式(5)可知：相干组合检测量实际上可以表示成非相干组合和差分组合的一种二次组合。由此可以给出含导频信号捕获的一种通用的组合捕获检测量的表达式为

其中：znon,i(τ，fd)和zdiff,i(τ，fd)分别为第i 次PIT 内的非相干组合和差分组合检测量；λ 为组合系数。实现结构如图5 所示。

图5 通用的导频与数据通道组合的捕获算法Fig.5 Universal pilot and data channel combining acquisition algorithm

后积累K 次后所得检测量为

由式(12)可知：

当λ=0 时，通用组合检测量退化为非相干组合检测量；

当λ=∞时，通用组合检测量退化为差分组合检测量；

当λ=2 时，通用组合检测量退化为相干组合检测量。

可以证明znon,i(τ，fd)和zdiff,i(τ，fd)之间是相关的，因此两者并不独立，这样，zi在H0和H1下统计特性的解析表达式将会变得比较复杂。为此，本文结合中频积累时间的优化方法给出该通用组合检测量的一种数值优化设计方法。

3 通用组合检测量的优化

3.1 优化参数

从通用组合检测量的表达式看，其检测性能和组合系数λ 有关，为了使得该检测量的检测性能最优，需要对组合系进行优化。由于不同组合系数下的检测量存在一个最优中频积累时间，因此，在对组合系数优化的同时需考虑最优中频积累时间，故该问题将转化选择合适的组合系数λ 和视频积累分段数K，使得通用组合检测量的检测性能最优。因此，优化参数设计为λ 和K。

3.2 目标函数

参考分段相关-视频积累的优化准则，将检测量的最大检测损耗作为优化目标。文献[14-15]给出了等效理想检测因子的概念，即达到相同检测性能时候对应的相干检测量的信噪比，其换算关系为

式中：

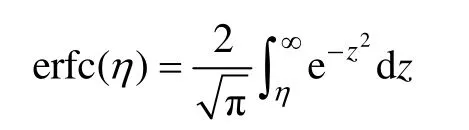
Pfa和Pd由检测量的统计特性决定。显然，在虚警概率相同时，等效理想检测因子越大，检测性能越强。

检测损耗定义为检测量的等效理想检测因子相对理想相干接收机的检测损耗，具体为

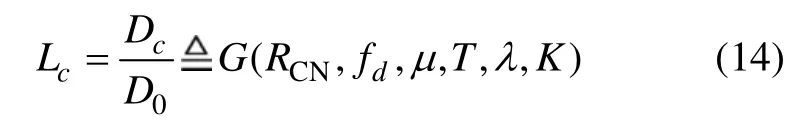
其中：Dc为理想相干接收机的检测因子。当fd为信号多普勒容限时，对应检测损耗最大，优化目标寻找最大检测损耗的最小值。

3.3 约束条件

针对恒虚警检测进行讨论，约束条件即为相应的虚警概率，另外考虑最长的相干积分时间不能超过1个电文或1 个二级码的长度，因此，分段数K 存在1个最小值的约束，本文讨论电文速率和二级码速率相同的情况，设1 个电文符号宽度为Td。

3.4 优化模型

根据优化参数、目标函数和约束条件，该优化问题可用下面模型描述

其中：N 为自然数集；RCN为输入信号载噪比；fd为最大的残留多普勒；μ 为导频通道占整个信号的功率比；T 为总积累时间。上述4 个参数表征检测量中输入信号的参数。λ 为通用检测量的组合系数；K 为后积累次数或中频积累的分段数，则相干积累时间Tc=T/K，K 要使得相干积分时间小于1 个电文宽度Td。Pfa0=1×10-5，Td=1 ms。为保证仿真结果的准确性，选择仿真次数为107次。

3.5 优化结果及分析

下面讨论一组典型参数下的优化结果，参数取值如表1 所示。

表1 输入信号参数表Table 1 Value of signal parameters

在信号参数给定的情况下，最大检测损耗是关于组合系数λ 和分段数K 的二维函数，该函数在整个λ和K 组成的二维域上存在一个最小值的点P(λ，K)，该点即为所求的最优设计点，对应的λ 和K 即为所得最优参数。仿真数值解的二维域由λ 和K 的离散点组成，其中λ 为从0 到4 以0.2 为间隔步进增加，K 为从5 到20 以1 为间隔步进增加。最大检测损耗关于λ和K 的变化关系如图6 所示。由图6 可知：在上述参数下，最优的参数选择为λ=1.6，K=11，此时最大检测损耗为4.296 2 dB。

图7 所示为上述二维优化模型退化为2 个一维模型时的优化结果。由图7 可知：在固定λ 的情况下，该优化问题与文献[10-13]中给所给的最优中频积累时间的优化结果一致的，优化效果较明显；在固定K及λ 取不同值时，该问题退化为文献[7-8]中的3 种组合检测量的性能比较。另外，从图7(a)可以看出：最优组合系数的优化空间并不是很大，相比非相干组合算法，只提高0.2 dB 左右，比相干组合算法提高约0.05 dB。

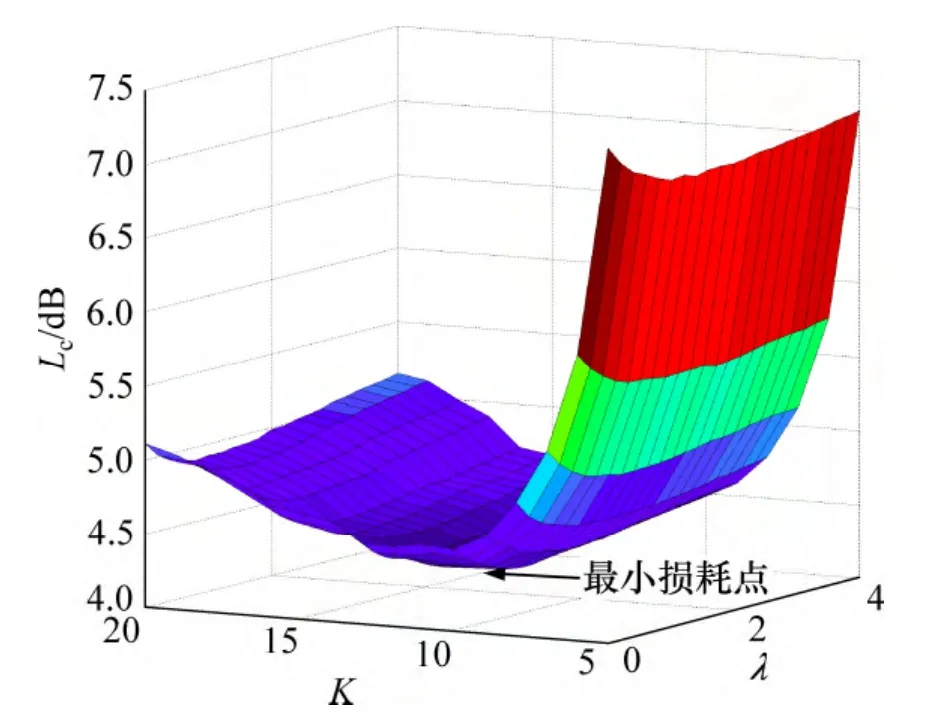
图6 最大检测损耗随λ 和K 的变化Fig.6 Maximum detection loss in different λ and K

图7 一维优化模型的参数优化Fig.7 Optimum parameter of one dimension model

下面分别讨论最优参数λ 和K 随信号参数RCN，fd以及μ 的变化规律。

3.5.1 最优参数与输入载噪比的关系

下面分析输入信号多普勒容限最大为500 Hz，导频功率系数为0.5，总积分时间为5 ms，载噪比从33～42 dB·Hz 变化时检测量的最优参数及最大损耗的最小值。

表2 所示为最优设计参数随输入信号载噪比的变化关系。由表2 可见：最优组合系数和最优分段数基本上满足随着信号载噪比的增加而增加的变化规律，最大损耗随信号载噪比的增加而减小。

根据上面的优化结果，可以得出：高载噪比下，增加λ 和K 有利于提升通用检测量的检测性能；低载噪比下，减小λ 和K 有利于提高检测量的检测性能。这与文献[8]和[11]所给结论是一致的。

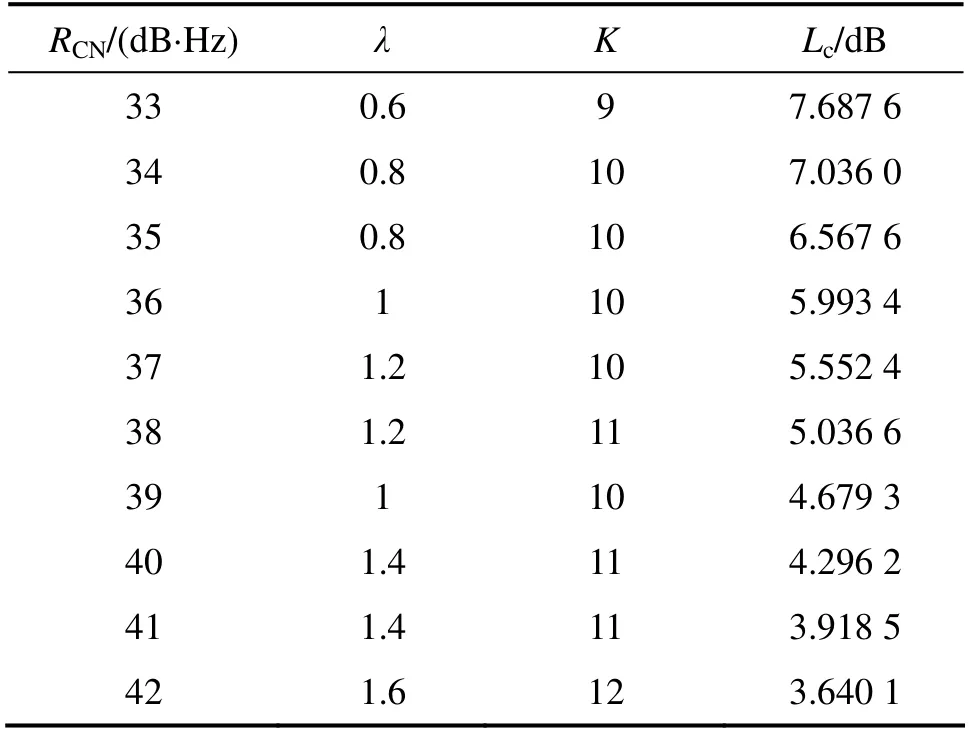
表2 不同载噪比下的最优设计参数Table 2 Optimum parameters in different CNR

3.5.2 最优参数与多普勒容限的关系

下面分析输入信号载噪比为40 dB·Hz，导频功率系数为0.5，总积分时间为5 ms，多普勒容限从200～1 000 Hz 变化时检测量的最优参数及最大损耗的最小值。

表3 所示为不同多普勒容限下的最优设计参数。可以看出，随多普勒容限的增加，最优组合系数逐渐减小，最优分段数逐渐增加，相应的最大损耗逐渐增加。

随着多普勒容限的增加，为抵抗多普勒损耗的增加，需增加分段数，减小相干积分时间[11]。但实际上从优化结果上看最大损耗依然呈现增加的趋势，这相当于输入信号载噪比降低。根据前面的分析，最优组合系数应呈减小的趋势，仿真结果与此吻合。

据此可以得出在多普勒容限较大时，小的组合系数和大的分段数有利于提高检测性能，多普勒容限小时，大的组合系数和小的分段数有利于提高检测性能。

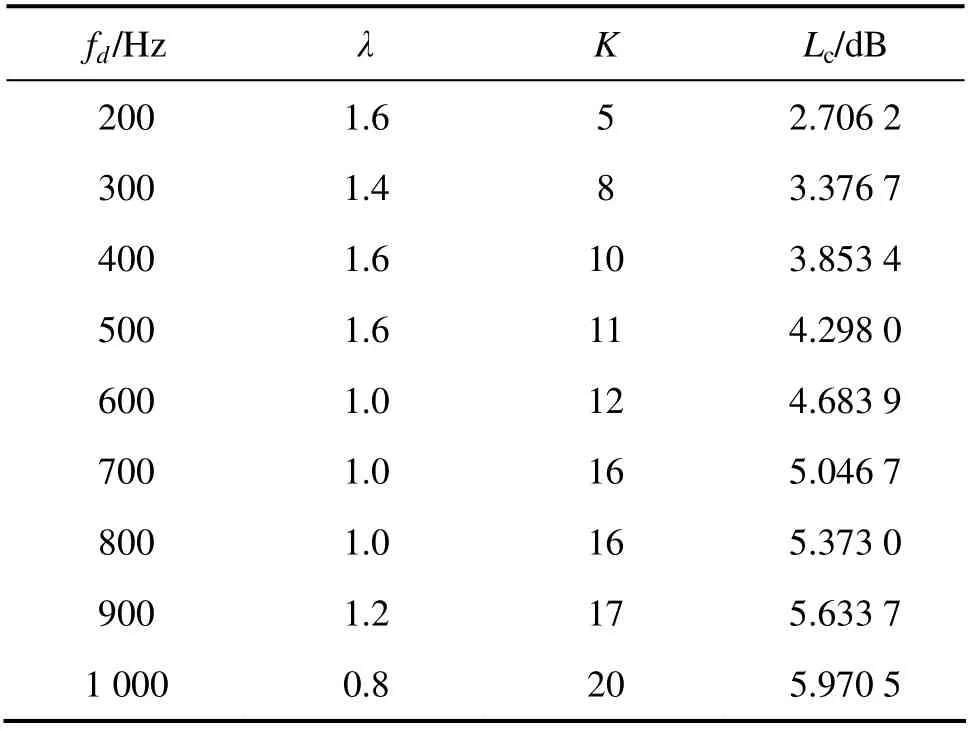
表3 不同多普勒容限下的最优设计参数Table 3 Optimum parameters in different fd

3.5.3 最优参数与导频功率系数的关系

下面分析输入信号载噪比为40 dBHz，多普勒容限500 Hz，总积分时间为5 ms，导频功率系数为从0.1～0.9 变化时检测量的最优设计点及相应的最大检测损耗。

表4 所示为不同导频功率系数下的最优设计参数。从表4 可以看出：最优分段数和导频信号功率比无明显的关系；最优组合系数随导频功率系数现增加后减小的趋势变化，在μ=0.5 左右达到最大；相应地，最大检测损耗呈先减小后增加的趋势，在μ=0.5 左右时达到最小。

表4 不同导频功率系数下的最优设计参数Table 4 Optimum parameters in different μ

上述数值解是在导频上次级码速率与电文速率相同时所得的最优设计参数。当相干积累时间小于一个电文宽度时，对捕获而言，导频通道和数据通道是一样的，因此，理论上最优组合系数和最大检测损耗关于导频功率以0.5 呈偶对称，从仿真结果来看，大致满足这一关系。

4 结论

(1) 本文证明了导频与数据通道的相干组合检测量是非相干组合检测量和差分组合检测量的二次组合形式，在此基础上设计了一种通用的导频与数据通道的组合检测量。

(2) 利用分段相关-视频积累的优化方法，对该组合检测量的检测性能进行优化设计，优化后的性能优于非相干组合检测量、差分组合检测量和相干组合检测量。

(3) 分析并给出了通用组合检测量中的组合系数和最优分段数随输入信号载噪比、多普勒容限和导频信号功率系数的变化规律。

(4) 本文结论可以用于指导含导频的GNSS 信号的捕获算法设计，亦可用来指导含导频的扩频信号的接收设计。

[1] 胡修林, 唐祖平, 周鸿伟, 等. GPS 和Galileo 信号体制设计思想综述[J]. 系统工程与电子技术, 2009, 31(10): 2285-2293.HU Xiulin, TANG Zuping, ZHOU Hongwei, et al. Analysis on design principles of GPS and Galileo signal structure[J]. Systems Engineering and Electronics, 2009, 31(10): 2285-2293.

[2] Galileo OS SIS ICD: Galileo Open Service, signal in Space Interface Control Document Draft1. European GNSS Supervisory Authority/European Space Agency [EB/OL].[2008-02-01]. http://www.gsa.europa.eu/

[3] IS-GPS-705A, Navstar GPS Space Segment/User Segment L5 Interfaces Specification[S].

[4] YANG Chun, Hegarty C, Tran M. Acquisition of the GPS L5 Signal Using Coherent Combining of I5 and Q5[C]//California:The Institute of Navigation, 2004: 2184-2195.

[5] Mongredien C, Lachapelle G, Cannon M E. Testing GPS L5 acquisition and tracking algorithms using a hardware simulator[C]//Texas: The Institute of Navigation, 2006:2901-2913.

[6] Hegarty P C J. Optimal and near-optimal detector for acqusition of GPS L5 signal[C]//California: The Institute of Navigation,2006: 717-725.

[7] Borio D. A statistical theory for GNSS signal acquisition[D].Torino, Italy: Politecnico di Torino, 2008: 109-119.

[8] Ta T H, Dovis F, Margaria D, et al. Comparative study on joint data/pilot strategies for high sensitivity Galileo E1 open service signal acquisition[J]. The Institution of Engineering and Technology, 2010, 4(6): 764-799.

[9] Borio D, Presti L L. Data and pilot combining for composite GNSS signal acquisition[EB/OL]. [2008-12-01]. http://dx.doj.org/10.1155/2008/738183

[10] 王飞雪, 郭桂蓉. 二相编码信号分段相关-视频积累的最优中频积累时间[J]. 国防科技大学学报, 1999, 21(1): 71-75.WANG Feixue, GUO Guirong. The optimum IF integration time length for binary phase-code signals detection based on segment correlation-video integration method[J]. Journal of NUDT, 1999,21(1): 71-75.

[11] 朱祥维, 王飞雪. 基于平方律检波的二相编码信号分段相关-视频积累方法研究[J]. 电子学报, 2005, 33(3): 545-548.ZHU Xiangwei WANG Feixue. Study on segment correlation-video integration method using square-law detector for binary phase-code signal detection[J]. Acta Electronica Sinica, 2005, 33(3): 545-548.

[12] 刘文祥, 彭竞, 王飞雪. 基于差分相干后积累的伪码信号检测方法优化与分析[J]. 宇航学报, 2011, 32(7): 1576-1582.LIU Wenxiang, PENG Jing, WANG Feixue. Optimization and analysis of differential coherent post detection integration method for PN code signal detecting[J]. Journal of Astronautics,2011, 32(7): 1576-1582.

[13] 许晓勇, 唐小妹, 王飞雪. 基于分段相关-视频积累方法的伪码串行捕获优化设计[J]. 信号处理, 2009, 25(9): 1338-1341.XU Xiaoyong, TANG Xiaomei, WANG Feixue. Optimum design of serial PN code acquisition using segment correlation-video integration method[J]. Signal Processing, 2009, 25(9):1338-1341.

[14] Barton D K. Simple procedures for radar detection calculations[J]. IEEE Trans AES, 1969, 5(5): 837-846.

[15] Barton D K. Modern radar system analysis[M]. London: Artech House, 1969: 57-95.