基于压力角的高重合度齿轮主动设计及特性分析

王建，罗善明，苏德瑜

(1. 厦门理工学院 机械与汽车工程学院，福建 厦门，361024；2. 湖南科技大学 机电工程学院，湖南 湘潭，411201)

重合度是衡量齿轮副的传动连续性、平稳性、传递载荷均匀性的重要度量指标，其定义是齿轮副的一对轮齿从开始啮合到终止啮合过程中，某一齿轮所转过的角度与该齿轮单个齿距圆心角的比值。它所表达的是齿轮副的平均啮合齿对数的信息[1-2]。齿轮传动的重合度不仅与传动的回转误差有关，还对齿轮强度有着重要的影响，而且为了保证能进行连续传动，必须满足重合度大于1 的条件。为了提高齿轮传动的承载能力和动态性能，目前采用重合度大于2 的高重合度齿轮传动[3-5]。与常规的齿轮传动相比，高重合度齿轮传动的同时啮合轮齿对数较多，因此承载能力大[6]。高重合度直齿圆柱齿轮的设计，一般是通过增大齿顶高系数、增大齿数、减小压力角等方法来实现[7]。增大齿顶高系数可以显著提高齿轮副的重合度，但会导致齿顶厚减小使齿顶变尖，容易引起靠近齿顶的部位发生崩齿。齿轮副齿数增大重合度也会增加，但会使齿轮传动体积增大。减小压力角可使重合度增大，且能增大齿厚，减小轮齿变尖的可能，但是在满足重合度要求的基础上，要尽量选择较大的压力角，以减小弯曲和接触应力，提高齿轮传动的强度。上述高重合度齿轮的设计方法都属于被动设计方法，无法实现通过改变预先给定的齿轮传动重合度主动控制齿廓形状的目的。为了满足航空和汽车领域中齿轮传动的高平稳性和高重合度需求，本文作者提出了一种基于压力角的高重合度齿轮主动设计方法，即在建立的压力角为一次函数时齿廓方程描述方法的基础上，首先给定齿轮传动的重合度，根据齿轮啮合原理，推导齿廓的形状，从而达到通过改变重合度主动控制齿廓形状的目的。

1 基于压力角的齿廓方程的数学描述

齿轮啮合坐标系如图1 所示。齿轮1 与坐标系Σ 1(O1,x1,y1)相固联，齿轮2 与坐标系Σ2(O2,x2,y2)相固联，通过节点P 的曲线为啮合线。假设两齿廓接触点从P 移动到P1位置，则P1位置的接触点在坐标系Σ 0(O0,x0,y0)下的坐标可表示为

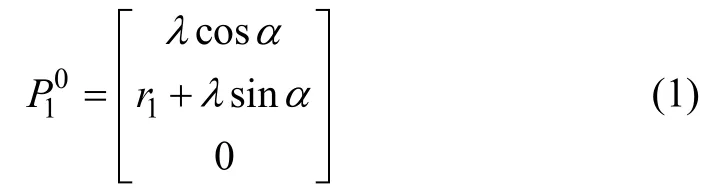
其中：λ 为极距；α 为压力角；r1为齿轮1 的节圆半径。

若齿轮1 顺时针旋转一个角度φ，坐标系Σ1(O1,x1,y1)也随着齿轮1 旋转一个角度到达图示位置，则P1点在坐标系Σ1(O1,x1,y1)下的坐标可表示为

同样地，将接触点在坐标系Σ1(O1,x1,y1)中的坐标变换到坐标系Σ2(O2,x2,y2)下，可得齿轮2 的齿廓方程为

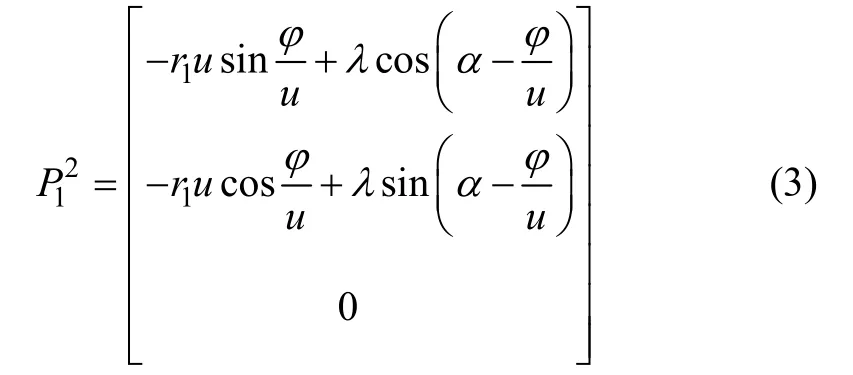
其中：u 为齿轮传动比。

当φ 取正值时，式(2)和式(3)分别代表齿轮1 齿廓齿顶部分和齿轮2 齿廓齿根部分的坐标方程，而当φ取负值时，分别代表齿轮1 齿廓齿根部分和齿轮2 齿廓齿顶部分的坐标方程，同时，极距λ 和压力角α 都分别是转角φ 的函数。

根据齿轮啮合原理，齿廓上接触点的法向量和切向量应相互垂直，即

其中：τ11为接触点P1在齿轮1 齿廓上的切向量；n11为接触点P1在齿轮1 齿廓上的法向量。

根据图1 和式(2)，式(4)可化简整理为

要使两齿轮正确啮合，齿轮2 齿廓上接触点的法向量和切向量也应相互垂直，同样可计算得式(5)成立。

由式(2)，(3)和(5)可知，若压力角α 也能表示成φ的函数，则式(2)和(3)分别表示相互啮合的两齿轮即齿轮1 和齿轮2 的齿廓方程。

2 以压力角描述的齿轮啮合特性的定量表达式

2.1 曲率

齿轮1 上接触点的曲率为[8]

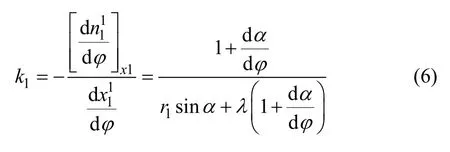
同理可得，齿轮2 上接触点的曲率为

由式(6)和(7)可知，当曲率为正值时，齿廓为凸齿廓，因此，齿廓上尖点存在的条件为曲率半径为0，即

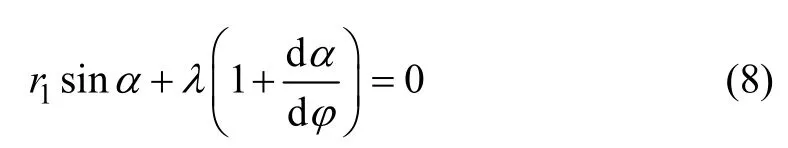
2.2 滑动系数

根据齿轮啮合原理，齿轮1 和2 的滑动系数可表示为[9]

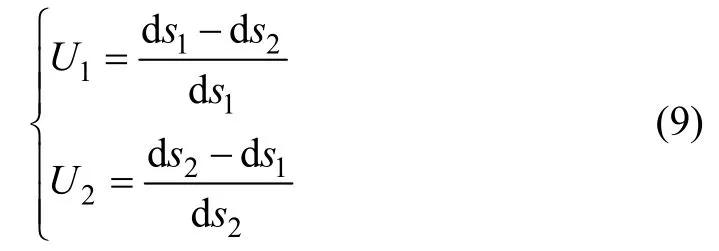
其中，

将式(10)和(11)代入式(9)可得，齿轮1 和2 的滑动系数为

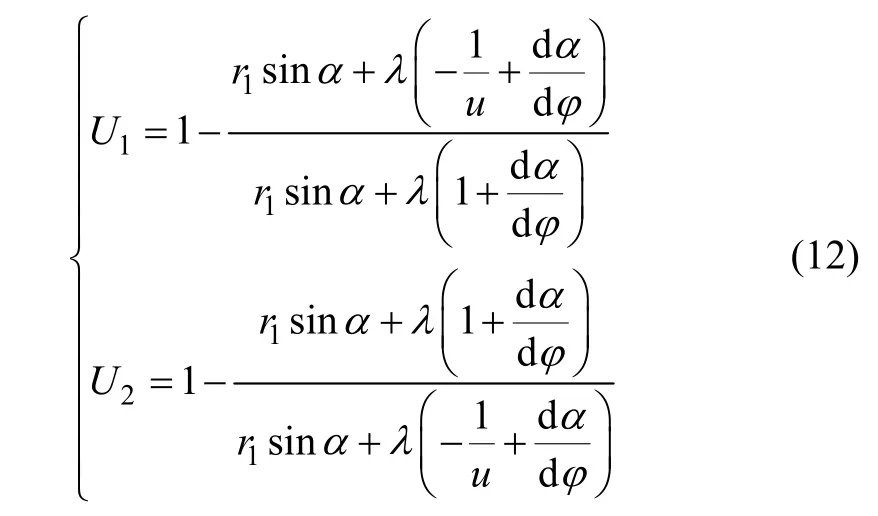
2.3 重合度

齿轮的重合度可表示为[10-11]

其中：z1为齿轮1 的齿数。

假设齿轮的α 可表示为φ 的一次函数，即

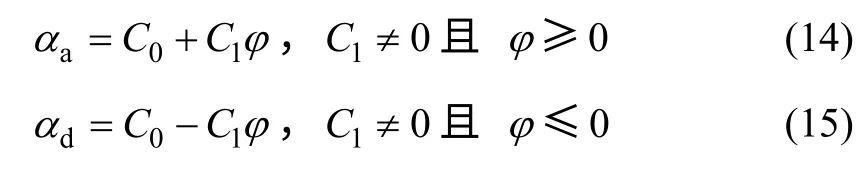
其中：C0和C1分别为一次函数的系数； αa为节圆和齿顶圆之间齿廓上点的压力角；αd为节圆和齿根圆之间齿廓上点的压力角。

当两齿轮的一对轮齿开始啮合时，必为主动轮的齿根推动从动轮的齿顶。因此，开始时啮合点是从动轮的齿顶与啮合线的交点(如图1(a)所示)，随着啮合传动的进行，结束时的啮合点是主动轮的齿顶与啮合线的交点(如图1(b)所示)，为了方便计算，以节点处为参考点。

由图1 可知，下式成立：

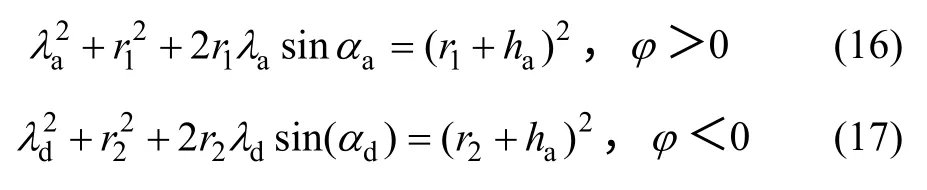
其中：r1和r2分别表示齿轮1 和齿轮2 的分度圆半径；λa表示节圆和齿顶圆之间齿廓上的点对应的极距；λd表示节圆和齿根圆之间齿廓上的点对应的极距。

当齿轮1 的模数m，齿数z1，传动比u，齿顶高ha，压力角的函数表达式已知时，根据式(14)和式(16)可求得接触点位于齿廓顶部时对应的φa(φa＞0)的大小，根据式(15)和式(17)可求得接触点位于齿廓根部时对应的φd(φd＜0)。将其代入式(13)，可计算得齿轮传动的重合度。

3 高重合度齿廓主动设计数学模型的建立

一元二次方程(16)和(17)根的存在条件为

由图1 可知：压力角范围为[0,π/2]，而当φ=0 时，α=C0±C1φ 表 示 分 度 圆 上 的 压 力 角，因 此C0满 足0≤C0≤π/2。

当C0=0，将C0=0 代入式(14)，(15)，(5)和(8)可知，当φ=0 时，不管C1取何值，齿廓都会存在尖点。因此，C0=0 这种情况不适合设计齿轮齿廓。

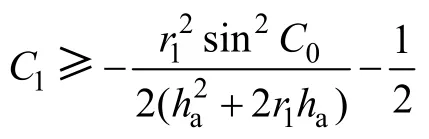
当C1在上述范围内，且C1＜0 时， φa和 φd的取值范围分别为

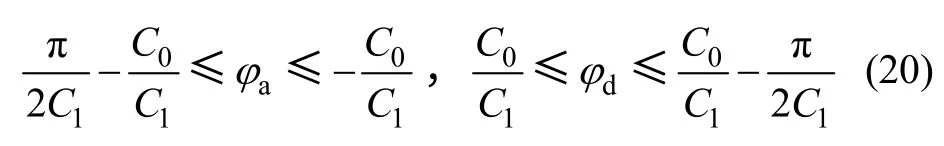
而当C1＞0 时， φa和 φd的取值范围分别为

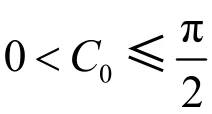
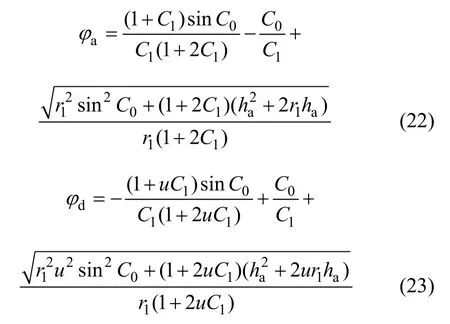
将式(22)和式(23)代入式(13)，即可计算得齿轮的重合度。同理，当齿轮的模数m，齿数z1，传动比u，齿顶高系数ha*，顶隙系数C*，系数C0已知时，根据式(22)、式(23)和式(13)，可画出系数C1和重合度ε的关系曲线。根据该曲线关系，当重合度确定后，可选择系数C0和C1，将C0和C1分别代入式(14)，(15)和(5)，可计算得α 和λ，将上述数值代入式(8)验证是否出现尖点，若不出现尖点，则可将上述数值分别代入式(2)和(3)可得主动齿廓和从动齿廓的表达式；若出现尖点，则需重新选择系数C0和C1。

4 设计实例

4.1 齿廓方程

为了验证上述设计方法的正确性，以重合度为3.0的齿轮传动为例，说明其具体设计过程。齿轮的其他参数为模数m=2.5，齿顶高系数ha*=1，顶隙系数C*=0.25，齿数z1=25，z2=39。根据式(22)、式(23)和式(13)，若选取C0为π/8 和π/16，则系数C1和重合度ε的关系曲线如图2 所示。当齿轮的重合度为3.0 时，本文选取C0=π/8，从而可得C1=0.539 9。将C0=π/8 和C1=0.539 9 代入式(14)，(15)和(5)，可计算得α 和λ，将上述数值代入式(8)可知，齿廓不会出现尖点。因此，将上述数值分别代入式(2)和式(3)可得主动齿廓和从动齿廓的方程分别为

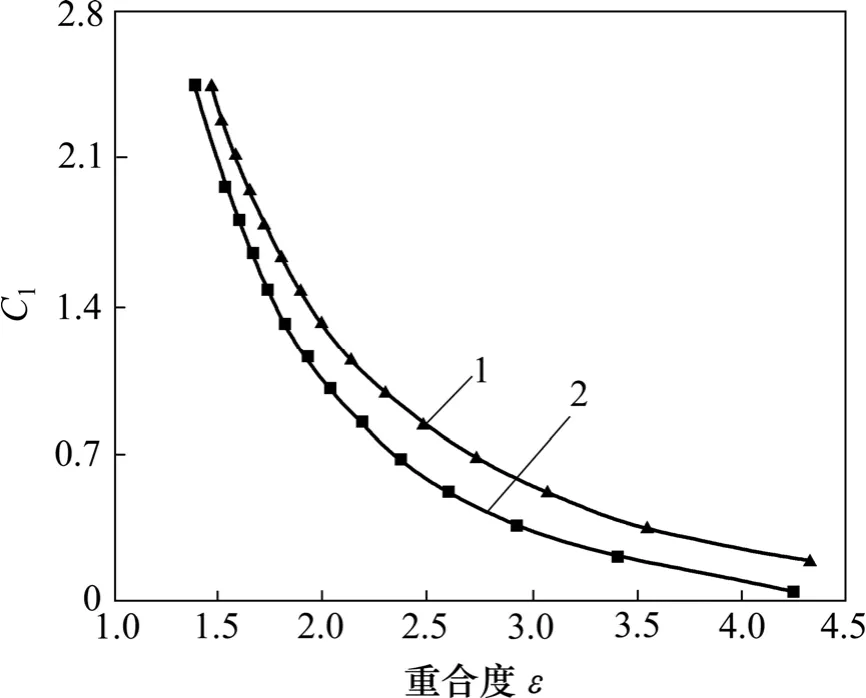
图2 系数C1 和重合度ε的关系曲线Fig.2 Relationship between contact ratio ε and coefficient C1

图3 所示为高重合度齿轮与渐开线齿轮齿廓对比图，其中，虚线为渐开线齿廓，实线为高重合度齿廓。由图3、式(24)和式(25)可知：

1) 当φ≥0 时，式(24)和式(25)的第1 个式子分别表示主动齿轮分度圆和齿顶圆之间的齿廓、从动齿廓齿根圆和分度圆之间的齿廓；而当φ≤0 时，式(24)和式(25)的第2 个式子分别表示主动齿轮分度圆和齿根圆之间的齿廓以及从动齿廓齿顶圆和分度圆之间的齿廓。

2) 与相同参数的渐开线齿廓相比，高重合度齿轮在分度圆以下部分的齿宽大于渐开线齿轮在分度圆以下部分的齿宽，而在分度圆以上部分则相反。

图3 齿廓对比图Fig.3 Tooth profiles of gears

4.2 曲率

根据式(6)和(7)，利用MATLAB 软件，可得出齿廓的曲率随转角φ的变化曲线，如图4 所示。其中实线表示主动齿廓的曲率，虚线表示从动齿廓的曲率。综合曲率半径是衡量齿轮接触强度的重要指标，与齿廓接触应力和接触强度有着密切的关系，因此有必要找出高重合度齿轮综合曲率半径的变化曲线。

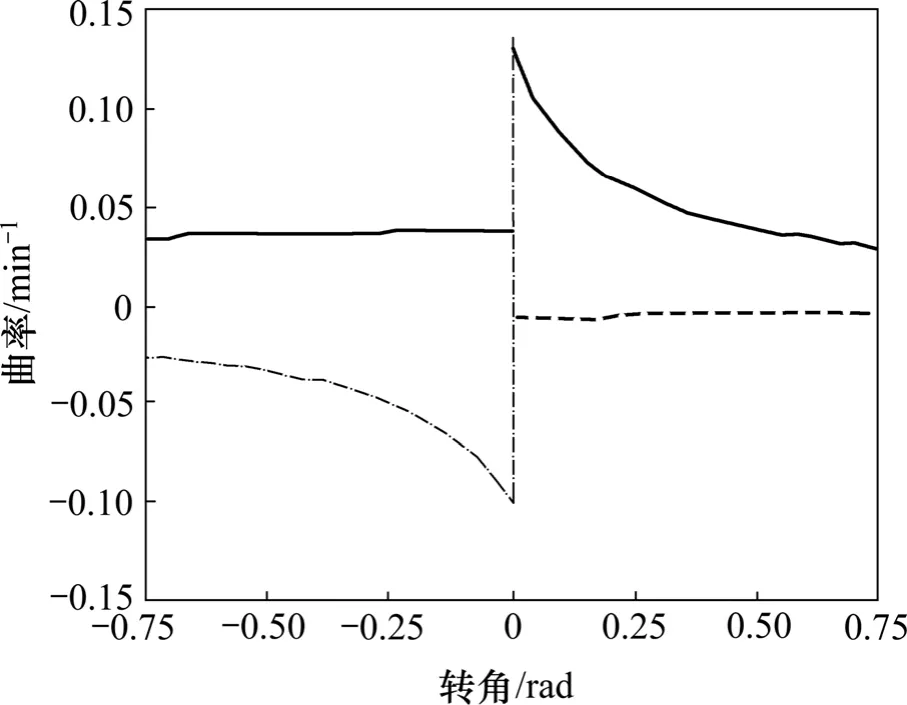
图4 齿廓曲率随齿轮转角的变化曲线Fig.4 Curvature of tooth profiles with different rotation angles

综合曲率半径ρ可表示为[12]：

当接触部分曲率方向相同时取“-”号，相反则取“+”号。

图5 所示为高重合度齿轮综合曲率半径随转角φ的变化曲线。由图5 可知：高重合度齿轮的综合曲率半径很大，根据赫兹公式，两轮齿在接触处的最大接触应力与综合曲率半径成反比[13]，故高重合度齿轮在接触点处的最大接触应力较小，对应的接触强度会相应较大。

4.3 滑动系数

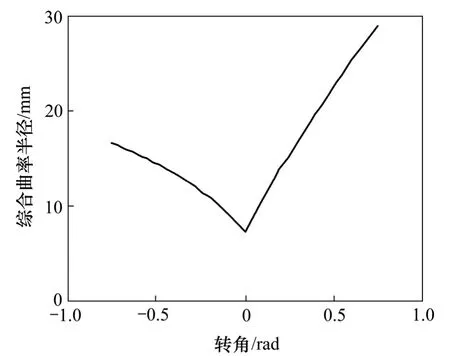
图5 高重合度齿轮的综合曲率半径Fig.5 Composite curvature radius of proposed gear

图6 高重合度齿轮的滑动系数Fig.6 Sliding coefficients of proposed gear drive

根据式(12)绘制高重合度齿轮的滑动系数如图6所示。当φ＞0 时，可绘制主动齿轮分度圆与齿顶圆之间齿廓的滑动系数以及从动齿轮分度圆和齿根圆之间的滑动系数，而当φ＜0 时，可绘制主动齿轮分度圆与齿根圆之间齿廓的滑动系数以及从动齿轮分度圆和齿顶圆之间的滑动系数。

当压力角为常数时，齿廓为渐开线齿廓[14]，若渐开线齿轮的压力角为20°，其他参数和高重合度齿轮相同，则C0=π/9，C1=0。根据式(12) 绘制渐开线齿轮的滑动系数，如图7 所示。

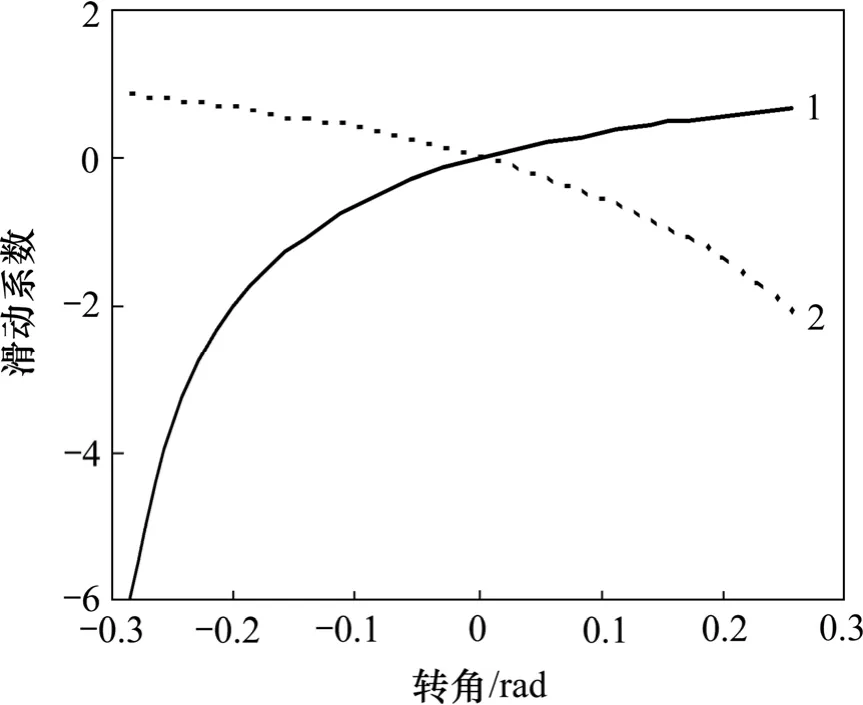
图7 渐开线齿轮的滑动系数Fig.7 Sliding coefficients of involute gear drive

由图6 和图7 可知：节圆处滑动系数为0，而在远离节圆处，滑动系数逐渐增大，表示齿面磨损量增大；高重合度齿轮主动轮的滑动系数变化区间为[-2.33, 0.61]，从动轮的滑动系数变化区间为[-1.55,0.70]，而渐开线齿轮主动轮的滑动系数变化区间为[-5.98, 0.68]，从动轮的滑动系数变化区间为[-2.12,0.86]，因此，高重合度齿轮的滑动系数远远小于渐开线齿轮的滑动系数，有利于改善齿轮的磨损状况，提高齿轮的寿命。

5 动力学分析

为了分析重合度对齿轮动力学特性的影响，根据Hertz 碰撞理论，本文利用Adams 软件，对设计实例中的高重合度齿轮进行了动力学分析。分别在两齿轮上施加旋转副，齿轮之间加实体-实体碰撞力，输入轴上加转速驱动，输出轴上加负载转矩，建立的完整动力学仿真模型如图8 所示。

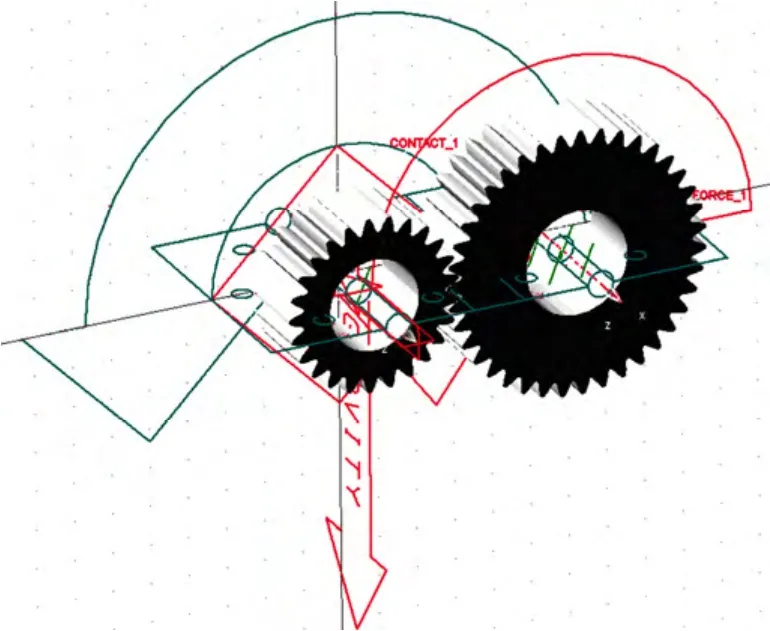
图8 动力学仿真模型Fig.8 Dynamic simulation model

小齿轮施加的转速为300 r/min，为了避免由于开始的冲击造成的速度突变，转速驱动以阶跃函数施加，为STEP(time，0，0d，0.2，1 800d)。在被动齿轮的转动轴上施加的负载函数为STEP(time，0，0，0.01，150 000)，大小为150 N·m 的阶跃函数。接触碰撞函数可表示为IMPACT(x，x，x1，k，e，Cmax，d)[15]，其中，x 表示用来计算碰撞函数里的距离变量；x相对于位移的碰撞速度；x1表示位移x 自由长度的正实数变量，若x＜x1则力赋一个正值，否则力为0 N，x1可以被定义为一个实数、函数或者变量；e 表示力的变形特性指数的一个正实变量；Cmax表示最大阻尼系数的一个非负实变量；d 表示在施加全阻尼时的边界穿透量。根据设计实例中齿轮参数可计算得阻尼系数C=50 N·s/mm，穿透深度d=0.1mm，k=6.4×105N/mm，e=1.5。本文取仿真时间为0.5 s，步长为6 000。图9所示为高重合度齿轮啮合力仿真曲线。为了便于比较，图10 给出了相同参数的渐开线齿轮的啮合力仿真曲线。由图9 和图10 可知：

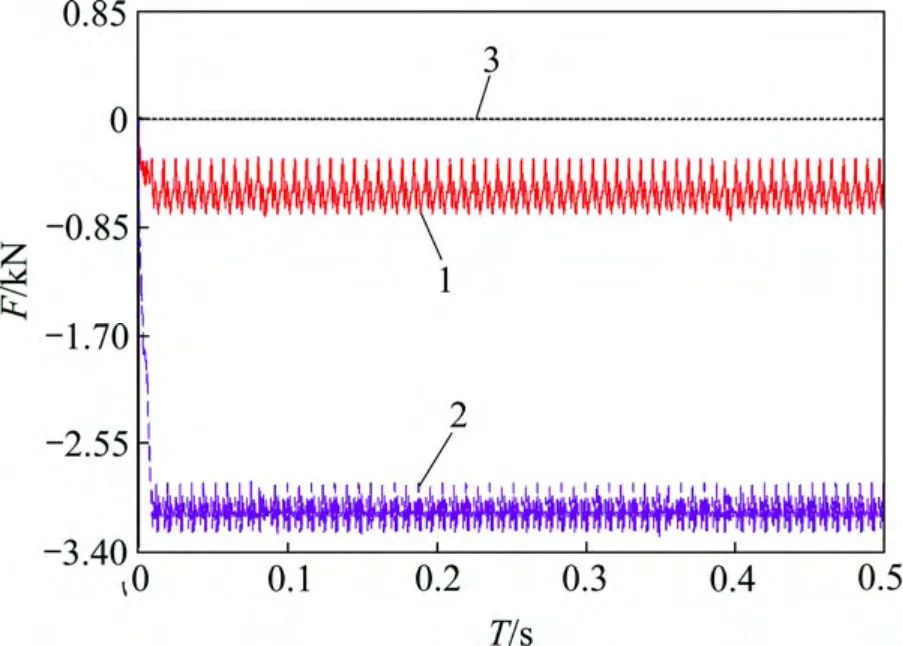
图9 高重合度齿轮啮合力曲线Fig.9 Meshing force of high contact ratio gear

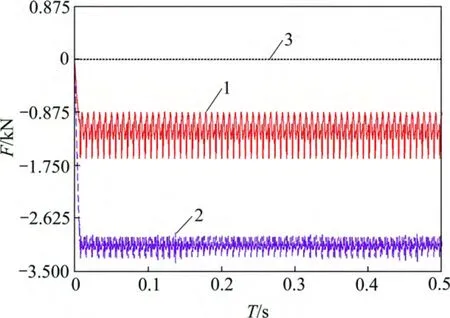
图10 渐开线齿轮啮合力曲线Fig.10 Meshing force of involite gear

1) 与渐开线齿轮传动相同，在仿真开始的瞬间，齿轮突然加速，啮合力随齿轮啮合的进行发生波动，但波峰间距较大，即齿轮啮合周期较长，随着传动的进行，啮合力在一个均值附近以一定的幅值和周期上下波动，周期和幅值趋于稳定，这是齿轮周期性啮入啮出冲击的表现。

2) 渐开线齿轮传动的径向啮合力在均值处的波动幅值为758.43 N，而高重合度齿轮传动的径向啮合力在均值处的波动幅值为459.16 N，比渐开线齿轮传动减少了39.5%。

3) 渐开线齿轮传动的切向啮合力在均值处的波动幅值为399.24 N，而高重合度齿轮传动的切向啮合力在均值处的波动幅值为351.05 N，比渐开线齿轮传动减小了12.1%。因此，从仿真结果来看，高重合度齿轮传动的啮入啮出冲击相对较小，传动更加平稳。

6 结论

1) 利用基于压力角的齿轮主动设计方法，可以在设计之前就预知齿轮传动的重合度，还可以直接计算其曲率、滑动系数等啮合特性，为方便快捷地设计满足不同重合度需求的特殊齿轮奠定了基础。

2) 与相同参数的渐开线齿轮相比，利用本文提出的方法设计的重合度为3 的齿轮，具有最大接触应力小，滑动系数小的优点，有利于改善齿轮的磨损状况，提高齿轮寿命。

3) 在相同条件下，高重合度齿轮传动的径向啮合力在均值处的波动幅值比渐开线齿轮减少了39.5%，切向啮合力在均值处的波动幅值比渐开线齿轮减小了12.1%，因此，其啮入啮出冲击和传动的平稳性均优于渐开线齿轮。

[1] Tsai M H,Tsai Y C.Design of high-contact-ratio spur gear using quadratic parametric tooth profiles[J]. Mechanism and Machine Theory,1998,33(5):551-564.

[2] TAN Weiming. Common definition for end-surface contact ratio of gears and its applications[J]. Chinese Journal of Mechanical Engineering,2004,17(4):595-597.

[3] LI Shuting. Effect of addendum on contact strength, bending strength and basic performance parameters of a pair of spur gears[J]. Mechanism and Machine Theory, 2008, 43(12):1557-1584.

[4] 尹刚. 高重合度齿轮应力场有限元分析[J]. 重庆大学学报(自然科学版),2010,33(7):53-57.YIN Gang. Finite element analysis of high contact-ratio gear stress field[J].Journal of Chongqing University (Natural Science Edition),2010,33(7):53-57.

[5] 邓效忠, 方宗德, 魏冰阳, 等. 高重合度弧齿锥齿轮加工参数设计与重合度测定[J]. 机械工程学报,2004,40(6):95-99.DENG Xiaozhong, FANG Zongde,WEI Bingyang,et al.Design and experiment of spiral bevel gears with high contact ratio[J].Chinese Journal of Mechanical Engineering,2004,40(6):95-99.

[6] 王三民, 纪名刚. 高速大重合度直齿圆柱齿轮的齿廓最佳修形研究[J]. 航空学报,1996,17(1):121-124.WANG Sanmin, JI Minggang. Study on the best profile modification of high-speed spur gears with high-contact-ratio[J].Acta Aeronautica et Astronautica Sinica,1996,17(1):121-124.

[7] 渠珍珍, 杨杭旭. 高重合度齿轮的实现方法及其参数设计[J].机电技术,2012(3):103-105.QU Zhenzhen,YANG Hangxu.Realization and parameter design of high contact ratio gears[J]. Mechanical & Electrical Technology,2012(3):103-105.

[8] 林菁. 基于啮合角函数的平面圆齿轮共轭齿廓求解及几何特性研究[J]. 机械传动,2004,28(3):6-8.LIN Jing. A direct-profile-design method for generating noncircular gear pairs[J]. Journal of Mechanical Transmission,2004,28(3):6-8.

[9] Yeh T, Yang D C H, Tong S H, Design of new tooth profile for high-load capacity gears[J]. Mechanism and Machine Theory,2001,36(10):1105-1120.

[10] Pedrero J I, Artés M, García-Prada J C. Determination of the addendum modification factors for gears with pre-established contact ratio[J]. Mechanism and Machine Theory, 1996, 31(7):937-945.

[11] WANG Jian, HOU Liang, LUO Shanming, et al. Active design of tooth profiles using parabolic curve as the line of action[J].Mechanism and Machine Theory,2013,61(9):47-63.

[12] 孟兆明, 许基琴, 汪惠琴. 渐开线齿轮点蚀位置的确定及其计算综合曲率半径的误差修正[J]. 青岛科技大学学报,2004,25(4):339-342.MENG Zhaoming, XU Jiqin,WANG Huiqin.The definition and calculation of the location of spot erosion for involute gear correction of the errors for the composite curve radius[J].Journal of Qingdao University of Science and Technology, 2004, 25(4):339-342.

[13] 刘令涛, 焦永和, 张春林, 等. 内平动全摆线齿轮曲率半径的分析[J]. 北京理工大学学报,2010,30(2):158-160,173.LIU Lingtao, JIAO Yonghe, ZHANG Chunlin, et al. Analysis of the curvature radius of internal parallel moving gears with whole cycloidal profiles[J]. Journal of Beijing Institute of Technology,2010,30(2):158-160,173.

[14] 林菁. 共轭曲线啮合角函数理论及其应用[M]. 北京: 科学出版社,2005:31-35.LIN Jing. Theory and application of working pressure angle function for conjugate curves[M]. Beijing: Science Press, 2005:31-35.

[15] 李三群, 贾长治, 武彩岗, 等. 基于虚拟样机技术的齿轮啮合动力学仿真研究[J]. 系统仿真学报,2007,19(4):901-904.LI Sanqun, JIA Changzhi, WU Caigang, et al. Dynamic simulation study of gear meshing based on virtual prototyping technology[J]. Journal of System Simulation, 2007, 19(4):901-904.