一种新型煤灰分双能量γ 射线检测方法

程栋，滕召胜，黎福海，代扬

(湖南大学 电气与信息工程学院，湖南 长沙，410082)

煤炭在我国的能量供给体系中占有非常重要的地位，提高煤炭的利用效率对发展我国的国民经济意义重大。煤灰分即煤灰成分(质量分数)是衡量煤炭的主要经济指标，煤灰分与发热量也密切相关，对于火力发电厂、选煤厂、煤矿、炼焦厂、水泥厂、化肥厂、钢铁厂等这些大型的用煤单位来说，煤灰分的检测具有重大意义[1]。与传统的化验方法相比，利用辐射测量技术则能够实现煤灰分的快速检测，解决了传统方法的采样、制样、化验工序复杂问题，规避了结果滞后时间长所带来的一系列问题，还能够大大减轻工人劳动强度，并且检测结果的客观性较好[2]。具有代表性的辐射型煤灰分检测方法有低能γ 射线反散射法、高能γ 湮没辐射法、天然γ 放射性煤灰分测量法、双能量γ 射线透射法和中子瞬发γ 分析法[3]。低耗γ 射线反散射法对煤的几何条件要求很严格，即要求被测煤的粒度小，煤流表面平整，煤流的密实度应保持稳定，煤层与探测器表面之间的距离应保持不变，煤层厚度应保持大于饱和厚度等，因此，该方法难以实现真正的在线测量[4]。高能γ 湮没辐射法中，高能射线穿透能力强，屏蔽困难，辐射安全性差，而且同时对灰分的测量灵敏度较低，不能得到广泛应用[5]。天然γ放射性的煤灰分测量法通过测量由煤的天然放射性引起的γ 计数率确定煤灰分，但对含量只有百万分之几的天然放射性引起的γ 计数率的准确测量是非常困难的[6]。中子瞬发γ 分析法通过分析、测量中子与煤中各种元素的非弹性散射和俘获辐射产生的瞬发γ 射线对煤灰分进行检测，但在目前已有的此类设备中，使用的放射源为252Cf，其半衰期只有2.5 a，频繁更换放射源不但花费大而且很繁琐，故并未广泛应用[7]。双能量γ 射线透射法与其他方法相比较，测量精度高，受物料的形状、厚度、粒度、堆密度等因素影响小，而且性价比高，为此，本文作者对双能量γ 射线透射法煤灰分检测算法进行改进[8]。不同的煤中各种原子序数元素的相对含量不同，因此，在实际检测灰分前，必须进行现场标定。针对传统的数值逼近标定方法所带来的实际误差较大的问题[9-10]，提出基于模糊最小二乘支持向量机的标定方法。支持向量机(support vector machine，SVM)是一种新型的学习方法，通过结构风险最小化原理提高泛化能力，较好地解决了小样本、非线性、高维数、局部极小点等问题，广泛应用于模式识别、信号处理和时间序列预测等领域[11]。最小二乘支持向量机(least squares support vector machine, LSSVM)是支持向量机的一种扩展，优化指标采用平方项，并用等式约束代替标准支持向量机的不等式约束，将二次规划问题转化为求解线性方程组，降低了计算复杂性，从而提高了求解速度[12]。LSSVM建模中必须设定正则化参数g 和核函数宽度δ 这2 个参数。g 是最小化训练误差和最小化模型复杂度之间的折中，对LSSVM 模型的推广性能有重要影响，而δ 是直接影响支持向量数目的参数，若δ 较小，则产生大量的支持向量，最终导致过饱和，而若δ 较大，则使支持向量减少，使模型更加简化，最终导致模型精确度降低，因此，存在着g 和δ 的优化问题。为提高煤灰分的LSSVM 预测精度，采用混沌方法优化的g 和δ 参数[13-14]。

1 煤灰分检测原理

1.1 γ 射线和煤灰分的相互作用原理

γ 射线与煤灰分的相互作用主要有3 类过程：光电效应、康普顿效应和电子对产生[15]。当1 个γ 光子与煤灰分原子中的束缚电子作用时，光子把全部能量交给这个电子，使它脱离原子的束缚而发射出去，而光子本身消失，这种过程称为光电效应。康普顿效应是光子与核外电子发生非弹性碰撞，γ 光子把部分能量转移给电子使其从原子内部反冲出来，而能量降低了的光子沿着与原来运动方向不同的角度散射出去。当入射光子的能量大于1.02 MeV 时，有可能在原子核附近转化为1 个正电子和1 个负电子，γ 光子本身消失，这种过程称为电子对产生。

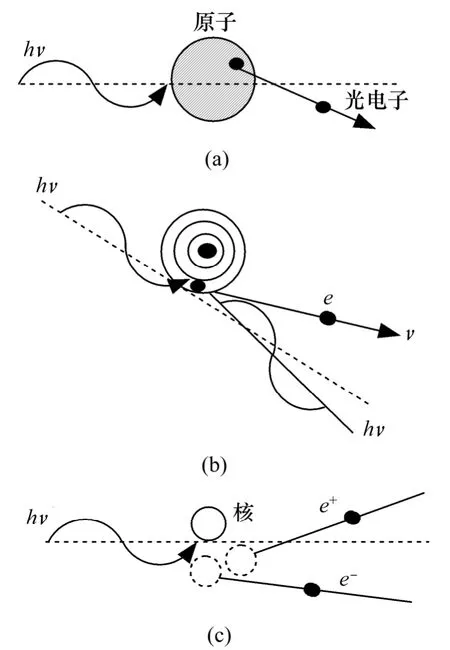
图1 γ 射线和煤灰分作用示意图Fig.1 Schematic diagram of interaction between γ-ray and ash of coal

1.2 γ 射线透射煤灰分的衰减规律

假设有一平行光子束垂直入射到煤灰分的表面上，在每平方厘米面积上每秒的光子数目为I，吸收煤灰分单位体积内的原子数目为N，当光子束穿过厚度为dx 的吸收煤灰分时，发生互相作用的光子数为dI，则有

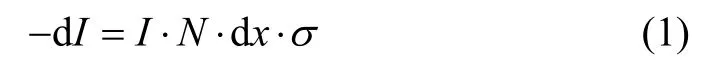
式中：σ 为比例常数；Ndx 为厚度dx 内单位面积上的原子数目。由式(1)可知

式中：I0为单位时间内入射到垂直于γ 光子束单位面积煤灰分上的γ 光子数目；I 为单位时间内穿透厚度为x 的煤灰分后垂直于γ 光子方向单位面积煤灰分上的γ光子数目；N 为单位面积煤灰分上的原子数目；x 为吸收煤灰分的厚度；σ 为每个原子对γ 光子的作用截面。令

则式(2)可改写为

式中：μ 为煤灰分对γ 射线的线衰减系数。

1.3 双能量γ 射线透射法检测模型

在双能量γ 射线透射法中，其中一种射线是低能γ 射线，另一种射线是中能γ 射线。当2 种γ 射线以同一准直射束穿过煤样时，将按窄束射线透射物质时的指数规律进行衰减。其中低能γ 射线的衰减规律为

式中：I0和I 分别为无煤时和煤层吸收后探测器测试到的一定时间间隔内的低能γ 计数，与其通量密度成正比；μL(低)为煤对γ 射线的质量衰减系数；ρ 为煤的堆积密度；d 为煤的厚度；ρd 为被透射煤的质量厚度。由式(5)可得：

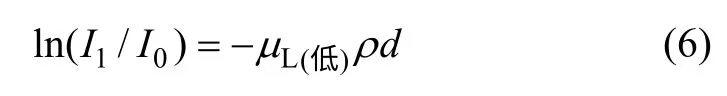
煤看作是2 种原子序数元素的混合物：一种是以C 为代表的原子序数比较低的元素，简称为低Z 元素；另一种物质是以Si 和Al 为代表的原子序数比较高的元素，简称为高Z 元素。假设被测煤中高Z 元素的质量分数为CZ，则低Z 元素所占质量分数为(1-CZ)，按照量衰减系数的计算规律，煤对低能γ 射线的质量衰减系数为

将式(7)代入(6)得

同理，对于中能射线，有

式中：J0和J 分别为无煤时和煤层吸收后探测器测试到的γ 计数； μZ(低)为煤中高Z 元素对低能射线的质量衰减系数； μC(低)为煤中低Z 元素对低能射线的质量衰减系数； μZ(中)为煤中高Z 元素对中能射线的质量衰减系数； μC(中))为煤中低Z 元素对中能射线的质量衰减系数。因为2 种γ 射线透射过的是同一煤层，式(8)和(9)中煤的质量厚度ρd 是同一量。对于中能γ射线，可以近似地认为高Z 元素质量吸收系数 μC(中)与低Z 元素的质量吸收系数 μZ(中)相等，则有

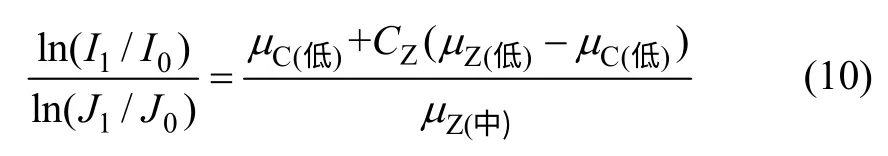
因 为μ C( 低)，μZ(低)和μZ(中)是 常 数， 令ln( I1/ I0)/ln( J1/ J0)= R，则整理式(10)得

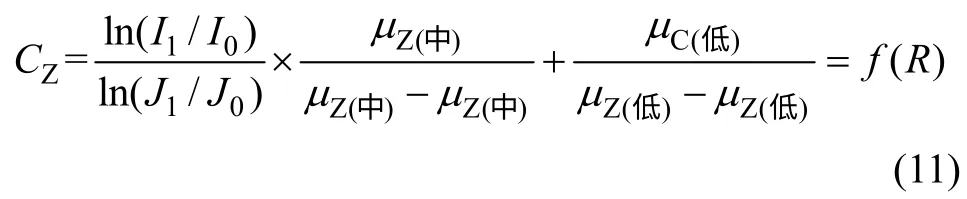
因为煤的灰分可被近似认为测定煤样中高Z 元素的质量元素的2 倍，因此，煤的灰分为A≈2CZ。

1.4 基于混沌最小二乘支持向量机的煤灰分预测

式中：非线性映射Ф：Rm→RN将输入数据映射到一个高维特征空间H；ω∈RN，为权向量；b∈R，为偏差。为了求出x 和y 的函数关系，定义如下优化问题：

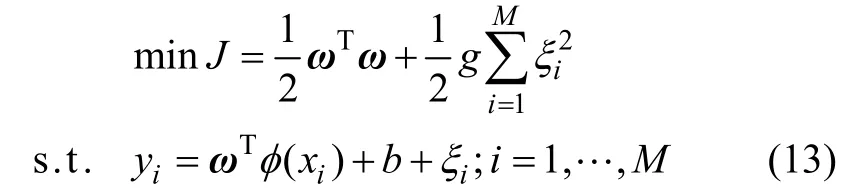
式中：g 为正则化参数；ξi为松弛变量。定义拉格朗日函数为

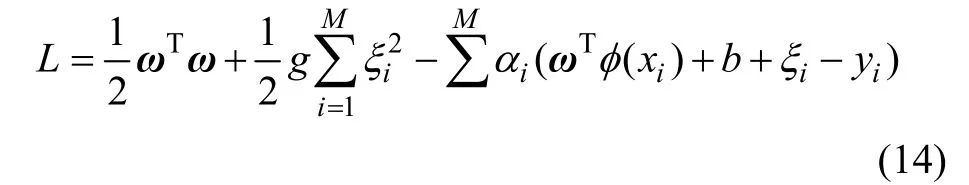
式中：αi为拉格朗日乘子。根据KKT 条件，有

消去ω 和ξi，则式(12)可重写为

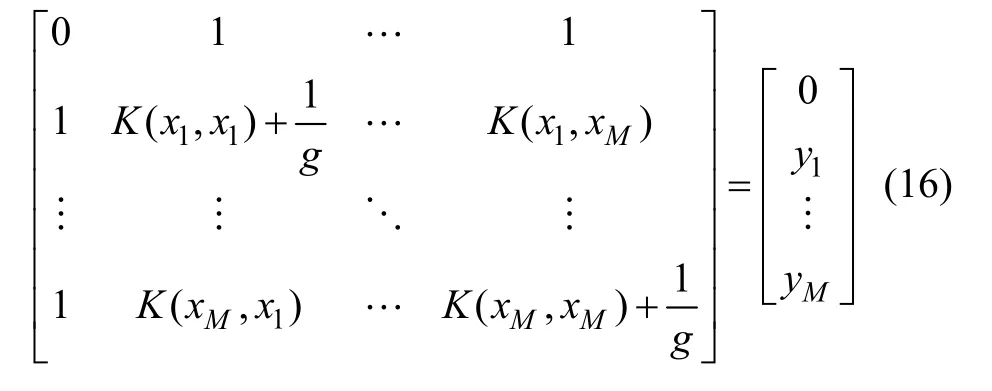
式中：K(·, ·)为核函数，满足

(·)表示H 的内积。解矩阵方程(16)，求得αi和b，最终得到LSSVM 的模型预测输出：

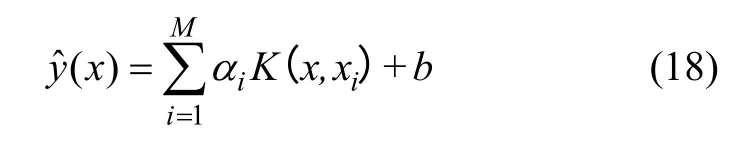
式中：核函数K(x, xi)在本文中采用RBF 核函数，即

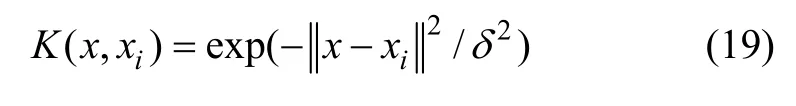
δ 为核函数宽度。

LSSVM 算法中必须优化正则化参数g 和核函数宽度δ 这2 个参数，即

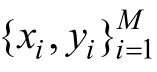
Step 2 采用Logistic 映射产生混沌变量，即

Step 3 将混沌变量映射到可行域：

2.报表填报不规范问题。一是建议加强教育主管部门与财政部门、财政业务部门与预算编审部门之间沟通，以便在预算下达时就能保持口径一致，避免高校财务人员凭职业判断来填报。二是建议主管部门每年编制完决算报表后，组织编报者进行学习总结，指出不规范的地方及其原因，防止在下一年度会计核算中重复出错。三是建议建立决算报表员交流平台，就如何提高决算报表质量、报表数据分析应用等相关情况展开经验讨论，有利于统一和提升业务能力、操作技能。

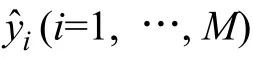
Step 6 n1=n1+1。若n1＜A1，则转向步骤2。

Step 7 返回最优参数g*和δ*以及它们对应的αi和b。

2 实验验证

图2 所示为双能量γ 射线煤灰分检测实验结构框图。实验中包含了1 个γ 射线NaI 探测器，可将微弱的γ 射线通过光电倍增管将其转变为脉冲信号，进而实现γ 射线的计数。在保持合适的放射源强度和半衰期的原则下，选用241Am 作为低能γ 源，137Cs 作为中能γ 源，241Am 和的137Cs 半衰期分别长达485 a 和30 a，并且容易获得。信号处理模块实现了基线恢复、多道分析和区分γ 射线产生的不同幅度的脉冲信号。通过以上模块工程的组合，可实现煤灰分检测中R 的计算。将R 和灰分值分别作为混沌最小支持向量机模块(Chaos-LSSVM)的输入和输出，实现煤灰分的预测。

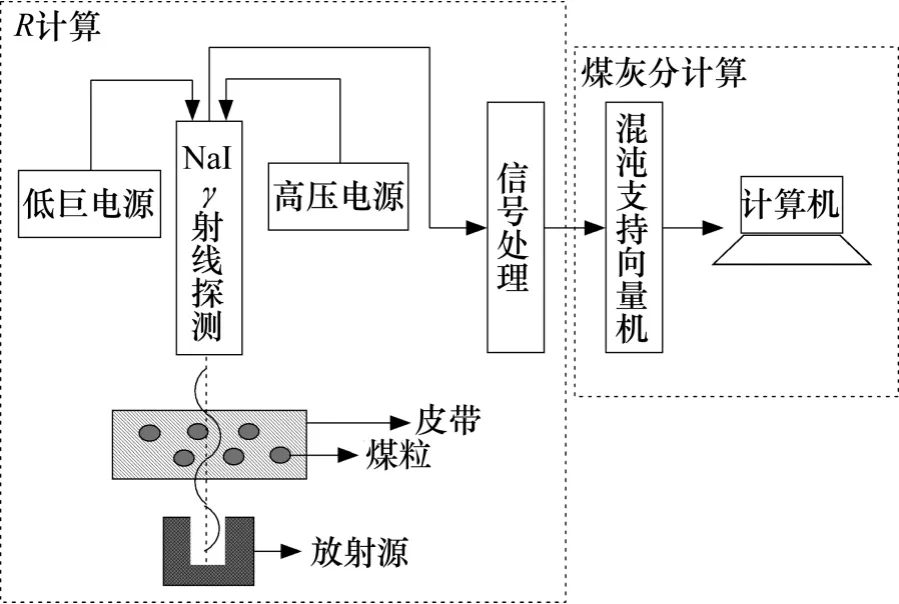
图2 双能量γ 射线煤灰分检测实验系统结构框图Fig.2 Experiment structure diagram of ash determination of coal with dual-energy γ-ray

为验证算法的优越性，采用本文方法与传统方法(直线逼近、最小二乘逼近)对煤灰分检测精度进行对比。实验中的样本为山西某矿的煤颗粒，对其进行多处煤源检测，利用双能量γ 射线进行R 测量，利用燃烧化学方法测量煤灰分真实值，如表1 所示。

图3 和图4 所示为直线逼近和最小二乘逼近对于煤灰分的检测过程。直线与最小二乘逼近方程分别为：A=85.164 8R-122.155 2 和A=24.144 1R2-29.757 6R-10.955 0，其中A 为灰分值。从图3 和图4 可以看出拟合度不是很高，误差偏大。其原因是：除了在测量过程中煤灰分范围变化比较大这一主要原因外，水分的变化、传统化验方法引起的误差、煤样品颗粒度等因素都会产生误差。从图3 和图4 可知灰分随R 的变化关系不一定呈直线关系或二次曲线函数关系，因此，需要调整灰分计算方程，使其能够及时跟踪煤灰分变化。为了解决这一问题，本文利用Chaos-LSSVM 预测煤灰分。

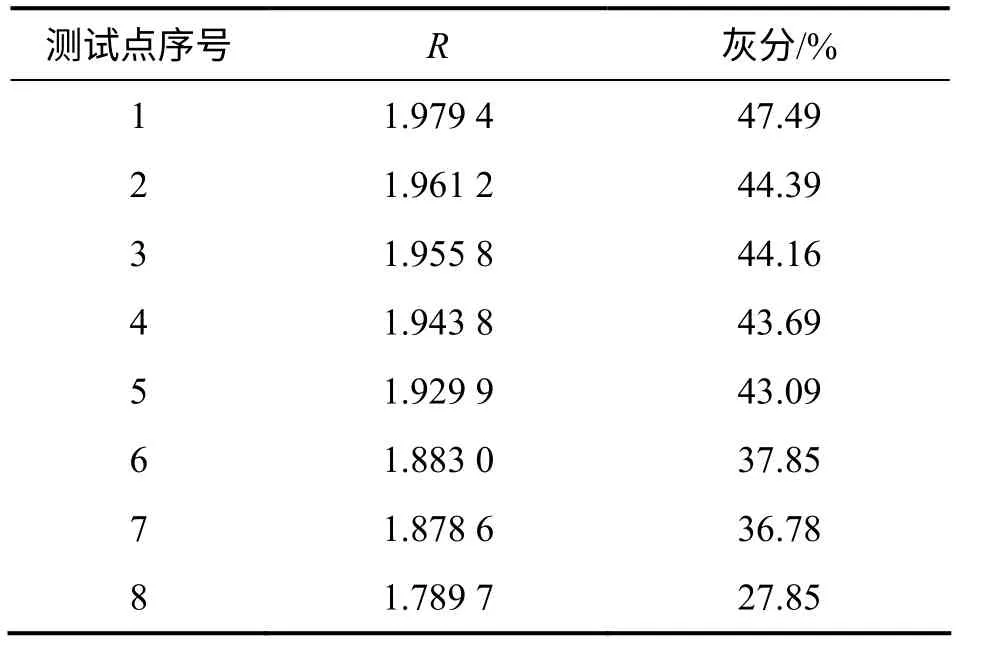
表1 山西某矿煤粒样本值Table 1 R and ash content of coal samples in Shanxi

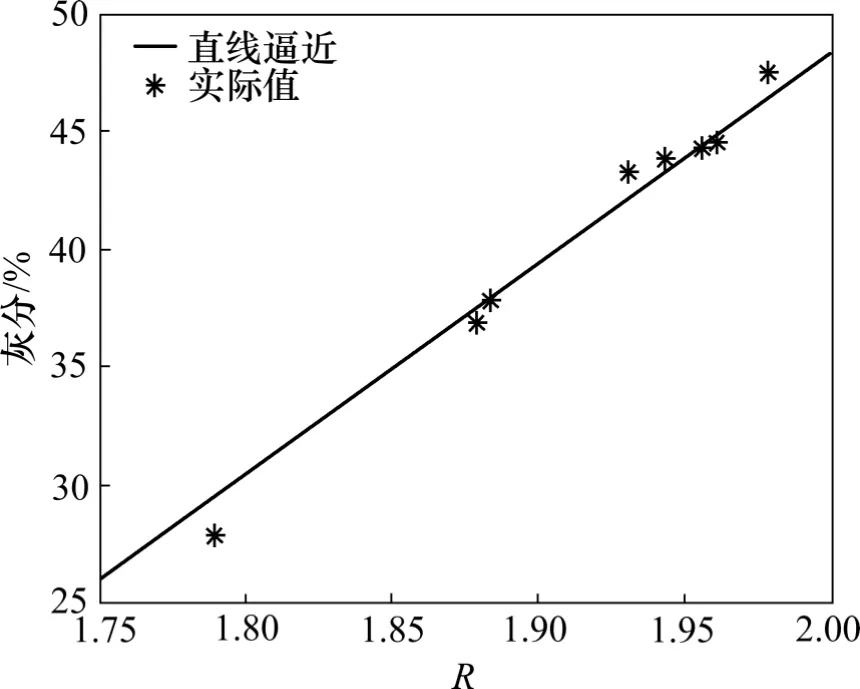
图3 直线逼近算法煤灰分检测过程Fig.3 Ash determination of coal by line approaching

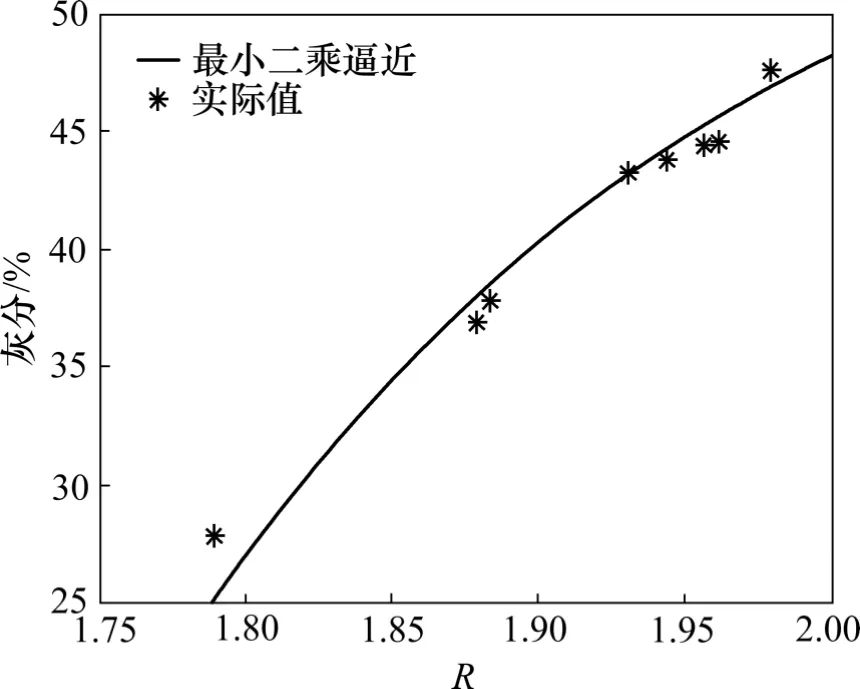
图4 最小二乘逼近算法煤灰分检测过程Fig.4 Ash determination of coal by least squares approaching

为了利用Chaos-LSSVM 预测煤灰分值，选取30份煤粒样本作为Chaos-LSSVM 的训练集，其目标函数为

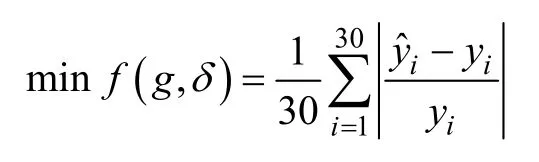
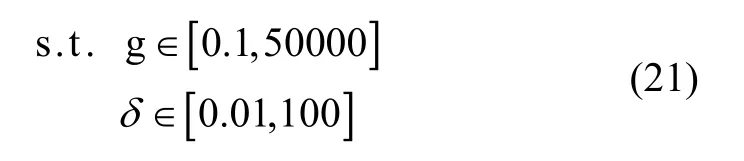
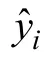
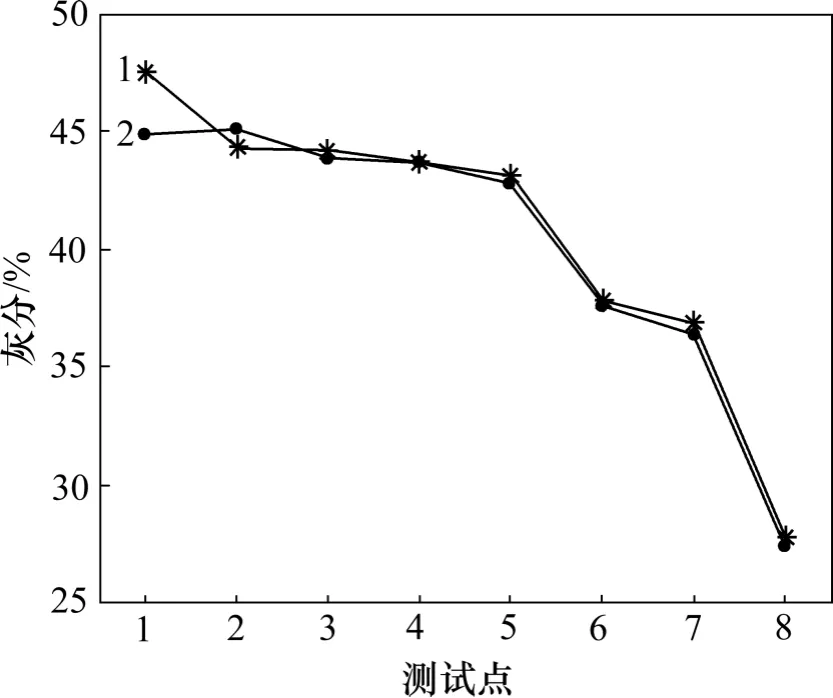
图5 Chaos-LSSVM 灰分预测值与真实值对比Fig.5 Comparison between prediction value and real value of ash

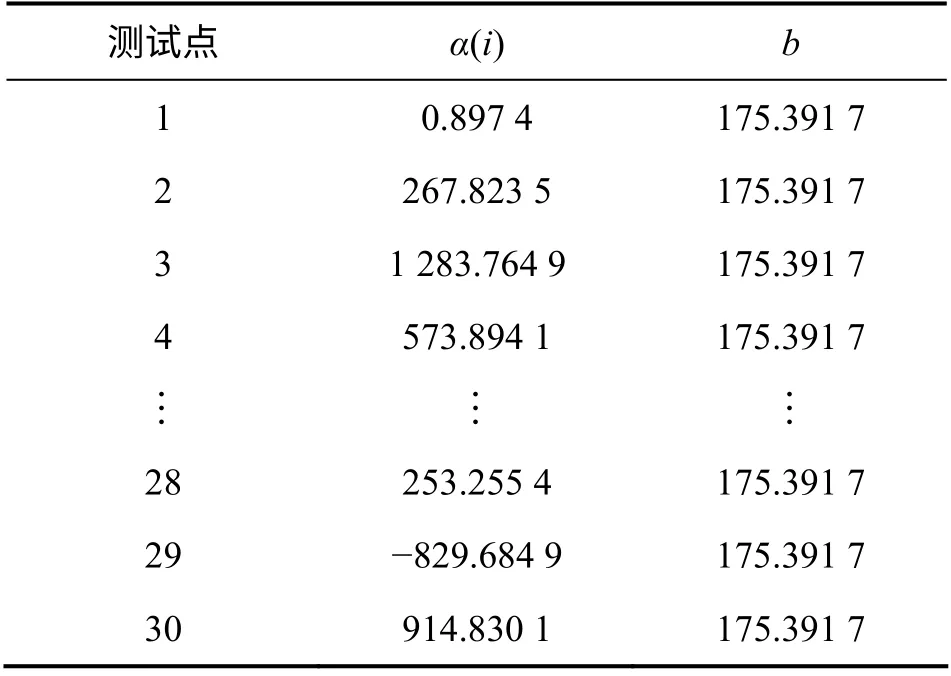
表2 Chaos 优化参数g 和δ 过程中α(i)和b 取值Table 2 Value of α(i) and b in the process of g and δ optimized by Chaos

图6 所示为3 种算法煤灰分检测值与的真实值的相对误差。从图6 可以看出：混沌最小二乘支持向量机的平均相对误差可达到0.8%，表明检测精度较高，并且相对误差较稳定；而直线逼近和最小二乘逼近算法的平均相对误差分别达2.22%和3.19%。

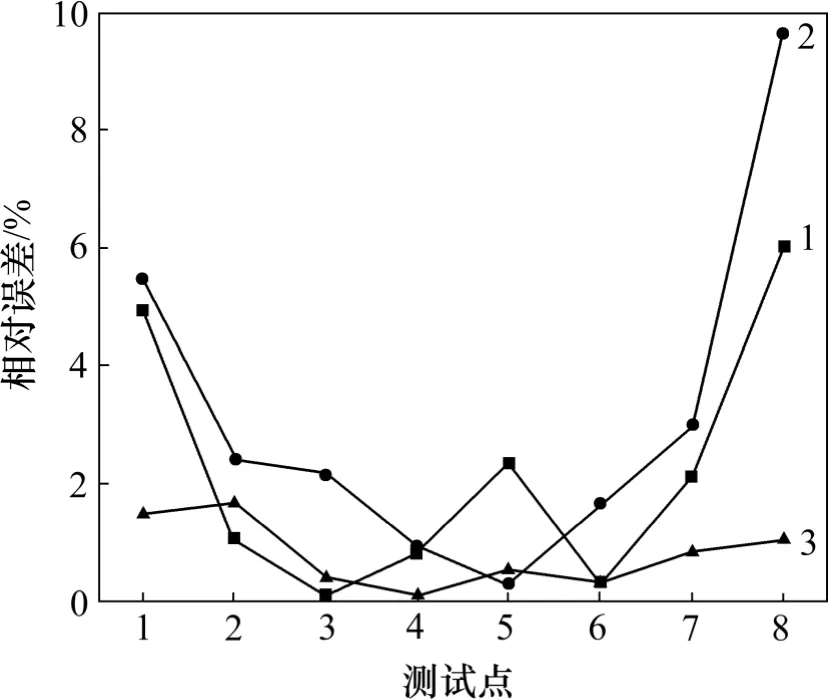
图6 3 种算法煤灰分检测相对误差Fig.6 Relative error of ash determination of coal calculated by three algorithms

3 结论

(1) 针对传统方法对煤灰分检测误差大的问题，提出了基于的煤灰分双能量γ 射线检测方法。该算法通过利用双能量γ 射线透射法和Chaos-LSSVM 可减小煤炭形状、厚度、粒度、堆密度等因素和标定方法引入的误差。

(2) 将241Am 和137Cs 作为低能和中能γ 射线源进行实验验证，在煤灰分检测中平均相对误差为0.8%，与直线逼近和最小二乘逼近算的平均相对误差2.22%和3.19%相比，基于的煤灰分双能量γ 射线检测方法的煤灰分检测精度较高。

[1] 杨华玉. γ 射线在线灰分分析仪的操作测量性能评价方法[J].煤质技术, 2007(3): 31-33.YANG Huayu. Evaluation method for measuring performance of γ-ray ash content apparatus[J]. Coal Quality Technology,2007(3): 31-33.

[2] Borsaru M, Charbucinski J, Rojc A, et al. Probe for determination of ash in coal stockpiles[J]. Nuclear Instruments and Methods in Physics Research B, 2004, 213: 422-425.

[3] Nezamzadeh M, Alavi S H, Lamehi-rachti M, et al. Comparison between (n±γ), (γ±γ) and natural γ-ray activity techniques for ash measurement of coal samples[J]. Applied Radiation and Isotopes,1999, 50(4): 685-691.

[4] 黄兴滨, 王国荣, 孙普男, 等. 测量煤炭灰分的低能γ 射线反散射方法[J]. 核技术, 2005, 28(11): 877-880.HUANG Xingbin, WANG Guorong, SUN Punan, et al.Backscattering techniques of low energy γ-ray for determining ash content of coal[J]. Nuclear Technology, 2005, 28(11):877-880.

[5] 衣宏昌, 粱漫春, 林谦. 基于辐射测量技术的几种煤灰分检测方法的比较[J]. 选煤技术, 2004(2): 54-56.YI Hongchang, LIANG Manchun, LIN Qian. Comparison of several ash monitoring methods relying on radiation measuring technology[J]. Coal Preparation Technology, 2004(2): 54-56.

[6] Rizk R A M, EI-kateb A H, Abdul-kader A M. On-line nuclear ash gauge for coal based on gamma-ray transmission techniques[J]. Journal of Radioanalytical and Nuclear Chemistry,1999, 242(1): 139-145.

[7] Lim C S, Abernethy D A. On-line coal analysis using fast neutron-induced γ-ray[J]. Applied Radiation and Isotopes, 2005,63(5): 697-704.

[8] Asfahani J. Optimization of low activity spectrometric gammagamma probes for ash determination in coal stockpiles[J].Applied Radiation and Isotopes, 2003, 58(6): 643-649.

[9] 许燕, 张国生. 加权最小二乘法在煤灰分模型中的应用[J].北京印刷学院学报, 2010, 18(2): 68-69.XU Yan, ZHANG Guosheng. Application of weighted least square method in the coal ash model[J]. Journal of Beijing Institute of Graphic Communication, 2010, 18(2): 68-69.

[10] Sang H F, Wang F L, Liu L M, et al. Detection of element content in coal by pulsed neutron method based on an optimized back-propagation neural network[J]. Nuclear Instruments and Methods in Physics Research B, 2005, 239(3): 202-208.

[11] Tao S H, Chen D X, Zhao W X. Fast pruning algorithm for multi-output LS-SVM and its application in chemical pattern classification[J]. Chemometrics and Intelligent Laboratory Systems, 2009, 96(1): 63-69.

[12] Wang Y H, Zhao X Y, Wang B T. LS-SVM and Monte Carlo methods based reliability analysis for settlement of soft clayey foundation[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2013, 5(4): 312-317.

[13] Hu Y X, Zhang H T. Chaos optimization method of SVM parameters selection for chaotic time series forecasting[C]//Physics. Procedia, 2012: 588-594.

[14] Wang Y, Guo W. Local prediction of the chaotic fh-code based on LS-SVM[J]. Journal of Systems Engineering and Electronics,2008, 19(1): 65-70.

[15] Borsaru M, Dixon R, Rojc A. Coal face and stockpile ash analyser for the coal mining industry[J]. Applied Radiation and Isotopes, 2001, 55(3): 407-412.