Highly Biased Hygroscopicity Derived from Size-Resolved Cloud Condensation Nuclei Activation Ratios without Data Inversion

DENG Zhao-Ze and RAN Liang

Key Laboratory of Middle Atmosphere and Global Environment Observation, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China

Highly Biased Hygroscopicity Derived from Size-Resolved Cloud Condensation Nuclei Activation Ratios without Data Inversion

DENG Zhao-Ze and RAN Liang

Key Laboratory of Middle Atmosphere and Global Environment Observation, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029, China

The impact of aerosols on the climate and atmospheric environment depends on the water uptake ability of particles; namely, hygroscopic growth and activation into cloud condensation nuclei (CCN). The size-resolved activation ratios (SRAR), characterizing the fraction of aerosol particles that act as CCN at different particle sizes and supersaturations, can be measured using a combination of differential mobility analyzers (DMA) and particle counters. DMA-based measurements are influenced by the multiply charged particles and the quasi-mono-dispersed particles (effect of DMA transfer function) selected for each prescribed particle size. A theoretical study, assuming different particle number size distributions and hygroscopicity of aerosols, is performed to study the effects of the DMA transfer function and multiple charging on the measured SRAR and the derived hygroscopicity. Results show that the raw SRAR can be significantly skewed and hygroscopicity may be highly biased from the true value if the data are not corrected. The effect of the transfer function is relatively small and depends on the sample to sheath flow ratio. Multiply charged particles, however, can lead to large biases of the SRAR. These results emphasize that the inversion algorithm, which is used to correct the effects of the DMA transfer function and multiple charging, is necessary for accurate measurement of the SRAR.

cloud condensation nuclei, size-resolved activation ratio, data inversion

1 Introduction

Atmospheric aerosols have a direct effect on climate and environment by altering the budget of radiation and an indirect effect by changing the properties of clouds. Both the direct and indirect effects of aerosols depend not only on their population and dry sizes, but also on their water uptake ability. When exposed to humidified air, particles grow in size, and hence scatter more light and degrade the visibility. At sufficient supersaturations, a fraction of aerosol particleswill be activated as cloud condensation nuclei (CCN) and form cloud droplets. Particles with larger hygroscopicity can grow to a larger size in a subsaturated condition and be activated as CCN at lower supersaturations.

A great many studies have been carried out to measure the hygroscopicity of aerosols using different approaches. Humidified tandem differential mobility analyzers (H-TDMA) have been used to measure diameter growth factors at a maintained relative humidity (Swietlicki et al., 2008; Massling et al., 2009; Meier et al., 2009; Liu et al., 2011). Scattering growth factors of bulk aerosols have been measured using humidified nephelometers (Pan et al., 2009) or visibility meters (Li et al., 2013). Hygroscopic parameters can also be determined from measurements of the aerosol chemical composition (Liu et al., 2014).

In recent years, size-resolved activation ratios (SRAR) (Frank et al., 2006), which can be used to characterize aerosol hygroscopicity in supersaturated conditions, have been measured using a combination of differential/ scanning mobility particle sizers (DMPS/SMPS) (Wang et al., 2003; Wiedensohler et al., 2012) and CCN counters (CCNC) (Roberts and Nenes, 2005; Lance et al., 2006). This method was applied to calibrate the CCNC (Rose et al., 2008), and also to measurements made in the laboratory (Cruz and Pandis, 1997) and in field campaigns (Dusek et al., 2006; Rose et al., 2010; Deng et al., 2011; Gunthe et al., 2011). The SRAR, which provides the information on both the size-resolved chemical compositions and the mixing states of aerosols, was used to reasonably predict the CCN number concentrations in closure studies (Deng et al., 2013). The diameter where 50% of the particles are activated (D50) is commonly referred to as the critical dry diameter and is used to calculate hygroscopicity parameters.

However, SRAR requires data inversion, since the measurements employ a differential mobility analyzer (DMA) to separate mono-dispersed aerosol particles from the poly-dispersed ones. There are two effects: 1) rather than selecting only one single particle size (electrical mobility) the DMA selects a range of particle sizes (DMA transfer function); 2) rather than selecting only particles with a prescribed size and a single charge the DMA also selects some larger ones carrying multiple charges with the same electrical mobility. Both the DMA transfer function width and the multiple charging skew the measured SRAR. Petters et al. (2007) found that multiply charged particles might lead to a non-monotonic SRAR if themode diameter of the particle number size distribution (PNSD) exceeds the critical dry diameter and the estimated D50 by minimizing theχ2-statistic defined therein. Rose et al. (2008) corrected for multiply charged particles by assuming a constant multiply charged fraction across the whole size range, and characterized SRAR as a two-step function. Frank et al. (2006), Moore et al. (2010), and Deng et al. (2012) presented different methods for full inversion algorithms, which are used to correct the effects of the DMA transfer function and multiple charging.

During several measurement campaigns in the North China Plain, the inverted SRAR differ largely from the raw data, which usually overestimate the activation ratios around the critical diameters. In this work, the highly biased hygroscopicity parameters derived from the raw SRAR are presented via a theoretical study to emphasize the importance of data inversion.

2 Methodology

To estimate the potential deviation induced by lack of data inversion, we perform a forward numerical calculation of the measured quantities using assumed aerosol properties and instrument settings.

2.1 Assumption of particle number size distribution and hygroscopicity

The PNSD of atmospheric aerosols can be roughly represented by a logarithmic normal distribution, i.e.,

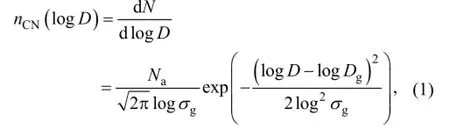
whereDis the diameter of aerosol particles. The aerosol number concentration,Na, is assumed to be constant (20000 cm3), sinceNadoes not influence the calculation of activation ratios. Here, the geometric deviation,gσ, is set as 1.5-2.0 (Wu et al., 2008; Shen et al., 2011). The geometric mean diameter,Dg, which usually varies from several to hundreds of nanometers, has a significant influence on the calculated results. Here,Dgis chosen as a set of values between 50 nm and 200 nm, which covers the range of peaks for CCN-active aerosols.

The hygroscopicity of atmospheric aerosols is complicated, because aerosol particles are composed of a large number of substances and these compounds can be internally or externally mixed. Petters and Kreidenweis (2007) proposed a single parameter,κ, to represent the hygroscopicity of aerosols, which avoids a detailed description of chemical compositions and allows measurements and parameterizations of hygroscopicity from different methods to be linked. To simplify the characterization of hygroscopicity, we adapted the size-dependentκfrom Liu et al. (2014) as centralκvalues at the given dry sizes. The SRAR at supersaturation,S, can be expressed as

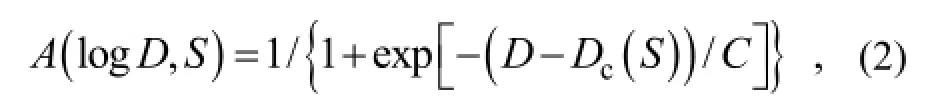
where the critical dry diameter,Dc(S), is determined by the supersaturationS, the temperatureT, and the sizedependentκ. The parameterC, which is zero for aerosols with homogenous chemical compositions, represents the effect of the aerosol-mixing state on hygroscopicity.Cis set asDc(S)/10, which well characterizes the aerosol activation curves according to previous measurements.

The number size distribution of particles serving as CCN (CNSD) at supersaturationScan therefore be expressed as

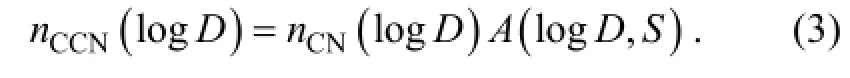
2.2 Measured concentrations in condensation particle counter (CPC) and CCNC

The DMPS/SMPS-CCNC system measures CN and CCN number concentrations, (NCN(D) andNCCN(D,S)), at different sizes and different supersaturations, and thus provides measurements of SRAR,Am(D,S) =NCCN(D,S)/NCN(D). The DMA selects particles with a certain range of electrical mobility. The selected portion of particles from the DMA, however, contains not only particles with specified diameters, but also ones with the same mobility but multiply charged. Both the DMA transfer function width and the multiple charging contribute to skewing the direct measurement of activation ratios. Here, we simulate the concentrations measured in CPC and CCNC following Hagen and Alofs (1983).

The DMA selects particles with mobilityZi(i= 1, 2, …,I) when assigned a diameterDi, and the measured concentration

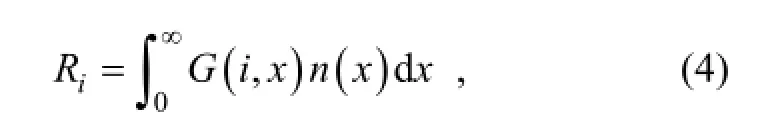
where the size parameterx= logD. The kernal function,G(i,x), is

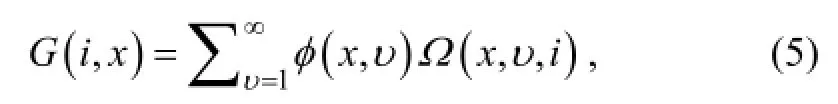
whereφ(x,υ) is the probability that a particle of sizexcarriesυcharges. (Wiedensohler, 1988).Ω(x,υ,i) is the transfer function of the DMA (Knutson and Whitby, 1975), and is related to the sample to sheath flow ratio.

Equation (4) is calculated numerically at intervals much smaller than the measurement, in size range [xint,1,xint,J]. The particle number size distribution at sizexint,jis expressed as a linear interpolation of those at selected sizes,

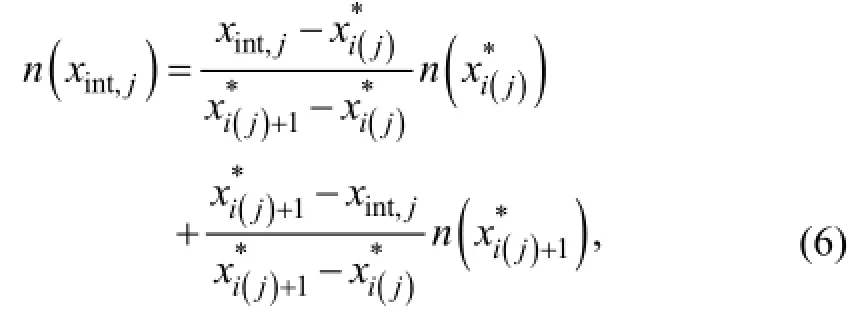
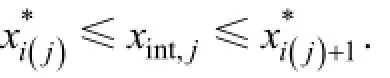
Equation (4) is thereby written as

where

Dirac Function

Let

then Eq. (4) becomes

The equation set-up can be written in matrix form as

whereTis anI×Imatrix determined by the DMA hardware and settings, andRandNare vectors with lengthI. With known number size distribution,, the concentrations measured by CPC and CCNC can be calculated.

3 Results

3.1 An example of biased SRAR

Figure 1 presents an example of the calculated results, assuming PNSD with a geometric mean diameter of 120 nm, a geometric deviation of 1.5, and a critical dry diameter of 70 nm (equivalently,κ= 0.2257 at a supersaturation of 0.4372% and a temperature of 20°C). In this case, the sample to sheath ratio is set as 1:4.

Figure 1a shows the PNSD and corresponding CNSD induced from the assumed SRAR. Using the charging probability of particles and the flow ratio setting in the DMA, the raw concentrations of CN and CCN measured by CPC and CCNC are calculated (Fig. 1b), which provides an estimation of SRAR taking account of the non-zero width of the DMA transfer function width and the multiply charged particles (Fig. 1c). The activationratios are generally higher than the true values. As the activation ratio is larger for larger sizes, the raw activation ratios for a selected particle size are enhanced due to the inclusion of larger particles with the same mobilities and multiple charges. The width of the activation curve is also larger than the true value.

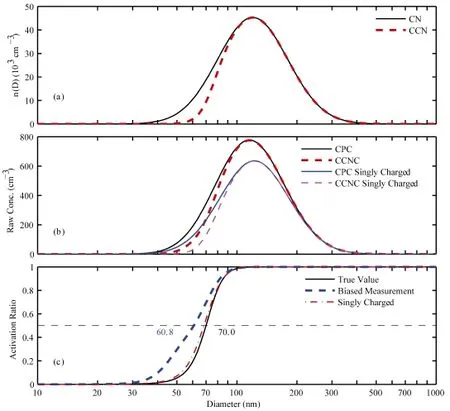
Figure 1 An example of particle/cloud condensation nuclei (CCN) number (a) size distributions, (b) the measured concentrations, and (c) activation ratios.

An activation critical diameter,D50,raw, can be calculated as the diameter where the raw activation ratio is 0.5. In this case,D50,rawis 60.8 nm, while the true value is 70 nm. If the SRAR are not corrected for multiple charging and the DMA transfer function, the derived hygroscopicity is overestimated asκ= 0.3455 at a diameter of 60.8 nm.

3.2 Biased hygroscopicity for PNSDs with different geometric mean diameters

The numerical calculation of the concentrations measured by CPC and CCNC is performed for PNSD with different geometric mean diameters and geometric deviations at different supersaturations. The critical diameters and hygroscopicity are calculated for the SRAR without data inversion (Fig. 2a). Here only the results for the geometric deviation of 1.5 are shown, since the results for other geometric deviations are similar.

The true values of hygroscopicity,κ, are between 0.22 and 0.24 at diameters of 40-120 nm; they slightly increase with diameter, and reach 0.33 at a diameter of 270 nm. Without data inversion, the measured hygroscopicity for PNSDs with a small geometric mean diameter is overestimated at small critical sizes (large supersaturations) and is underestimated at large critical dry sizes (small supersaturations). For PNSDs with large geometric mean diameters, the hygroscopicity is generally overestimated, especially at small critical sizes (large supersaturations). Super-100 nm particles have a high probability of being doubly charged, leading to a large deviation of the calculated hygroscopicity from the true values for PNSDs with large geometric mean diameters.

3.3 Influence of multiply charged particles on the measured hygroscopicity

To quantify the contribution of multiply charged particles to the biases of hygroscopicity, we also perform a calculation considering only the singly charged particles. The thin lines in Fig. 1b present the concentration of singly charged particles measured by CPC and CCNC. The measured number concentrations for particles smaller than 200 nm contain a fraction of multiply charged particles, since super-100 nm particles have a large probability of being multiply charged. The resulting SRARs (Fig. 1c) are not an exact fit but are close to the true values compared to the SRARs with multiply charged particles. The hygroscopicity derived from singly charged particles (Fig. 2b) decreases with diameter between 40 nm and 120 nm, while the true value increases with diameter. The measured hygroscopicity for a singly charged particle is higher for PNSDs with larger geometric mean diameters. However, the measured hygroscopicity for singly charged particles are only slightly different from the true values, less than 0.04, indicating that multiply charged particles account for most of the deviation.

3.4 Influence of DMA sample to sheath flow ratio on the measured hygroscopicity

The width of the DMA transfer function also influences the derived hygroscopicity. The width of the DMA transfer function, which is determined mainly by the DMA sample to sheath flow ratio,Fsa/Fsh, is usually characterized in the range of mobility by a triangle with a height of one-and-a-half times the width ofZiFas/Fshcentered at the prescribed mobility,Zi. The hygroscopicity parameters are recalculated using a narrower DMA transfer function at anFsa/Fshof 1:10. The derived hygroscopicity parameters are also highly biased when multiply charged particles are included (Fig. 3a), although they arecloser to the true values than those using anFsa/Fshof 1:4. The derived hygroscopicity parameters without multiply charged particles are very close to the true values (Fig. 3b), with the largest deviation less than 0.01. A narrower DMA transfer function results in a smaller bias, because the quasi-mono-dispersed particles selected by the DMA have a smaller size range.

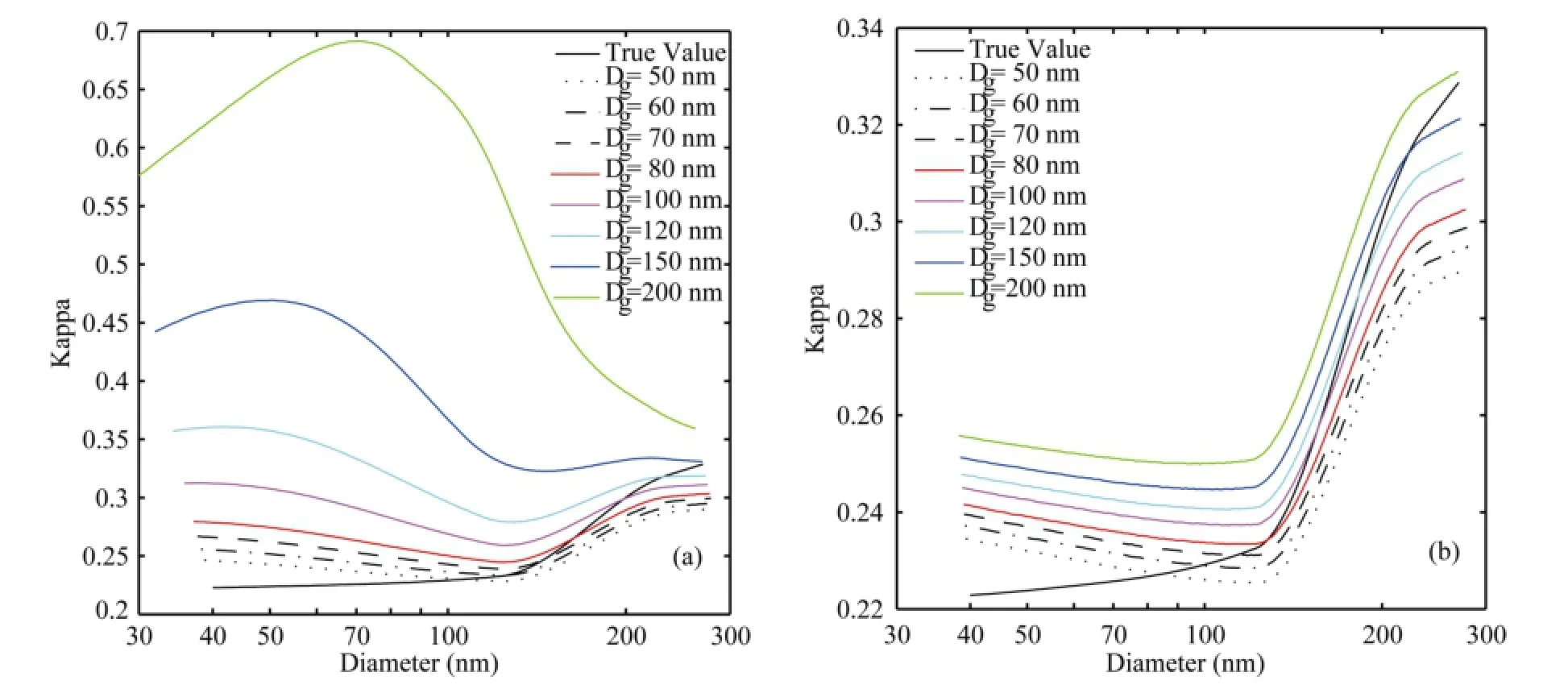
Figure 2 True values of the hygroscopicity parameter,κ, and those from measurements without data inversion with a differential mobility analyzers (DMA) sample to sheath flow ratio of 1:4. The black solid line represents the true hygroscopicity, while the others are the measurements of aerosols with different geometric mean diameters: (a) particles with all charges; (b) only singly charged particles.

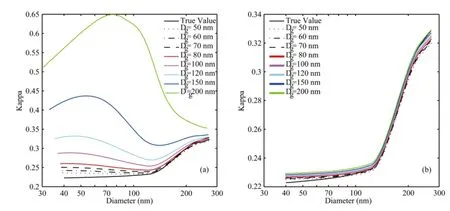
Figure 3 True values of the hygroscopicity parameter,κ, and those from measurements without data inversion with a DMA sample to sheath flow ratio of 1:10. The black solid line represents the true hygroscopicity, while the others are the measurements of aerosols with different geometric mean diameters: (a) particles with all charges; (b) only singly charged particles.

4 Conclusion and discussion

The DMA-based systems separate particles with a prescribed size by extracting the ones with a small range of electrical mobilities. Data inversion is required for measured concentrations because the selected particles are quasi-mono-dispersed and may carry more than one charge. The multiply charged particles can significantly alter the raw SRAR. Generally, the SRAR are overestimated, since the multiply charged particles are larger in size and have higher activation ratios. The effect of multiply charged particles is more prominent for PNSDs with a large fraction of super-100 nm particles, which have a larger probability of being multiply charged than smaller particles. The DMA transfer function, determined by the sample to sheath flow ratio, has a minor influence on the raw SRAR compared to the multiple charging of particles. Although a smaller sample to sheath flow ratio is favorable for reducing the deviation of measurements, the limited sampling time might result in a smaller sampling volume and increase the fluctuation error. The raw SRAR, as well as the hygroscopicity derived from the D50 of the raw SRAR, might be highly biased if the effects of multiple charging and the DMA transfer function are not corrected. The effect of the DMA transfer function and multiple charging on the raw SRAR and derived hygroscopicity parameter clearly indicates data inversion to be critical for the size-resolved CCN measurement. It is recommended that a high sample to sheath flow ratio (considering the size range and other measurement requirements) should be set to reduce the fluctuation error and the observational data should be corrected with a full inversion algorithm.

Acknowledgements. This work was supported by the National Natural Science Foundation of China (NSFC) (Grant Nos. 41205098 and 41305114) and the “Strategic Priority Research Program” of the Chinese Academy of Sciences (Grant No. XDA05100000).

Cruz, C. N., and S. N. Pandis, 1997: A study of the ability of pure secondary organic aerosol to act as cloud condensation nuclei,Atmos. Environ., 31, 2205-2214, doi:10.1016/S1352-2310(97) 00054-X.

Deng, Z. Z., C. S. Zhao, N. Ma, et al., 2011: Size-resolved and bulk activation properties of aerosols in the North China Plain,Atmos. Chem. Phys., 11, 3835-3846, doi:10.5194/acp-11-3835-2011.

Deng, Z. Z., C. S. Zhao, N. Ma, et al., 2012: A method for measuring aerosol activation ratios with high size resolution,Acta Sci. Nat. Univ. Pekin., 48, 386-392.

Deng, Z. Z., C. S. Zhao, N. Ma, et al., 2013: An examination of parameterizations for the CCN number concentration based on in situ measurements of aerosol activation properties in the North China Plain,Atmos. Chem. Phys., 13, 6227-6237, doi:10.5194/ acp-13-6227-2013.

Dusek, U., G. P. Frank, L. Hildebrandt, et al., 2006: Size matters more than chemistry for cloud-nucleating ability of aerosol particles,Science, 312, 1375-1378, doi:10.1126/science.1125261.

Frank, G. P., U. Dusek, and M. O. Andreae, 2006: Technical note: A method for measuring size-resolved CCN in the atmosphere,Atmos. Chem. Phys. Discuss., 6, 4879-4895, doi:10.5194/acpd-6-4879-2006.

Gunthe, S. S., D. Rose, H. Su, et al., 2011: Cloud condensation nuclei (CCN) from fresh and aged air pollution in the megacity region of Beijing,Atmos. Chem. Phys., 11, 11023-11039, doi:10.5194/acp-11-11023-2011.

Hagen, D. E., and D. J. Alofs, 1983: Linear inversion method to obtain aerosol size distributions from measurements with a differential mobility analyzer,Aerosol Sci. Tech., 2, 465-475,doi:10.1080/02786828308958650.

Knutson, E. O., and K. T. Whitby, 1975: Aerosol classification by electric mobility: Apparatus, theory, and applications,J. Aerosol Sci., 6, 443-451, doi:10.1016/0021-8502(75)90060-9.

Lance, S., J. Medina, J. N. Smith, et al., 2006: Mapping the operation of the DMT continuous flow CCN counter,Aerosol Sci. Tech., 40, 242-254, doi:10.1080/02786820500543290.

Li, C. C., X. He, Z. Z. Deng, et al., 2013: Dependence of mixed aerosol light scattering extinction on relative humidity in Beijing and Hong Kong,Atmos. Oceanic Sci. Lett., 6, 117-121.

Liu, H. J., C. S. Zhao, B. Nekat, et al., 2014: Aerosol hygroscopicity derived from size-segregated chemical composition and its parameterization in the North China Plain,Atmos. Chem. Phys., 14, 2525-2539, doi:10.5194/acp-14-2525-2014.

Liu, P. F., C. S. Zhao, T. Göbel, et al., 2011: Hygroscopic properties of aerosol particles at high relative humidity and their diurnal variations in the North China Plain,Atmos. Chem. Phys., 11, 3479-3494, doi:10.5194/acp-11-3479-2011.

Massling, A., M. Stock, B. Wehner, et al., 2009: Size segregated water uptake of the urban submicrometer aerosol in Beijing,Atmos. Environ., 43, 1578-1589, doi:10.1016/j.atmosenv.2008.06. 003.

Meier, J., B. Wehner, A. Massling, et al., 2009: Hygroscopic growth of urban aerosol particles in Beijing (China) during wintertime: A comparison of three experimental methods,Atmos. Chem. Phys., 9, 6865-6880, doi:10.5194/acp-9-6865-2009.

Moore, R. H., A. Nenes, and J. Medina, 2010: Scanning mobility CCN analysis-a method for fast measurements of size-resolved CCN distributions and activation kinetics,Aerosol Sci. Tech., 44, 861-871, doi:10.1080/02786826.2010.498715.

Pan, X. L., P. Yan, J. Tang, et al., 2009: Observational study of influence of aerosol hygroscopic growth on scattering coefficient over rural area near Beijing mega-city,Atmos. Chem. Phys., 9, 7519-7530, doi:10.5194/acp-9-7519-2009.

Petters, M. D., and S. M. Kreidenweis, 2007: A single parameter representation of hygroscopic growth and cloud condensation nucleus activity,Atmos. Chem. Phys., 7, 1961-1971, doi:10. 5194/acp-7-1961-2007.

Petters, M. D., A. J. Prenni, S. M. Kreidenweis, et al., 2007: On measuring the critical diameter of cloud condensation nuclei using mobility selected aerosol,Aerosol Sci. Tech., 41, 907-913, doi:10.1080/02786820701557214.

Roberts, G. C., and A. Nenes, 2005: A continuous-flow streamwise thermal-gradient CCN chamber for atmospheric measurements,Aerosol Sci. Tech., 39, 206-221, doi:10.1080/027868290913 988.

Rose, D., S. S. Gunthe, E. Mikhailov, et al., 2008: Calibration and measurement uncertainties of a continuous-flow cloud condensation nuclei counter (DMT-CCNC): CCN activation of ammonium sulfate and sodium chloride aerosol particles in theory and experiment,Atmos. Chem. Phys., 8, 1153-1179, doi:10.5194/ acp-8-1153-2008.

Rose, D., A. Nowak, P. Achtert, et al., 2010: Cloud condensation nuclei in polluted air and biomass burning smoke near the mega-city Guangzhou, China—Part 1: Size-resolved measurements and implications for the modeling of aerosol particle hygroscopicity and CCN activity,Atmos. Chem. Phys., 10, 3365-3383, doi:10.5194/acp-10-3365-2010.

Shen, X. J., J. Y. Sun, Y. M. Zhang, et al., 2011: First long-term study of particle number size distributions and new particle formation events of regional aerosol in the North China Plain,Atmos. Chem. Phys., 11, 1565-1580, doi:10.5194/acp-11-1565- 2011.

Swietlicki, E., H.-C. Hansson, K. Hämeri, et al., 2008: Hygroscopic properties of submicrometer atmospheric aerosol particles measured with H-TDMA instruments in various environments—A review,Tellus B, 60, 432-469, doi:10.1111/j.1600-0889.2008. 00350.x.

Wang, J., R. C. Flagan, and J. H. Seinfeld, 2003: A differential mobility analyzer (DMA) system for submicron aerosol measurements at ambient relative humidity,Aerosol Sci. Tech., 37, 46-52, doi:10.1080/02786820300891.

Wiedensohler, A., 1988: An approximation of the bipolar charge distribution for particles in the submicron size range,J. Aerosol Sci., 19, 387-389, doi:10.1016/0021-8502(88)90278-9.

Wiedensohler, A., W. Birmili, A. Nowak, et al., 2012: Mobility particle size spectrometers: Harmonization of technical standards and data structure to facilitate high quality long-term observations of atmospheric particle number size distributions,Atmos. Meas. Tech., 5, 657-685, doi:10.5194/amt-5-657-2012.

Wu, Z., M. Hu, P. Lin, et al., 2008: Particle number size distribution in the urban atmosphere of Beijing, China,Atmos. Environ., 42, 7967-7980, doi:10.1016/j.atmosenv.2008.06.022.

:Deng, Z.-Z., and L. Ran, 2014: Highly biased hygroscopicity derived from size-resolved cloud condensation nuclei activation ratios without data inversion,Atmos. Oceanic Sci. Lett., 7, 254-259,

10.3878/j.issn. 1674-2834.13.0116.

Received 31 December 2013; revised 24 March 2014; accepted 11 April 2014; published 16 May 2014

DENG Zhao-Ze, dengzz@mail.iap.ac.cn