Optimal Forward-Scattering Angles of Atmospheric Aerosols in North China

JIA Sheng-Jieand LÜ Da-Ren

1Key Laboratory of Middle Atmosphere and Global Environment Observation, Institute of Atmospheric Physics, Chinese Academy of Science, Beijing 100029, China

2University of Chinese Academy of Sciences, Beijing 100049, China

Optimal Forward-Scattering Angles of Atmospheric Aerosols in North China

JIA Sheng-Jie1,2and LÜ Da-Ren1

1Key Laboratory of Middle Atmosphere and Global Environment Observation, Institute of Atmospheric Physics, Chinese Academy of Science, Beijing 100029, China

2University of Chinese Academy of Sciences, Beijing 100049, China

The accurate understanding of atmospheric aerosol extinction coefficients is very important for atmospheric science research. To achieve a fast and simple method for determining the parameters, the selection of optimal forward-scattering angles of atmospheric aerosols is required. In this paper, the authors introduce the detection basis of forward-scattering of atmospheric aerosols, and the authors verify the sensitivity of the phase function to the real part of the complex refractive index. The authors use the Jaenicke urban aerosol model to determine that forward-scattering angles near 33° are suitable. However, the optimal forward-scattering angles in North China are between 37° and 40°. Numerical simulation shows that certain types of particle size distribution of newly generated particles and pollution have limited influences on the selection of forward-scattering angles. But the ranges of these insensitive angles shift ～ 10 degrees for dust intrusion, and the relative deviations of the phase function are less than 5.0% within extra angles of 0° to 3°. This study can serve as a reference for the selection of optimal forward-scattering angles for visibility meters and Present Weather Identifiers (PWIs) in addition to the detection of forward-scattering optical properties.

forward-scattering angles, phase function, complex refractive index, visibility meters

1 Introduction

Atmospheric aerosols are solid and liquid particles suspended in the atmosphere with diameters that range from ～10−3µm to 10 µm (Zhang, 1995) that originate from molecules of nucleated clusters of crustal dust up to tens of microns in cloud droplets (D’Almeida et al., 1991). Aerosol particles vary greatly in size, source, chemical composition, optical properties, amount, distribution in space and time, and lifetime in the atmosphere. However, the various factors that influence the characteristics of atmospheric aerosols are not known comprehensively thus far (Intergovernmental Panel on Climate Change (IPCC), 2007).

As a key component of aerosol research, the scattering characteristics of the anterior hemisphere of atmosphericaerosols particles ranged from 0° and 90° along the direction of the incident wave, hereinafter referred to as forwardscattering, has been studied for many years (Van de Hulst, 1957; Lü and Wei, 1978; Yang and Liou, 2000). Previous studies (Lü et al., 1981; Qiu et al., 1984) have focused mainly on theoretical and experimental analyses of the forward-scattering of atmospheric aerosols within small angles, which were used for the retrievals of size distributions and complex refractive indices of aerosol particles. Qiu and Zhou (1986) discussed the sensitivity of phase function to the scattering parameters of the atmospheric aerosols because of the potential for high accuracy and portability in measuring the atmospheric aerosol optical properties. However, limited studies have been conducted for quantitative analysis of phase function sensitivity to the complex refractive index by size distribution (Li et al., 1994; Li and Peng, 2012). In the present study, for the selection of optimal forward-scattering angles of aerosols, these sensitivities were studied quantitatively according to observational datasets and numerical simulation.

A prototype of forward-scattering Present Weather Identifiers (PWIs) was developed by the Institute of Atmospheric Physics, Chinese Academy of Science, in December 2008 in which an automatic real-time instrument was proposed that accurately measures visibility and distinguishes weather types such as fog, haze, and mist. This type of instrument is important for near-future automatic weather observations in China (China Meteorological Administration, 2006). One of the crucial functions of the instrument is the selection of optimal forward-scattering angles of atmospheric aerosols according to the observed aerosol properties in China. In Section 2 of this paper, we introduce the theoretical basis of forward-scattering detection, and the selection of optimal forward-scattering angles of atmospheric aerosols with typical aerosol models is discussed in Section 3.1. Three types of aerosol conditions including new-particle generation, pollution, and dusty weather are simulated, and the influence of their differences on the selection of optimal forward-scattering angles is discussed in Section 3.2. Finally, we summarize the optimal forward-scattering angles of atmospheric aerosols in North China in Section 3.3.

2 The theoretical basis of forward-scattering detection

Briefly, the scattering intensityI(θ) from a fixedforward-scattering angle of atmospheric aerosol particles is defined by the following equation (Liou, 2004):

whereθis the forward-scattering angle,I0is the incident energy,σsis the scattering coefficient,Ris the distance from the observation point to the scatters, andP(θ) is the normalized scattering phase function. Equation (1) can be simplified as:

wherekis the measuring constant.

Because the complex refractive index and the number concentration distributions, hereafter referred to as size distributions, of atmospheric aerosol particles change continually, quantitative analysis of the extinction coefficient by a fixed forward-scattering angle of aerosol particles requires the following criteria:

1) The phase functionP(θ) is insensitive to the complex refractive index and the particle size distribution; that is,P(θ) can be considered as a constant when theθangle changes.

2) There is no absorption effect on the aerosol particles or there is a defined linear relationship between the scattering coefficient and extinction coefficient of aerosol particles. That is

whereσeis the extinction coefficient,cis a constant, andc≤ 1.

3) The shape of aerosol particles is spherical.

The first criterion is the theoretical basis of optimal forward-scattering detection, in which the phase function is insensitive to the complex refractive index and the size distribution of aerosols. Because the types of atmospheric aerosol size distribution differ significantly among regions, it is necessary to determine the optimal forwardscattering angles according to the observed aerosol types. The scattering coefficient of aerosol particles can be calculated by Eq. (1).

For some applications related to extinction coefficients, however, such as forward-scattering visibility meters, the second criterion should be considered. Assuming that the incident wavelength is 550 nm (Han et al., 2012), the complex refractive index is generally less than 0.008 (World Meteorological Organization (WMO), 1983; D’Almeida et al., 1991) excluding some special conditions such as soot-polluted cities. In addition, according to the Mie theory (Mie, 1908), scattering energy accounts for most of the extinction energy for a high-number concentration and a larger equivalent radius of particles. In such cases, the single scattering albedo (SSA) of particles is close to 1.0.

For the third criterion, it is clear that most of the actual atmospheric aerosol particles are non-spherical. However, the differences in phase functions of spherical and non-spherical particles is negligible for forward-scattering within the forward-scattering angles from 0° to 40° for monodispersed aerosol particles (Yang and Liou, 2000) and from 0° to 50° for polydispersed particles (Liou, 2004). Therefore, to facilitate calculation, the assumption of spherical particles was used in this paper.

3 Optimal selection of forward-scattering angles

Considering the aforementioned criteria, it is necessary to determine the aerosol size distributions in the quantitative study of optimal forward-scattering angles. However, the actual aerosol size distributions undergo spatiotemporal changes. For various research purposes, scientists have proposed several aerosol size distribution models such as gamma distribution for environmental aerosol particles (Deirmendjian, 1969), Junge distribution for urban aerosol particles (Junge, 1963), and hierarchical representation distribution (Seinfeld and Pandis, 1998). In these models, lognormal distribution is used most often (Shi, 2007). For more realistic study (Jaenicke, 1993), we used the following equation to describe the aerosol size distribution:

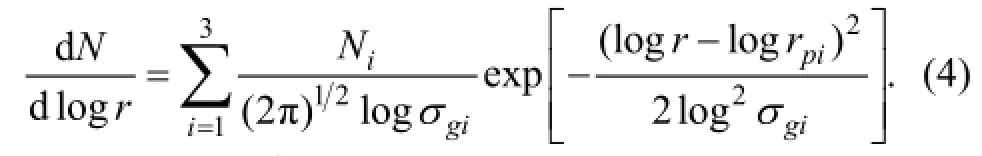
HereNi(cm−3) is the number concentration of theith bin,r(nm) is the diameter of the aerosol particle,rpi(nm) is the median diameter of theith bin, andσgiis the standard deviation of theith bin.

In the following sections (3.1-3.3), the sensitivity of phase function to the real part of the complex refractive index for typical aerosol size distributions has been studied by using the Bohren-Huffman Mie model (BHMIE; Bohren and Huffman, 1983; Wiscombe, 1996; Du, 2004). First, we tested the sensitivity by using typical aerosol models (Jaenicke, 1993). On the basis of an observed aerosol dataset obtained from Wuqing station in Tianjin, three typical aerosol size distributions were simulated. Therefore, the optimal forward-scattering angles of atmospheric aerosols were studied in North China according to the observation of a regional atmospheric background station.

3.1 Typical aerosol models

On the basis of a large number of observational data obtained from various regions, Jaenicke (1993) categorized seven typical aerosol size distributions including urban, marine, rural, remote continent, free troposphere, polar, and desert. In this section, we selected four of the distribution types that are most affected by human activities (Table 1). To better describe the size distributions, the sensitivity of phase function to the real part of the complex refractive indexR(θ,m) is defined by the follow equation:

wherem=mR− mI×iis the complex refractive index of aerosol particles,mRis the real part andmIis the imaginary part.m0= 1.5 − 0.01 ×i,mI= 0.01. The imaginary part refers to the second criterion described in Section 2.

Table 1 Variables of the Jaenicke aerosol models in four typical regions and their insensitive angles with relative deviation (RD).

Figure 1 shows the sensitivity of the phase function to the real part of the complex refractive index determined by using the Jaenicke aerosol models. The modified phase functionR(θ,m) maintained the value of 0.90 to 1.10 with aθrange of 28° to 33°, whereasmRvaried from 1.3 to 1.7 (Table 1). For the urban aerosol model (Fig. 1a), the insensitive angle is in the vicinity of 33° due to the relative deviation of less than 5.0%; the relative deviation is equal to 1-R(θ,m). This conclusion is generally applied to determine forward-scattering angles for visibility meters (Vaisala, 2002; Zeng et al., 1999). In the following section, three typical aerosol size distributions are simulated and analyzed to determine the various influences on the selection of the optimal forward-scattering angles.

3.2 Numerical simulation

In general, the size distribution and the chemical compositions of atmospheric aerosols change significantly according to various weather conditions or pollution incidents (Seinfeld and Pandis, 2006). In the present study, three representative events including new particle generation, pollution, and dust intrusion were selected, and the corresponding size distributions were simulated (Table 2). As shown in Table 2, type (a) is the observed average aerosol size distribution from Wuqing station, and types (b)-(d) are the simulation results of aerosol size distribution based on type (a) according to the three events, respectively. To better reflect the simulation results, the new particle generation (type (b)) enhanced theNvalue of mode I, and the pollution incident (type (c)) enhanced theNvalue of mode III. TheNvalue of mode I was set to zero, and theNvalue of mode IV was setting to 100 in the dust intrusion incident (type (d); Seinfeld and Pandis, 2006; Shen, 2009). The rigorously validated raw data (type (a); Ma et al., 2011) was obtained from the research data recorded during the Hachi campaign in Wuqing, Tianjin Province (Liang, 2012).

Figure 1 Sensitivity of the phase function to the real part of the complex refractive index as determined by using Jaenicke aerosol models. The color bar isR(θ,m), and (a)-(d) are urban, marine, rural, and remote continent, respectively.

Table 2 Variables of the four aerosol models under four weather conditions and their insensitive angles with relative deviation (RD).

The relative deviations of the phase function were less than 10.0% whenθchanged from 30° to 52° and were less than 5.0% near 37° (Fig. 2 and Table 2). The phase function of the new particle generation (Fig. 2b) and the pollution incident (Fig. 2c) had a limited effect in the range of the angles, but for the dust intrusion incident, these insensitive angles were in the range of 28° to 40° (Table 2). It was noted that the relative deviation was even less than 5.0% within 0° to 3° in the dust intrusion incident, in which the relative deviation would normally be above 20.0% for other weather conditions. The phenomena of unusually low relative deviation at 0° to 3° has not been reported in other studies and it will supply an additional selection for the optimal forward-scattering angle in desert areas or areas with heavy dust pollution.

It can be concluded from Figs. 1 and 2 that the insensitive angles of the phase function to the real part of the complex refractive index are in the range of 28° to 52° and vary according to the size distributions of the atmospheric aerosols. Thus, it is very important to study typical size distributions of atmospheric aerosols in various regions before determining the optimal forward-scattering angles of aerosols for inversion methods. In Section 3.3, a representative site is selected in North China as an example of such analysis.

3.3 Optimal forward-scattering detection angles in North China

The particle size distributions of atmospheric aerosols in North China were observed by the Chinese Academy of Meteorological Sciences (CAMS) at the Shangdianzi regional atmospheric background station during March 2008 to February 2009 (Shen, 2009). The observation instruments used were the Twin Differential Mobility Particle Sizer (TDMPS, IfT, Leipzig, Germany; Birmili et al., 1999) and the Aerodynamic Particle Sizer (APS Model3320, TSI, Inc., Shoreview, MN USA) that measure magnitudes of aerosols with diameters of 3 nm to 10 µm. Shen (2009) parameterized aerosol distributions to three modal lognormal size distributions according to the seasonal average of the dataset.

Figure 2 Sensitivity of the phase function to the real part of the complex refractive index under (a) the average status, (b) new-particle generation, (c) pollution incident, and (d) dusty weather based on the dataset obtained from Wuqing station.

The detailed optimal forward-scattering angles in Shangdianzi determined in the present study are shown in Fig. 3, and the parameterized distributions are shown in Table 3. It is obvious that the relative deviations of the phase function were less than 10.0% whenθwas in the range of 30° to 45°. During spring and autumn,θwas slightly smaller than that in winter and summer. However, the changes in all of the aforementioned seasonal angular ranges were significantly smaller than those in the dust intrusion incident (see Fig. 2). Furthermore, the relative deviations of the phase function were less than 5.0% when the forward-scattering angles ranged from 37° to 40° (Table 3). Because the aerosol models in Shangdianzi are typical of those in North China (Ke and Yang, 2007; Su et al., 2009), they are considered to be suitable for retrieving forward-scattering parameters, such as extinct coefficient, in this region with the same forward-scattering angles. This conclusion corresponds to the results of observational data recorded in Wuqing (Fig. 2a; Liang, 2012).

4 Conclusion

The study introduced a new detection theory based on the forward-scattering of atmospheric aerosols and presented three criteria for forward-scattering retrieval to quantitatively analyze the extinction coefficients of aerosols. The sensitivity of the phase function to the real part of the complex refractive index for typical aerosol size distributions was determined through BHMIE. The results are summarized in the following points:

1) The phase function was insensitive to the changes of the real part of the complex refractive index near 33° in the case of Jaenicke urban aerosol model (Jaenicke, 1993). The relative deviations of the phase function wereless than 5.0% at that angle. This result is the theoretical basis for the selection of forward-scattering angles for the previous instruments of visibility meters and PWIs.

Figure 3 Sensitivity of the phase function to the real part of complex refractive index recorded at Shangdianzi station during (a) spring, (b) summer, (c) autumn, and (d) winter.

Table 3 Seasonal parameterized size distributions and their insensitive angles recorded at Shangdianzi station.

2) The numerical simulation showed that the relative deviations of phase function were less than 10.0% in the forward-scattering angles from 30° to 52°, and the relative deviations were less than 5.0% in vicinity of 37°. The types of particle size distribution of new particle generation and pollution incidents had limited influence on the selection of the optimal forward-scattering angles. However, the range of these insensitive angles shifted by ～10 degrees for the dust intrusion incident, and the relative deviations were less than 5.0% within 0° to 3°. This process can be used as an additional selection method for optimal forward-scattering angles in desert areas or areas with heavy dust pollution.

3) The observational data from the Shangdianzi regional atmospheric background station showed that the optimal forward-scattering angles were in the range of 37° to 40° in North China, which had limited influence on seasonal changes of aerosol size distributions.

For accurate retrieval of the extinction coefficients of atmospheric aerosols, the optimal forward-scattering angles are needed. However, due to the variety in actual aerosol size distribution models with time, locations, species, and components, the errors from this method necessitate more discussion.

The above analysis was used as the basis for design of the forward-scattering angles of PWIs. A comparison of the measurements of PWIs with those of various forward-scattering angles by IAP and by other manufacturers should be conducted in the near future. Moreover, the aerosol models and complex refractive index under various weather conditions and regions need further study to determine the optimal forward-scattering angles for reality aerosol conditions in the entire country of China.

Acknowledgements. This study is supported mainly by the China Meteorological Administration under Grant GYHY200806031 and by the Chinese Academy of Sciences under Grant XDA05040302. The authors thank Professor Jinhuan QIU for his help with numerical simulation. The authors also thank the two anonymous reviewers for their constructive comments and suggestions.

Birmili, W., F. Stratmann, and A. Wiedensohler, 1999: Design of a DMA based size spectrometer for a large particle size range and stable operation,J. Aerosol Sci., 30(4), 549-533.

Bohren, C. F., and D. R. Huffman, 1983:Absorption and Scattering of Light by Small Particles, John Wiley, Hoboken, 530pp.

China Meteorological Administration (CMA), 2006:Meteorological Development "Eleventh Five-Year Plan" (2006-2010)(in Chinese), 21pp, available at http://www.sdpc.gov.cn/fzgggz/fzgh/ ghwb/115zxgh/200710/P020071016507296438862.pdf.

D'Almeida, G. A., P. Koepke, and E. P. Shettle, 1991:Atmospheric Aerosols: Global Climatology and Radiative Characteristics, A. Deepak Publishing, Hampton, 561pp.

Deirmendjian, D., 1969:Electromagnetic Scattering on Spherical Polydispersions, Elsevier, New York, 290pp.

Du, H., 2004: Mie-scattering calculation,Appl. Opt., 43, 1951-1956.

Han, Y., R. Z. Rao, Y. J. Wang, et al., 2012: Inversive method on atmospheric aerosol scattering phase function,Infrared Laser Eng.(in Chinese), 41(11), 3050-3054.

IPCC, 2007:Climate Change 2007:The Physical Science Basis, Contribution of Working Group I to Fourth Assessment Report of the Intergovernmental Panel on Climate Change, S. Solomon (Eds.), Cambridge University Press, Cambridge and New York, 171-180.

Jaenicke, R., 1993: Tropospheric aerosols, in:Aerosol-Cloud-Climate Interactions, P. V. Hobbs (Eds.), Academic Press, San Diego, 235pp.

Junge, C. E., 1963:Air Chemistry and Radioactivity, Academic Press, New York, 382pp.

Ke, Z. J., and J. Tang, 2007: An observation study of the scattering properties properties of aerosols over Shangdianzi, Bejing,Chinese J. Atmos. Sci.(in Chinese), 31(3), 553-559.

Li, C. W., and P. Peng, 2012: Visibility measurement using multi-angle forward scattering by liquid droplets,Measur. Sci. Tech., 23(10), 5802-5813.

Li, G. H., J. B. Zhang, H. L. Hu, et al., 1994: Sensitivity analysis of light scattering and extinction parameters to the aerosol refractive index,Acta Optica. Sinica, 14(5), 551-553.

Liang, S., N. Ma, W. J. Xu, et al., 2012: Analysis of particle size distribution measurements from a summer campaign in suburban Tianjin,Acta Sci. Nat. Univ. Pekin.(in Chinese), 48(2), 246-252.

Liou, K. N., 2004:Introduction to Atmospheric Radiation(2nd ed.), China Meteorological Press, Beijing, 614pp.

Lü, D. R., and Z. Wei, 1978: the theoretical calculation of atmospheric aerosol extinction by laser,Chinese J. Atmos. Sci.(in Chinese), 2(1), 145-152.

Lü, D. R., X. J. Zhou, and J. H. Qiu, 1981: Theory and numerical experimental study of remote sensing of atmospheric aerosol size distribution by combined solar extinction and forward scattering method,Sci. China, 12, 1516-1523.

Ma, N., C. S. Zhao, A. Nowak, et al., 2011: Aerosol optical properties in the North China Plain during HaChi campaign: An in-situ optical closure study,Atmos. Chem. Phys., 11, 5959-5973.

Mie, G., 1908: Beiträge zur optic trüber Medien speziell kolloidaler Metallösungen,Ann. Phys., 25, 377-445.

Qiu, J. H., and X. J. Zhou, 1986: Simultaneous determination of aerosol size distribution and refractive index and surface albedo from radiance. Part I: Theory,Adv. Atmos. Sci., 3(2), 162-171.

Qiu, J. H., X. J. Zhou, and Y. Z. Zhao, 1984: Theory analysis on aerosol refractive index by using remote sensing angle scattering method,Sci. China Ser. B-Chem., 10, 961-970.

Seinfeld, J. H., and S. N. Pandis, 1998:Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, John Wiley & Sons, Inc., New Jersey, 350-355.

Seinfeld, J. H., and S. N. Pandis, 2006:Atmospheric Chemistry and Physics: From Air Pollution to Climate Change(2nd ed.), John Wiley & Sons, Inc., New Jersey, 369-381.

Shen, X. J., 2009:Particle Size Distribution Measurement and Analysis at Shangdianzi in Beijing(in Chinese), M. S.’s thesis, Chinese Academy of Meteorological Sciences, 30-34.

Shi, G. Y., 2007:Atmospheric Radiation(in Chinese), Science Press, Beijing, 402pp.

Su, C., X. L. Zhang, Q. Liu, et al., 2009: Analysis of the characteristics of aerosol scattering coefficient at Shangdianzi background station,Climatic Environ. Res.(in Chinese), 14(5), 537-545.

Vaisala company, 2002:Weather Sensor FD12P User’s Guide, available at www.vaisala.com/Vaisala%20Documents/FD12P% 20User%20Guide%20in%20English.pdf, 10-24.

Van de Hulst, H. C., 1957:Light Scattering by Small Particles, Wiley, New York, 446pp.

Wiscombe, W., 1996:Mie Scattering Calculations-Advances in Technique And Fast, Vector-Speed Computer Codes, NCAR Teshnical Note TN-140+STR, National Center For Atmospheric Research, Boulder, 6-24, doi:10.5065/D6ZP4414.

WMO, 1983:Report of the Experts Meeting on Aerosols and Their Climatic Effects, Rep. WCP-55, Geneva, 107pp.

Yang, P., and K. N. Liou, 2000:Finite-Difference Time Domain Method for Light Scattering by Nonspherical and Inhomogeneous Particles, Academic Press, San Diego, 49pp.

Zeng, S. E., and G. L. Wang, 1999: Observation and instrument of visibility,J. Appl. Meteor. Sci.(in Chinese), 10(2), 207-212.

Zhang, C. C., and W. X. Zhou, 1995:Atmospheric Aerosols Tutorials, China Meteorological Press, Beijing, 328pp.

:Jia, S.-J., and D.-R. Lü, 2014: Optimal forward-scattering angles of atmospheric aerosols in North China,Atmos. Oceanic Sci. Lett., 7, 236-242,

10.3878/j.issn.1674-2834.13.0113.

Received 2 January 2014; revised 27 January 2014; accepted 21 February 2014; published 16 May 2014

LÜ Da-Ren, ludr@mail.iap.ac.cn