M1近似应用于强爆炸火球辐射输运数值模拟＊

闫 凯，田 宙，郭永辉，董 楠

（西北核技术研究所，陕西 西安710024）

辐射输运的模型问题一直是强爆炸火球数值模拟中的一个主要难点［1］。在早期的火球计算中，对辐射输运的描述往往采用根据区域划分为不同近似的方法。H.L.Brode等［2－3］对辐射输运过程的描述采用双流近似和较简单的P1近似方法。陈健华等［4］依据温度的分布采用辐射热传导近似、辐射热输出近似描述辐射输运过程。火球的发展过程中光学薄和光学厚区域同时存在，采用上述简单划分的模型不能准确描述火球的辐射场，并且由于辐射场是连续的，因此对辐射场的描述也应该采用连续的模型。王心正等［5］、田宙等［6］采用最大熵变Eddington因子P1近似，即 Minerbo近似，描述辐射输运过程，该模型可以连续地描述辐射场。

Eddington近似由于其具有计算简单、适合大规模并行计算等优点，在天体物理、强爆炸火球等领域的数值模拟中得到了广泛的应用［5－6，8－11］。如何构造一个合适的Eddington因子一直是该方法的一个难点。C.D.Levermore等［12］和A.M.Anile等［13］依据辐射熵原理分别独立地提出了一个 Eddington因子近似模型。该模型又被称为M1近似，目前已被广泛应用在天体物理的数值模拟中［8－11，14－15］，但其在强爆炸火球数值计算中的应用还未见报道。本文中，将M1近似引入到强爆炸火球的数值计算中，并将计算结果与现有辐射输运模型的计算结果进行比较。

1 计算模型

1.1 辐射流体力学方程组

本文中，采用Euler型一维球对称辐射流体动力学方程组，其基本表达式由辐射输运方程：

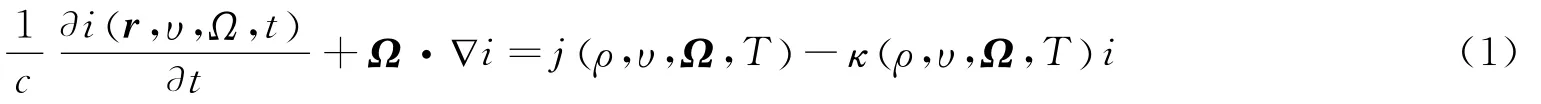
和Euler方程：

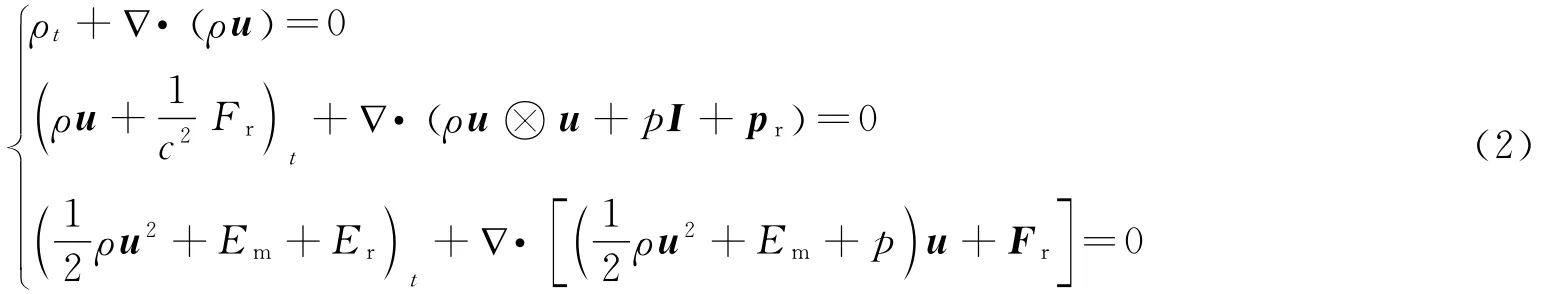
耦合构成。式中：r为空间坐标，t为时间坐标，c为光速，υ为光子运动的频率，Ω 为光子运动的方向，i为辐射强度，j为发射率，κ为吸收系数；p、ρ、u、T 分别为气体的压力、密度、速度和温度；Em为气体体积内能；I为单位矩阵；Er，Fr和pr分别为辐射能密度、辐射能流和辐射压力，其定义如下：

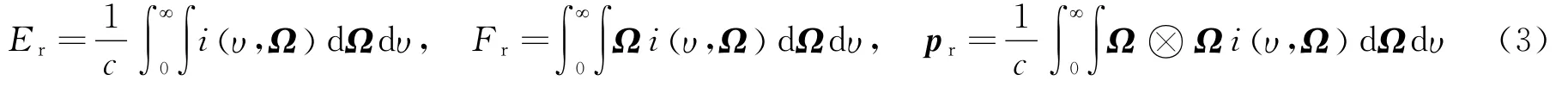
一般来说，由于光子频率、光子运动方向等引起的复杂性，直接求解辐射流体方程组是极其困难的.在强爆炸和天体物理的数值模拟中，一个常见的做法就是对辐射输运方程做角度积分，这样可以得到辐射输运的零阶矩方程和一阶矩方程组成的方程组：

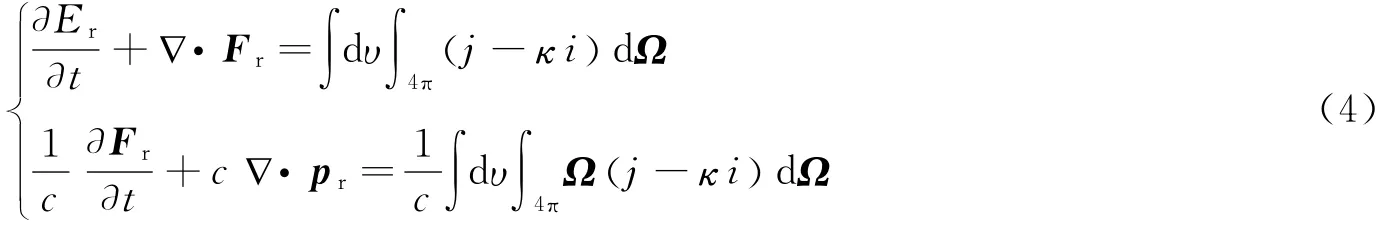
方程组（4）是辐射输运矩方程在实验室坐标系下的形式，如果考虑流体速度带来的相对论效应，方程组形式将更复杂［16－17］。如果忽略散射和相对论效应，采用局部热力学平衡、灰体近似条件，辐射输运矩方程组将简化为：

式中：κ′为考虑到受激辐射后的吸收系数，a为Boltzmann常数。

1.2 Eddington方法

辐射输运矩方程组的一个基本问题是它不封闭，以方程组（5）为例，除去流体的物理量，矩方程组有3个未知量，却只有2个方程。为了封闭方程组，一个流行的作法是引入Eddington张量f，令：

对于多维模拟，f是一个对称张量。本文中只讨论一维情形，此时f为标量。Eddington因子可以定义为：

如果f＝1/3，那么该近似就是P1近似，又称为常Eddington因子近似。对于辐射近似各向同性的辐射场，P1近似是一个很好的近似；同时，P1近似方程简单，计算量小，在强爆炸火球数值模拟早期了得到广泛应用［2－4］。P1近似的缺点也很明显，辐射波速度恒定为倍光速，它不适合描述光子在光学薄区域的传播。

20世纪70年代，G.N.Minerbo［7］发现辐射强度角分布与辐射能流Fr定义的方向的方位角无关，其根据最大熵原则对Eddington因子f给出了一个有理逼近式：

式中：R为各向异性因子，R＝0～1。R＝0，意味着辐射场为各向同性；R＝1，即光子朝一个方向运动。该模型构建的f具有一般Eddington因子都具有的性质，即f（0）＝1/3，f（1）＝1，f（R）随R 的增大而增大。王心正等［5］和田宙等［6］利用该模型对强爆炸早期火球进行了数值模拟，取得了较好的效果。

1.3 M1近似

A.M.Anile等［13］分析了一维辐射输运矩方程组，提出Eddington因子应该满足以下条件：

（1）由于f是辐射输运方程归一化的二阶矩，因此需要满足R2≤f≤1；

（3）在光子朝一个方向运动时，应满足f（1）＝1；

（4）f应该是R 的一个凸函数，即f″（R）≥0；

（5）在自由流中，奇异点应该以光速传播；

（6）能流限制器应随各向异性因子的增大而减小，由此推出f′（R）－2R≤0。

最后，A.M.Anile等根据辐射熵原理构造的Eddington因子表达式为：

该表达式最早被 C.D.Levermore［12］提出，目前已被广泛应用于天体物理的数值模拟中［8－11］，在强爆炸火球的数值计算中则未见报道。

2 一维辐射输运矩方程的特征值问题

假定辐射波在真空中传播，则此时可忽略耦合项，辐射压力采用Eddington因子的表达式，则一维辐射输运矩方程组可以写成：

容易证明P1近似和M1近似下的一维辐射输运矩方程属于双曲型方程。对于双曲方程，其特征值可以反映方程特征波的波速。针对不同的辐射压力模型，可以计算得到其最大特征值随各向异性因子R的变化关系。其法向通量的Jacobi矩阵为：

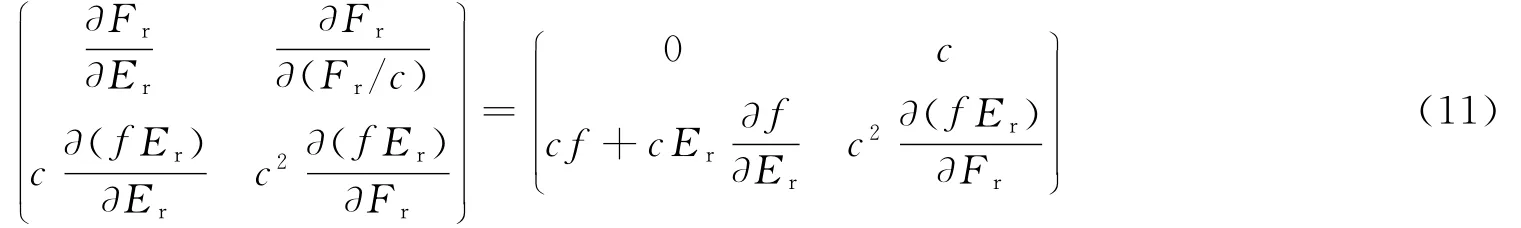
考虑Fr＞0的情况，此时：

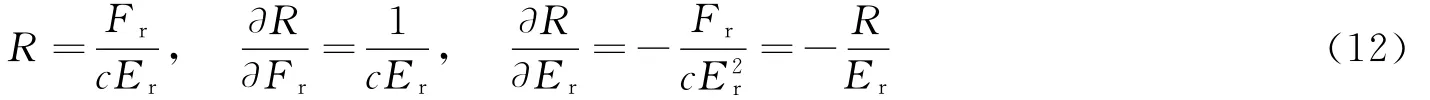
通过化简Jacobi矩阵的变量，可以得到：

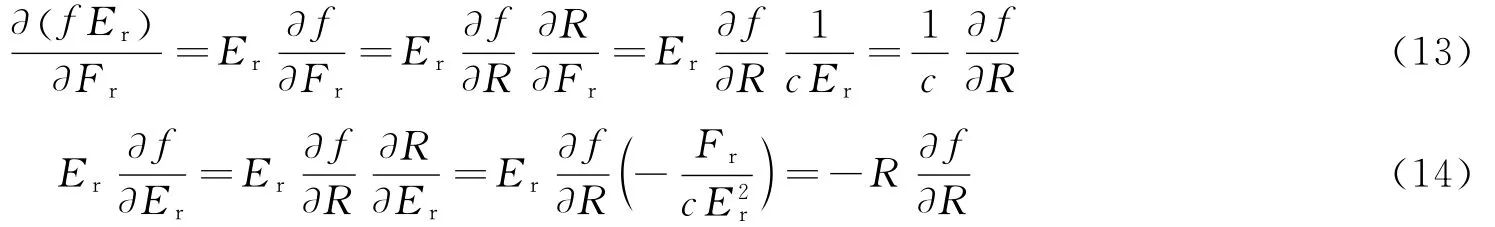
对于 Minerbo近似［7］：

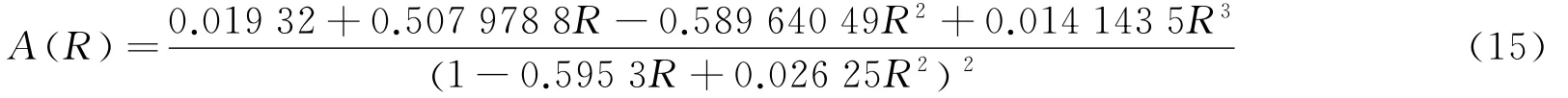
对于 M1近似［13］：

Jacobi矩阵的特征值可以表示为：

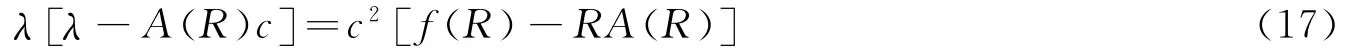
则矩阵的最大特征值应该为：

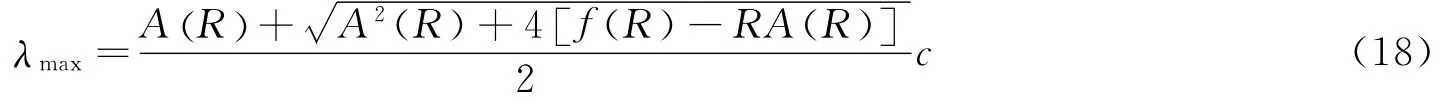
图1给出了不同近似模型中Eddington因子f随各向异性因子R的变化关系。从图中可以看出，变Eddington因子P1近似和M1近似所构造的Eddington因子均符合一般Eddington因子的性质，但不能区分两者之间优劣。

图2给出了不同近似下辐射输运矩方程的最大特征值λmax与各向异性因子R的关系。从图中可以看出，P1近似下的辐射波波速与R无关，其速度为恒定值；Minerbo近似在R比较大的时候出现了较明显的超光速现象，R＝1时其辐射波波速接近1.2倍光速；M1近似下的辐射波波速在R＝0时，即各向同性时，与P1近似下的辐射波波速一致，R＝1时，即光子朝一个方向运动时，辐射波波速和光速一致。由于辐射输运方程组的最大特征值实际反映了辐射波波速，因此可以看出，在M1近似下得到的辐射波波速更符合物理规律。对于Fr＜0的情况，可以得到类似的结果，这里不再赘述。

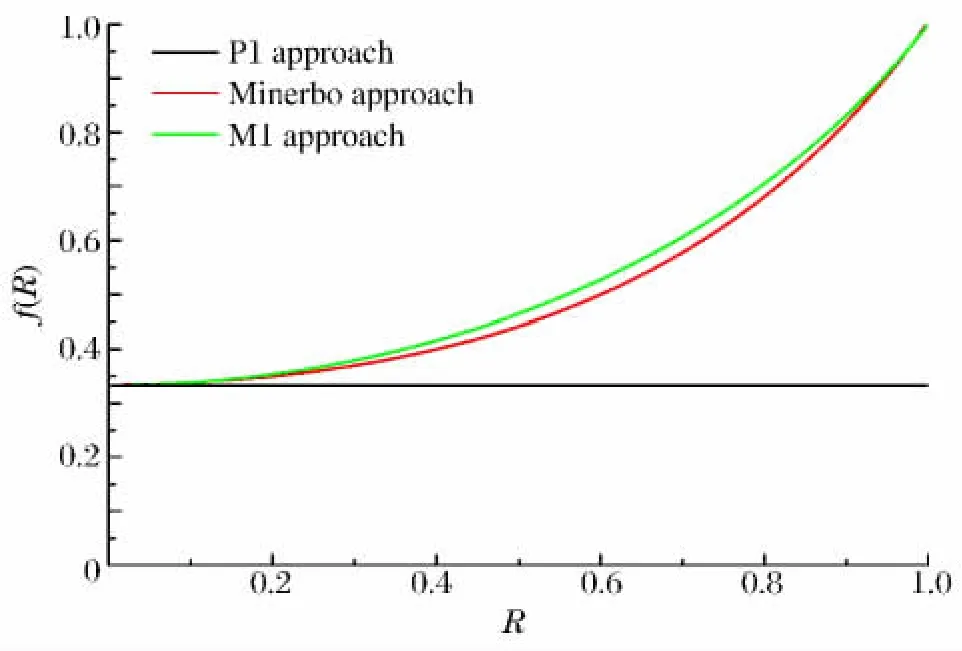
图1 不同近似下Eddington因子随各向异性因子的变化Fig.1Eddington factor varied with anisotropy factor for different approach models

图2 不同近似下辐射输运矩方程的最大特征值随各向异性因子变化Fig.2The largest eigenvalues of moment equations of radiative transfer varied with anisotropy factor for different approach models

3 强爆炸火球的数值模拟

本文中，利用M1近似构造的辐射输运模型对一维强爆炸火球问题进行数值模拟，并将计算结果与已有结果进行比较。

计算中选取的强爆炸当量为1kt TNT，等压球半径为0.75m。源区物质等价于实际气体，其密度为海平面空气密度；初始时刻火球为等压球，处于辐射平衡状态；火球内边界采用对称条件，外边界采用透射条件。图3给出了采用M1近似计算得到的1kt TNT当量下强爆炸的火球阵面和冲击波走时以及 H.L.Brode［2］和田宙等［6］的计算结果。

H.L.Brode［2］对辐射输运方程的描述采用了双流近似，即火球内部采用P1近似、外部采用辐射热输出近似。图3中火球阵面的传播过程分为辐射扩张阶段、过渡阶段和冲击波传播阶段，对应火球扩张的主要原因分别是辐射输运、辐射输运与流体力学过程共同作用和冲击波扩张。在火球扩张的前0.2μs，采用M1近似得到的火球阵面刚开始超过了H.L.Brode［2］计算得到的火球阵面，这是由于在早期X射线火球处于非平衡辐射扩散中，各向异性因子R接近1，因此采用M1近似计算得到的辐射热波传播速度高于采用双流近似的情况。0.2μs后的一段时间内，火球内部开始接近辐射平衡，M1近似下的辐射热波速度下降很快，而双流近似下的辐射热波传播速度受辐射输运的影响较小，因此出现M1近似下的辐射波阵面落后双流近似的情况。几微秒后，火球进入过渡阶段，辐射输运对火球阵面的扩张作用越来越小，因此采用这2种方法计算得到的火球阵面趋于一致。由于双流近似中没有考虑辐射压力对热空气动量的影响，因此双流近似下得到的弹壳冲击波阵面明显落后于M1近似下得到的弹壳冲击波阵面。后期，辐射输运的影响越来越弱，因此采用这2种近似得到的结果又趋于一致。

在强爆炸火球数值模拟中，本文中采用的空气状态方程和吸收系数均与田宙等［6］采用的条件一致，因此两者的结果最具有对比性。田宙等［6］在强爆炸火球数值模拟中对辐射输运方程的描述采用了变Eddington因子P1近似，即Minerbo近似。图3中M1近似下的火球阵面落后于Minerbo近似下的计算结果［6］；而M1近似下的弹壳冲击波的产生时间及走时均与Minerbo近似下的计算结果［6］一致。值得注意的是，在火球发展的中后期，即过渡阶段及以后，M1近似下的辐射波和冲击波走时与双流近似下的计算结果［2］和Minerbo近似下的计算结果［6］均符合较好，这说明不同的辐射输运模型对辐射扩张阶段计算结果的影响较明显，而对火球发展的过渡阶段及冲击波扩张阶段计算结果的影响开始减弱。

图3 采用M1近似计算得到的强爆炸的火球阵面和冲击波走时与已有结果［2，6］的比较Fig.3Fireball and shock wave fronts calculated by MI approach compared with existent results［2，6］

4 结 束 语

针对P1近似只适合于光学厚区域，Minerbo近似在光学薄区域出现了超光速现象等问题，本文中将M1近似模型引入到强爆炸火球数值计算中，并比较了3种不同辐射输运模型下火球阵面和冲击波阵面走时的计算结果。数值实验结果表明，在火球辐射的扩张阶段采用不同的辐射输运模型得到的计算结果有较明显的区别，初步定性分析了本文中采用模型的合理性，下一步将进一步定量验证M1近似模型用于强爆炸火球数值模拟的合理性。

［1］ 乔登江.核爆炸物理概论［M］.北京：国防工业出版社，2003：169 －262.

［2］ Brode H L.Fireball phenomenology［R］.The RAND Corporation.AD0612197，1965.

［3］ Brode H L，Hillendahl R W，Landshoff R K.Thermal radiation phenomena.Volume V：Radiation hydrodynamics of high temperature air［R］.AD0672837，1967.

［4］ 陈健华，王心正，谢龙生，等.均匀空气中的强爆炸一维辐射流体力学数值解［J］.爆炸与冲击，1981（2）：37 －49.Chen Jian －hua，Wang Xin －zheng，Xie Long －sheng，et al.A one －dimensional radiation hydrodynamic numerical solution for a strong explosion in uniform atmosphere［J］.Explosion and Shock Waves，1981（2）：37 －49.

［5］ 王心正，隋卫星.高空核爆炸火球的二维辐射流体力学计算［J］.计算物理，1987，4（2）：159 －168.Wang Xin －zheng，Sui Wei －xing.Two －dimension radiation hydrodynamics calculation of the high －altitude fireball［J］.Chinese Journal of Computational Physics，1987，4（2）：159 －168.

［6］ 田宙，乔登江，郭永辉.强爆炸早期火球现象的一维数值研究［J］.计算物理，2010，27（1）：8 －14.Tian Zhou，Qiao Deng－jiang，Guo Yong －hui.A one －dimensional numerical study on early fireball in strong explosion［J］.Chinese Journal of Computational Physics，2010，27（1）：8 －14.

［7］ Minerbo G N.Maximum entropy Eddington factors［J］.Journal of Quantitative Spectroscopy and Radiative Transfer，1978，20（6）：541 －545.

［8］ Kumholz M R，Klein R I，Mckee C F，et al.Equations and algorithms for mixed －frame flux －limited diffusion radiation hydrodymics［J］.The Astrophysical Journal，2007，667（1）：626 －643.

［9］ Seaid M，Klar A，Dubroca B.Flux limiters in the coupling of radiation and hydrodynamic models［J］.Journal of Computational and Applied Mathematics，2004，168（1/2）：425 －435.

［10］ Buer C，Despres B.Asymptotic preserving and positive schemes for radiation hydrodynamics［J］.Journal of Computational Physics，2006，215（2）：717 －740.

［11］ Swesty F D，Myra E S.A numerical algorithm for modeling multigroup neutrino －radiation hydrodynamics in two spatial dimensions［J］.The Astrophysical Journal Supplement Series，2009，181（1）：1 －52.

［12］ Levermore C D.Relating Eddington factors to flux limiters［J］.Journal of Quantitative Spectroscopy and Radiative Transfer，1984，31（2）：149 －160.

［13］ Anile A M，Pennisi S，Sammartino M.A thermodynamical approach to Eddington factors［J］.Journal of Mathematical Physics，1991，32（2）：544 －555.

［14］ Brunner T A，Holloway J P.One －dimensional Riemann solvers and the maximum entropy closure［J］.Journal of Quantitative Spectroscopy and Radiative Transfer，2001，69（5）：543 －566.

［15］ Buet C，Despres B.Asymptotic analysis of fluid models for the coupling of radiation and hydrodynamics［J］.Journal of Quantitative Spectroscopy and Radiative Transfer，2004，85（3/4）：385 －418.

［16］ Castor J I.Radiation hydrodynamics［M］.Cambridge，UK：Cambridge University Press，2004：213 －245.

［17］ Pomraning G C.The equations of radiation hydrodynamics［M］.Dover：Dover Publications Inc，2005：427 －505.