傅里叶望远镜对实际有纵深目标成像的研究
董 磊
(中国科学院长春光学精密机械与物理研究所,吉林 长春130033)
1 引言
傅里叶望远镜具有合成孔径和主动照明的优势,可以对远距离静止或运动目标高分辨率成像,成为近年来激光主动成像领域的热点研究对象[1-4]。在已有的研究中,不论是计算机仿真[5-9]还是室内[10-12]或外场实验[13-15],所采用的目标均是平面合作目标。有时为了模拟真实目标的漫反射特性,在目标的前面或后面放置透射式漫射体,产生和真实目标类似的漫散射效果。然而真实目标不是平面的,而是有一定的纵向深度,并且纵深是渐变的,或者局部阶梯变化。这相当于平面目标被分割成小块,块与块之间存在轴向距离。对于纵深变化的目标,其整体散射回波将不再同步,而是由大量彼此间有一定时间延迟的局部回波组成。局部回波在时间上的错位将引起解调信号时间频谱的展宽,有可能降低重构图像的质量,严重则造成无法成像。
由此可知开展傅里叶望远镜对实际有纵深目标的成像研究具有重要意义,它决定了成像系统是否可以对实际目标高分辨率成像。文章后续部分的安排如下:在原理分析部分从成像基本公式入手,引出有纵深目标散射回波信号存在时间延迟问题;然后在仿真分析部分,通过先定性后定量的方式逐步揭示回波相对延迟及目标分块数目对成像结果的影响;随后在讨论和建议部分给出避免重构图像质量下降所需信号外差频率范围以及对短脉冲激光成像提出建议;最后对全文进行总结。
2 原理分析
傅里叶望远镜的成像原理,简单来说,就是利用地面不同的二维基线的选择,在目标平面处产生不同取向和周期的干涉条纹,从而可以获取目标不同空间频率的频谱信息,然后利用傅里叶逆变换重构目标图像。其原理的出发点基于任何二维图像均可以利用不同空间频率的周期性条纹叠加而成。由此也可以看出,傅里叶望远镜成像是针对二维平面目标,如果目标本身有一定的纵向深度或者中心和边缘的纵向厚度不一样,则或许影响成像效果甚至无法成像。该问题更具体的分析可基于常见的成像基本公式。
傅里叶望远镜成像原理的基本公式为[1]:
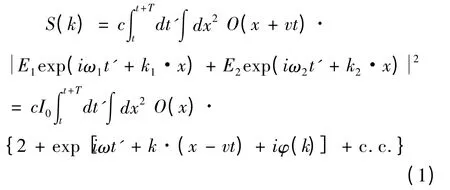
其中,S(k)代表目标散射的瞬时回波信号,由公式(1)可以看出该信号正比于目标反射率O(x+vt)和相干光场E1exp(iω1t'+k1·x)与E2exp(iω2t'+k2·x)在目标表面形成的干涉条纹光强的乘积在目标平面处的积分,c.c.代表前面指数项的复共轭。公式(1)中,c代表积分常数;每束发射光波在目标处单独产生的光强;ω=ω1-ω2为两束光之间的外差频率;v为目标运动速度。k=k0Δx/z,其中k0为光波数,Δx为两个发射光束在地面的距离矢量即基线矢量,z为目标离地面的距离。由此可以看出空间频率k与地面基线矢量Δx同向,而地面基线矢量为地平面内的二维矢量,故k平行于地平面。只有目标平面平行于地面时,k才能同时代表目标处条纹的空间频率,所以从成像基本公式可以看出空间频率k,地平面和目标平面三者互相平行。
我们可以先简单分析一下公式(1)所代表的理想情况。按照公式(1),探测器测量到的瞬时光强正比于目标反射率和干涉条纹光强的乘积在目标平面处的积分。该积分为对空间坐标的二维积分,和时间参数无关,当二维空间积分完成后,再对采样周期内的信号进行时间积分。这说明在理想情况下,目标任何一个局部散射的回波信号到达探测器的时间均相同,或者说每个局部散射的回波信号能够彼此无相对延迟地叠加。而对于有一定纵深的目标,每个局部的散射回波彼此间存在相对延迟。
以目标中心与边缘的纵向深度差为1 m为例,如图1所示,局部1与局部2的纵深差为1 m,则局部1与局部2散射回波的时间延迟差为(1 m×2)/(3×108m/s)=6.7 ns。考虑到大气湍流引起不同光束光程的变化一般为几十个波长量级,故光程差应小于1 mm,时间延迟差小于1 mm/(3×108m/s)=3.3 ps。该值远小于目标纵深差引起的时间延迟差,故可以忽略大气湍流的影响。上面的分析将初始问题转化为,目标不同局部散射回波信号有最大6.7 ns时间延迟时,叠加后的信号经过时间解调的结果是否会明显偏离理想情况。在后续的仿真分析部分将采用先定性后定量的方法,对该问题进行更加具体的研究。

图1 纵深为1m的目标Fig.1 Object with depth of 1 meter
3 仿真分析
首先尝试进行定性分析。假如信号周期比时间延迟6.7 ns大很多,如图2所示,比如150 kHz外差信号的周期为6.7μs。该值远大于6.7 ns,也就是说,不同信号的延迟(<6.7 ns)相对于信号周期可以被忽略,不同信号在时间上近似是同步的或者对准的,故经过时间解调后的结果不会明显偏离理想情况。相反,假如信号周期和时间延迟6.7 ns差不多,如图3所示,比如信号频率为150 MHz,则对应周期恰好为6.7 ns。该时间延迟相对于信号周期就无法被忽略,经过时间解调后的结果很可能明显偏离理想情况。
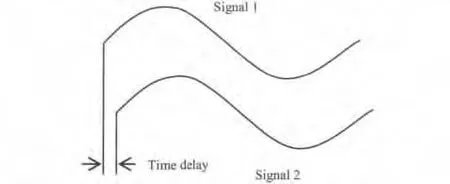
图2 信号周期远大于时间延迟Fig.2 Signal period much larger than time delay
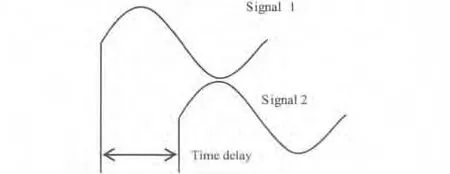
图3 信号周期与时间延迟接近Fig.3 Signal period similar to time delay
下面将利用matlab软件开展定量仿真分析。仿真的主要步骤如下:对不同时间延迟情况分别建模,并与无延迟情况的图像重构结果相比较,找出较好重构结果对应的时间延迟范围。然后改变目标分块数目,比较不同纵深的分块数目的变化对重构结果的影响,从而找出较好重构结果对目标分块数目的要求。
3.1 不同时间延迟的成像仿真
为了简单起见,假设目标由纵向深度不同的两部分组成,每部分的回波时间延迟不同。仿真采用3种不同形状的卫星目标,目标图片是分辨率为33×33的灰度图片。成像仿真中的回波延迟采用两回波相对延迟差与信号周期之比来表示,由小至大分别为:0,1/128,1/64,1/32,1/16,1/8。所有回波信号持续时间为4个周期,时间解调持续时间也是4个周期。考虑到信号不可避免受到噪声的影响,在回波信号中加入信噪比为100的随机噪声。
衍射受限目标,重构图像及其对应的Strehl值分别如图4所示。从3种不同目标图像随回波延迟增加的变化趋势可以看出,当目标不同纵深的两部分的回波延迟差为信号周期的1/32时,还能够识别重构目标的轮廓,此时重构图像的Strehl值一般大于0.2。当回波延迟差大于信号周期的1/16时,无法识别重构目标,此时重构图像的Strehl值小于0.1。

图4 衍射受限目标与重构图像的比较Fig.4 The comparison between diffraction-limited object and reconstructed images
3.2 不同纵深分块数目的成像仿真
前面的仿真假设目标由纵深不同的两部分组成,而实际目标的纵深变化往往是渐变的,产生不同延迟的大量回波。回波数目的增加是否影响重构质量是值得研究的问题,下面将比较分块数分别为2,4,8时,重构图像及其Strehl值的变化。
仿真仍采用3种不同目标的分辨率为33×33的灰度图片作为目标图像。分块数为4和8时,回波信号的延迟等间隔分布,间隔与信号周期之比分别为1/128,1/256。分块数为2、4和8时,回波信号的最大延迟与周期之比分别为7/256,6/256,7/256,分布在0.02~0.03之间,小于1/32。每种分块数各重构5次,取最好结果,如图5所示。
从图5中3种不同目标的重构结果可以看出,分块数增加并没有使成像质量下降。由此推知当目标纵深连续变化时,产生大量回波信号,只要回波信号的最大延迟差与信号周期之比小于1/32,则可重构出可识别的目标图像。从中还看出分块数为2时,Strehl值明显低于分块数为4和8对应的Strehl值。对该情况的初步判断是,分块数为2时,最大延迟的两端各对应50%的回波信号,而分块数为4或8时,最大延迟的两端各对应的回波信号比重明显下降,分别为25%和12.5%。我们知道最大延迟越小,则图像质量越好,所以最大延迟对应信号的比重降低使得重构图像质量提高。

图5 分块数分别为2、4和8的重构图像的比较Fig.5 The comparison of reconstructed images with 2,4 or 8 parts
4 讨论与建议
至此可以对原理分析中提出的问题给出明确地回答。纵深差为1 m时,对应回波最大时间延迟时为6.7 ns。如果信号周期大于6.7 ns×32=214.4 ns,即外差频率低于4.66 MHz,则回波信号经过时间解调和重构算法处理后能重构出可识别的目标。信号的外差频率越低,则重构图像质量越高。一般空间目标的纵深为10 m以内,对应的最大时间延迟小于67 ns,则采用外差频率低于466 kHz的信号可重构出可识别目标图像。
低外差频率对于连续或则宽脉冲激光成像的影响小,然而对于短脉冲激光成像则有明显影响。傅里叶望远镜成像要求时间解调持续时间为整数倍信号周期,否则成像出现混乱。然而对于超远距离成像,为了提高激光峰值功率必然会压缩脉宽,脉宽有可能压缩到几十纳秒。为了满足时间解调整数倍信号周期的要求,则一个脉冲内至少包含1个周期的信号。这时信号周期持续时间正好位于回波最大延迟时间以内,图像重构结果将是混乱的,无法识别。或许可以采用延迟补偿的方法,对目标不同部位的回波延迟差进行补偿,然而补偿的前提是事先知道目标不同部位的纵深分布,这显然是困难的。或许也可以采用多脉冲拼接的方法[16],降低加载到短脉冲激光上外差信号的频率,这在理论上是可行的,但具体实现较为复杂,还需要进一步的研究。
5 结论
本文开展针对傅里叶望远镜对实际有纵深目标成像的研究。研究发现实际目标的回波信号不再同步,而是由大量彼此存在延迟的局部回波信号组成。对于纵深变化为米级的目标,其回波最大延迟范围约10 ns,只要信号周期远大于该值,则目标纵深变化对成像无明显影响。只要信号周期远大于回波最大延迟,目标纵深连续变化或阶梯变化对成像结果无明显影响。如果信号周期与回波最大延迟相当或则更小,则重构图像质量严重下降,甚至无法成像。对于脉宽与米级纵深目标的回波最大延迟相当的短脉冲激光成像,或许可以采用多脉冲拼接的方法降低信号外差频率以实现对实际目标的高分辨率成像。
[1] Holmes R B,Ma S,Bhowmik A,et al.Analysis and simulation of a synthetic aperture technique for imaging through a turbulent medium[J].J.Opt.Soc.Am.A,1996,13(2):351-364.
[2] V L Gamiz,R B Holems,S R Czyzak,et al.GLINT:program overview and potential science objectives[C].Proceedings of International Society for Optics and Photonics,2000,4091:304-315.
[3] LIU Xinyue,DONG Lei,WANG Jianli.Fourier telescopy imaging via sparse sampling[J].Optics and precision engineering,2010,18(3):521-527.(in Chinese)刘欣悦,董磊,王建立.稀疏采样傅里叶望远镜成像[J].光学 精密工程,2010,18(3):521-527.
[4] YU Shuhai,WANG Jianli,DONG Lei,et al.Introduction of dominating factors of multiple beam FT imaging quality[J].Laser&Infrared,2011,41(12):1341-1345.(in Chinese)于树海,王建立,董磊,等.多光束傅里叶望远镜成像质量主要因素分析[J].激光与红外,2011,41(12):1341-1345.
[5] Mikhail Belen'kii,Kevin Hughes,Tim Brinkley,et al.Residual Turbulent scintillation effect and impact of turbulence on the fourier telescopy system[C].Proceedings of International Society for Optics and Photonics,2004,5160:56-67.
[6] DONG Lei,WANG Bin,LIU Xinyue.Introduction to key techniques of multiple beam Fourier telescopy[J].Chinese journal of optics and applied optics,2010,3(5):440-445.(in Chinese)董磊,王斌,刘欣悦.多光束傅里叶望远镜的关键技术[J].中国光学与应用光学,2010,3(5):440-445.
[7] YE Suo,LIU Yi,WU Jian.Effects of antenna array configurations on imaging quality in Fourier telescopy[J].High Power Laser and Particle Beams,2011,23(3):611-616.(in Chinese)叶溯,刘艺,吴健.傅里叶望远术中天线阵列配置对成像质量的影响[J].强激光与粒子束,2011,23(3):611-616.
[8] LUO Xiujuan,ZHANG Yu,SUN Xin,et al.Energy design of fourier telescope system in the atmospheric environment[J].Acta Optica Sinica,2013,33(8):0801004-1-8.(in Chinese)罗秀娟,张羽,孙鑫,等.大气环境中傅里叶望远镜系统能量设计[J].光学学报,2013,33(8):0801004-1-8.
[9] YU Shuhai,WANG Jianli,DONG Lei,et al.Time region signal collecting method of Fourier telescopy based on non-uniform periodically sampling[J].Chinese Optics,2013,6(3):395-401.(in Chinese)于树海,王建立,董磊,等.基于非均匀周期采样的傅里叶望远镜时域信号采集方法[J].中国光学,2013,6(3):395-401.
[10]DONG Lei,LIU Xinyue,WANG Jianli.The realization of fourier telescope technology in laboratory[J].Optics and precision engineering,2008,16(6):999-1002.(in Chinese)董磊,刘欣悦,王建立.实验室环境内傅里叶望远镜技术 的 实 现[J].光 学 精 密 工 程,2008,16(6):999-1002.
[11]CHEN Wei,LI Quan,WANG Yangui.Experimental research of fourier telescopy imaging system[J].Acta Optica Sinica,2011,31(2):0311001-1-6.(in Chinese)陈卫,黎全,王雁桂.傅里叶望远术成像系统的实验研究[J].光学学报,2011,31(2):0311001-1-6.
[12]ZHANG Yan,YANGChunping,GUOJing,et al.Spectrum extraction mode for fourier telescopy in laboratory[J].High Power Laser and Particle Beams,2011,23(3):571-576.(in Chinese)张炎,杨春平,郭晶,等.实验室中傅里叶望远术频谱抽取方式[J].强激光与粒子束,2011,23(3):571-576.
[13]Cuellar E L,Stapp J,Cooper J.Laboratory and field experimental demonstration of a Fourier telescopy imaging system[C].SPIE,2005,5896:58960D1-15.
[14]CHEN Baogang,DONG Lei,LIN Xudong.Segmented mirror of fourier telescope field experimental system[J].Acta Photonica Sinica,2011,40(1):87-91.(in Chinese)陈宝刚,董磊,林旭东.傅里叶望远镜外场实验系统拼接主镜[J].光子学报,2011,40(1):87-91.
[15]DONG Lie,LIU Xinyue,CHEN Baogang,et al.Field experiment and result analysis of fourier telescopy[J].Acta Photonica Sinica,2011,40(9):1317-1321.(in Chinese)董磊,刘欣悦,陈宝刚,等.傅里叶望远镜外场实验与结果分析[J].光子学报,2011,40(9):1317-1321.
[16]DONG Lei,LIU Xinyue,LIU Jie,et al.Demodulation of part period signal of fourier telescope and effects for imaging[J].Acta Photonica Sinica,2013,42(4):447-450.(in Chinese)董磊,刘欣悦,刘杰,等.傅里叶望远镜部分周期信号解调及对成像的影响[J].光子学报,2013,42(4):447-450.

