一类具有储备部件的人-机可修复系统算子性质

韩筱爽，方明

(1.延边大学科学技术学院，吉林延吉133002;2.延边大学理学院数学系，吉林延吉133002)

0 引言

Yang Nianfu[1]研究了具有两个运行部件，一个储备部件，系统故障修复时间服从一般分布的人-机系统模型的可靠性.两个部件并联的可修复系统是可靠性理论中的一个经典可修系统[3].方明[5]研究了系统解的存在唯一性.姜英秀[6]研究了系统解的指数稳定性.方明[7]研究了系统解的谱特性.

本文运用A.Pazy[2]与夏道行[4]的C0半群的理论，证明了系统算子是稠定的预解正算子，得出了系统算子的共轭算子及其定义域，并证明了系统算子的增长界为0，最后运用预解正算子中共尾的概念及其相关理论，证明了系统算子的谱上界也是0.

1 模型介绍

如图1所示，该系统为并联冗余系统，其中两个部件并联工作，一个冗余部件处于储备状态，任何时刻只要有一个部件正常工作均能使系统正常运行，工作部件中任何一个发生故障，储备部件立即补充进入工作状态，并且部件间的替换过程是自动且瞬时完成的.若系统出现部件故障则修复程序立即启动，若所有部件均发生故障则整个系统故障.此系统的工作流程如右图所示:i=0表示两个运行部件和一个储备部件均处于完好状态;i=1表示一个运行部件因硬件错误而故障，一个储备部件立即补充运行;i=2表示系统仅有一个部件正常运行而无储备部件;i=3表示系统由于硬件错误而处于故障状态;i=4表示系统由于通常错误而处于故障状态;i=5表示系统由于临界人为错误而处于故障状态.

上述的模型可由以下积分-微分方程描述:

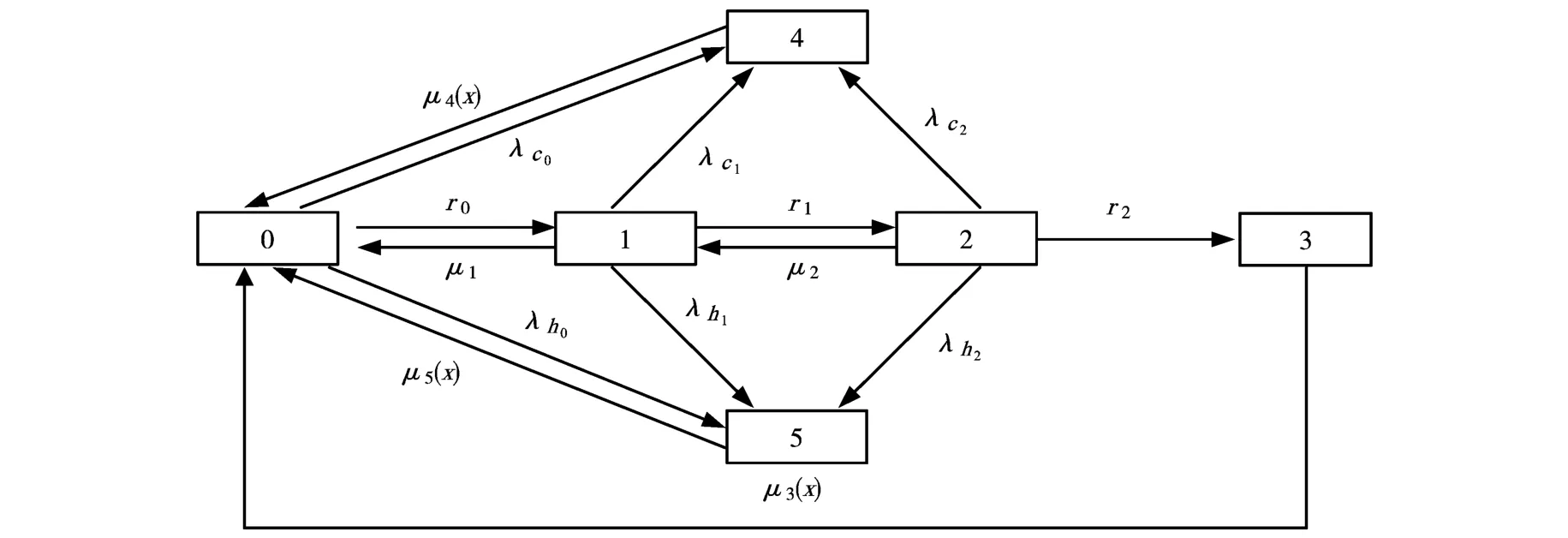
图1 系统工作流程图

其中

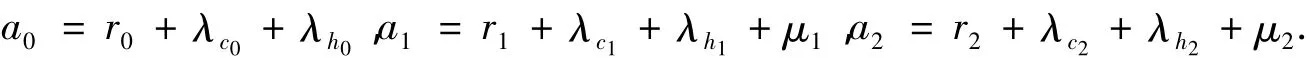
相关边值条件如下:

其中

i，j表示系统所处状态数;

ri表示系统处于状态i的定常硬件故障率(i=0，1，2);

μi表示系统处于状态i的定常硬件修复率(i=1，2);

μj(x)表示系统处于状态j，修复时间x的系统修复率(j=3，4，5);

λci表示系统从状态i到状态4的定常通常故障率(i=0，1，2);

λhi表示系统从状态i到状态5的定常临界人为故障率(i=0，1，2);

pi(t)表示在时刻t处于状态i的概率(i=0，1，2);

pj(x，t)表示系统在时刻t处于状态j，修复时间x概率且仅在t＞0时有定义(j=3，4，5).这里假定

以下将基于上述假定，讨论系统算子的性质.取状态空间

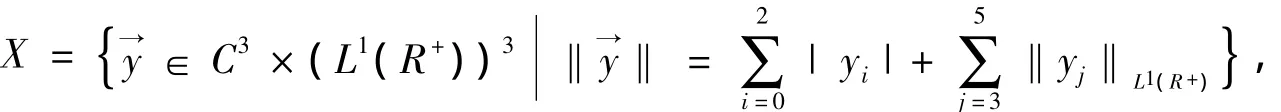
显然(X，‖·‖)是一个Banach空间，在X上定义算子

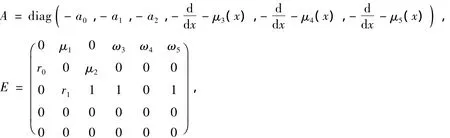
其中

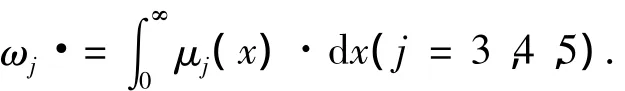
取A的定义域

则系统积分-微分方程组可描述为Banach空间中的一个抽象Cauchy问题:

2 算子性质

定义1算子A+E的谱上界定义为s(A+E)=inf{ω∈R|(ω，∞)⊆ρ(A+E)}.

定义2若算子A+E是半群T(t)的无穷小生成元，则增长界定义为

定义3E的子集C称为在E中共尾(cofinal)，若满足对每个f∈E，存在g∈C，使得f≤g.

定理4 D(A+E)在X中稠密.

证明在文[7]中已证得D(A)在X中稠密，由于D(E)=X，故D(A+E)也在X中稠密.

定理5 A+E是预解正算子.

证明对任意给定的y→∈X，考虑预解方程[vI－(A+E)]P→=y→，其等价于方程组

结合相关边值条件，解得

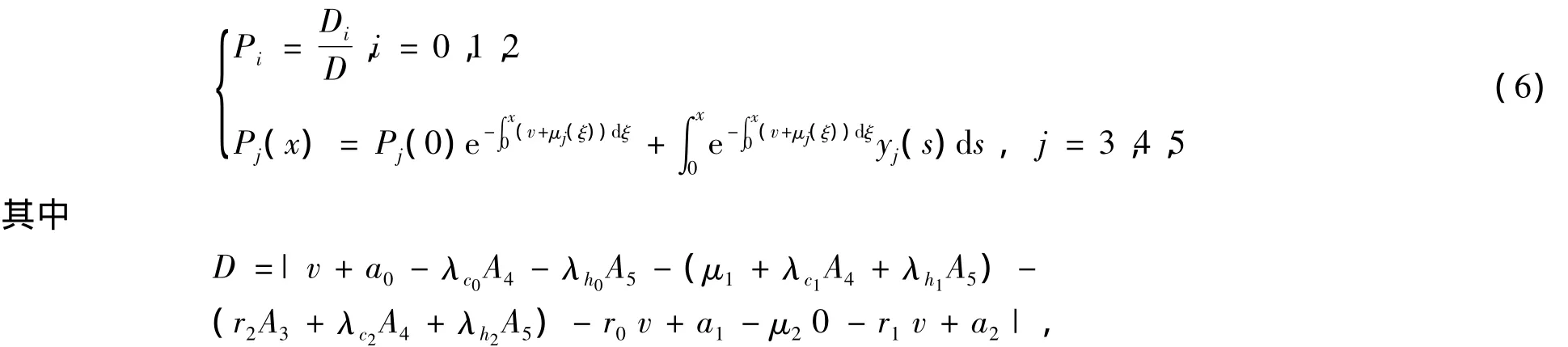
Di为以分别替换D中第k列所得行列式(k=1，2，3).

从而

考虑

其中

分项计算

即

另一方面

综上

故当v＞0时，[vI－(A+E)]－1存在且‖[vI－(A+E)]－1‖≤，由方程[vI－(A+E)]=的解可知，当v＞0时，若→y为非负向量，则P→亦为非负向量，故[vI－(A+E)]－1为正算子，从而A+E为预解正算子.

定理6 A+E的共轭算子

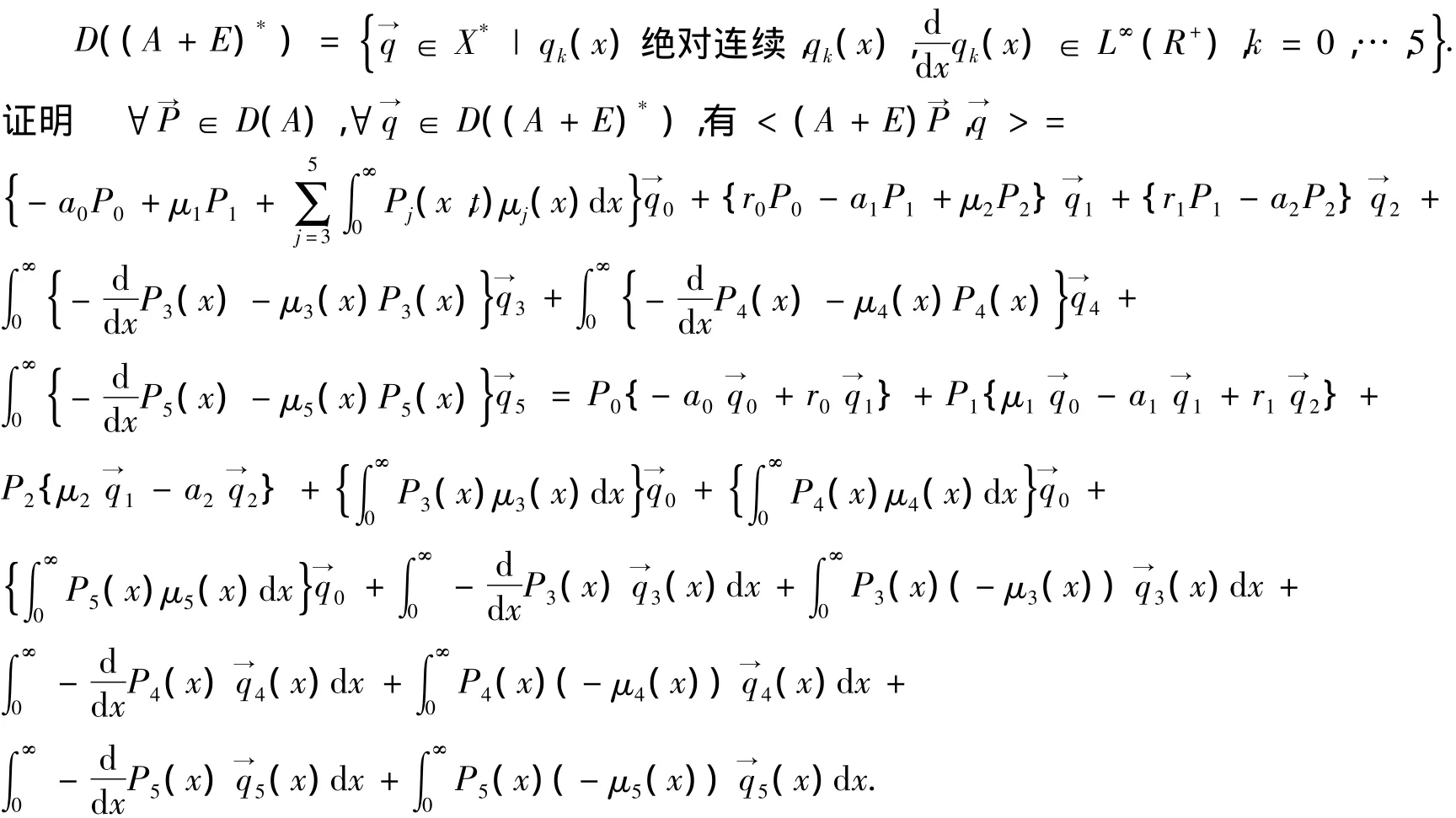
由于Pj(∞)=0，∈L1(R+)，则有Pj(∞)(∞)=0，则利用分部积分法，得到

下面分两个方面来证明:

一方面:若((A+E)*)定义域如上，即

成立，但此式成立的条件为:Pj(x)绝对连续，使得(x)几乎处处存在，(x)∈L1(R+)，使得

定理7 ω(A+E)=0.

证明由方程组移项得，

将方程组中各式对x从零到正无穷大积分，代入边值条件再相加，可，故方程组(7)～(10)

所对应的半群是非扩张半群，由A.Pazy[2]知‖T(t)‖=1，故半群的增长界ω(A+E)=0.

定理8 s(A+E)=0.

任取

则有

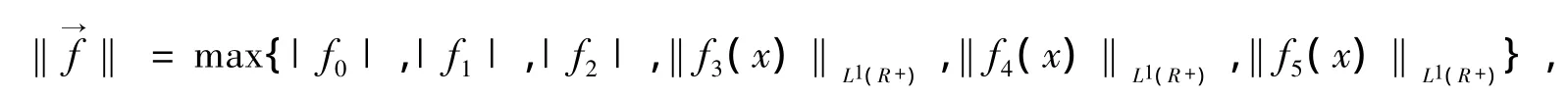
故

[1] Yang N F，Dhillon B S.Availability analysis of a repairable standby human-machine system[J]Microelectron Reliab，1995，35:1401-1413.

[2] Pazy A.Semigroups of Linear Operators and Applications to Partial Differ[M].Spring verlag Berlin Heidelbery:New York.

[3] 曹晋华，程侃.可靠性数学引论[M].北京:科学出版社，1986.

[4] 夏道行，吴卓人，严绍宗，等.实变函数论与泛函分析[M].北京:高等教育出版社.

[5] 方明，韩筱爽.一类具有可修复储备部件的人-机系统的解的存在唯一性[J].延边大学学报:自然科学版，2008，34(1):14-17.

[6] 姜英秀，韩筱爽.一类具有可修复储备部件的人-机系统解的指数稳定性[J].延边大学学报:自然科学版，2012，38(2):108-111.

[7] 方明，韩筱爽.一类具有可修复储备部件的人-机系统的解的谱特性[J].延边大学学报:自然科学版，2009，35(4):305-308.

[8] Arendt W.Resolvent Positive Operators[J].Proc London Math Soc，1987，54(3):321－349.