Heisernberg群上低阶特征值的估计
杨贵诚,杜锋
(1.湖北工业大学商贸学院基础课部,湖北武汉430079;2.荆楚理工学院数理学院,湖北荆门448000)
0 引言及主要定理
在一个(2n+1)维的欧氏空间RR2n+1上定义下列不可交换的群运算:

其中x,y,x′,y′∈RRn,t,t′∈RR;〈,〉RRn表示RRn上的内积.具有这种群运算的(2n+1)维欧氏空间RR2n+1称为Heisenberg群,记为HHn.而HHn上李代数HHn的基为

关于上述向量场,满足[Yp,Xq]=Tδpq,p,q=1,2,…,n.在Heisenberg群HHn上有如下定义的次椭圆算子

其中divHH,HH分别称为水平散度和水平梯度.ΔHH叫做Heisenberg群HHn上的Kohn Laplacian算子.设Ω是HHn上的有界区域,而∂Ω是Ω的边界,则当f|∂Ω=g|∂Ω=0,则有
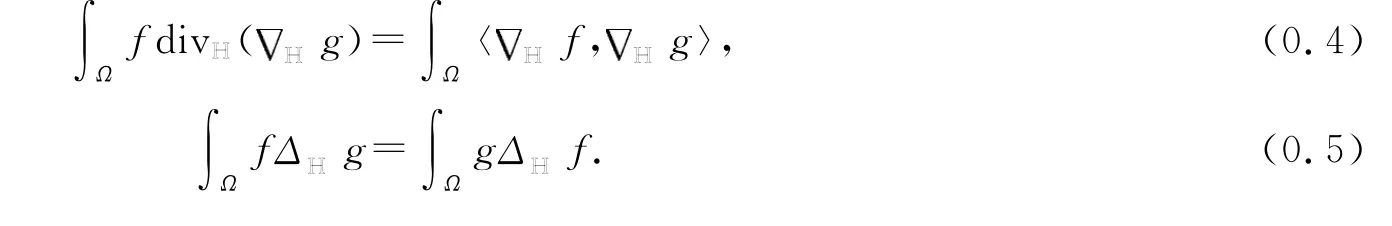
关于Heisenberg群上的特征值问题的研究已经有了许多成果,如文献[2-6].接下来,我们考虑Kohn Laplacian算子ΔHH的Dirichlet特征值问题:

我们知道其具有离散的谱.2009年,El Soufi等[6]证明了不等式

而在本文中我们将给出特征值问题(0.6)式的低阶特征值估计,关于各类流形及算子的低阶特征值的估计也有许多成果,如文献[7]等.而在本文中,我们得到下述定理
定理0.1 设Ω是HHn上的有界区域,λi是特征值问题(0.6)的第i个特征值,而ui是与之对应的正交特征函数,即有:

可得不等式:

注记:由(0.9)式容易得到

特别地,如n=1,则2λ2≤λ3+λ2≤6λ1可得
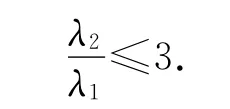
由此,我们可以得到一个与欧氏空间RRn上Dirichlet特征值问题相应的结论[1].
1 主要定理的证明
我们将给出本文中主要定理的证明,使用的一些符号与计算,具体细节可参看文献[2-3].
定理0.1的证明 为方便证明,我们令Yp=Xn+p,yp=xn+p,p=1,…,n,可得

定义一个2n×2n矩形C:=(Cαβ),这里
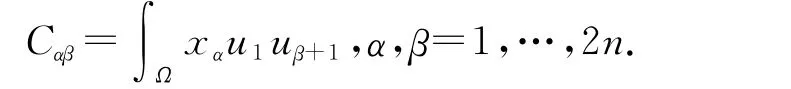
由Gram-Schimidt正交化分解可知,存在着一个2n×2n的上三角矩形阵R=(Rαβ)和一个2n×2n正交矩形阵T=(Tαβ),使得
因此,可得



和

令

可得

那么由Rayleigh-Ritz不等式,可以得到

这里

因此,由(1.4~1.6)式,我们有

而另一方面


这说明综合(1.8)式和(1.9)式,我们有

而


这说明

这里{δα}2nα=1是一族任意常数.
由此可知如果λα+1-λ1=0,显然可知

如果λα+1-λ1>0,令也可得到

再由(1.10)式,我们可得

在(1.12)式中对α由1到2n求和,再由(1.6)式,可得

由此可得(1.9)式,定理得证.
[1]Ashbaugh M S.Isoperimeteic and unversal inequalities for eigenvaluse//Davies,E B,Safarov Y,eds.Spectral Theory and Geometry[C].vol 273.Edinburgh:London Math Soc Lecture Notes,1999:95-139.
[2]Candidato D V,Relatore L A.Submanifolds in Cannot groups[M].Corso di Perfezionmento in Mathematica Triennio,2004.
[3]杜锋,吴传喜,李光汉.Heisenberg群上具有散度形式椭圆算子的特征值估计[J].数学物理学报,2012,30A(6):1032-1040.
[4]Huang G Y,Chen W Y.Inequalities of eigenvalues for Bi-Kohn Laplacian on Heisenberg group[J].ActaMath Sci,2010,30B(1):125-131.
[5]Niu P C,Zhang H Q.Payne-pólya-Weinberger type inequalities for eigenvalues of nonelliptic operators[J].Pacific J Math,2003,208:325-345.
[6]El Soufi A,Harrell E M,Ilias S.Universal inequalities for the eigenvalues of Laplace and Schrödinger operators on submanifolds[J].Amer Math Soc,2009,361(5):2337-2350.
[7]Sun H J.Universal inequalities and bounds for weighted eigenvalues of the Schrödinger operator on the Heisenberg group[J].Turk J Math,2010,34:1-10.

