无需参考信号的单晶炉温度干扰抑制新方法

张新雨，刘丁，梁军利，汪姣，杨文

(西安理工大学 自动化与信息工程学院，陕西 西安 710048)

单晶炉是利用直拉法生产集成电路硅材料的重要设备。在其直拉单晶硅的工作过程中，热是根本驱动力，影响着单晶硅的整个生长过程。随着集成电路线距达到低纳米级，对单晶炉固液界面处的温度检测与控制提出更为苛刻的要求，因为温度发生细微的波动都会导致晶体发生位错而造成拉晶失败[1-2]。然而在单晶炉的工作过程中，坩埚转动、加热器纹波、晶体转动等变化都会使得热场温度测量值存在周期性低频干扰，较高精度的温度控制变得较为困难。因此，如何在存在多个周期性低频干扰的情况下，对单晶炉热场温度测量值中的干扰实现抑制以达到热场温度控制系统的需求，就显得极为关键了。

目前，国内外大部分单晶炉采用红外传感器检测热场温度，然后运用中值滤波、均值滤波等工程方法进行处理，这些方法虽对温度测量值中的干扰具有一定抑制作用，但要满足高精度的控制仍存在不足，检测精度偏低，结果仍具有一定弱周期性。近年来，国内学者对单晶炉热场温度测量数据进行了研究分析，发现单晶炉热场温度测量值中存在多个周期性的低频干扰[3]。自适应滤波方法能够抑制干扰，但如何确定自适应滤波器的参考信号是一个重要问题[4]。目前，自适应滤波器的参考信号主要有两种[5-10]：一种采用正弦信号，即自适应陷波器，能够针对某一固定频率的干扰进行抑制，但需要已知干扰频率[5-6]；另一种采用与干扰相关的函数，即自适应对消法[7]，利用自适应算法根据参考信号抵消干扰[3,8-10]。以上方法均需要给定参考信号，但在实际应用过程中，会存在以下问题：

1)参考信号需要额外给定，一般很难准确获得；

2)在实际的工作环境中，由于条件限制，很难布置测量参考信号的传感器；

3)在测量参考信号的实际过程中，传感器难以仅采集到参考信号(例如干扰)，往往还包含了部分有用信号(例如温度)，因此在对消时，有用信号很容易被当作干扰对消掉。

近几年，迭代自适应法(iterative adaptive approach, IAA)作为一种非参数化的谱估计方法被提出[11]，为自适应对消法的发展提供了新的思路。该方法以其估计单个分量时不会被其它分量影响、幅值估计精度高、可用于少量数据等优点，被广泛应用于阵列信号处理[12]、水下通信[13]和图像处理[14]等领域。

为此，本文针对单晶炉热场温度测量值中存在多个周期性低频干扰的问题，提出了一种无需参考信号的新的自适应对消法。该方法将迭代自适应法引入自适应对消法中，直接利用迭代自适应法从输入信号中逐个获得低频干扰分量，然后将其消除。该方法相比传统的自适应对消法具有以下优点：1)当干扰为多个窄带干扰时，无需参考信号，降低了测量参考信号所需的硬件代价；2)估计每个干扰分量的过程中能够减小其它干扰分量的影响；3)迭代次数少。最后通过仿真和工程实验对该方法进行了有效性验证。实验结果表明，在实际的运行过程中，该方法在无需参考信号的条件下，对温度信号进行检测和处理时，能够有效地抑制单晶炉热场温度测量值中的干扰。

1 问题描述

在单晶炉直拉单晶硅的过程中，炉膛内部高温、负压的环境导致无法对整个热场进行测量。因此，一般采用红外传感器通过炉壁开孔获得固液界面平面处加热器的温度，进而间接获得热场温度，用于单晶炉的热场温度控制。单晶炉热场温度测量原理如图1所示。

图1 单晶炉热场温度测量示意图

直拉单晶硅的过程中，热场温度信号变化较为缓慢。由于坩埚转动、晶体转动、加热器电源纹波等都是周期性的干扰，加之红外传感器本身的测量噪声，因此，温度传感器获得的测量值不能直接用于单晶炉热场温度控制系统，需要对上述干扰进行滤波。根据上述分析，温度传感器获得的测量值可以写成：

(1)

式中，y(n)为传感器测量得到的温度信号，x(n)为缓慢变化的实际温度信号，ωi为干扰频率，ai和bi为干扰幅值，Δt为采样周期，k为低频干扰个数,v(n)为测量噪声，根据检测理论[15]和实验证明，v(n)近似服从高斯分布。

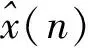
2 新的自适应对消法及单晶炉热场温度干扰抑制

2.1 建 模

设传感器测量的N个数据组成一个观察序列，则令:

由于一个频率分量对应一对正弦和余弦，因此，现将每一个频率分量所对应正弦和余弦的幅值定义为一个列向量，即:

αi=[a(ωi),b(ωi)]T

将ci和si写成一个矩阵Di=[ci,si]，由此，式(1)可以重写为:

(2)

2.2 自适应对消法原理

本文最终的目的是从y中估计x，然而，ωi、αi、Di、k和v均为未知，直接从y中估计x极为困难，因此，需采用自适应对消法的思想，通过估计ωi、αi、Di、k得到干扰，然后从y中将其消除，从而得到x的估计值。传统的自适应对消法如图2所示[7]，自适应对消器具有两个输入通道，一个为信号通道，即同时含有有用信号和干扰，一个为参考通道，主要为与干扰相关的函数。参考信号经过自适应算法运算后，送入自适应对消器，最后将其从信号源中消除。

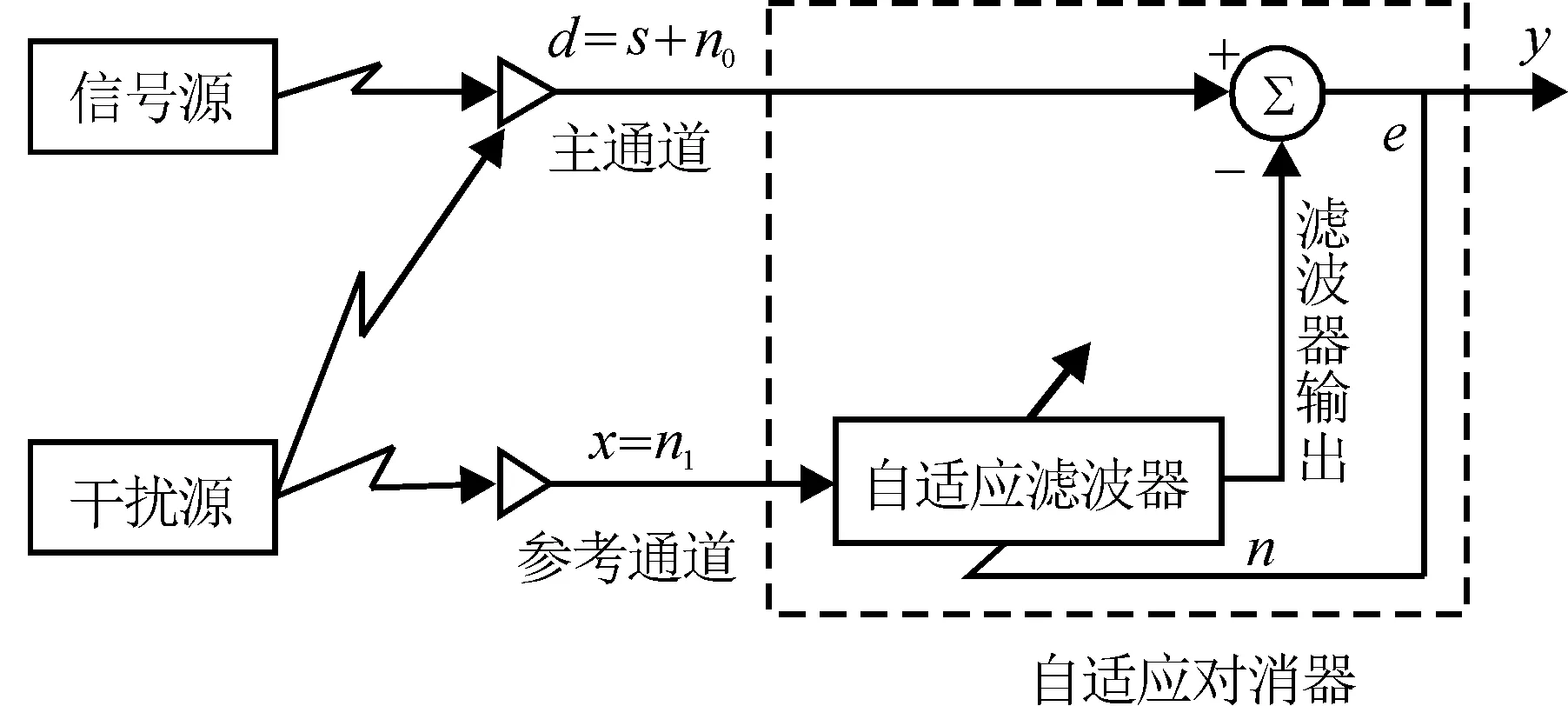
图2 传统自适应对消法框图

尽管传统的自适应对消法理论较为完备，但是参考信号一般需要额外测量。在单晶炉工作过程中，这些周期性干扰源难以确定，且炉膛内部负压、高温的环境，较难布置测量参考信号的传感器，因此，采用传统的自适应对消法抑制干扰较为困难。

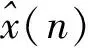
图3 本文自适应对消法框图

由图2和图3可以得出，与传统的自适应对消法相比，本文方法具有以下优点：1)无需参考信号，可以减小测量参考信号的硬件代价；2)在估计每个干扰分量的过程中，可以避免各分量之间相互影响，具有较高的估计精度和鲁棒性。

2.3 基于自适应迭代的对消法

设定干扰频率范围为[ωmin,ωmax]，生成一个虚拟的频率网格[11]。频率网格间距为Δω，则生成网格数量为:

(3)

通常y中含有多个频率分量，为避免其它分量的影响，迭代自适应法采用对每个频率分量逐个求解的思想，即求解某个频率分量时，其它分量都被看作噪声。因此，迭代过程中选用加权最小二乘法对目标函数进行求解。根据加权最小二乘法，目标函数可写为:

式中，Qj是求解第j个频率分量时所对应的协方差矩阵[16]。

(4)

(5)

(6)

根据加权最小二乘法，可得:

(7)

根据矩阵求逆引理[17]得:

(8)

3.2 康复医学促进社会融合 残疾人、老年人和其他功能障碍者的社会参与能力不同程度受限，通过康复医学的有效干预，可以促进残疾人的社会融合。康复医疗强调的是通过功能训练和必要的辅助措施，改善其功能。通过康复治疗改善患者的自理能力，减轻家庭和社会负担，提高生活质量，并能使患者早日回归社会。康复医学近年也在秉承国际社会倡导的全人发展的理念，在提高个体功能水平的同时，越来越多地关注康复服务对象获得医疗康复服务后的社会参与、机会均等、权利保障等问题。

将上式代入式(7)得:

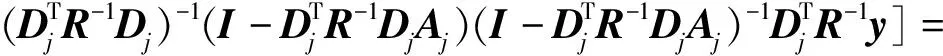
(9)

根据上述推导过程，式(9)相对式(7)省略了求Qj的步骤，由式(4)和式(5)及算法复杂度计算可得，在一次迭代过程中复杂度上限降低了O(N3)。

第j个频率对应的功率为[16]:

(10)

依次计算m个频率对应的功率，然后迭代10～20次[16]，最后在P(ωj)(j=1,2,…,m)中选取大于设定阈值为PTH的所有峰值，则峰值个数为干扰个数k，对应的频率ωj和幅值αj=[a(ωj),b(ωj)]T为干扰的频率和幅值，最后从y中将干扰消除。

2.4 算法步骤详述

本文所提算法步骤如下。

1)设置算法初始参数：频率范围为[ωmin,ωmax]，频率网格间距为Δω，最大迭代次数为L，功率阈值为PTH；

4)判断迭代次数是否大于L，如果大于L，转到步骤 5)，否则转到步骤 3)；

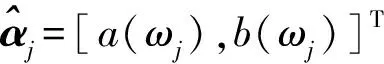
3 实验结果与分析

为验证本文方法的有效性，本文应用上述算法处理以下数据：1)仿真数据；2)单晶炉热场温度检测工程实验测量数据。在对单个观察序列进行实验时与经典的匹配滤波和傅里叶变换进行比较，对多个观察序列进行滑动估计实验时与经典的中值滤波和基于粒子群搜索幅值的自适应抵消法(文献[3]方法)进行比较。

3.1 仿真实验

本次实验利用下式产生三组仿真数据:

设置IAA算法初始参数，观察序列数据长度N=64，频率范围为fmin=0.01 Hz，fmax=0.49 Hz,频率网格间距为Δf=0.000 1 Hz，最大迭代次数L=18，功率阈值为PTH=1。

在信噪比为23、29和31的情况下，对某个观察序列进行500次蒙特卡洛实验，并且与匹配滤波(匹配频率选择0.01～0.49 Hz)、傅里叶变换进行了比较，图4～6分别为500次实验平均之后的归一化非参数化估计谱，由图4～6可得，与匹配滤波和傅里叶变换相比，本文方法在估计每个干扰分量的时候并不会受到其它分量的影响，具有较强的旁瓣抑制能力，峰值较尖，对频率估计的分辨率较高。而匹配滤波与傅里叶变换的结果由于各个分量之间影响较大，峰值较多。由上述可得，本文方法在不同的信噪比下能够准确地搜索到信号的非参数谱的峰值，进而得到低频干扰的频率和幅值，并且500次实验结果基本一致，具有较强的鲁棒性、稳定性和旁瓣抑制能力。

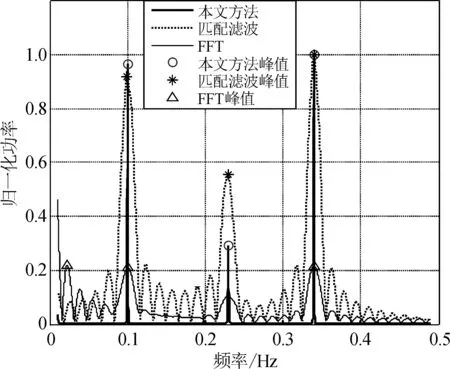
图4 实验一μ=23时非参数化谱估计结果

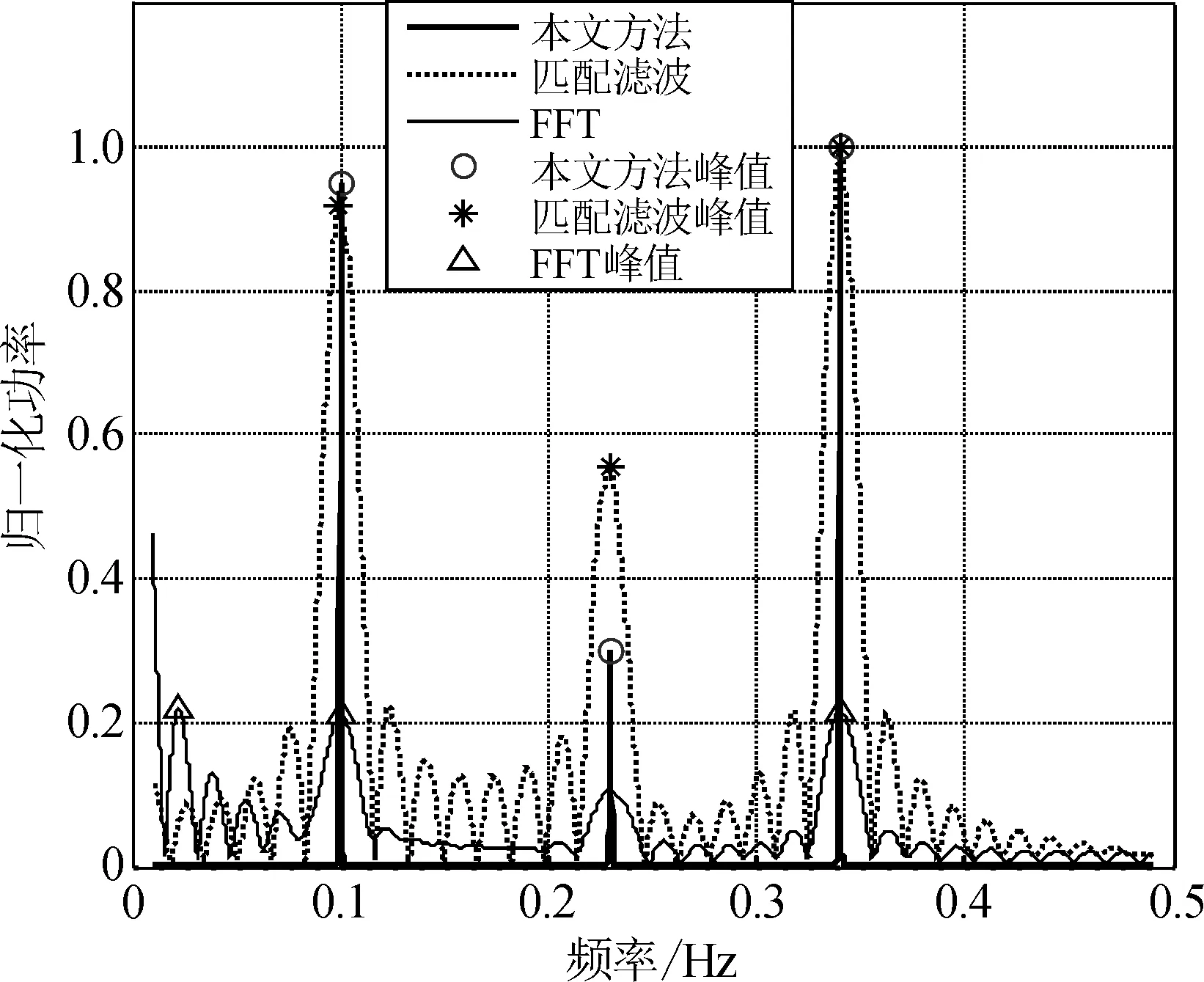
图5 实验一μ=29时非参数化谱估计结果

图6 实验一μ=31时非参数化谱估计结果

为更清晰地观察本文方法对频率、幅值以及对消后所得有效信号的估计误差，现定义如下均方误差(mean-square error，MSE):

其中ξ分别取f1,f2,f3,Ψ1,Ψ2,Ψ3,x。

表1为在三种信噪比下对频率、幅值估计值以及对消后所得信号500次实验的MSE。由表1可得，本文方法对频率和幅值估计具有较高的精度，并且估计精度随着信噪比的提高而提高。同时，本文方法能够有效地抑制周期性干扰(稳定在±0.1内)。

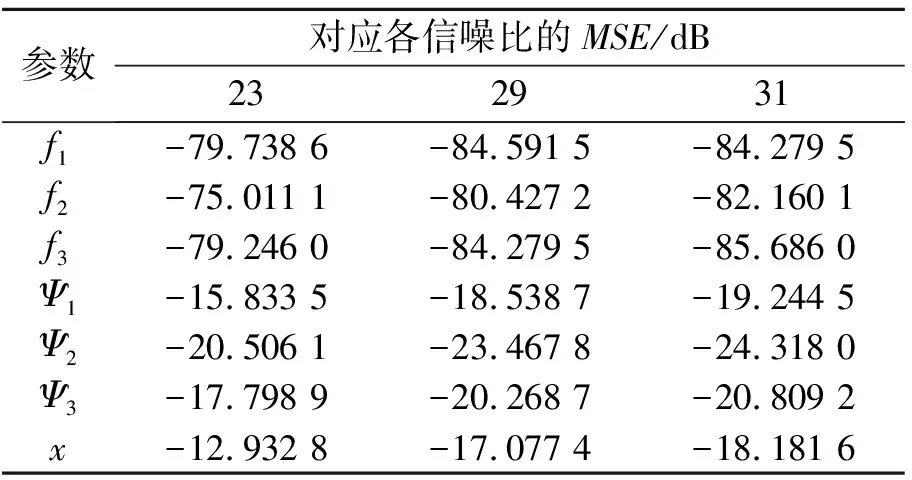
表1 实验一本文算法检测结果的MSE

图7～9分别为中值滤波、文献[3]方法和本文方法在信噪比为23、29和31时对200个数据点进行滑动滤波的结果。由图可得，在不同信噪比下，本文方法的滤波效果明显优于均值滤波，并且在无需参考信号的条件下，略优于文献[3]方法(需要已知参考信号的频率)。

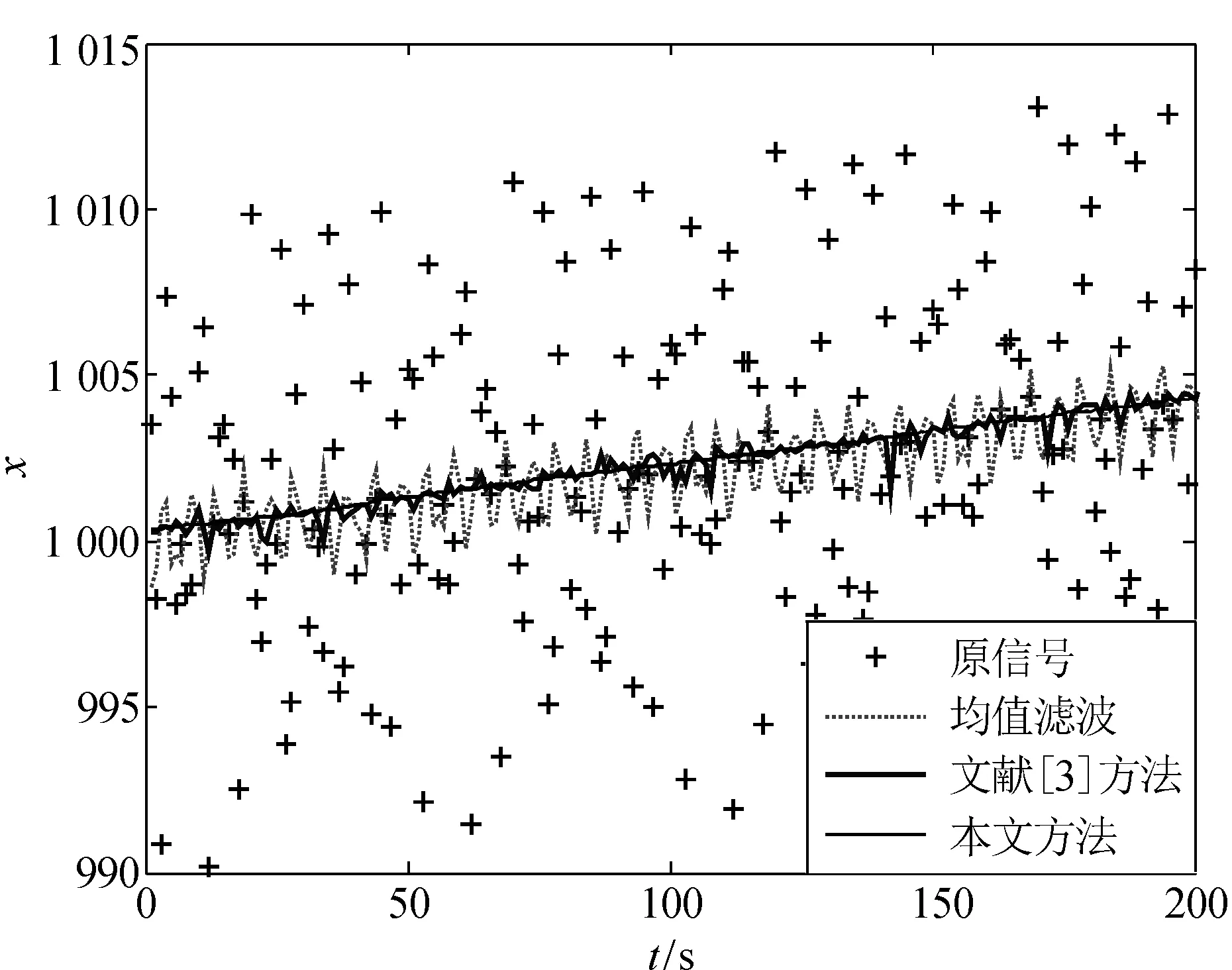
图7 实验一μ=23时不同方法滤波结果

图8 实验一μ=29时不同方法滤波结果

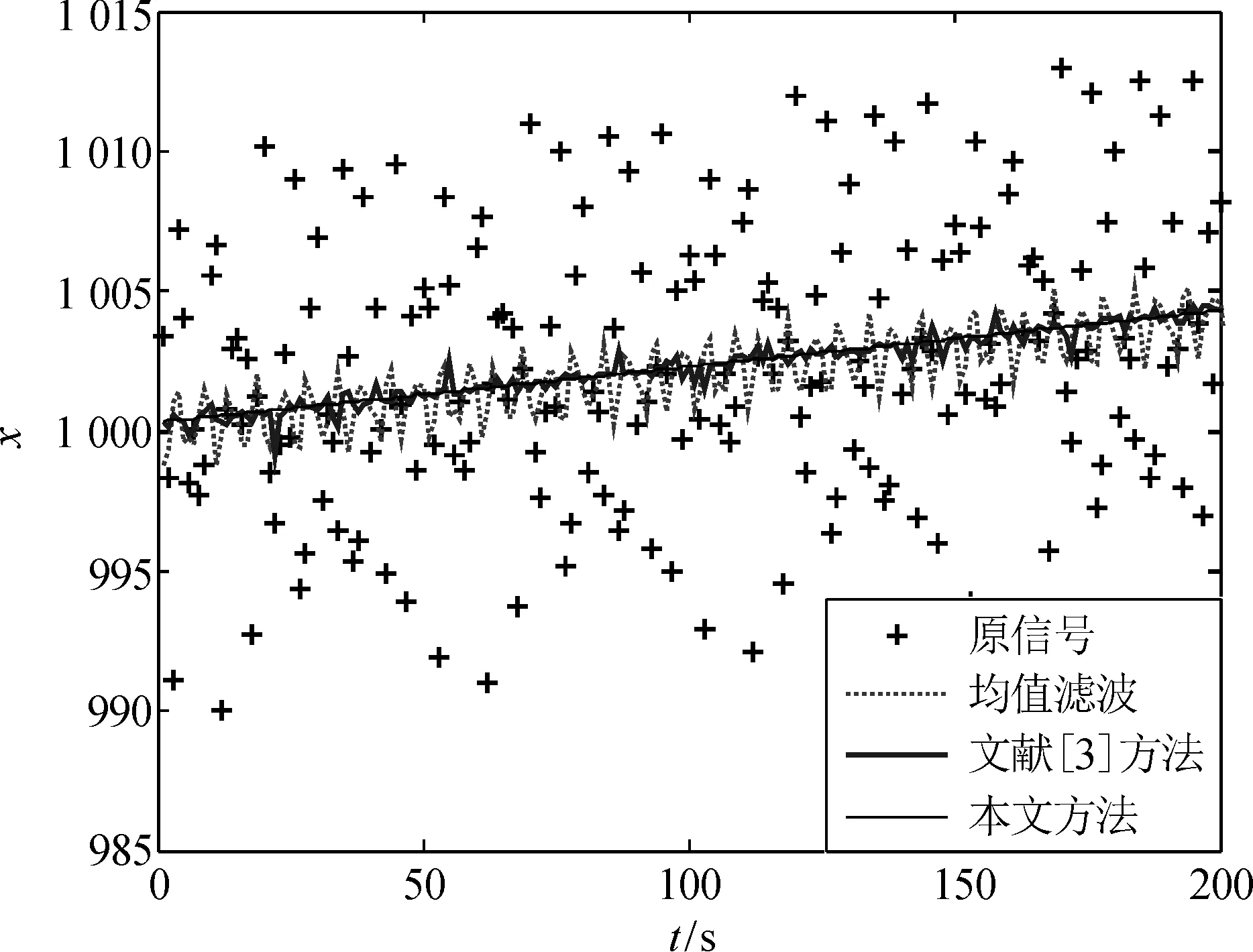
图9 实验一μ=31时不同方法滤波结果

3.2 单晶炉热场温度工程检测实验

3.2.1 实验准备

本次实验依托TDR-150型单晶炉进行，TDR-150型单晶炉为极大规模集成电路所用单晶硅的全自动生长设备，投料量为170 kg，控制直径为300 mm，等径长度为650 mm，TDR-150型单晶炉和温度传感器如图10所示。

图10 TDR-150型单晶炉及温度传感器

根据单晶炉热场温度先验信息设置参数：频率范围为fmin=0.1 Hz，fmax=4.9 Hz,频率网格间距为Δf=0.001 Hz，采样时间为Δt=0.1 s，功率阈值PTH=1，其余参数设置均与实验一相同。

3.2.2 实验结果及分析

图11为对250个数据点进行滑动估计的平均非参数化谱(进行归一化之后与匹配滤波、傅里叶变换进行了比较)，由图11可知，本文方法能够准确地搜索到非参数化估计谱的峰值所对应的干扰频率，并且在估计某个干扰分量时能够减小其它分量对其的影响，对旁瓣具有较强的抑制能力，且峰值比较尖，具有较高的分辨率。而匹配滤波和傅里叶变换由于估计每个分量时受其它分量干扰较大，不能准确搜索到干扰频率所对应的峰值。因此，这两种方法不能提供有效的干扰进行对消。

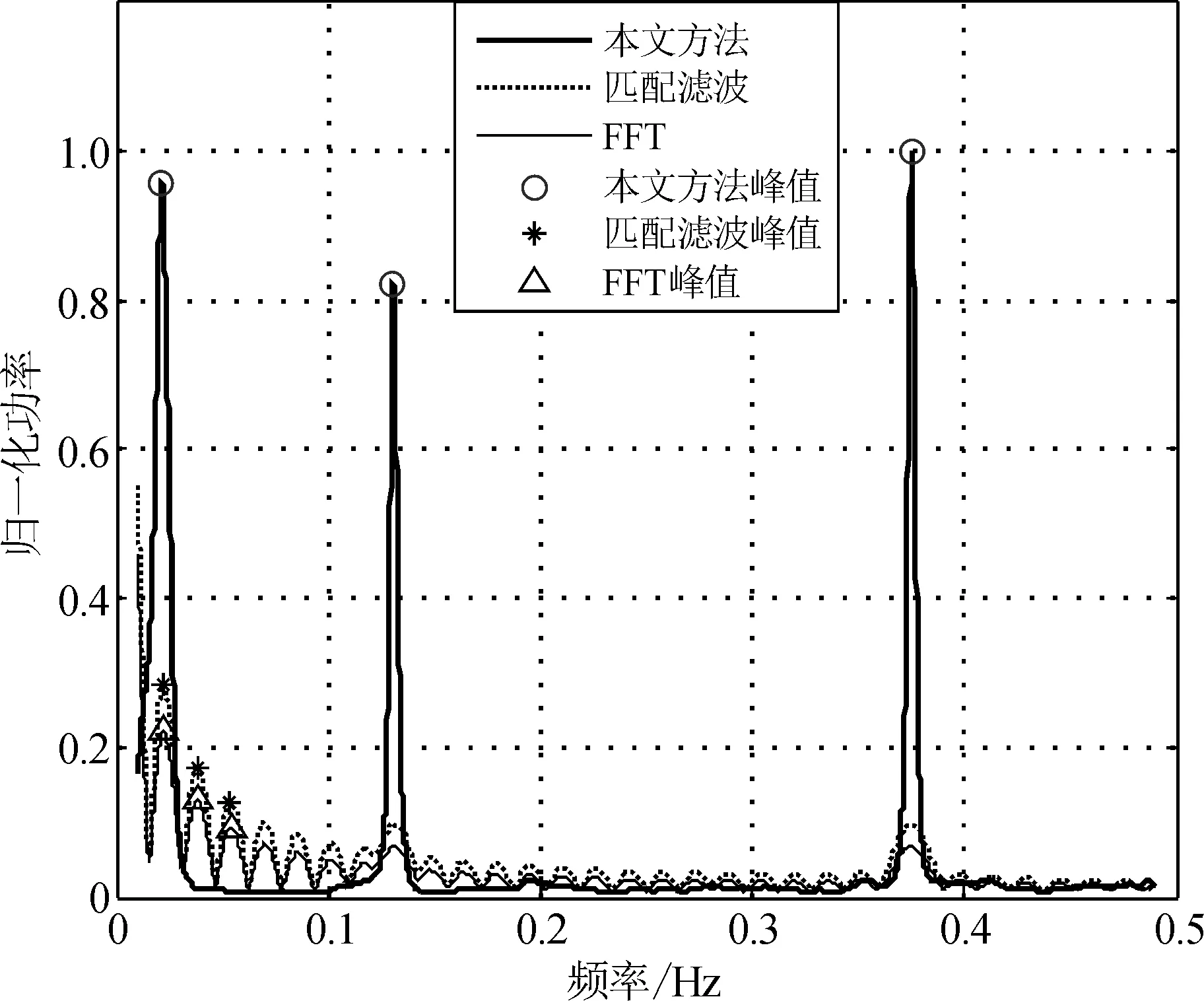
图11 实验二非参数化谱估计结果

图12为中值滤波、文献[3]方法和本文方法对250个数据点进行滑动滤波的结果。

根据图12可得，本文方法在没有参考信号的条件下，能够有效抑制单晶炉热场温度测量值中的干扰(在±0.3℃以内)，并且结果优于中值滤波和基于粒子群搜索幅值的对消法(干扰频率已知，滤波结果在±1℃内波动)，符合TDR-150型单晶炉热场温度控制系统的需求。

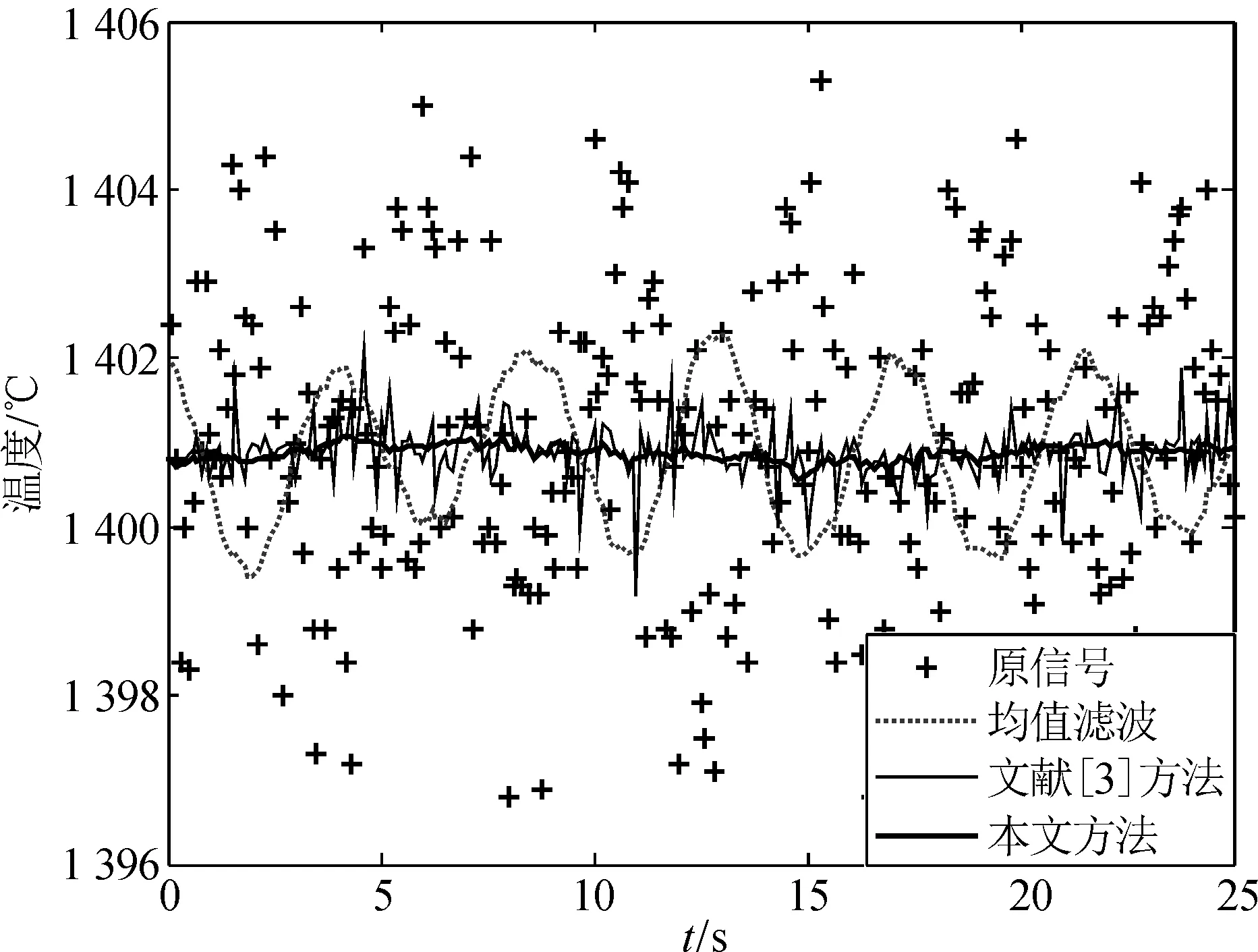
图12 实验二不同方法滤波结果

4 结 论

本文提出了一种无需参考信号的自适应对消法。该方法将迭代自适应法引入自适应对消法中，直接利用迭代自适应法从输入信号中逐个估计低频干扰分量，然后将各个干扰分量消除。仿真和工程实验表明，该方法在无需参考信号的条件下，能够准确估计各个干扰分量，从而有效地抑制单晶炉热场温度测量值中的干扰，优于现有方法，符合单晶炉热场温度控制系统的工艺要求。

参考文献：

[1] Fang H S, Jin Z L, Huang X M. Study and optimization of gas flow and temperature distribution in a Czochralski configuration[J]. Journal of Crystal Growth, 2012, 361: 114-120.

[2] 杨润，李淑娟，彭曦，等. 直拉式单晶炉动态性能分析与预测[J]. 西安理工大学学报, 2012,28(3):298-302.

Yang R, Li Shujuan, Peng X, et al. Dynamic characteristic analysis and prediction for CZ single crystal furnace[J].Journal of Xi'an University of Technology, 2012,28(3):298-302.

[3] 梁炎明, 刘丁, 赵跃. 基于自适应噪声抵消的 CZ 单晶炉炉膛温度信号处理[J]. 控制理论与应用, 2011, 28(1): 94-100.

Liang Y M, Liu D, Zhao Y. Temperature signal processing based on adaptive noise cancellation for CZ crystal growing furnace[J].Control Theory & Applications, 2011,28(1): 94-100.

[4] 西蒙·赫金. 自适应滤波器原理[M]. 第四版. 郑宝玉,译. 北京：电子工业出版社，2010: 15-17.

[5] McNamara D M, Ziarani A K, Ortmeyer T H. A new technique of measurement of nonstationary harmonics[J]. Power Delivery, IEEE Transactions on, 2007, 22(1): 387-395.

[6] 梁炎明, 刘丁, 任海鹏, 等. 基于自适应陷波的直拉单晶直径跟踪[J].仪器仪表学报, 2010, 31(7): 1441-1447.

Liang Y M, Liu D, Ren H P, et al. Diameter tracking in pulling of crystals based on adaptive notch filtering [J]. Chinese Journal of Scientific Instrument, 2010, 31(7): 1441-1447.

[7] 沈福民. 自适应信号处理[M].西安：西安电子科技大学出版社，2001: 136-147.

[8] Meng J E, Li Z R, Cai H N, et al. Adaptive noise cancellation using enhanced dynamic fuzzy neural networks[J].IEEE Transactions on Fuzzy Systems, 2005, 13(3): 331-341.

[9] Gorriz J M, Ramírez J, Cruces-Alvarez S, et al. A novel LMS algorithm applied to adaptive noise cancellation[J]. IEEE Signal Processing Letters, 2009, 16(1): 34-37.

[10] Allik B, Ilg M, Zurakowski R. Ballistic Roll Estimation using EKF Frequency Tracking and Adaptive Noise Cancellation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2546-2553.

[11] Yardibi T, Li J, Stoica P, et al. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 425-443.

[12] 汤小为, 朱伟, 汤俊. 基于自适应迭代的非参数化虚拟孔径合成方法[J].清华大学学报: 自然科学版, 2012, 52(9): 1265-1269.

Tang XW, Zhu W, Tang J. Non-parametric algorithm for virtual aperture synthesis based on the iterative adaptive approach[J].Tsinghua University(Sci & Tech), 2012, 52 (9): 1265-1269.

[13] Ling J, Yardibi T, Su X, et al. Enhanced channel estimation and symbol detection for high speed multi-input multi-output underwater acoustic communications[J].The Journal of the Acoustical Society of America, 2009, 125: 3067-3078.

[14] Roberts W, Stoica P, Li J, et al. Iterative adaptive approaches to MIMO radar imaging[J].IEEE Journal of Selected Topics in Signal Processing, 2010, 4(1): 5-20.

[15] 周杏鹏. 传感器与检测技术[M].北京：清华大学出版社, 2010: 24-30.

[16] Stoica P, Li J, He H. Spectral analysis of nonuniformly sampled data: a new approach versus the periodogram[J]. IEEE Transactions on Signal Processing, 2009, 57(3): 843-858.

[17] 张贤达. 矩阵分析与应用[M].北京：清华大学出版社, 2004: 68-69.