河口底边界层湍流信号的噪声干扰实验*

叶智豪，刘 欢

(中山大学海洋学院∥近岸海洋科学与技术研究中心，广东 广州 510275)

湍流是一种不规则运动，其流场的各种特征量是时间和空间的随机变量[1]。正因为如此，我们很难通过时间或者空间的函数对湍流的细节进行描述。但又因为湍流具有随机性，因此可以运用统计规律，对其速度、温度、压强、切应力等特征量进行统计上的描述。目前，在对河口湍流所进行的研究中，ADV(Acoustic Doppler Velocimetry)是应用最广泛和最有效的观测工具之一[2-3]。在河口的实际观测中，ADV的测量信号往往会受到水体气泡、大颗粒悬浮物、边界回声和边界几何结构等因素的影响，使得测量信号的相关系数和信噪比降低[4-5]。另一方面，潮汐、波浪等外部动力因素的干扰，也会给湍流信号的分离带来一定的困难[6]。由于ADV所测得的原始湍流数据可能混入了其他噪声等的信息，因此许多学者对湍流数据的后处理开展了研究。Goring和Nokia[4]首次引入庞加莱映射思想，提出了相空间临界值法去除数据中的毛刺点。对湍流信号中噪声的处理必然涉及两个问题，一是判断方法中阈值选取对噪点判断的影响，二是对噪点的合理替代。Wahl[7]对相空间法进行了改进，提出根据最大绝对期望中值而非标准差作为判断噪点的阈值。Parsheh等[8]则指出利用最近有效值点替代毛刺点更为合理。此外，Chanson等[9]较为详细地总结了现场观测中湍流信号的后处理流程，对比了不同后处理方法对湍流数据的影响。在前人工作的基础上，作者所在课题组也对湍流数据的后处理进行了探讨[10]，提出了一套关于湍流后处理的综合技术方法，指出后处理对平均流速影响不大，但会显著改变脉动流速统计分布特性，未经处理的原始数据不适宜用于分析湍流特征量[11]。

尽管如此，对于湍流信号的处理中，仍有2个问题值得思考：① 如何从实际测量得到的原始数据中识别湍流信号？② 当湍流信号混入其他干扰噪声后，对湍流信号会造成何种影响？目前针对河口底边界层湍流数据的后处理大多集中在滤波和去噪两个环节，讨论了不同后处理方法之间的差异，但对于不同类型噪声对湍流信号所造成的影响研究不多。详细探讨湍流信号的噪声干扰效应，有助于更好地区分湍流和其他类型信号之间的差异，深化对湍流本质的认识。在河口底边界层中，有3类较为典型的噪声，分别是高斯白噪声、趋势项和周期项，基于珠江河口黄茅海水域底边界层的湍流现场观测资料，本文将通过设置几组数据实验，对以上3类噪声对湍流信号的干扰效应问题进行探讨。

1 数据来源

2007年7月17-22日，中山大学海洋中心于珠江口崖门附近进行了4个测次，每个测次25 h的定点连续观测，本文选用位于崖门水道顺直处的YM03站的观测资料进行分析，因为该测站在4个测次中受河口外部动力因素(层化、风浪、弯道环流)的影响最小(图1a)。观测方式为座底式平台观测，其中，对湍流的观测所使用仪器为Nortek公司生产的三维点式流速仪ADV，探头距底25 cm，测点距底约为10 cm，采样频率为64 Hz，采样周期为每900 s观测300 s[12]。

座底三脚架上的CTD资料显示，观测期间YM03近底层的盐度约为0.2‰，基本不受密度层化的影响。风速仪的资料显示，YM03风速均值约为2.7±5.1 m/s，风向在180°～270°之间。由于受河道地形的限制，观测站位水流主要表现为往复流特征，且风浪作用不明显。从水面高度和近底平均流速(图1b、c)在潮内的变化可以看出，崖门水道主要受不规则半日分潮M2分潮的影响，涨落潮不对称性显著。当近底平均流速较大时，平均流对数剖面的拟合相关系数较好，且湍流3个方向的脉动强度较为接近，湍流各向同性满足最好；而在憩流时刻，垂向脉动明显小于其他两个方向，湍流各向异性增强[13-14]。因此本文选择涨急时刻的资料进行分析，该时段平均流速约为0.5 m/s(图1b、c虚线所示)。

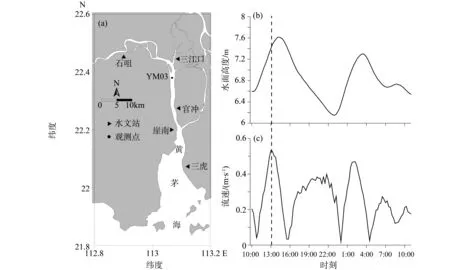
图1 观测站位和2007年7月20日水深、流速过程线Fig.1 Sketch map for the site of the survey station and variation of water depth and velocity on 20th,July，2007

在三个方向上，垂向流速受波动的影响较之水平流速要小，垂向脉动流速w′主要由湍流产生[15]，因此本文选取涨急时刻垂向脉动流速作为背景湍流信号。为避免其他噪声和毛刺点的影响，对湍流数据也进行了滤波、去噪的后处理[16]。处理后的湍流数据如图2a所示，脉动速度值绝大部分分布在-0.1～0.1 m/s之间。背景湍流信号带有明显随机信号的特征，其概率分布为准正态分布，偏态系数和峰度系数分别为0.16和0.23(图2b)。湍流信号另一个重要的特征是其具有宽谱性，且在能谱上具有惯性副区，即在湍流能谱的某个波数范围内，能谱密度值只与湍动能耗散率和波数有关，而与湍流在大尺度的能量输入及在小尺度的能量耗散无关。对于充分发展的湍流边界层，湍流在大尺度的能量输入与在小尺度的粘性耗散处于平衡，其一维湍流能谱在惯性副区具有-5/3的斜率分布[17]。从所选取的湍流信号的能谱曲线(图2c)可以看出，该湍流信号较好地满足以上特征。

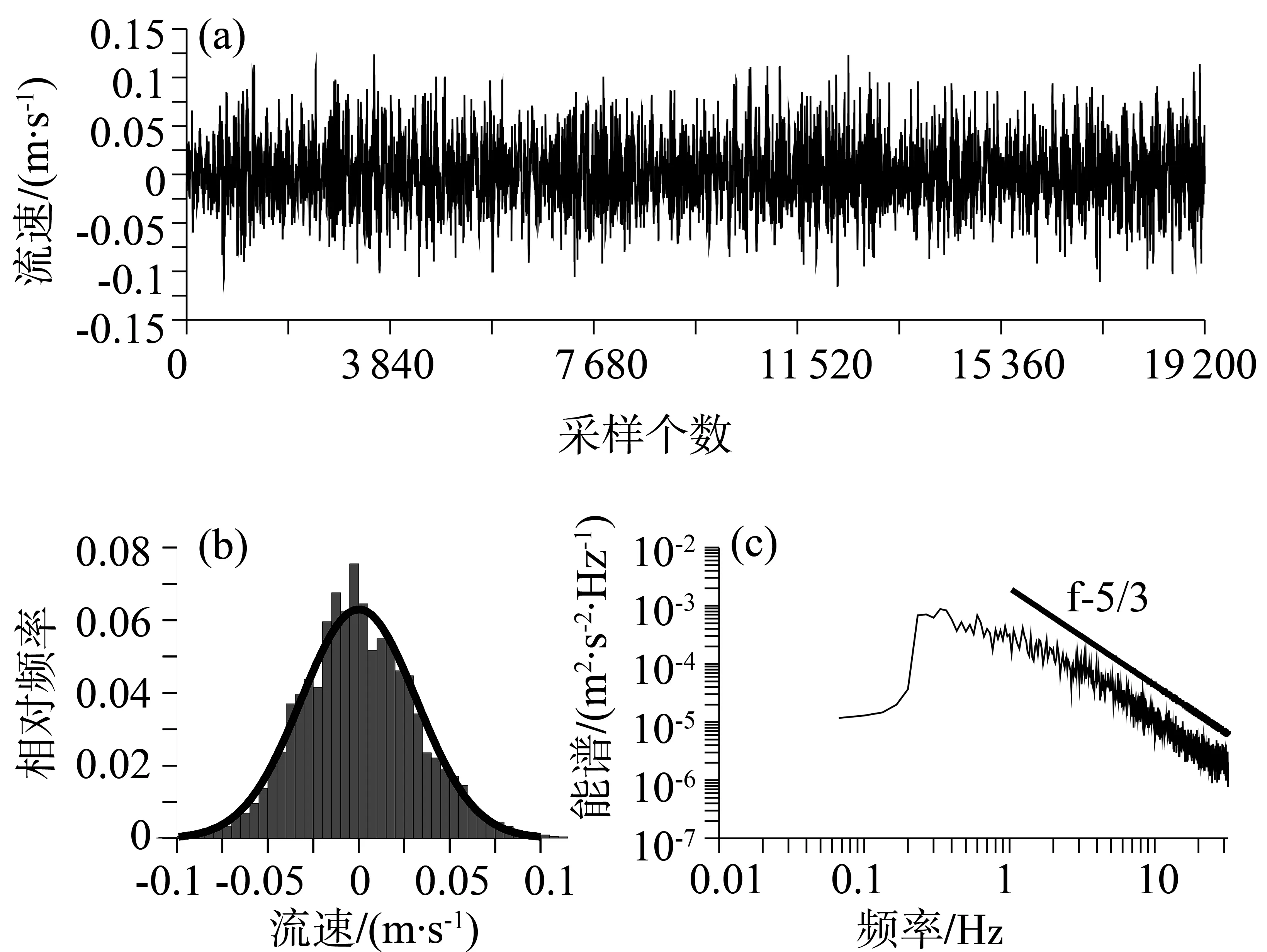
图2 背景湍流信号时间序列、概率分布和能谱Fig.2 Time series, probability distribution and energy spectra of the background turbulent signals

2 实验数据设置

为考察噪声对湍流信号的影响，本文主要考虑以下3种情况：① 高斯白噪声。高斯白噪声是一种具有正态分布概率密度函数的噪声，由于该噪声信号具有随机性，且其概率密度函数分布与湍流相似，因此选择此类噪声具有一定的代表性。在白噪声信号中，信号的标准差(噪声强度)是最重要的特征参数，设置高斯白噪声的噪声强度从0.005～0.05 m/s变化，其中第6组的噪声强度0.03 m/s与背景湍流强度0.031 2 m/s接近。② 趋势项。在河口中，水体流动带有明显的非定常性，尤其是在转流时刻，加速(或减速)效应对底边界层平均流和湍流结构均有重要影响[14,18]。以YM03为例，转流时刻的观测数据显示，5 min内流速的增量可达0.1 m/s(约为3.33×10-4m/s2)；而在整个涨潮加速段2 h内，水体的加速度约为6.67×10-4m/s2。在本文中，趋势项的设定仅考虑线性增加，截距均设为0，斜率范围在(3.33～66.7)×10-5m/s2之间。③ 周期项。波浪是河口湍流观测中一个重要的影响因素，通常而言，波浪的周期在100s这一量级。此外，船行波的扰动、涌浪的干扰等也可能会使观测到的湍流信号带有周期性的振动。潮汐的周期性变化因观测时段较短(每次采样持续时间为5 min)，可以认为其影响不大。本文的实验中，周期项周期的设置均小于20 s，振幅均设为0.03 m/s。对于以上3种情况，每种情况分别设置7组特征值，其中，各组背景湍流的湍强均为0.312 m/s，脉动能量均为0.001 m2/s2，能耗率5.64 W/kg；1-7组的高斯白噪声强度依次为0.005, 0.010, 0.015, 0.020, 0.025, 0.030, 0.050 m/s，趋势项斜率依次为0.333×10-4, 0.667×10-4, 1.330×10-4, 2.000×10-4, 2.670×10-4, 3.330×10-4, 6.670×10-4m2/s2, 周期项依次为0.2, 0.5, 1, 2, 5, 10, 20 s。

3 结果与讨论

3.1 概率分布

分别作出各组混入噪声后的湍流信号的概率分布，可以看出，混入噪声后的湍流信号仍基本满足正态分布(图3)。在高斯白噪声的实验中，随着噪声强度的逐渐增强，其概率分布渐趋平坦。混入趋势项后湍流信号的概率分布变化规律与混入高斯白噪声的类似，随着斜率的增大，数据出现在均值0附近的概率逐渐降低。周期项噪声对湍流信号概率分布的影响不大，各组数据的概率分布随着周期的变化不明显。

对于标准正态分布，其偏态系数和峰度系数均为0。统计各组数据的偏态系数和峰度系数随各自噪声特征参数的变化规律，可以看出，① 对于高斯白噪声，随着噪声强度的增大，分布越来越趋于标准的正态分布，当高斯白噪声的强度大于湍强时(噪声强度为0.05 m/s)，分布几乎完全符合正态分布(图4a)。这是由于噪声的信息已经完全掩盖了湍流的信息，导致混合后的信号特征主要受控于高斯白噪声。② 对于趋势项，偏态系数随着斜率的增大而逐渐减小，趋向于零。而峰度系数在斜率为2×10-4m/s2和2.67×10-4m/s2时最接近0，其后随着斜率的增大，峰度系数趋向负值，意味着逐渐偏离正态分布(图4b)。由前文的分析可知，河口底边界层中，转流时刻的加速度约为3.33×10-4m/s2，因此可以认为线性的趋势项对湍流的概率分布影响不大。③ 对于周期项，总体来看周期项使湍流信号更趋向于正态分布，混入周期项后湍流信号的偏态系数和峰度系数更接近于0(图4c)。由以上分析可以看出，测量数据的概率分布不足以说明数据中是否只含有湍流信号。当湍流混入其他噪声后，其概率分布仍可能满足正态分布，且混入噪声后的信号满足正态分布的程度可能较原始湍流信号更好。

3.2 能谱

当3类不同类型的噪声混入湍流信号后，它们对一维能谱的影响也有所不同。图5展示的是混入3类噪声后的湍流信号的能谱，限于篇幅，每类只抽取了3个特征值。可以看出，① 对于高斯白噪声，当噪声强度比湍流强度小1个数量级时，噪声对湍流能谱的影响不大，能谱曲线仍能较好地满足-5/3律。但当噪声强度和湍流强度相当时，会严重影响湍流的惯性子区，惯性子区带宽逐渐减小，甚至可能出现在高频区域内完全是噪声信息的情况(图5c)。在实际河口的观测中，憩流时刻流速较小，此时噪声对湍流能谱的影响较大(文献[14]中图5)。② 对于趋势项，本文设置的7组实验中，斜率的变化对能谱的影响均不大，不论是能谱值还是-5/3律的惯性子区带宽，均变化很小。这是由于文中设置的趋势项周期无限大，因此对频域上高频的信息影响较小。③ 对于周期项，从能谱曲线可以看出，周期项仅对相应周期所对应的频率有影响，出现明显的峰值。但对于湍流这样一种宽频信号而言，周期项对能谱中其余频带没影响，且对惯性子区的整体分布规律影响不明显。

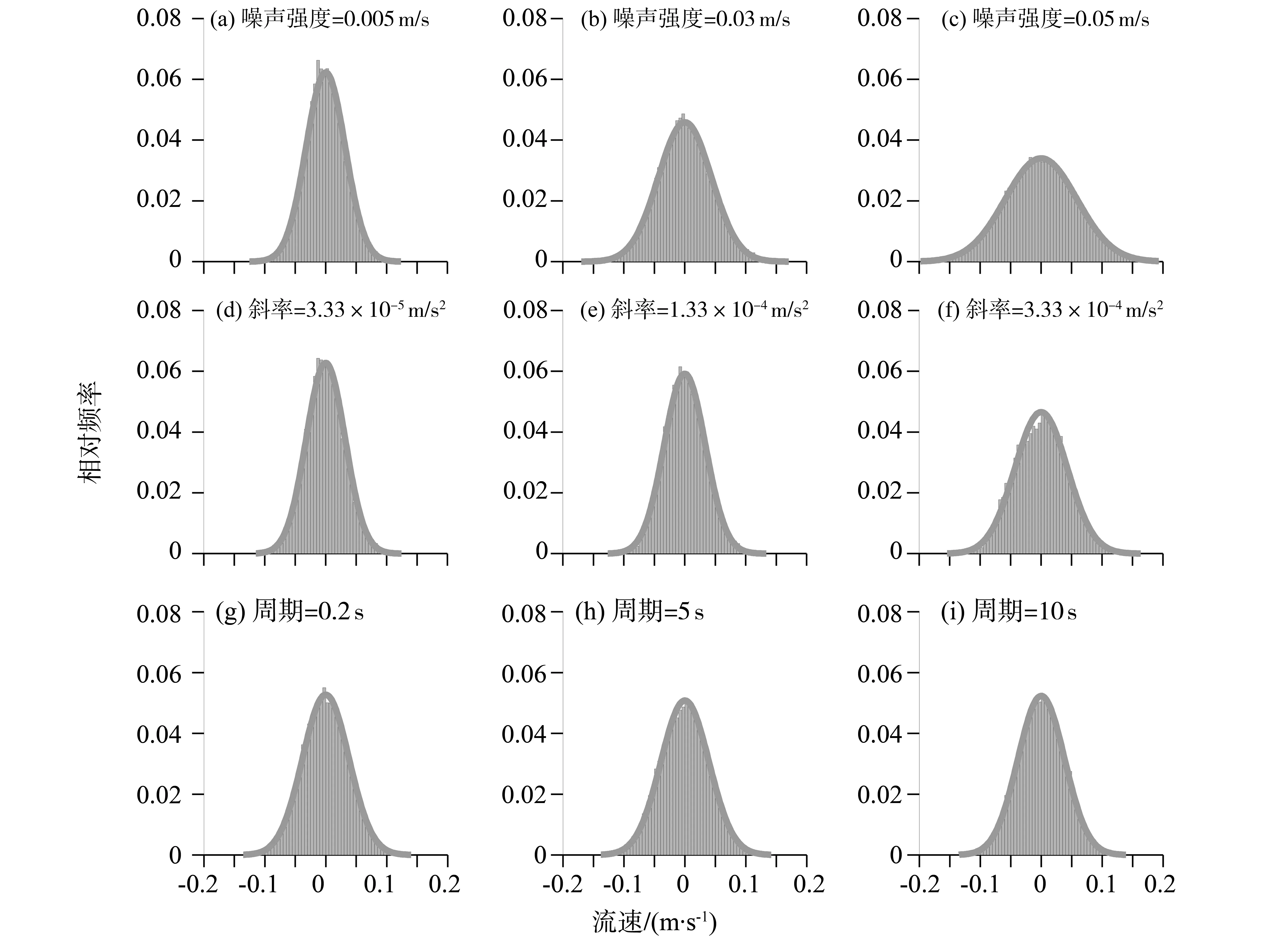
图3 混入不同噪声后湍流信号的概率分布Fig.3 Probability distribution of turbulent signals which contain different noises

3.3 湍动参数

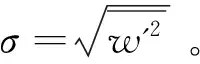
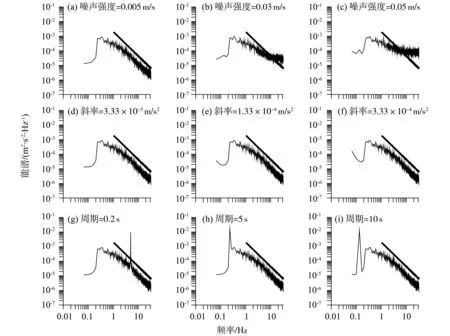
图5 能谱随噪声特征参数的变化Fig.5 Variation of energy spectra with noise characteristic parameters

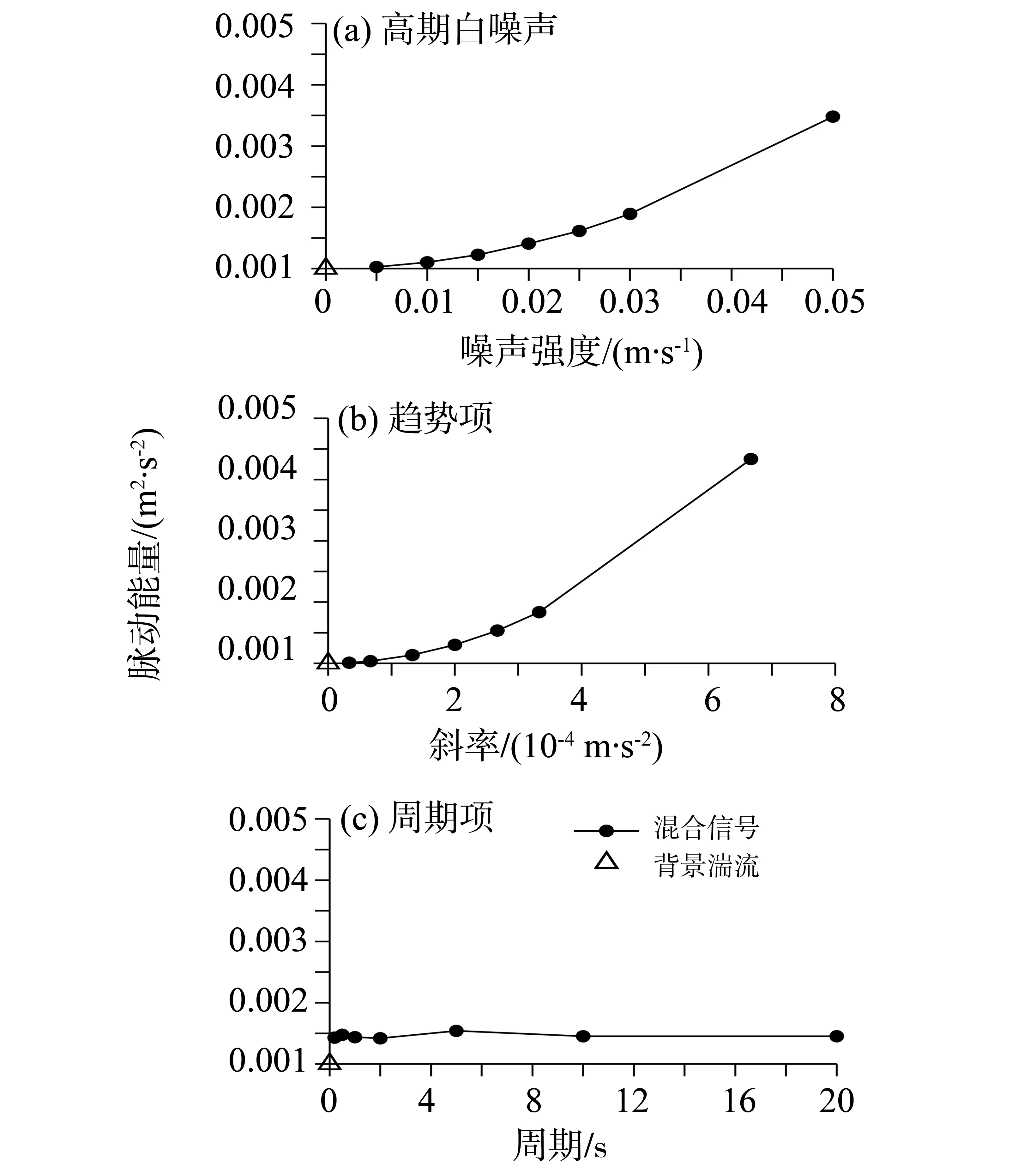
图7 脉动能量随噪声特征参数的变化Fig.7 Variation of turbulent energy with noise characteristic parameters

对于湍动能耗散率的估算，采样“惯性耗散法”[19]。应用该方法，需要根据各组数据的能谱来确定各自的惯性子区带宽。从背景湍流的能谱图中，确定其惯性子区约在0.5～10 Hz之间(图2c)。图8显示的是3种不同类型的噪声对能耗率的影响。可以看出，① 对于高斯白噪声，随着噪声强度的增大，能耗率有增大的趋势，但当噪声强度和湍流强度相当时，此时能谱惯性子区已被噪声污染，不适宜再用“惯性耗散法”进行能耗率的估算。② 对于趋势项，能耗率的估算几乎不受影响，这与上文分析趋势项对能谱的影响结果一致。③ 对于周期项，可以发现当周期项噪声的特征频率落在惯性子区时，对能耗率的估算有很大的影响，计算的能耗率比背景湍流的能耗率大1个量级。随着周期项的特征频率远离惯性子区，周期项噪声对能耗率的影响逐渐减小。当周期项大于5 s时，对于能耗率的估算几乎没有影响。由于波浪的周期约为100s，因此在受波浪影响显著的浅水区域，对能耗率的估算需考虑把波浪的信息滤掉。

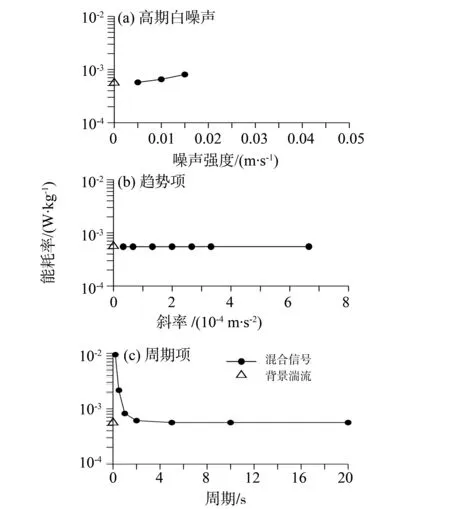
图8 能耗率随噪声特征参数的变化Fig.8 Variation of turbulent energy dissipation rate with noise characteristic parameters

4 结 论

基于河口底边界层实测湍流资料，选取了高斯白噪声、线性趋势项和周期项这3种不同类型的噪声，讨论了各种噪声对湍流信号的影响。

1)当湍流信号混入3种类型的噪声后，其概率分布仍能较好地满足准正态分布，因此通过概率分布判断测量数据是否包含湍流信号的做法不可取，而通过考察能谱曲线是否满足-5/3律是判断测量数据中湍流信息是否明显的较有效方法。

2)白噪声对能谱曲线有较大影响，当白噪声强度和湍流强度相当时，可显著改变能谱的分布规律。趋势项对能谱曲线的影响不大，而周期项仅对其特定频率的能谱值有影响。

3)在湍强、脉动能量和湍动能耗散率3个湍流特征参数中，白噪声对3种参数均有影响，当白噪声强度与湍流强度相当时，湍强和脉动动能分别增大37%和89%。趋势项仅对湍强和脉动能量有影响，其增幅值与白噪声所产生的效应相当。周期项使湍强和脉动能量产生的增幅分别为20%和40%，当周期项的频率落在惯性子区的频带时，能耗率会增大一个量级。

4)各种类型的噪声对湍流信号会造成不同程度的影响，如何从原始的测量数据中有效地把湍流信号和噪声分离，是下一步值得探讨的问题。

[1] HINZE J O. Turbulence[M]. 2nd ed. New York: McGraw-Hill, 1975.

[2] FUGATE D C, FRIEDRICHS C T. Determining concentration and fall velocity of estuarine particle populations using ADV, OBS and LISST [J]. Continental Shelf Research, 2002, 22: 1867-1886.

[3] VOULGARIS G, MEYERS S T. Temporal variability of hydrodynamics, sediment concentration and sediment settling in a tidal creek [J]. Continental Shelf Research, 2004, 24: 1659-1683.

[4] GORING D G, NIKORA V I. Despiking acoustic doppler velocimeter data [J]. Journal of Hydraulic Engineering, 2002, 128(1): 117-126.

[5] MORIN, SIZUKI T, KABUNO S. Noise of acoustic doppler velocimeter data in bubbly flows [J]. Journal of Engineering Mechanics, 2007, 133: 122-125.

[6] TROWBRIDGE J H, ELGAR S. Turbulence measurements in the surf zone [J]. Journal of Physical Oceanography, 2001, 31: 2403-2417.

[7] WAHL T L. Discussion of despiking acoustic doppler velocimeter data [J]. Journal of Hydraulic Engineering, 2003, 129(6): 484-487.

[8] PARSHEN M, SOTIROPOULOS F, PORTE-AGEL F. Estimation of power spectra of acoustic-doppler velocimetry data contaminated with intermittent spikes [J]. Journal of Hydraulic Engineering, 2010, 136(6): 368-378.

[9] CHANSON H, TREVETHEN M, AOKI S. Acoustic doppler velocimetry(ADV) in small estuary: field experience and signal post-processing [J]. Flow Measurement and Instrumentation, 2008, 19: 307-313.

[10] 鲁远征, 吴加学, 刘欢. 河口底边界层湍流观测后处理技术方法分析[J]. 海洋学报, 2012, 34(5): 39-49

[11] 刘欢, 吴超羽. 河口湍流数据现场采集和后处理[J]. 海洋工程, 2011, 29(2): 122-134.

[12] 刘欢, 吴超羽, 许炜铭. 珠江河口底边界层湍流积分尺度研究[J]. 海洋工程, 2008, 26(4): 125-131.

[13] LIU H, WU C Y, XU W M, et al. Contrasts between estuarine and river systems in near-bed turbulent flows in the Zhujiang (Pearl River) Estuary, China [J]. Estuarine, Coastal and Shelf Science, 2009, 83: 591-601.

[14] 刘欢, 吴加学, 武亚菊. 珠江河口底边界层憩流动力特征[J]. 海洋工程, 2013, 31(4): 55-61.

[15] 刘志宇, 魏皓. 黄海潮流底边界层内湍动能耗散率与底应力的估计[J]. 自然科学进展, 2007, 17(3): 362-369.

[16] 刘欢, 吴超羽, 许炜铭, 等. 珠江河口底边界层湍流特征量研究[J]. 海洋工程, 2009, 27(1): 62-69.

[17] EGBERT G D, RAY R D. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data [J]. Nature, 2000, 405(15): 775-778.

[18] WU J X, LIU H, REN J, et al. Cyclonic spirals in tidally accelerating bottom boundary layers in the Zhujiang (Pearl River) Estuary [J]. Journal of Physical Oceanography, 2011, 41(6): 1209-1226.

[19] SMITH W A M, KATZ J, OSBORN T R. On the structure of turbulence in the bottom boundary layer of the coastal ocean [J]. Journal of Physical Oceanography, 2005, 35(1): 72-93.