基于合作博弈的东江流域用水不确定性研究*

何艳虎，陈晓宏，林凯荣

(中山大学水资源与环境研究中心∥华南地区水循环和水安全广东普通高校重点实验室，广东 广州 510275)

1 研究背景

变化环境下，区域各部门用水量受人口和经济增长、下垫面变化、产业结构调整、节水和水价水市场等影响，表现出较大的不确定性，必然对地区需水预测及水资源优化配置产生重要影响。水资源优化配置是解决区域水资源短缺，实现各产业协调发展，保护生态环境和水安全保障的必要技术支撑之一，因此，区域用水的不确定性研究具有重要的理论和现实意义。目前，对部门用水的研究主要体现在不同空间尺度(流域、区域和城市)各产业的用水特点及用水量的变化特征分析[1-7]，用水结构的演变和驱动力分析及需(用)水量预测等方面[8]，其中需(用)水量预测研究主要集中于基于历史用水过程外延预测未来需(用)水、建立用水量预测模型，或者定额法、系统动力学模型及考虑定性因素的云模型等一些理论和方法的应用[9-11]。然而受气候变化和剧烈人类活动的影响，当前地区来水过程分布更趋不均，用水强度不断增加，各部门用水的不确定性增强，即影响部门用水量的因素在增多，传统方法试图从历史用水过程或建立考虑主要驱动因素的用水量变化模型方面分析用水的不确定性面临较大挑战，尤其是在当前用水总量控制的社会命题下，从用水系统角度，以各用水部门合作用水后的收益分配为出发点，进行变化环境下部门用水不确定性的研究目前还十分少见。冯·诺依曼等[12]提出的基于竞争联盟而做出决策的合作博弈理论可为解决这一问题提供一种新的途径。 因此，本文在阐述合作博弈理论的基础上，基于各用水户参与用水联盟的机会收益，建立和求解用水总量控制下基于合作博弈的各用水户用水分解模型，进行区域各部门用水的不确定性分析。并以广东省东江流域及其各分区部门的未来用水为例进行研究，通过各用水户用水量控制指标集的确定，为流域用水总量控制下未来的用水管理提供重要参考。

2 合作博弈

2.1 博弈论概况

博弈论(game theory)，又称对策论，即竞争环境下的多人决策理论，它研究在竞争环境中如何进行决策。关于博弈论最早的研究见于古诺(Cournot，1897)和埃奇沃斯(Edgeworth，1981)等对垄断和生产的论文，1944年，冯·诺依曼(J·Von Neumann)和奥斯卡·摩根斯坦(Oskar Morgensten)在具有里程碑意义的标志著作《博弈论与经济行为》(Game Theory and Economic Behaviour)中提出了博弈论的两个经典框架[12]：非合作博弈和合作博弈。基于此，半个多世纪以来，博弈论逐渐成熟，并广泛结合经济学研究应用于经济、政治、社会和军事等领域之中[13-17]。

2.2 合作博弈[12]

合作博弈假定参与人有一个可实施的共同行动的协议，即合作是外生的。它强调的重点在于：这些参与人会组成什么样的联盟？在联盟中，如何确定参与人之间的权势大小？如何合理地去分配联盟所得的合作收益(或分摊成本)？

2.2.1 联盟 对有n个局中人，即N= {1,2,…,n}，参与的博弈，称集合N的任何一个子集S为一个联盟。特殊情况，允许取S=φ和S=N。

2.2.2 特征函数 设博弈的局中人集合为N={1,2,…,n}，v(S)是定义在N的一切子集(即联盟)上的实值函数，其满足：

v(φ)=0

(1)

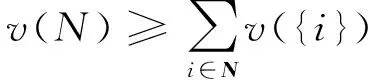
(2)

称v(S)为一个特征函数或联盟函数，它表示联盟S加入大联盟进行博弈的机会收益，或联盟S独立活动可获得的最大收益，这是进行合作博弈首先应确立的。给定局中人集合N和特征函数v(S)，所进行的合作博弈记为G=[N,v]。合作博弈的求解方法可归为“占优”和“估值”两大类。考虑到用水系统的特性，本文选用“占优”方法对用水分解模型进行求解。

2.2.3 转归 在n人合作博弈G=[N,v]中，设x=(x1,x2,…,xn)是一个n维向量，满足下面两个条件：

xi≥v({i})，i=1，2，…，n

(3)

(4)

则称x为一个转归(imputation)，或称分配，全体转归称为转归集，记为I(N,v)。

2.2.4 核心 设G=[N,v]是一个n人合作博弈，若存在一个转归x=(x1,x2,…,xn)∈I(N,v)，使得对所有S⊆N，满足

(5)

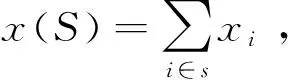
C(v)={x|x∈I(N,v),v(S)≤x(S),S⊂N}

(6)

若ε是一个实数，非空的预转归子集称为G的强ε-核心，记为C∈(v)：

(7)

ε起到对核心调节的作用，即ε>0时，可以使合作博弈的原核心由空集变为非空的强ε-核心，而当ε<0时,则加强了对x的要求，可以使合作博弈的核心集合变小。

若ε0是使得强ε-核心Cε0(v)≠φ的最小ε，则称Cε0(v)为G的最小核心，记为LC。

3 基于合作博弈的区域用水不确定性研究

3.1 研究区概况

东江流域位于珠江三角洲的东北端，地区范围在22°38′～25°14′N，113°52′～115°52′E[18]。东江是河源、惠州、东莞、广州、深圳以及香港3 000余万人口的生产、生活、生态用水的水源地[18]。涉及的各市总人口约占广东省总人口的4成，GDP约占广东全省GDP总量的7成(约3万亿元)，具有举足轻重的政治、社会、经济地位。尤其是对港供水的特殊性，使得东江供水安全具有重大的政治经济意义。流域多年平均径流量为326.6亿m3，目前，东江流域河道外年取水总量已经超过90亿m3，总量上已十分接近东江流域90%来水频率下的年分水总量(106.64亿m3)，供用水强度大，现状用水量已接近饱和。受气候变化影响，加之博罗以下河段的过量采砂，流域下游受咸潮影响大，对流域供水安全构成威胁。

3.2 数据

本次研究范围为广东省东江流域河源、惠州、东莞、广州、深圳及新丰、兴宁等市县，所用数据为近30年来人口、GDP和各产业用水量等主要社会经济、水资源及其开发利用指标序列。该时间序列源于《广东省水资源公报》及各地市统计年鉴。

3.3 基于合作博弈的东江流域用水不确定性研究

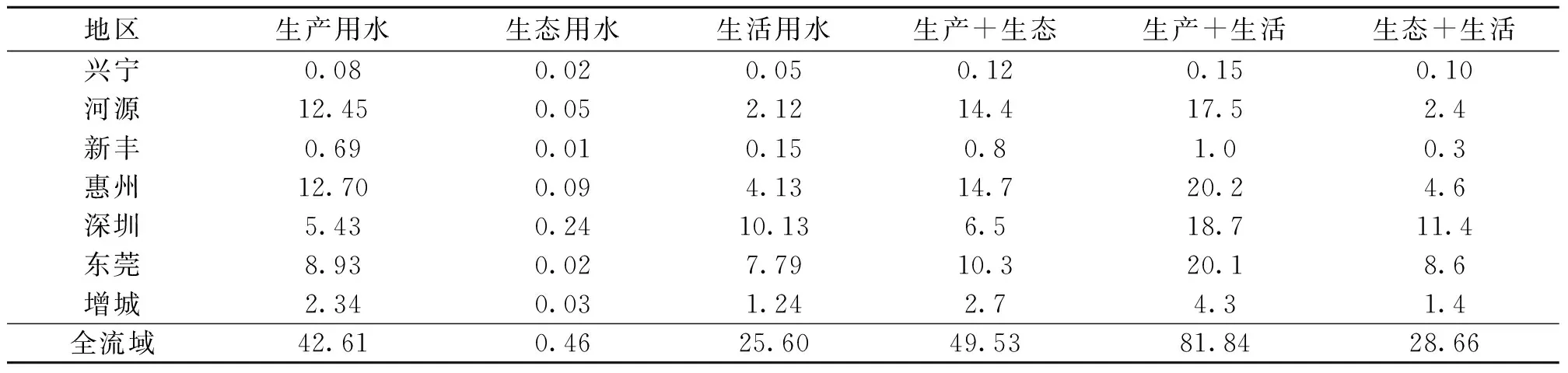
按照《全国水资源综合规划技术大纲》中用水统计的新口径规定[19]：区域用水一般分为生产用水、生态用水和生活用水3大类。依据合作博弈理论，区域生产用水、生态用水和生活用水可组成一个用水大联盟，各用水户有一个可实施的共同行动的协议，即用水总量控制指标。要解决的问题有：各用水户(3个局中人)可能组成哪些用水联盟(S)？如何确定各用水户在用水联盟中权势的大小？如何将合作后的联盟收益(用水总量控制指标)在各用水户间进行合理分配？进行基于合作博弈的用水不确定性研究首先应确立联盟S加入用水大联盟N进行博弈的机会收益v(s)，这是构成用水大联盟及对其所得收益进行合理分配的基础[12]。目前对国民经济各行业用水特性的分析[5]、用水效益评估指标和方法的选择等研究较多[20-22]，但对各用水户之间用水机会收益的研究尚少。鉴于本文重点不在于探讨用水机会收益，参考用水效益确定方法，考虑各用水户近30年来用水量变化特征，依据现状用水和地区发展目标，确定其参与用水大联盟所获得的机会收益v(i) ，具体表现为可分配的用水量，以体现用水的合作博弈性质。用水联盟S的机会收益v(s)则为参与结盟的各用水户考虑用水量平均增长率之后的机会收益v(i)之和。各分区用水户用水机会收益之和即为流域各用水户及其联盟用水机会收益(表1)。用水大联盟N的收益v(N)参考2020年广东省用水总量控制指标分解方案确定(表2)，因此，这里各用水户用水机会收益体现为相应用水部门获得的用水量的大小。据此，可以建立用水总量控制下的东江流域及其各分区基于合作博弈的各用水户用水分解模型并对其求解，以分析该地区未来用水的不确定性。

表1 东江流域2020年各分区用水户参与用水联盟机会收益
Table 1 The opportunity incomes of water alliance for each water use sector of each sub-region in the Dongjiang river basin in 2020

108m3

表2 东江流域2020年各分区用水总量控制指标
Table 2 The total water use control indicator for each sub-region in the Dongjiang river basin in 2020

108m3

不失一般性，以深圳市为例，对其各用水户用水分解模型采用占优方法进行合作博弈求解。

生产用水、生态用水和生活用水分别用1, 2, 3表示，对于生产用水、生态用水和生活用水组成的合作博弈G=[N,v]，其中N={1, 2,3 }，由表1可知，其特征函数为：

v(φ)=0，v({1})=5.4，v({2})=0.24，

v({3})=10.13 ，v({1,2})=6.5，

v({1,3})=18.7，

v({2,3 })=11.4，v({1, 2,3})=21.06。

由核心C(v)的定义，转归x(x1,x2,x3)∈C(v)的充分必要条件为：

X1≥v({1})=5.4；

X2≥v({2})=0.24；

X3≥v({3})=10.13；

X1+X2≥v({1,2})=6.5；

X1+X3≥v({1,3})=18.7；

X2+X3≥v({2,3})=11.4；

X1+X2+X3=v({1,2,3})=21.06。

依上述不等式，可画出平面上的重心三角形△123(即高为v(N)的等边三角形)，以及各不等式要求，见图1(a)。可知，图1(a)中转归集I(N,v)为三角形△MNQ内的点集，而阴影六边形ABCDEF则为核心C(v)，其中4个顶点的坐标分别为A(9.66，1.27，10.13), B(9.66，0.24，11.16), C(6.26，0.24,14.56), D(5.4，1.1,14.56) , E(5.4，2.36,13.3) , F(8.57，2.36,10.13)。阴影六边形内的点集即为深圳市2020年用水总量控制下生产、生态和生活用水可获得的收益区间，或是可分得的水量取值范围。三大用水部门通过合作博弈，获得总量为21.06亿m3的用水收益，在满足用水总量控制指标的要求的同时，也使得各部门通过协调合作，该地区总的用水效益实现最大化，以促进水资源的可持续利用。以此类推，东江流域其余各分区及全流域生产、生态和生活用水合作博弈的核心见图1(b)～(h)。图三大用水部门用水合作博弈核心在考虑各用水户用水机会收益的基础上，实现了未来用水的不确定性合理预测和分析，更符合实际生产实践情况，同时也解决了传统的需(用)水预测只是给出需(用)水量一个确定的数值，无法确定预测结果可能的波动范围的问题。

三大用水部门的用水合作博弈核心为未来水平年的区域用水控制指标管理提供了参考，具体表现在核心内的点集，每个点的三维数值分别代表了生产、生态和生活用水的控制水量。但在实际生产实践过程中，由于各部门用水受有效供水量、用水效率和管理水平等诸多因素影响，相应的用水机会收益可能会表现出一定的随机性，而用水联盟参与大联盟的机会收益是进行合作博弈分析的基础，因此，用水机会收益的随机性可能会使得用水合作博弈的核心为空集或包含无穷多点集。为进行用水不确定性的合理分析，可以使用强ε-核心，即Cε(v)，来对核心进行调节，以达到分析目的。ε可取任何实数，由式(7)可知，ε可以有一个最小值，使得合作博弈的核心不为空，ε的值可依研究目的，可随核心集的大小而定，具体表现为联盟机会收益的一部分，在用水合作博弈中可以视为生产、生态和生活用水部门能获得的用水总量的一部分。

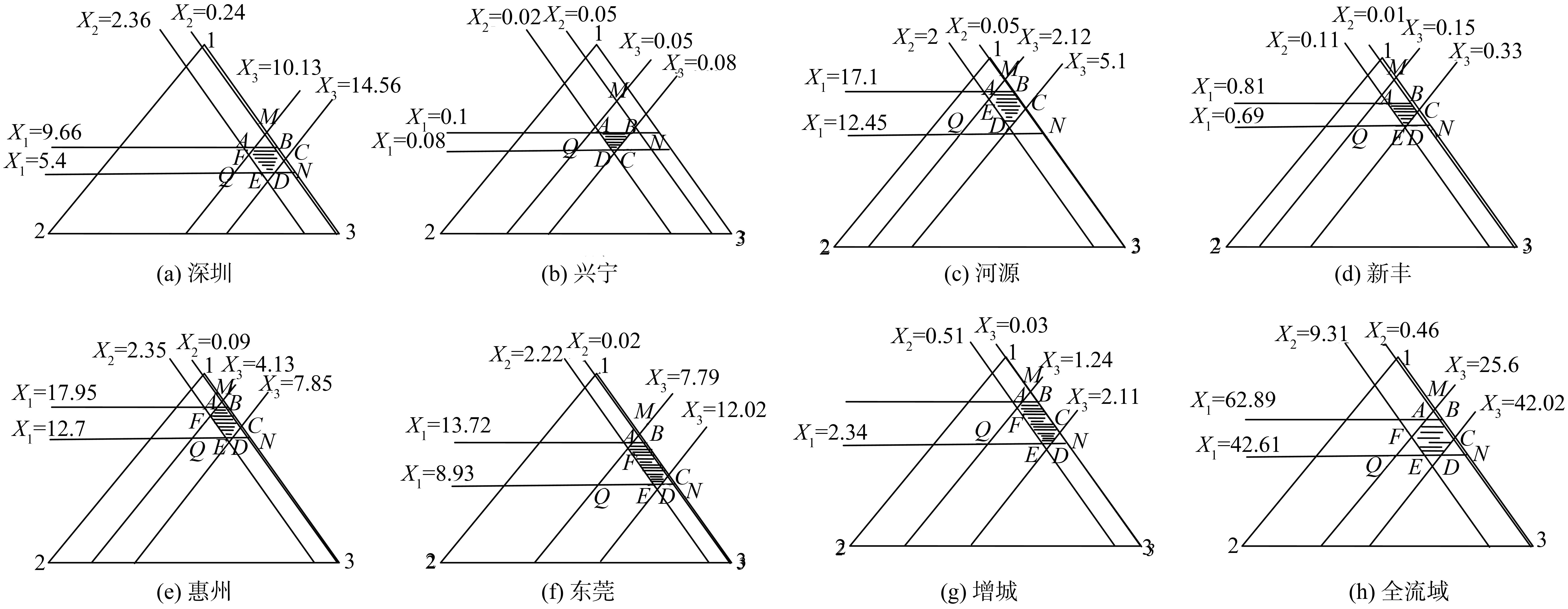
图1 东江流域及各分区2020年生产、生态和生活用水合作博弈核心(108m3)Fig.1 The cooperative game theory cores of productive, domestic and ecological water supply of the whole Dongjiang river basin and its sub regions in 2020

现以全流域用水合作博弈核心图1(h)为例，进行说明：

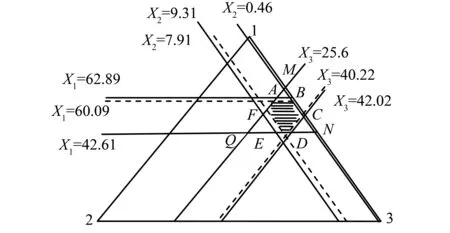
图2 东江流域2020年生产、生态和生活用水合作博弈核心及ε-核心(ε=0.9)(108m3)Fig.2 The cooperative game theory cores of productive, domesticand ecological water supply of the whole Dongjiang river basin in 2020 and its ε core(ε=0.9)

从图1(h)可以看出，东江流域用水合作博弈核心不为空，为加强对核心的要求，可以使ε取负值，使用水合作博弈的核心变小，以使目标值出现在合理的区间范围内。参考东江流域近10年来的用水平均变化幅度(±1.3%)，以ε取v(N)的-1%为例，由强ε-核心的定义和式(7)，x=(x1,x2,x3)∈C1(N,v)应满足以下条件要求：

x1+x2-2×0.9≥49.53；x1+x3-2×0.9≥81.84；x2+x3-2×0.9≥28.66

在图1(h)的重心三角形△123中，可得C1(N,v)为核心六边形ABCDEF内虚线所围的阴影部分(图2)。可以看出，在经过ε调节后，对用水合作博弈的核心要求有所提高，如对生产、生态和生活用水的控制量分别由62.89亿m3，9.31亿m3和42.02亿m3分别压减至60.09亿m3，7.91亿m3和40.22亿m3，这种用水合作博弈核心点集的减少或核心的突出将使得用水的不确定分析更具针对性，更能体现变化环境下经济社会发展对水资源的需求，从而更好地应用于用水管理中。

以上基于合作博弈的各用水户用水分解模型分析表明，合作博弈理论用于部门用水的不确定性分析一方面可解决传统需(用)水预测时未能很好地考虑部门用水的机会收益问题，如各用水户相互协调用水可获得的综合效益，另一方面也避开了对需(用)水驱动和胁迫因素的选择及各因素对用水的作用量化，能给出满足用水总量控制指标和一定用水效益的各用水户用水量取值区间，更符合变化环境的实际和应用于实践，这为变化环境下基于用水总量控制的区域用水不确定性分析提供了一种新的途径和量化手段。

4 结 论

本文利用基于合作博弈的各用水户用水分解模型，在考虑各用水户参与用水联盟所获得机会收益的前提下，求解用水合作博弈的核心及强ε-核心，并以典型研究区东江流域为例，分析各用水户未来用水的不确定性，这为研究基于用水总量控制的部门用水不确定性提供了一种新的方法和途径。主要研究结论如下：

1)通过对合作博弈的转归集及核心推求，给出了2020年广东省东江流域及其各分区生产、生态和生活用水合作博弈的核心，即各用水部门用水控制量可能的取值范围，东江流域2020年生产、生活和生态用水控制量区间分别为42.61～62.89亿m3，25.2～42.06亿m3和0.46～9.31亿m3；

2)通过对研究区2020年用水合作博弈强核心的推求，生产、生态和生活用水的控制量分别由62.89亿m3，9.31亿m3和42.02亿m3分别压减至60.09亿m3，7.91亿m3和40.22亿m3；

3)研究区各用水户用水量控制指标在保障未来流域经济社会持续发展对水资源需求的同时，与国家分配给流域总的用水量控制指标也进行了很好衔接，这将为东江流域水资源可持续利用和未来用水管理提供重要参考。

合作博弈理论与方法已在经济管理、政策制定和税收治安等领域广泛得到应用，而在水资源评价与管理等方面的研究却十分少见，因此，如何将合作博弈的优势与变化环境下水资源管理的特点广泛地结合，如在用水合作博弈中，如何更合理地确定用水联盟的机会收益和核心调节值ε等，尚需在今后做进一步研究。

[1] 郭磊, 黄本胜, 邱静, 等 . 核电站淡水用水特征综合分析研究 [J]. 水利学报, 2013, 44(5) : 615-621.

[2] 程孟孟, 陈进 . 南北方典型省份产水和用水特点比较 [J]. 长江科学院院报, 2012, 29(11) :1-4, 15.

[3] 杨有德, 张有芷 . 长江流域用水状况分析 [J]. 人民长江, 2006, 37(8) :10-11, 17.

[4] 张士锋, 贾绍凤 . 黄河流域近期用水特点与趋势分析 [J]. 资源科学, 2002, 24(2) : 1-5.

[5] 汪党献, 王浩, 倪红珍, 等. 国民经济行业用水特性分析与评价 [J]. 水利学报, 2005, 36(2) :167-173.

[6] LUIS SP, IAN C, IACOVOS I. Improved indicators of water use performance and productivity for sustainable water conservation and saving. Agricultural Water Management,2012,108:39-51.

[7] NEAL J S, FULKERSONB W J, HACKER R B. Differences in water use efciency among annual forages used by the dairy industry under optimum and decit irrigation [J]. Agricultural Water Management,2011,98:759-774.

[8] 许士国, 吕素冰, 刘建卫, 等. 白城地区用水结构演变与用水效益分析 [J]. 水电能源科学, 2010, 30(4):106-108, 214.

[9] 张薇, 邹志红, 王惠文 . 城市日用水量预测模型及其应用 [J]. 系统工程, 2010, 28(3) : 93-97.

[10] AlIREZA G, SAEID E, ALI M, et al. Water transfer as a solution to water shortage: Ax that can Backre [J]. Journal of Hydrology,2013,49:23-39.

[11] 袁宝招, 陆桂华, 李原园, 等. 水资源需求驱动因素分析 [J]. 水科学进展, 2007, 18(3) :405-409.

[12] 汪贤裕,肖玉明. 博弈论及其应用[M].北京: 科学出版社,2008.

[13] SALAZAR R, SZIDORSZKY F, COPPLOA E, et al.Application of game theory for a groundwater conict in Mexico [J]. Journal of Environmental Management,2007,84:560- 571.

[14] KAVEH M. Game theory and water resources[J]. Journal of Hydrology,2010,381:225-238.

[15] 沈坤荣, 付文林. 税收竞争、地区博弈及其增长绩效 [J]. 经济研究, 2006(6) :16-26.

[16] 陆杉. 农产品供应链成员信任机制的建立与完善——基于博弈理论的分析 [J]. 管理世界, 2012(7) :172-173.

[17] 卢周来. 合作博弈框架下企业内部权力的分配 [J]. 经济研究, 2009(12) :106-118.

[18] 陈晓宏,刘德地,刘丙军,等. 湿润区变化环境下的水资源优化配置-理论方法与东江流域应用实践[M].北京:中国水利水电出版社,2011.

[19] 蔡国英, 徐中民. 黑河流域中游地区国民经济用水投入产出分析-以张掖市为例 [J]. 冰川冻土, 2013, 35(3):770-775.

[20] 秦长海, 赵勇. 不同节水措施下宁夏水资源利用的经济效益分析 [J]. 资源科学, 2008, 30(8) :1135-1140.

[21] 严婷婷, 贾绍凤. 关于国民经济用水投入产出分析指标的讨论 [J]. 水利经济, 2009, 27(6) :24-28.