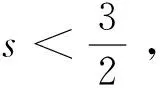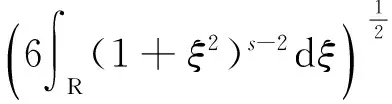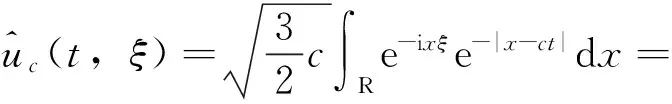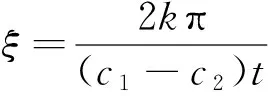修正Camassa-Holm方程的Cauchy问题*
张双虎,冯兆永,杨凯波
(1.西南大学数学与统计学院, 重庆 400715;2.中山大学数学与计算科学学院, 广东 广州 510275)
在本文,我们考虑如下直线上修正Camassa-Holm方程(mCH方程)的初值问题
(1)
这里
(2)
表示系统的动量密度。这个非线性方程通过对修正 Korteweg-de Vries方程的bi-Hamiltonian 表示应用 tri-Hamiltonian 对偶方法而导出[1-2],因此它是具有 bi-Hamiltonian 结构的可积系统。方程(1)描述平直底面上浅水表面波的无向性传播,u(t,x)表示非维数变量的自由表面高度。
Camassa-Holm 方程(CH 方程)
mt+umx+2mux=0,m=u-uxx
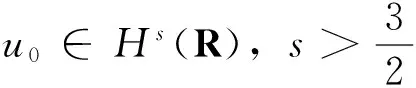
CH 方程具有二次非线性项,最近有两个具有三次非线性项的CH型方程被导出:mCH方程(1)和Novikov方程[16]
mt+u2mx+3muux=0,m=u-uxx
(3)
这两个方程都具有尖峰孤立子解并且都能描述波的破裂。最近,mCH方程(1)的几何形成和可积性、局部适定性、爆破准则和破裂机制、尖峰解以及尖峰孤立子的稳定性获得了研究[17-19]。
本文的目标是对(1)的 Cauchy 问题,提出奇异性形成的一些充分条件,建立解不连续依赖于初值意义下的不适定性。首先将mCH方程(1)改写成关于动量密度(2)的运输方程
(4)
运输方程的理论保证了解m保持正常和不爆破,只要斜率
(5)
保持有界;而当斜率(5)下方无界时,解在有限时间爆破[17-18]。当初值保号时,动量密度满足运输方程还隐含了动量m(t,x)和强解u(t,x)保持相同的符号,这对本文爆破结果的提出至关重要。我们提出的新的爆破利用了下述守恒律
以及作者最近建立的更好的估计(见引理4)。受文献[10]启发,我们利用文献[18]中给出的(1)的尖峰孤立子建立了非一致依赖性。这一结果的建立,使得我们对初值所在空间的指标有了一个较为清晰的刻画。
记号在下文中,对给定的 Banach 空间X, 其范数记为‖·‖X。 在不引起混淆的情况下,我们总是省略函数空间的定义域。函数u的Fourier 变换记为u或
1 基本引理
我们回顾修正 Camassa-Holm 方程的基本结果,读者可以通过文献[17-18]查阅细节和证明。首先我们给出局部适定性。
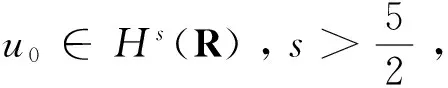
利用上述准则,我们可得以下爆破准则。
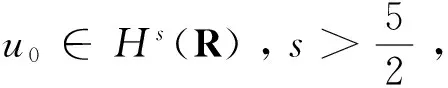
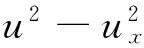
(6)
我们可得以下引理。
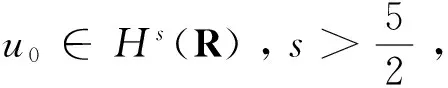
(t,x)∈[0,T)×R
进一步,
m(t,q(t,x))qx(t,x)=m0(x),(t,x)∈[0,T)×R
2 爆破现象
我们讨论 mCH 方程初值问题的爆破现象。首先引出一个重要引理,通过这个引理我们可以改进其已经确立的爆破结果。
引理4[20]设u0∈Hs(R),s≥2以及T>0是初值问题 (1) 对应的解u(t,x)的最大存在时间,则
(7)
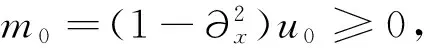
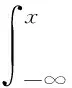
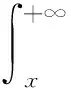
进一步
|ux(t,x)|≤u(t,x)
现在我们陈述本文第一个重要的定理。
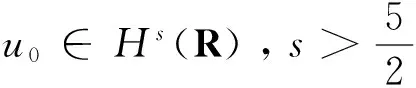
(8)
则解u(t,x)在有限时刻T0爆破
(9)

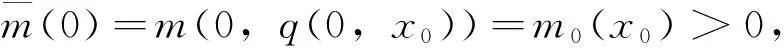
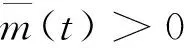
(10)
方程(1)和方程(6)可推出对t∈[0,T),
(11)
并且,结合引理5,(7)式以及(10)式, 易得
(12)
利用(11)-(12)式,通过简单计算可知成立
(13)
以下我们声明对所有t∈[0,T), 总有
(14)
事实上, 如果(14)式不成立,则由初始条件(8)可知,必存在时间t0∈(0,T)使得
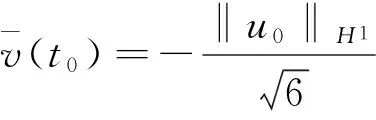
(15)
从而
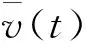
这与(15)式相矛盾。
结合(11)式、(13)-(14)式,对所有t∈[0,T),有
(16)
上式从0到t积分可得
从而,可推知存在0 进一步,由于 从而 当t→T≤T0 (17) 这就证明了解u(t,x)在有限时间T爆破。 注1 定理1不仅在初始条件上提升了文[18]中定理5.2,并且爆破时间的估计更优 注意到 mCH 方程(1)具有性质:若u(t,x)是(1)的解, 则v(t,x)=-u(t,x)也是(1)的解。因而,通过类似于定理1的分析,可以建立如下m0非正时的爆破结果。 (18) 则解u(t,x)在有限时刻T0爆破 (19) 引理6[18]对任何a≠0, 具尖峰形式的函数 是(1)的一个整体弱解。 为了证明上述定理,我们首先提出一个关键引理。 (20) 以及 (21) 其中 证明由引理6, 对任何c>0 考察 首先,通过计算uc关于x的Fourier变换可知 (22) 因此,当t=0时可得 (23) 另一方面, 当t>0 时, (24) 其中 则可以推出 (25) 结合(24)-(25)式可知 C2(s)2n1+4|s|+2st3-2s 进一步,得 最后,很容易知道定理2是引理7的一个直接结果。 注2 分析文献[17-18]中的定理和本文中的定理2, 我们知道在局部适定性和非适定性之间的指标存在间隔,这是我们以后研究努力弥补的方向。 [1] FUCHSSTEINER B. Some tricks from the symmetry-toolbox for nonlinear equations: generalizations of the Camassa-Holm equation [J]. Physica D, 1996, 95: 229-243. [2] OLVER P, ROSENAU P. Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support [J]. Phys Rev E,1996, 53: 1900-1906. [3] CAMASSA R, HOLM D. An integrable shallow water equation with peaked solitons [J].Phys Rev Lett, 1993, 71: 1661-1664. [4] FUCHSSTEINER B, FOKAS A. Symplectic structures, their Bäcklund transformations and hereditary symmetries [J]. Physica D, 1981/1982, 4: 47-66. [5] DAI H. Model equations for nonlinear dispersive waves in a compressible Mooney-Rivlin rod [J]. Acta Mech, 1998, 127: 193-207. [6] CONSTANTIN A, ESCHER J. Global existence and blow-up for a shallow water equation [J]. Ann Sc Norm Super Pisa Cl Sci, 1998, 26(4): 303-328. [7] LI Y, OLVER P. Well-posedness and blow-up solutions for an integrable nonlinearly dispersive model wave equation [J]. J Differential Equations, 2000, 162: 27-63. [8] RODRIGUEZ-BLANCO G. On the Cauchy problem for the Camassa-Holm equation [J].Nonlinear Anal, 2001, 46: 30-327. [9] YIN Z. Well-posedness, blowup, and global existence for an integrable shallow water equation [J]. Discrete Contin Dyn Syst, 2004, 11: 393-411. [10] HIMONAS A, MISIOLEK G. The Cauchy problem for an integrable shallow water equation [J]. Differential Integral Equations, 2001, 14: 821-831. [11] CONSTANTIN A. Existence of permanent and breaking waves for a shallow water equation: a geometric approach [J]. Ann Inst Fourier (Grenoble), 2000, 50: 321-362. [12] CONSTANTIN A, ESCHER J. Well-posedness, global existence, and blowup phenomena for a periodic quasi-linear hyperbolic equation [J]. Comm Pure Appl Math, 1998, 51: 475-504. [13] CONSTANTIN A, ESCHER J. Wave breaking for nonlinear nonlocal shallow water equations [J]. Acta Math, 1998, 181: 229-243. [14] XIN Z, ZHANG P. On the weak solutions to a shallow water equation [J]. Comm Pure Appl Math, 2000, 53: 1411-1433. [15] XIN Z, ZHANG P. On the uniqueness and large time behavior of the weak solutions to a shallow water equation [J]. Comm Partial Differential Equations, 2000, 27: 1815-1844. [16] NOVIKOV V. Generalizations of the Camassa-Holm equation [J]. J Phys A, 2009, 42: 342002. [17] FU Y, GUI G, LIU Y, et al. On the Cauchy problem for the integrable modified Camassa-Holm equation with cubic nonlinearity [J]. J Differential Equations, 2014, 255: 1905-1938. [18] GUI G, LIU Y, OLVER P, et al. Wave-breaking and peakons for a modified Camassa-Holm equation [J]. Comm Math Phys, 2013, 319: 731-759. [19] LIU X, QIAO Z, YIN Z. On the Cauchy problem for a generalized Camassa-Holm equation with both quadratic and cubic nonlinearity [J]. Commun Pure Appl Anal, 2014, 13: 1283-1304. [20] LIU Y, OLVER P, QU C, et al. On the blow-up of solutions to the modified integrable Camassa-Holm equation [J]. Analysis and Appl,2014,12(4):355-368.
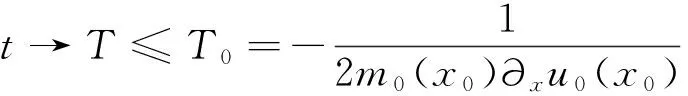
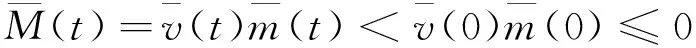
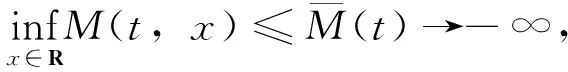
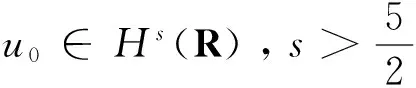
3 非一致连续依赖性