时深标定中VSP时深关系调整影响因素分析

姜本厚，张 凯,张平平,蔡越钎,王玉英

(1.中海石油(中国)天津分公司勘探开发研究院，天津塘沽 300452；2.中国石油大学(华东)地球科学与技术学院)

时深标定是联系时间域(地震)与深度域(地质、测井)关系的桥梁和纽带，也是合成记录制作中的核心问题，在地震资料精细解释和砂体标定中发挥着重要的作用[1-3]。随着勘探难度的加大，对时深标定精细程度的要求也越来越高，特别是随着VSP资料的出现和广泛应用，利用VSP资料进行标定也成为当前时深标定的主要方法。

目前VSP时深关系被认为是最准确的时深关系[5]，并被广泛应用于合成记录制作中。但多年来笔者在渤海油田多口井的时深标定中发现，要使地震剖面与合成记录具有较好的对应关系，经常需要对VSP时深关系进行“整体时移”和“局部拉伸”。“整体时移”现象在标定中时有发生，最大整体时移量有时可达二十多毫秒，由于对如此大的整体时移量找不到合理的解释，有些研究者往往舍弃合适的子波极性不用，而选择使整体时移量最小的反极性子波，这就容易造成对储层认识的偏差；“局部拉伸”现象在时深标定中也普遍存在，且局部拉伸量往往随深度增加而呈现增加的趋势，有时会达到近百毫秒，有的研究者由于不能接受这样的拉伸量而宁愿选择地震剖面与合成记录不对应的情况。有的研究者认为局部拉伸是合理的，但对于引起如此大的拉伸量原因缺乏必要的认识和研究。

1 时深调整原因分析

时深调整涉及VSP时深关系和偏移剖面两个方面，因此，要弄清时深调整的真正原因，需要对VSP时深关系和偏移剖面及其两者存在的时差进行详细分析。

1.1 偏移剖面及其存在时差

根据惠更斯原理与 Kirchhoff 积分偏移理论[6]，地下模型可看作由很多散射点组成，地面观测信号则是所有到达地表的散射能量的叠加。Kirchhoff 积分偏移理论都是假设从震源点到散射点再到接收点的路径为直线，在速度为v的常速介质中，设从震源S到散射点再回到接收点R的地震波的传播路径如图1所示。整个过程的旅行时满足如下双平方根方程：

(1)

其中S和R分别是炮点和检波点位置；x是散射点(SP)的空间位置；X是DMO后地震道的空间位置；y是炮检中心点空间位置；h是半偏移距；τ是双程垂直旅行时间或偏移时间；t0是DMO校正后反射的双程旅行时；t'0是Hale(1984)DMO后反射的双程旅行时。

常规叠前时间偏移就是按上述时距关系将散射能量偏移归位到散射点正下方τ时间。对每个散射点，将偏移孔径内所有输入道对应此点的散射能量叠加起来就得到了它的像。

理论情况下，经过叠前时间偏移的剖面应该归位到正确的位置。对于地下某一深度的分界面，其地震反射波在偏移剖面上出现的时间也是唯一的。但研究发现，同一采集资料在不同时间或不同处理后，经常存在时差。如果在研究目的层段，要使两个资料较好的对应，经常需要整体时移，有的时移量超过20 ms，有的甚至还要反转极性(图2)。而且，一般两次处理资料的时差并不是常数，而是随时间变化的变量，如图3所示。在图2的目的层段(1.7 s)新老资料对应较好的情况下，新老资料在浅、深层对应不好，明显可以看到，新资料在浅层偏浅，而在深层偏深。要使浅、深层也能较好的对应，如果以新资料为准，浅层0.5 s处的老资料大致需要向上局部拉伸6 ms，深层2.8 s处的老资料需要向下局部拉伸16 ms。两次处理资料存在时差是地震处理过程后表现出来的一种现象。由于处理较复杂，需要从叠前时间偏移理论入手，对具体原因进行分析研究。

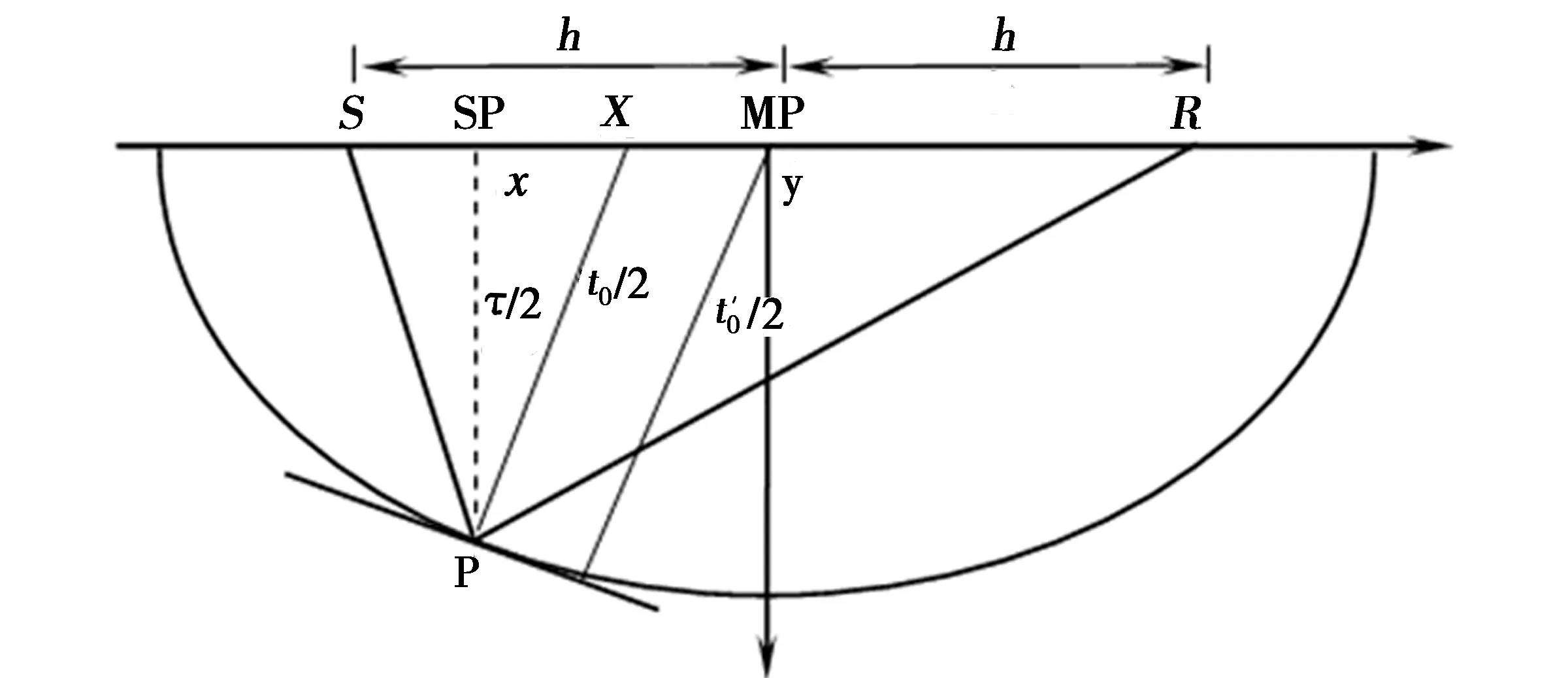
图1 叠前时间偏移的几何关系

图2 新资料上移10ms并颠倒极性

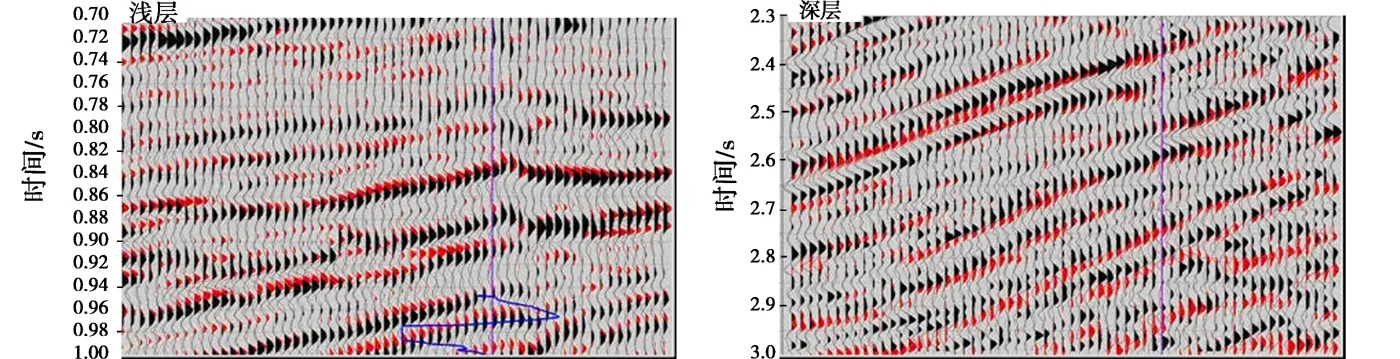
图3 新老资料在浅、深层的对比

1.1.1 纵向速度拾取不准引起时间偏移剖面时差

由叠前时间偏移脉冲响应椭圆方程和双平方根旅行时方程出发，根据图1中的几何关系可以得到DMO校正后反射的双程旅行时t0与双程旅行时t的关系式：

(2)

再由DMO校正后反射的双程旅行时t0可以解出双程偏移时间τ：

(3)

从方程(2)和(3)式不难发现，DMO校正后反射双程旅行时t0和双程偏移时间τ都与地层速度v呈正比关系，地层速度越大，t0和τ越大，地层速度越小，则t0和τ越小。

要获得准确的双程偏移时间τ，需要准确的地层速度v。因此速度分析时，拾取的速度准确程度和精度，直接影响到双程偏移时间τ的求取准确度和偏差。当拾取的速度比真实速度偏大时，双程偏移时间τ就会比真实时间偏大；当拾取的速度比真实速度偏小时，双程偏移时间τ值就会比真实时间小。在速度不准的情况下，偏差大小也随偏移距增大而增大。如表1所示，假设真实地层速度v为3 000 m/s，X为1 000 m，x为500 m，y为1 500 m，h为1 500 m，则真实双程偏移时间τ为2.808 s，当速度偏高10%时，计算的双程偏移时间τ比真实值偏大35 ms。当速度偏低10%时，计算的双程偏移时间τ比真实值偏小46 ms。

表1 速度变化对偏移时间影响统计

在实际地震处理的速度拾取中，由于浅层地震波能量较强，速度谱上能量团较集中，易于识别，因此浅层拾取的速度较准确，其求取的双程偏移时间也较准确，误差一般较小；随着深度增加，地震波能量逐渐衰减，多次波及干扰波的影响加大，速度谱上能量团一般较分散，速度的准确拾取变得困难，加上拾取的精度有限，使拾取的速度与真实速度的偏差也越来越大,误差也随之增大。

在渤海油田，东二下段、东三段广泛发育大套的低速泥岩，时深标定过程中经常发现，当井钻遇大套低速泥岩时，其拉伸量一般都较大。结合井曲线和速度谱曲线的分析认为，在速度拾取时，往往在低速泥岩段拾取的速度高于地层真实速度，因此，在进行NMO、DMO和偏移校正时，由于速度偏高，易造成校正量偏小，从而导致偏移时间过大，地震反射轴在时间剖面上偏深。其偏差大小主要是由拾取速度与真实速度的偏差引起的。

1.1.2 地震波相位变化引起的时差

地震波在地层中传播时，其波形和相位会受到大地滤波器的整形和改造作用，此外，实际资料处理过程中反褶积等与子波处理相关的处理手段也会引起相位变化，相位发生变化的地震波在时间域剖面反映同一深度界面时会存在时差。

1.1.3 各向异性引起的时差

常规处理方法是在地层各向同性的假设条件下进行的，但在实际的地下地层中，各向异性广泛存在，地震波不是沿直射线而是沿弯曲射线传播，地震波走时也不再是双曲线形式，随着偏移距与深度比的增大，各向异性引起的时差也会随之增大[7]。常规处理在不考虑各向异性的情况下，与地震波真实走时相比，计算的地震波走时不够准确，使反射层部分不在正确位置上，从而造成一定的时差。

1.1.4 偏移方法差异引起的时差

当地下情况比较复杂时，叠前时间偏移不再满足其假设条件，加上偏移速度拾取不准确，可能会造成偏移归位不准。此时，偏移剖面也会产生一定的误差。总之，纵向速度拾取不准、相位变化、各向异性、偏移方法差异等因素都会造成偏移剖面产生时差。而且这个时差是不容忽视的，甚至是时深调整量的主要原因。而纵向速度拾取不准是造成偏移剖面时差的主要影响因素。

1.2 VSP时深关系及时差

时间偏移剖面的检波器置于地表，沿地面布置观测点，“间接”测量地震波在垂直方向上的旅行时间和速度变化。与时间偏移剖面相比，VSP的检波器放在井中，在垂直方向上进行观测，“直接”测量地层垂直剖面上地震波的旅行时间和速度随深度的变化，且VSP的反射波旅行路径较地面地震反射波的旅行路径短；另外，由于地面观测受剖面浅部影响，地震波畸变较大，而VSP可观测到比较单纯的波形，因此，VSP确定的时深关系比时间偏移剖面可靠。

当地层为水平层状均匀介质时，对于直井零偏移距VSP而言，此时VSP时间传播路径跟VSP深度路径是一致的，故水平地层的VSP时深关系是可靠的。

当地层为倾斜层状均匀介质时，由于地震波传播遵循费马定理的最短走时原则，VSP时间不再沿深度路径传播，而是沿用时间最短的折线路径传播，此时得到的VSP时深关系就不准确，需要对倾斜地层引起的时差进行校正。

如图4所示，设倾斜地层的倾角分别为θi(i=1,2, ，……，n)，入射波与地层法向的夹角为αi，入射波到达每个倾斜界面的偏移距为xi，地层速度为vi，井点处的地层厚度为hi。则在井中海拔深度为Z处，VSP时间按照下式计算:

(4)

地震波沿深度路径传播的时间减去VSP时间就是因地层倾斜引起的VSP时差。在深度和厚度已知的情况下，VSP时差只是地层倾角的函数，它随地层倾角的增大而增大。张平平等(2011年)[8]用有限差分波动方程方法对多种倾斜角度的地层模型进行了正演模拟，研究结果表明，VSP时差随地层倾斜角度的增加而快速增大。当地层为砂泥岩互层时，VSP时差变化梯度小于阻抗递增模型。此外，在实际的VSP处理中，海上资料未作潮差校正、枪深及偏移距校正时的人为失误、VSP初至拾取不准及地层非均质性等因素也会引起一定的VSP时差，但这些时差跟地层倾斜引起的时差相比，一般都较小。

图4 倾斜地层VSP传播路径示意图

1.3 时深标定原则

时深标定是建立深度域地层界面与时间域地震反射轴间的对应关系。由于地震剖面不能局部拉伸和整体平移，而合成记录的调整比较方便，因此，时深标定是以实际偏移剖面为标准进行调整，即使在VSP时深关系比偏移剖面可靠的情况下。因此，时深调整中的“整体时移”主要是地震处理过程引起的，除地层倾斜以外的其它因素造成的VSP时差一般较小，对“整体时移”的贡献不大。而“局部拉伸”主要是由纵向速度拾取不准、相位变化引起的偏移剖面时差和由地层倾斜引起的VSP时差共同作用的结果，且纵向速度拾取不准是造成偏移剖面时差的主要因素。

2 应用实例

A井是渤海油田的一口探井，由于该井钻井深度大，虽然该井进行了VSP测井，但是，如图5所示，在深层用原始VSP时深关系标定的合成记录与叠前时间偏移剖面对应不上，需要进行较大调整才能达到较好的对应关系，其中该井基本不需要进行“整体平移”，而“局部拉伸”达到95 ms。从过A井地震剖面来看(图6)，该井已钻遇的地层存在倾斜层，因此需要明确因地层倾斜引起的VSP时差的大小。为了验证该井VSP时差大小，采用有限差分波动方程正演模拟方法，用该井的实测声波和密度曲线来近似模拟真实地层情况，正演模型采用水平地层形式，由于水平地层模型在VSP正演时，其深度路径和时间路径是一致的，将VSP正演的初至时间和VSP实测数据进行对比，即可确定每口井VSP时差的大小。该井VSP正演的初至时间和实测数据对比如图7所示，从图中来看， VSP正演的初至时间比VSP实测结果要大，且随地层倾角而变化，这跟VSP原理是符合的。对比结果表明，由于倾斜地层引起的VSP时差大致为35 ms。

图5 VSP调整前、后合成记录对比图

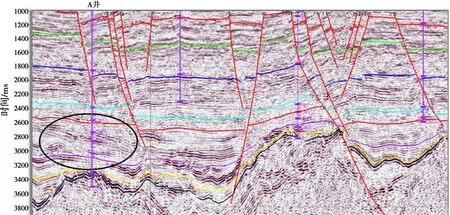
图6 过A井地震剖面

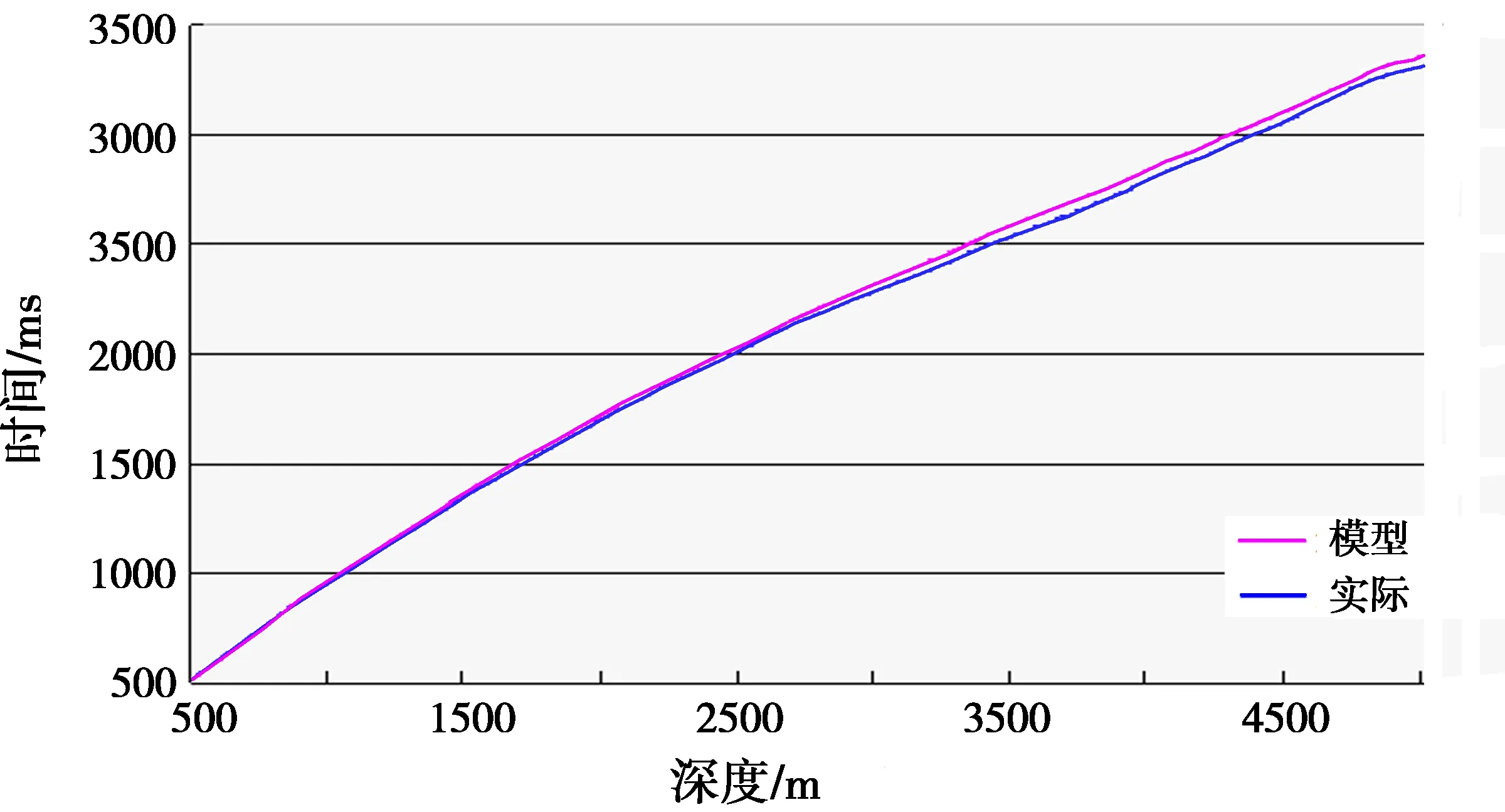
图7 A井VSP正演与实测结果对比

该井时深标定的局部拉伸量大致为95 ms，除去地层倾斜引起的35 ms的VSP时差，大致还有60 ms的时差，而这部分时差被认为是由偏移剖面时差引起的。原因在于该井在3 800～4 800 m处，存在约1 000 m的大套低速泥岩，而叠加速度转化为地震层速度后，明显高于低速泥岩的声波速度和VSP速度。结合上述(2)和(3)式可知，在地震速度比地层真实速度偏大的情况下，DMO校正后，反射双程旅行时和双程偏移时间的计算结果都会偏大，从而产生偏移剖面时差，偏差大小跟拾取的速度偏离真实速度的大小有关。

统计表明，在渤海油田，其它钻遇大套低速泥岩的井，其时深调整量也一般较大。且低速泥岩段拾取的速度一般较真实速度偏高，这也说明大套低速泥岩处的纵向速度拾取不准，是引起偏移剖面时差的主要因素。

通过上述典型实例分析认为，VSP时深关系的调整量是VSP和偏移剖面时差共同作用的结果。VSP时差主要是由于地层倾斜引起的。而偏移剖面时差主要是纵向速度拾取不准造成的。

3 结束语

(1)时深标定时，由于时深调整是以实际偏移剖面为标准，因此时深调整时经常需要“整体时移”和“局部拉伸”。调整量往往是VSP时差和偏移剖面时差共同作用的结果，且偏移剖面时差常是主要影响因素。

(2)通过叠前时间偏移理论分析，结合大量已钻井的时深标定结果，认为偏移剖面时差主要是纵向速度拾取不准造成的。

(3)与地面地震相比，VSP测量路径较短，且可以直接测量垂向的旅行时，所以VSP时深关系比偏移剖面更可靠。

(4)VSP时差主要是由于倾斜地层引起的，且VSP时差随倾角增大而增大。

(5)渤海油田东二下段、东三段广泛发育大套的低速泥岩，由于低速泥岩段的速度拾取偏高，在进行NMO、DMO和偏移校正时，易造成校正量偏小，从而导致偏移时间偏大，使地震反射轴在时间剖面上偏深。

[1] 孙学继,杨晓.合成地震记录制作方法研究[J].石油地球物理勘探，1997,32(增刊2):34-39.

[2] 杨海长,周玉.合成地震记录在层位标定中的几个关键问题[J].西南石油大学学报(自然科学版)，2009,31(4):52-57.

[3] 李国发,廖前进,王尚旭，等.合成地震记录层位标定若干问题的探讨[J].石油物探，2008,47(2):145-149.

[4] 陈广军.合成地震记录制作与标定中的争论及注意的问题[J].西安石油学院学报(自然科学版),2002,17(4):19-23.

[5] 曹统仁.VSP平均速度的应用[J].西南石油学院学报,1999,21(2):46-50.

[6] Schneider W A.Integral formulation for migration in two and threedimensions[J].Geophysics,1978,43(1)：49-76.

[7] 黄中玉,曲寿利,王于静,等.层状各向异性介质转换波克希霍夫叠前时间偏移[J].地球物理学报，2008, 52(12):3109-3115.

[8] 张平平,沈章洪,彭刚.VSP与地震偏移剖面时间的关系及其在勘探开发中的应用[M].北京：中国石化出版社，2011：119-123.