自适应小波阈值函数的指纹图像去噪

李 雷， 魏连鑫

（上海理工大学理学院，上海 200093）

指纹识别技术被广泛应用于公安刑侦和产品安全验证中，然而由于设备和环境等因素的影响，使得采集到的指纹图像质量比较差，给指纹的快速识别对比带来了一定的麻烦.传统的图像去噪［1］是在空间域实现的，主要方法有均值滤波法、中值滤波法和维纳滤波法.小波以其良好的时频特性和多分辨率特性，使其在去噪领域得到广泛的应用［2－10］.最早的小波阈值去噪方法是由Donoho提出的VisuShrink方法［7－9］，该方法在减少噪声的同时能保持图像的局部奇异性，但仍然会过度“扼杀”小波系数，造成一定程度的细节丢失.Chang［11］，Kaur［12］等改进了阈值的选取方法.本文针对指纹图像在采集过程中由于仪器或者传输通道而产生的高斯白噪声，改进了VisuShrink方法，提出了一种基于噪声强度和小波分解层数的自适应指纹去噪方法.

1 VisuShrink方法基本原理

原始图像和噪声在小波变换后有不同的统计特性，图像本身的能量对应着较大的小波系数，主要集中在低频部分，而噪声的能量对应着较小的小波系数，分布于整个小波域中.根据这一特性，可以找到一个合适的实数作为阈值，当小波系数的幅值大于该阈值时，予以保留；当小波系数的幅值小于该阈值时，将小波系数置零.

小波阈值图像去噪的主要步骤：a.选择合适的小波基函数和分解层数对噪声图像进行小波分解；b.在小波域对分解后的各层系数进行阈值处理；c.根据小波分解的低频系数和处理后的高频系数进行重构，得到去噪图像.

2 改进的阈值函数

2.1 改进的阈值函数

小波阈值去噪方法的关键是小波阈值的量化和阈值函数的选取.传统的阈值函数有软阈值和硬阈值，其函数表达式分别为

式中，sgn（wjk）表示wjk的符号；wjk为噪声图像的小波变换系数；w′jk为经过阈值函数处理后的小波系数；δ为阈值.

软阈值函数连续，处理结果相对平滑，但处理后的小波系数会发生一定的收缩，造成一定程度的边缘模糊等失真现象.硬阈值函数虽然可以很好地保留图像的边缘等局部特征，但由于其在阈值点处不连续，处理后的图像会出现震荡、伪吉布斯效应.另外，软、硬阈值函数都有过度“扼杀”小波系数的缺点，会使指纹图像中很多重要的细节信息丢失，对此，本文提出了一种改进的阈值函数

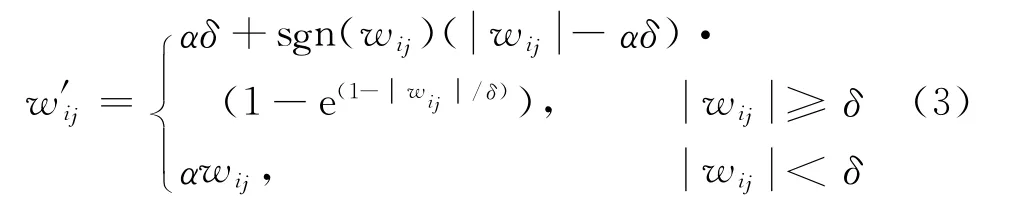
式中，α（0≤α≤1）为控制参数，其图像如图1所示.

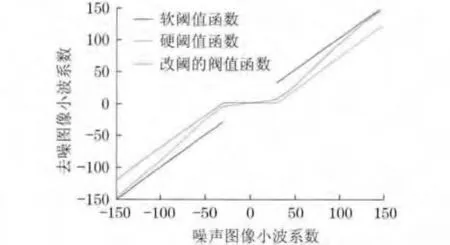
图1 3种阈值函数的对比（δ＝30，α＝0.2）Fig.1 Comparison of three kinds of threshold functions（δ＝30，α＝0.2）

2.2 风险性分析

Donoho等［7－9］利用极小化极大估计建立了软、硬阈值理论基础，并对这些阈值估计方法进行了详细讨论.假设噪声图像Y＝（yn）n∈［1，n］为原图像X＝（xn）n∈［1，n］的观测值，即Y＝X＋ζb.其中，ζ为噪声的方差，b＝（bn）n∈［1，n］为独立同分布的高斯白噪声.该观察模型经小波变换后在小波域中可表示为，wi＝fi＋ζbi，i∈［1，n］.wi，fi分别为含噪图像与原图像的小波系数，白噪声bi变换后在小波域中仍为白噪声bi.

对于小波模型wi＝fi＋ζbi，其Oracle投影子风险［13］为

式中，f为原图像小波系数；w为去噪后小波系数.

当采用硬阈值估计方法时，其风险为

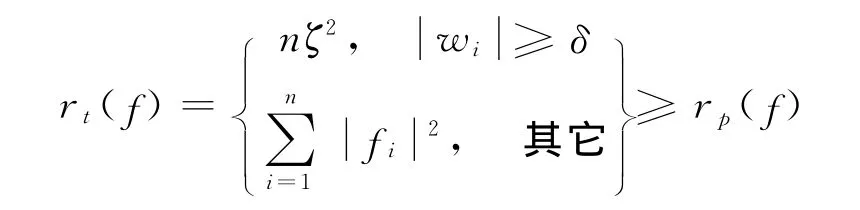
硬阈值估计的风险大于Oracle投影子的风险.对于软阈值估计，适当选取δ，其Oracle投影风险接近于Oracle投影子的风险.

对于改进的阈值函数估计的风险rn（f）：

当0＜wi＜δ时，

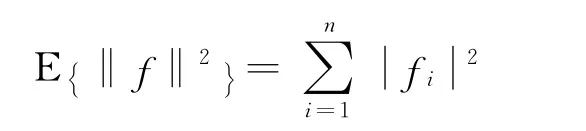
当－δ＜wi＜0时，

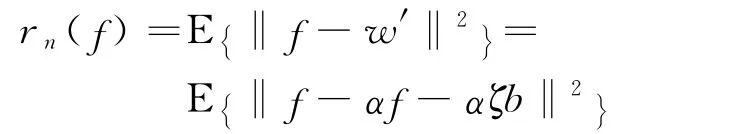
因此，改进的阈值函数估计的风险小于硬阈值函数的.虽然改进的阈值函数的小波系数幅值收缩程度比软阈值函数的小，其投影风险大于软阈值函数的，但通过调节参数α和δ的大小，可使其接近于软阈值函数估计的风险.

2.3 仿真实验

选取FVC2004指纹数据库中的102＿3.tif，103＿7.tif，104＿5.tif这3幅图像，分别利用软、硬阈值函数和改进的阈值函数进行仿真实验.采用Chang等［11］提出的自适应阈值（j＋1），其中，M，N为图像的尺寸，σ为标准差，j为当前分解层数.噪声图像经过小波分解后，噪声系数主要集中在高频部分，可以用分解尺度为1时的对角细节高频系数的标准差来估计噪声标准差.对图像加入标准差为18的高斯白噪声，采用db3小波作3层分解，α分别取0.1与0.2.实验结果如图2所示.只列举图像104＿5.tif的实验结果，“图2（e）”为α＝0.1时的去噪图像.

图2 不同阈值函数的去噪效果对比（α＝0.1和α＝0.2）Fig.2 The denoising effect comparison between various threshold functions（α＝0.1andα＝0.2）

由图2看出，经硬阈值函数和改进的阈值函数处理后的图像，比软阈值函数处理后的图像更加清晰，且细节特征更加明显.表1列出了采用不同阈值函数去噪后的峰值信噪比PSNR.当α＝0.1时，改进的阈值函数去噪法比软、硬阈值函数去噪法获得了更高的PSNR.当α＝0.2时，只有图像102＿3.tif的PSNR值略低于硬阈值函数的.因此，通过适当地选取α值，改进的阈值函数可以获得比传统的阈值函数更好的去噪效果.

表1 3种阈值去噪方法的PSNR比较Tab.1 Comparison of PSNR between three kinds of denoising methods dB

3 自适应模型的建立与检验

3.1 最优参数α的自适应选取

由以上实验可知，控制参数α的取值决定了去噪效果的好坏.现通过实验进一步研究α对去噪效果的影响.

对图像102＿3.tif分别加入标准差为18，21，24，27，30，33的高斯白噪声，利用改进的阈值函数进行去噪.在区间［0，1］内，利用二分法逐层确定α的最优值.规定：当二分次数s＝8或PSNR之差ε＜10－4时，终止二分，获得α最优值.计算结果如表2所示，保留两位有效数字.j代表分解层数.

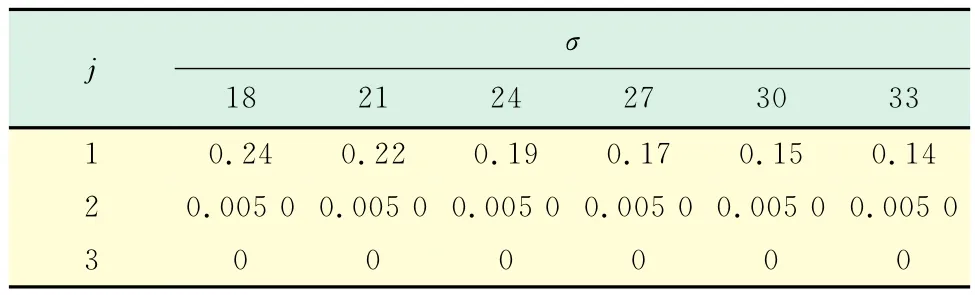
表2 不同噪声强度和分解层数下的控制参数α最优值Tab.2 The bestαunder different noise intensity and different decomposition layers

分析表2的数据可知，参数α在小波分解的第一层取值对去噪结果有着相对较大的影响.随着噪声强度的增大和分解层数的增加，α的取值呈变小趋势.当j＝1时，噪声的大小与α的取值呈负相关关系，采用多项式拟合将更符合模型的走势.对表2数据分别进行1～5次多项式拟合，对比模型的复相关系数（R－square）和误差平方和（SSE），在α的取值范围内，结合模型图像，本文选取经3次多项式拟合得出的σ－α模型，该模型复相关系数达到0.998 3，误差平方和为1.349×10－5.当j＝2时，α＝0.005 0；当j≥3时，α＝0.得到参数α关于噪声强度和分解层数的σ－j－α模型为

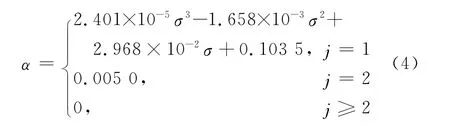
图3 不同α取值方法的去噪效果对比Fig.3 The denoising effect comparison between processing methods with different values ofα

当σ足够大，使得α＜0时，取α＝0.

3.2 模型验证

分别选取软、硬阈值函数、模型（1）的α值和最优α值对分别加入标准差为14，25，36的高斯白噪声的指纹图像103＿7.tif进行去噪.其中，噪声标准差为25的噪声图像的去噪效果如图3所示.

不同去噪方法的均方根误差峰值信噪比如表3所示.

其中，均方根误差

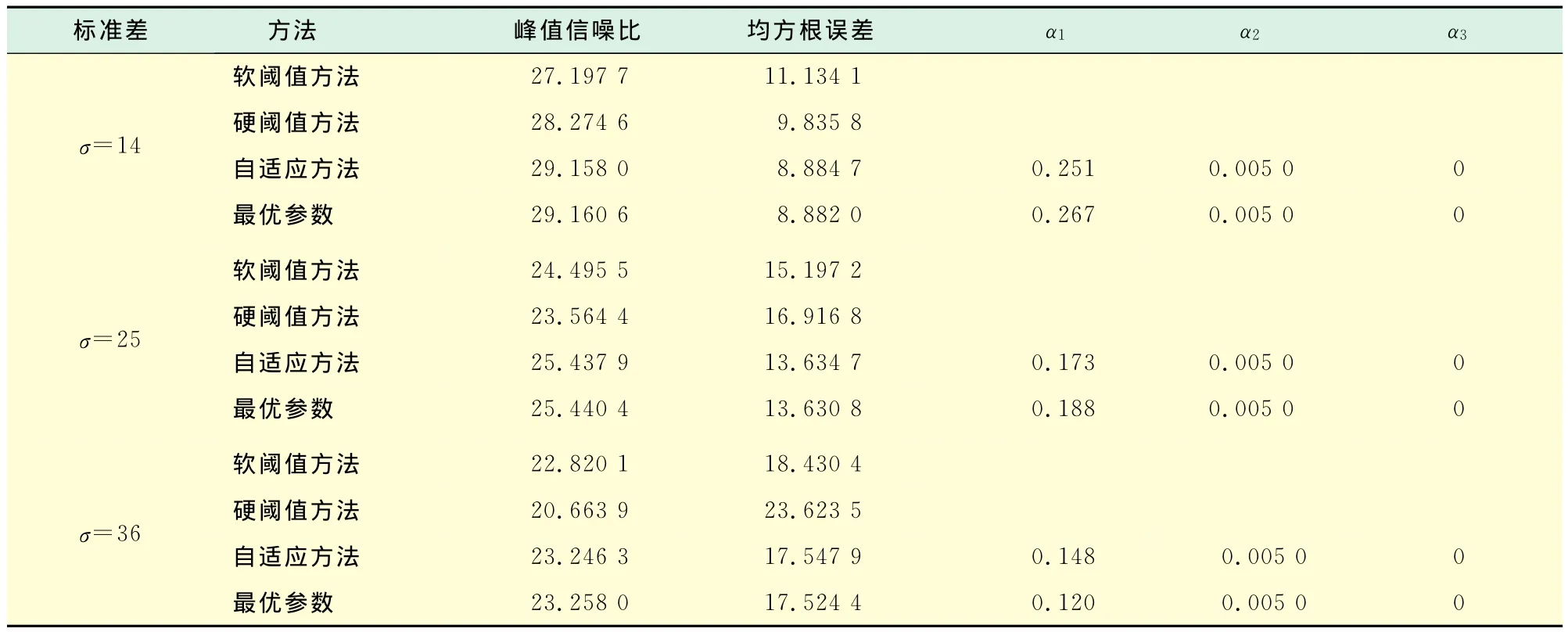
表3 不同α取值的峰值信噪比对比Tab.3 Comparison of PSNR with different values ofα

αj代表j层参数α的取值，j＝1，2，3.3个噪声图像的峰值信噪比分别为25.186 4，19.809 5，16.982 9dB.

由图3和表3可以看出，自适应模型和最优参数去噪效果接近，与软、硬阈值去噪相比，在更彻底去除噪声的同时，也保留了更多的图像细节信息，获得了更高的峰值信噪比和更小的均方根误差.由自适应模型得出的α值与最优值去噪后图像的PSNR值相对误差在1%以内.当σ分别为14，25，36时，其PSNR相比软、硬阈值法分别提高了3.5%～7.9%，4.2%～9.5%，4.5%～15.3%.

4 结 论

指纹图像去噪是指纹识别系统中的一个重要环节，对于指纹图像的读取、特征提取等具有重要的意义.本文针对传统的软、硬阈值去噪法在指纹图像去噪中的不足，提出了一种自适应选取参数的阈值函数，在一定程度上弥补了软、硬阈值函数的缺陷.仿真实验表明，该方法在有效去除噪声的同时，保留了指纹图像中重要的细节特征，与软、硬阈值法相比，去噪后的指纹图像有更好的视觉效果和客观评价.

［1］ 朱希安，曹林.小波分析及其在数字图像处理中的应用［M］.北京：电子工业出版社，2012.

［2］ Malfait M，Roose D.Wavelet－based image denoising using a Markov random field a priori model［J］.IEEE Transactions on Image Processing，1997，6（4）：549－565.

［3］ Nikpour M，Hassanpour H.Using diffusion equations for improving performance of wavelet－based image denoising techniques［J］.IET Image Processing，2010，4（6）：452－462.

［4］ Kazubek M.Wavelet domain image de－noising by thresholding and Wiener filtering［J］.IEEE Transactions on Signal Processing，2003，10（11）：324－326.

［5］ Kim C S，Kang T J.Automated defect detection system using wavelet packet frame and Gaussian mixture model［J］.Optical Society of America，2006，23（11）：2690－2701.

［6］ Mark M，Nick K.Image denoising using derotated complex wavelet coefficients［J］.IEEE Transactions on Image Processing，2008，17（9）：1500－1511.

［7］ Donoho D L.De－noising by soft－thresholding［J］.IEEE Transactions on Information Theory，1995，41（3）：613－627.

［8］ Donoho D L，Johnstone I M.Ideal spatial adaptation by wavelet shrinkage［J］.Biometrika，1994，81（3）：425－455.

［9］ Donoho D L，Johnstone I M.Adapting to unknown smoothness via wavelet shrinkage［J］.Journal of the American Statistical Association，1995，90（432）：1200－1224.

［10］ 王彦青，魏连鑫.一种改进的小波阈值去噪方法［J］.上海理工大学学报，2011，33（4）：405－408.

［11］ Chang S G，Yu B，Vetterli M.Spatially a daptive wavelet thresholding with context modeling for image denoising and compression［J］.IEEE Transactions on Image Processing，2000，9（9）：1522－1531.

［12］ Kaur L，Gupta S，Chauhan R C.Image denoising using wavelet thresholding［C］∥Proceedings of the Third Indian Conference on Computer Vision，Graphics ＆Image Processing.Ahmadabad：Allied Publishers Private Limited，2002，11：1522－1531.

［13］ 马拉特.信号处理的小波导引［M］.北京：机械工业出版社，2003.