内置发热圆的方腔内双扩散混合对流数值模拟研究
肖瑞雪, 李贝贝, 徐洪涛, 杨 茉
(上海理工大学能源与动力工程学院,上海 200093)
在自然界和工程应用中,许多过程同时受到热扩散和质扩散共同作用,如喷雾和闪蒸过程、雾化液体燃料的燃烧、旋风蒸发和干燥过程、化工和食品加工中的脱水及晶体生长等[1-6],这些问题可归结为双扩散混合对流问题.国内外许多学者对双扩散混合对流的问题进行了模拟研究.陈文等[7]研究了室内双扩散混合对流输运过程,分析了送风强度、热源强度及污染源强度对室内空气流动、热量与污染物输运过程的影响,并给出合理的控制室内温度和污染源传播的途径.Teamah等[8]对顶盖驱动的矩形腔内双扩散混合对流进行了研究,分析了顶盖向左右两个方向移动的情况,得出了两种移动情况下随着理查德数Ri的减小,传热和传质都减弱等结论.Al-Amiri等[9]对顶盖驱动腔体内双扩散过程进行了研究,指出低Ri时,顶盖驱动作用使得腔体内的传热和传质效应增强.Basak等[10]研究了底部均匀和不均匀加热两种情况下方腔内的混合对流情况,分析了不同雷诺数Re、普朗特数Pr以及格拉晓夫数Gr的影响,并对努赛尔数Nu的变化情况进行了分析.Nayak等[11]对顶盖驱动的立方腔内双扩散混合对流进行了研究,顶盖以恒定速度移动,并且温度和浓度梯度在腔体外部,分析了二维和三维情况下热壁面平均努赛尔数Nuav与平均舍伍德数Shav随着Re的变化情况.Kandaswamy等[12]分析了密度最大值对变壁温多孔介质腔内双扩散自然对流的影响.Sivasankaran等[13]研究了多孔腔内不定常密度流体的双扩散自然对流,给出了速度矢量图、等温线图、流线图以及等浓度线分布图,并分析了Nuav及Shav的变化情况.Nishimura等[14]研究了壁面具有水平温度和浓度梯度的矩形腔内振荡双扩散自然对流,讨论了浮升力比对双扩散对流的影响以及模型的震荡性问题.Chamkha等[15]对壁面具有相反的温度和浓度梯度的矩形腔体内磁流体双扩散自然对流进行了研究.Ching等[16]采用有限元法模拟分析了在Le一定时,Br,Ri以及移动壁的方向对正三角腔内传热和传质的影响.Chamkha等[17]研究了充满均匀多孔介质的倾斜长方形腔体内双扩散不稳定层流,对腔体内振荡流动进行了预测并且观察到了衰减振荡.Sun等[18]建立了一个微可压缩流模型研究封闭腔体内二元混合理想气体的双扩散对流,分析了变密度对充满二元混合理想气体的垂直腔内自然对流的影响.Hasanuzzama等[19]研究了Le对三角形腔体内传热和传质的影响.
从上述文献综述可知,目前大部分研究集中于顶盖驱动或侧壁移动情况下的双扩散混合对流,较少研究内部放置加热圆的方腔内双扩散混合对流问题,然而这是一个典型的污染物处理、热舒适性研究以及烟气控制等的简化模型.因此,本文对内部放置加热圆的方腔内二元双扩散混合对流现象进行了数值模拟研究,分析了Ri,Le,Br对方腔内双扩散混合对流的影响,给出了不同情况下的等温度线、等浓度线以及流线图,并分析了加热圆表面的Nuav和Shav的变化规律.
1 计算模型和方法
1.1 物理模型
如图1所示,方腔内置一加热圆,加热圆位于方腔中心.方腔的长宽均为L,圆的直径为d,其中d=0.4L.方腔设有开口,开口的大小为0.1L.流体从左侧底部流进,右侧顶部流出,进口速度为ui,温度为Ti,浓度为ci,圆表面的温度为Th,浓度为ch,方腔其余壁面绝热且浓度梯度为零,重力加速度为g,其中Th>Ti,ch>ci.方腔内流体Pr=0.7.
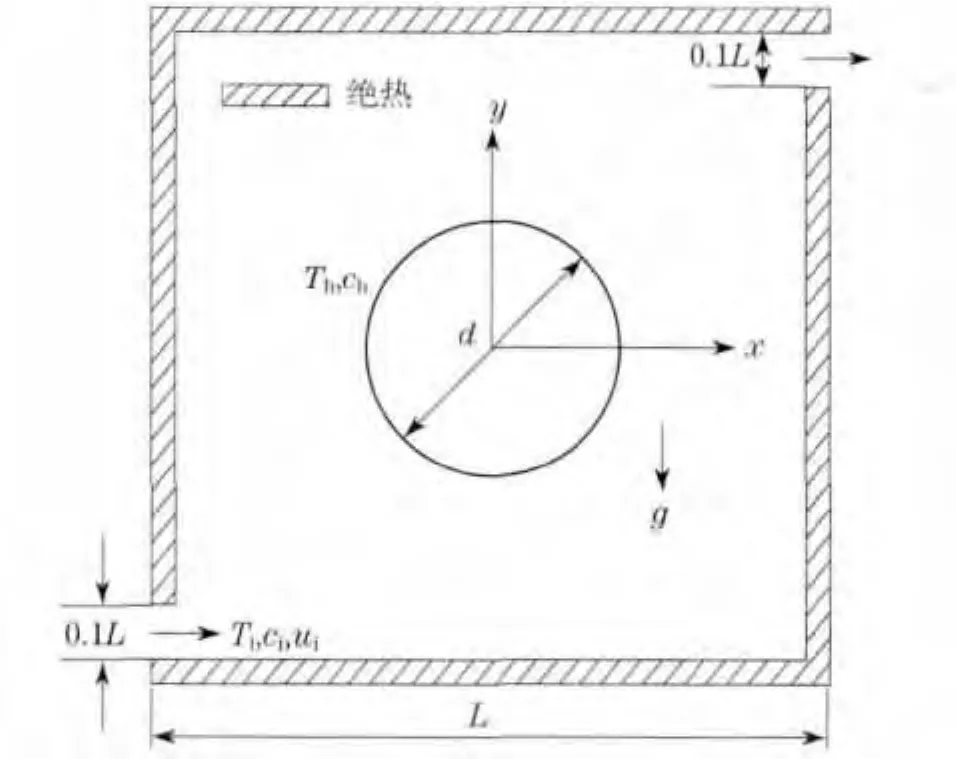
图1 物理模型Fig.1 Schematic diagram of thephysical model
1.2 数学描述
在进行方腔内对流换热和传质的数值计算时,为便于处理由于温差和浓度差而引起浮升力项,常采用Boussinesq假设[20]:

其中,ρ为密度;ρ0为与Τ0相对应的流体密度,kg/m3;βt为温度引起的体积膨胀系数为浓度引起的体积膨胀系数
定义下列无量纲参数

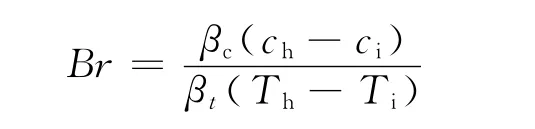
式中,u,v分别为直角坐标系下水平方向和竖直方向的速度分量;T,p,c分别为温度、压力和浓度;α,D,υ,g,为热扩散系数、质扩散系数、运动黏度、重力加速度.则图1所示的方腔内双扩散混合对流问题在直角坐标系下的无量纲数学描述方程为

无量纲边界设定为
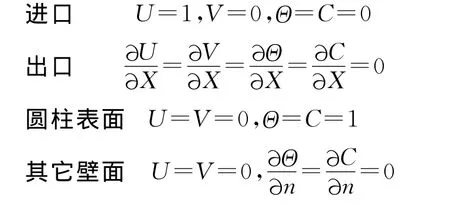
式中,n为表面法向.圆表面的局部Nu和局部Sh,可表示为

式中,h,hm为圆表面的局部换热系数和传质系数.圆表面的Nuav和Shav可表示为

1.3 计算方法
控制方程采用有限体积法[21]求解,方程采用二阶迎风格式离散.数值计算采用SIMPLE(semiimplicit method for pressure linked equations)算法进行压力速度耦合计算.为确保计算的准确性,进行了网格独立性验证,网格数分别取50×50,60×60,70×70,80×80,90×90和100×100,如图2所示.在网格数为100×100的情况下,数值解基本稳定.因此,最终选定网格数为100×100.数值计算时,连续性方程、动量方程和传质方程的计算残差取10-3,能量方程的计算残差取10-6.

图2 不同网格下的NuavFig.2 Grid independency check for the average Nusselt number around the heated cylinderat Ri=0.01,Br=10and Le=1
为了确保计算方法的准确性,本文对顶盖驱动的矩形腔内双扩散混合对流进行了研究,并将计算所得结果与文献[8]中的结果作了比较,如图3和图4所示.从图中可知目前的数值方法得出的结果与文献中的基本吻合,计算方法可行.

图3 等浓度线、流线和等温度线分布图(Pr=0.7,Ri=1,Br=1,Le=10)Fig.3 Isoconcentrations,streamlines and isotherms at Pr=0.7,Ri=1,Br=1and Le=10

图4 本文与文献[8]中Shav的比较Fig.4 Comparison of average Sherwood numbers
2 模拟结果分析
2.1 路易斯数Le的影响
Le是确定质量扩散和热扩散相对关系的重要参数之一,本文研究了Le在0.1与10范围内,方腔内的双扩散混合对流情况,图5给出了Ri=1及 Br=1时不同Le下等浓度线、流线和等温线分布情况.

图5 不同Le下等浓度线、流线以及等温线分布情况(Pr=0.7,Ri=1,Br=1)Fig.5 Effects of Lewis number on isoconcentrations,streamlines and isotherm at Pr=0.7,Ri=1 and Br=1
从图5可以看出流线和等温线的分布基本不随Le的变化而变化,而在发热圆表面的质边界层随着Le数的增加逐渐变薄,使得传质速率增加.Le=0.1时,等浓度线均匀分布在方腔左下角进口附近,方腔右上角浓度梯度几乎为零.随着Le的增大,等浓度线由进口逐渐向发热圆集中.当Le=10时,等浓度线大多集中在发热圆周围及出口附近,进口的浓度梯度几乎为零,加热圆上部的质羽流形状明显.从图5流线分布图可以看出,在进口附近有一个漩涡,流线部分从加热圆左侧绕过,部分从加热圆右侧流过,这是因为Ri=1时自然对流与强制对流作用相当.从图5等温线分布图可以看出等温线在发热圆和两侧壁之间分层分布,在发热圆左下角等温线分布较密集.

图6 不同Le下Nuav和Shav随Ri的变化情况Fig.6 Average Nusselt and Sherwood numbers
图6给出了Br=1时,不同Le下平均努赛尔数和平均舍伍德数随Ri的变化情况.从图6(a)可以看出同一Ri下,Nuav几乎不随Le的变化而变化.Nuav随着Ri的增加而逐渐减小,这是因为随着Ri的增加,强制对流作用减弱,从而减弱了整体换热效果.从图6(b)可以看出当Le≤1时,Shav随着Ri的增加而逐渐减小;当Le≥5,Shav随着Ri的增加先增加而后减小,因为低Le下Ri的影响占主导地位.从图6(b)还可以看出Shav随着Le的增加而增加,这是因为Le的增加使得传质效果增强.
2.2 浮升力比Br的影响
浮升力比Br也是影响方腔内双扩散混合对流的重要因素之一,不同的Br使得热边界层增厚或减薄.图7给出了Ri=1和Le=0.1时不同Br下等浓度线、流线和等温线分布图.Le=0.1表明质扩散比热扩散强.从图中可以看出,在Le=0.1时,等浓度线几乎不随Br的变化而变化,并且在进口附近均匀倾斜分层分布,图中可以观察到,数值为0.95的等浓度线随着Br的增大,逆时针偏转.Br=-10时,质浮升力占主导地位,且与热浮升力的方向相反.从图中可以看出,流线全部从发热圆左侧流过.随着Br的增加,大部分流线从发热圆左上角向右下角转移.当Br≥0时,流线在进口附近形成一个漩涡,并随着Br的增加逐渐增大,而等温线几乎不发生变化.

图7 不同Br下等浓度线、流线和等温线分布图(Pr=0.7,Ri=1,Le=0.1)Fig.7 Effects of buoyancy ratio on isoconcentrations,streamlines and isotherms at Pr=0.7,Ri=1 and Le=0.1
图8给出了强制对流Ri=0.01时,不同Le下平均努赛尔数Nuav和平均舍伍德数Shav随Br的变化情况.浮升力比的增大将增强自然对流作用,减弱强制对流作用.从图8(a)可以看出在Le=0.1时,Nuav不随Br的增大而变化,即浮升力比对低路易斯数的影响较小.其它情况下,Nuav随着Br的增大而逐渐减小.当Br从-10变化到10时,Nuav减小的速率随着Le的增大而增大.当Br=0时,从方程(4)可以看出,传质对流动没有影响,因而不同Le下Nuav相同.当Br>0时,Y方向的动量方程中源项增大,Le的增大增强了传质速率,平均努赛尔数Nuav随着Le的增大而减小.相反,当Br<0时,平均努赛尔数Nuav随着Le的增大而增大.同理,浮升力比的增大增强了自然对流作用,减弱了强制对流作用,从图8(b)可以很明显地看出,在0.1≤Le≤1时,Shav几乎不随Br的变化而变化,只是因为此范围内的质传递速率较大.当Le=5,10和15时,Shav受Br的影响较明显且随Br的增大而减小.同一Br下,Shav随着Le的增大而增大.

图8 不同Le下Nuav和Shav随Br的变化情况Fig.8 Average Nusselt and Sherwood number
为了更准确地了解加热圆不同位置处的传热传质情况,更好地反映Br对双扩散混合对流的影响.图9给出了在Le=1和Ri=1时,不同Br下发热圆表面局部Sh的变化情况.从图中可以看出,当Br≥0时,局部Sh的最大值在φ=240°处.当Br=-10时,Sh的最大值在90°<φ<120°之间.
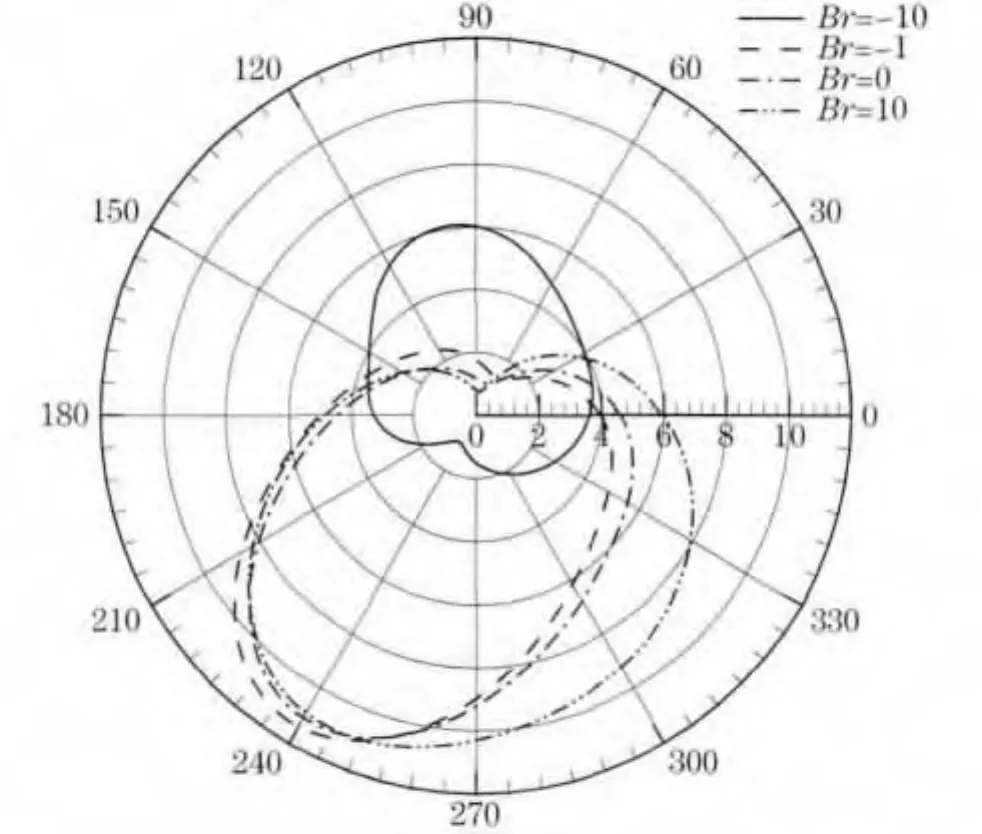
图9 发热圆表面局部Sh(Le=1,Ri=1)Fig.9 Local Sherwood number around the heated cylinder at Le=1and Ri=1
3 结 论
对内置发热圆的方腔内双扩散混合对流问题进行了数值模拟分析,得出以下结论:
a.当Ri=1和Br=1时,流线和等温线的分布基本不随Le的变化而变化,等浓度线随着Le的增大由进口逐渐向发热圆和出口集中.当Br=1时,Nuav几乎不随Le的变化而变化,随着Ri的增加而逐渐减小,Shav随着Le的增加而增加.当Br=1和Le≤1时,Shav随着Ri的增加而逐渐减小;当Br=1和Le≥5,Shav随着Ri的增加先增加而后减小.
b.当Ri=1和Le=0.1时,等浓度线几乎不随Br的变化而变化,并且在进口附近呈倾斜分层分布.随着Br的增加大部分流线从发热圆左上角向右下角转移.当Br≥0时,流线在进口附近形成一个漩涡,并随着Br的增加逐渐增大,而等温线几乎不发生变化.
c.当Ri=0.01时,Le=0.1时的Nuav几乎不随着Br的变化而变化,其它情况下Nuav随着Br的增大而逐渐减小,当Br从-10变化到10时,Nuav减小的速率随着Le的增大而增大.当Br>0时,Nuav随着Le的增大而减小,当Br<0时,Nuav随着Le的增大而增大.在0.1≤Le≤1时,Shav几乎不随Br的变化而变化,只是因为此范围内的质传递速率较大.当Le=5,10和15时,Shav受Br的影响较明显且随Br的增大而减小.同一Br下,Shav随着Le的增大而增大.
[1] Marcos J D,Izquierdo M,Parra D.Solar space heating and cooling for Spanish housing:potential energy savings and emissions reduction[J].Solar Energy,2011,85(11):2622-2641.
[2] Serrano-Arellano J,Xamán J,álvarez G.Optimum ventilation based on the ventilation effectiveness for temperature and CO2distribution in ventilated cavities[J].International Journal of Heat and Mass Transfer,2013,62:9-21.
[3] Ghaddar N,Ghali K,Chehaitly S.Assessing thermal comfort of active people in transitional spaces in presence of air movement[J].Energy and Buildings,2011,43(10):2832-2842.
[4] Vijaya Venkata Raman S,Iniyan S,Goic R.A review of solar drying technologies[J].Renewable and Sustainable Energy Reviews,2012,16(5):2652-2670.
[5] Yang M,Ma N.Free convection in a liquidencapsulated molten semiconductor in a vertical magnetic field[J].International Journal of Heat and Mass Transfer,2005,48(19/20):4010-4018.
[6] Hasan M,Mujumdar A S.Simultaneous mass and heat transfer undermixed convection along a vertical cone[J].International Journal of Energy Research,1985,9(2):129-140.
[7] 陈文,赵福云,汤广发,等.耦合墙体扩散的室内双扩散混合对流输运过程[J].暖通空调,2006,36(8):12-18.
[8] Teamah M A,El-Maghlany W M.Numerical simulation of double-diffusive mixed convective flow in rectangular enclosure with insulated moving lid[J].International Journal of Thermal Sciences,2010,49:1625-1638.
[9] Al-Amiri A M,Khanafer K M,Pop I.Numerical simulation of combined thermal and mass transport in a square lid-driven cavity[J].International Journal of Thermal Sciences,2007,46(7):662-671.
[10] Basak T,Roy S,Sharma P K,et al.Analysis of mixedconvection flows within a square cavitywithuniform and non-uniform heating of bottom wall[J].International Journal of Thermal Sciences,2009,48(5):891-912.
[11] Nayak A K,Bhattacharyya S.Double-diffusive convection in a cubical lid-driven cavitywith opposing temperature and concentration gradients[J].Theoretical and Computational Fluid Dynamics,2012,26(6):565-581.
[12] Kandaswamy P,Eswaramurthi M,Lee J.Density maximum effect on double-diffusive natural convection in a porous cavity with variable wall temperature[J].Transport in Porous Media,2008,73(2):195-210.
[13] Sivasankaran S,Kandaswamy P,Ng CO.Double diffusive convection of anomalous density fluidsin a porous cavity[J].Transport in Porous Media,2008,71(2):133-145.
[14] Nishimura T,Wakamatsu M,Morega A M.Oscillatory double-diffusive convection in arectangular enclosure with combined horizontaltemperature and concentration gradients[J].International Journal of Heat and Mass Transfer,1998,41(11):1601-1611.
[15] Chamkha A J,Al-Naser H.Hydromagnetic doublediffusive convection in arectangular enclosure with opposing temperature and concentration gradients[J].International Journal of Heat and Mass Transfer,2002,45(12):2465-2483.
[16] Ching Y C,Öztop H F,Rahman M M,et al.Finite element simulation of mixed convection heat and mass transfer in a right triangular enclosure[J].International Communications in Heat and MassTransfer,2012,39(5):689-696.
[17] Chamkha A J,Al-Naser H.Double-diffusive convection in an inclined porous enclosure with opposing temperature and concentration gradients[J].International Journal of Thermal Sciences,2001,40(3):227-244.
[18] Sun H,Lauriat G,Sun D L,et al.Transient doublediffusive convection in an enclosure with large density variations[J].International Journal of Heat and Mass Transfer,2010,53(4):615-625.
[19] Hasanuzzaman M,Rahman M M,Öztop H F,et al.Effects of Lewis number on heat and mass transfer in a triangular cavity[J].International Communications in Heat and Mass Transfer,2012,39(8):1213-1219.
[20] Gray D D,Giorgin A.The validity of the boussinesq approximation for liquids and gases[J].International Journal of Heat and Mass Transfer,1976,19(5):545-551.
[21] Patankar S V.Numerical heat transfer and fluid flow[M].New York:McGraw-Hill,1980.

