非有效市场中趋势驱动资产价格的波动估计
赵佃立
(上海理工大学理学院,上海 200093)
资产价格过程是金融市场中的一种复杂现象,其中,对资产价格过程的研究是很多学者的主要研究兴趣之一.在复杂的问题中,寻找简单而有效的模型来揭示规律,是一种有效的尝试.Fama于1970年提出了有效市场(EMH)的概念,认为证券的价格迅速地反映了所有信息,已经不可能从过去的价格趋势中获得未来盈利的机会.然而现实中依然存在许多该理论无法解释的现象,于是通过非有效市场的简单模型来揭示资产价格的规律成为有效的方法之一.Sornette,Johansen和Bouchaud[1]建立了资产价格的危机模型,并分析了危机前后资产价格的对数周期行为,随后Feigenbaum和Freund[2]通过数据验证了该模型的有效性.方勇和孙绍荣[3]研究了投资者情绪对证券投资的影响.张晓莉和严广乐[4]对沪深股票市场长程记忆相关性进行了研究.Appleby[5]提出了非有效市场资产价格的趋势驱动离散模型,并在确定和不确定情况下讨论了资产价格的极限行为.Markov过程是描述和研究资产价格模型的一个重要成分.Appleby与其合作者[6-8]对含有状态切换的金融模型进行研究,取得了一些重要的成果,并在文献[9]中对相关的方程进行了理论分析.本文基于文献[5]的工作,假设股价服从经典的Black-Scholes模型,将随机扰动项推广为含马氏驱动的随机过程,在给定的适当条件下得到价格的极限.在上述工作的基础上,考虑每个投资者的投资取向,建立含有马氏切换的非有效市场资产价格模型;通过考虑投资者价格取向的整体表现,推导出资产价格的波动边界.
1 模型描述
1.1 模型的建立
Appleby从投资者的角度建立和分析了一类离散趋势投机模型.假设资产累计收益
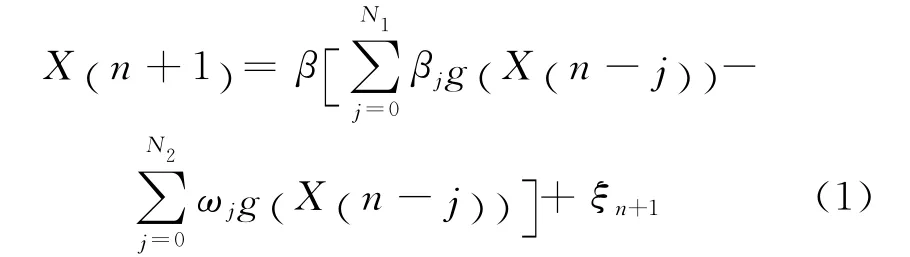
文献[5-6]讨论了上述模型的特例,并分析了资产价格过程在确定性和随机扰动两种情况下的极限行为.
本文在上述工作的基础上,建立趋势投机者驱动的马氏切换资产价格模型.记R(t)为累积平均收益率,定义X(t)=R(t)-μt,μ为固定收益增长率,则X(t)为资产收益超过固定增长的部分.如果市场存在趋势投机者,则会利用这一趋势进行投机行为.演化模型为
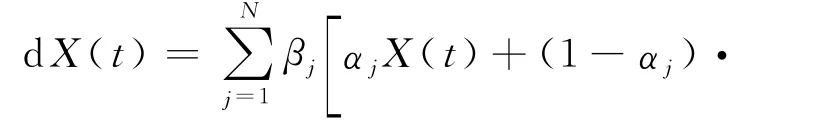
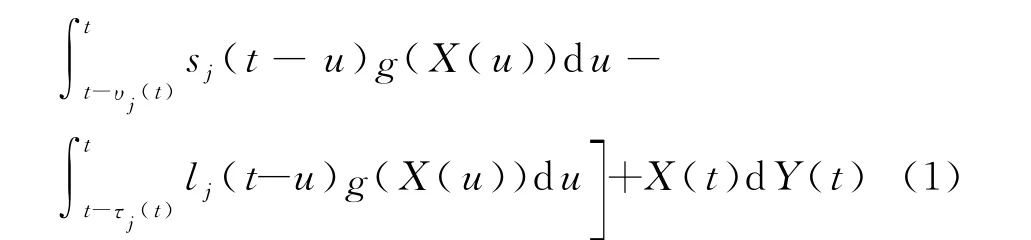
式中,υj(t)≤τj(t),j∈{1,2,3,…,N},表示记忆的长度;αj为正实数,反映了长期和短期之间的比重;N为正整数,表示投资者个数;sj和lj为加权函数;代表了第j个投资者选取的该资产的短期移动累积收益率;代表了第j个投资者选取的该资产的长期移动累积收益率;Y(t)是随机扰动项.
由于市场总是或多或少地受到一些不确定因素的影响,而且这些因素所在环境可能在不断变换,所以,假设Y(t)满足方程
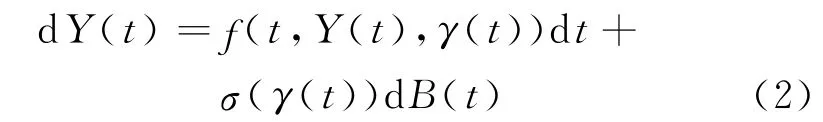
式中,γ(t)是有限状态空间S上的马氏过程;假设初值X(0)=x0>0;B(t)是服从标准正态分布的随机扰动项;扰动强度σ:S→R+,f(x,y,t)∈C(R×R× R+,R+).
主要利用随机分析知识和Volterra的理论对上述模型进行分析,内容包含了该模型的非线性项在有界性、幂函数、极限限制这3种情形下的波动估计.
1.2 基本概念与引理
假设B(t)是概率空间(Ω,F,(F(t))t≥0,P)的标准布朗运动,其中,域流F(t)=σ(B(s),γ(s):0≤s≤t).γ(t)是有限状态空间S={1,2,3,…,K}上的马氏链,Δt时间间隔上的生成算子Γ=(rij)N×N由
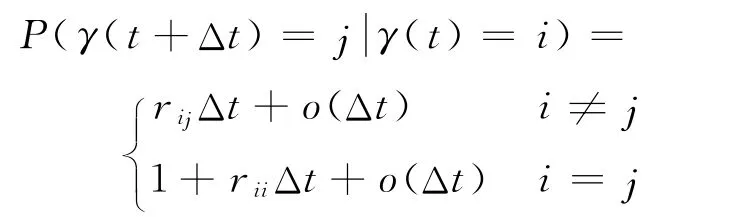
给出,rij≥0是从状态i到状态j的转移概率,满足.假设有唯一稳态分布π=(π1,π2,π3,…,πN).记Mi(n+1)=inf{t>Mi(n):γ(t)≠i}-Ti(n),Ti(n+1)=inf{t>Ti(n)+Mi(n+1):γ(t)=i},Li(n+1)=Ti(n+1)-Ti(n).那么,Li(n)对n=1,2,…独立同分布,均值为ri,方差为;Mi(n)对n=1,2,…也是独立同分布,均值为mi,方差为.
引理1[7]假设u,v:R+→R+,而且那么
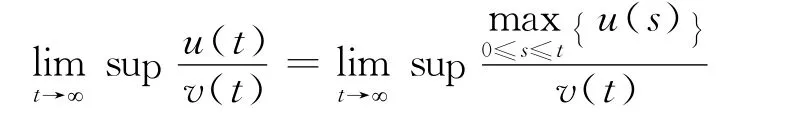
引理2[8]假设S是一个有限不可约状态空间,γ是一个平稳跳过程,而且σ:S→R,那么
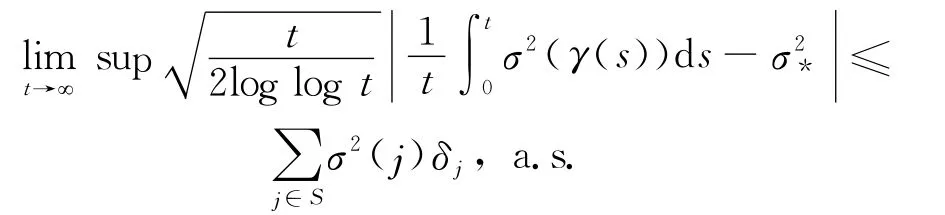
而且
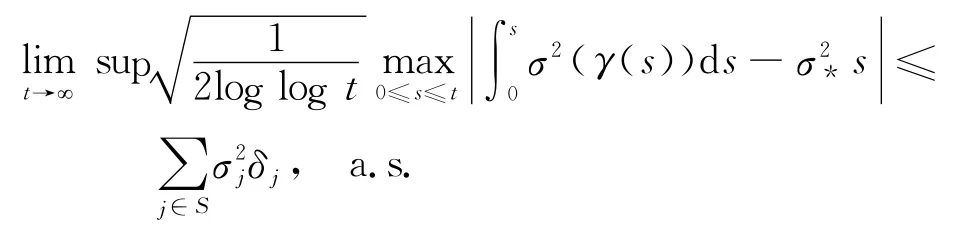
引理3[8]假设Y是式(2)的唯一连续适应解,初值Y(0)=Y0.如果存在常数c>0,使得对任意(x,y,t)∈R+×S×R+有
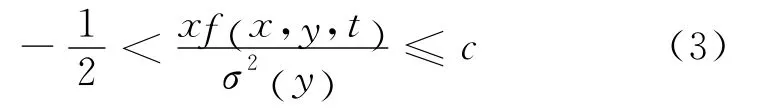
那么
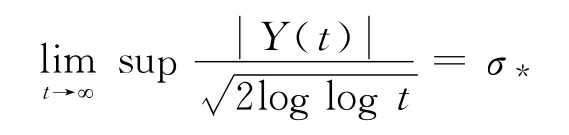
而且
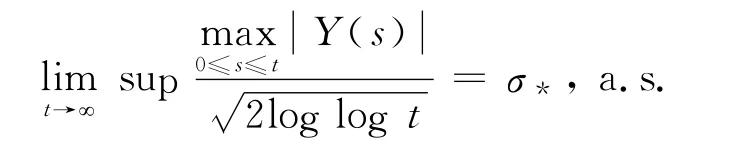
式中,σ*为标准差.
2 资产价格的波动估计
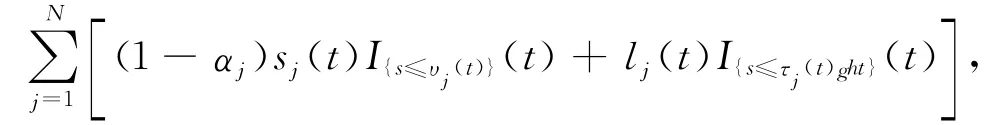
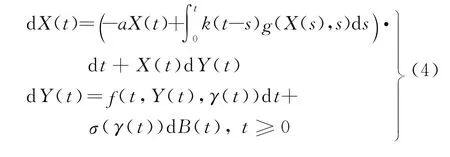
引理4和引理5给出了该模型解的表达式及其非负性质,其证明省略.
引理4 假设φ(t),y(t)满足方程
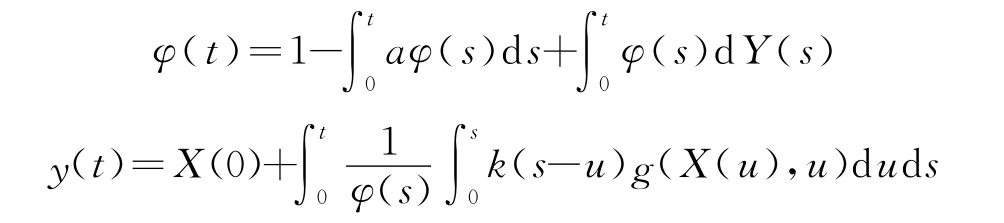
那么,方程(4)的解可以写成X(t)=φ(t)y(t).
引理5 假设函数g(·,·)和k(·)为非负连续函数,X是方程(4)的解,那么,X(0)>0(或X(0)≥0)可以依概率1推出X(t)>0(或X(t)≥0).
2.1 有界函数约束情形的波动估计
假设存在常数α1,α2>0,使得

定理1 假设X是方程(4)具有初值X(0)=x0>0的唯一连续适应解,a>0,k(t)>0是[0,∞)上的连续函数,且存在常数β∈(0,1)和正数b,c使得

如果式(3)和式(5)成立,那么
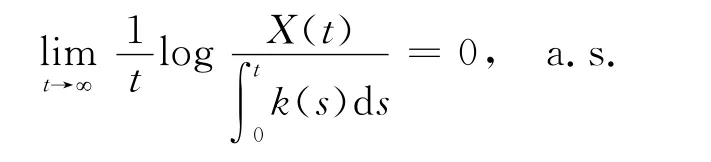
证明 对应αi(i=1,2)分别做辅助函数Zi满足
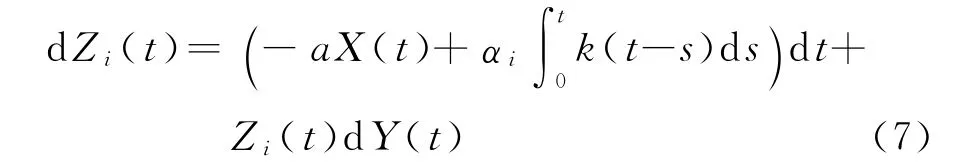
初值Zi(0)=X(0).由引理4知方程(7)的解为
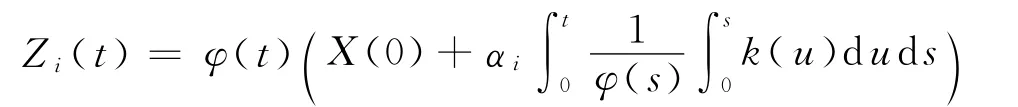
由k(t),φ(t)和X(0)的非负性及式(5)可得
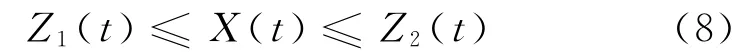
当i=2时,由式(8)得
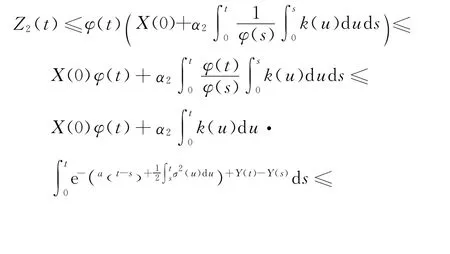
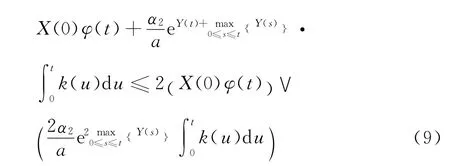
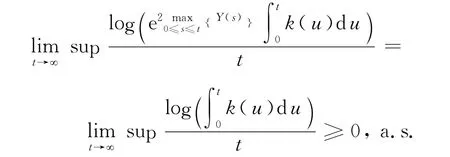
结合引理1和引理3推得
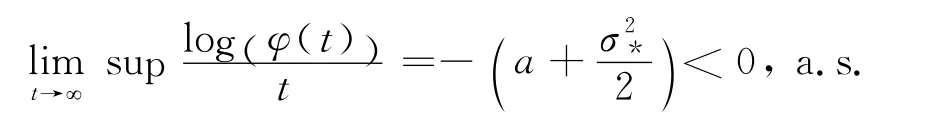
当t充分大时,由式(9)可得

两边取上极限,可得

现在证明反向不等式.由引理4推得
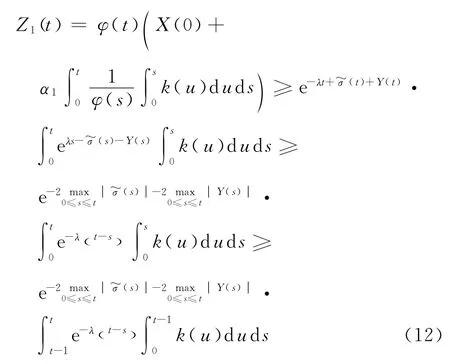
由引理2和引理3,在T1>0,使得当t>T1时,有和成立,于是,有
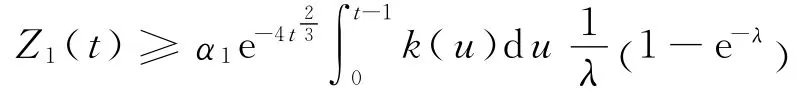
又由式(6)推得
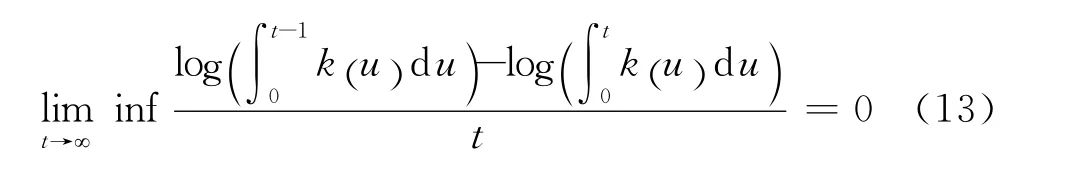
结合式(12)和式(13),有
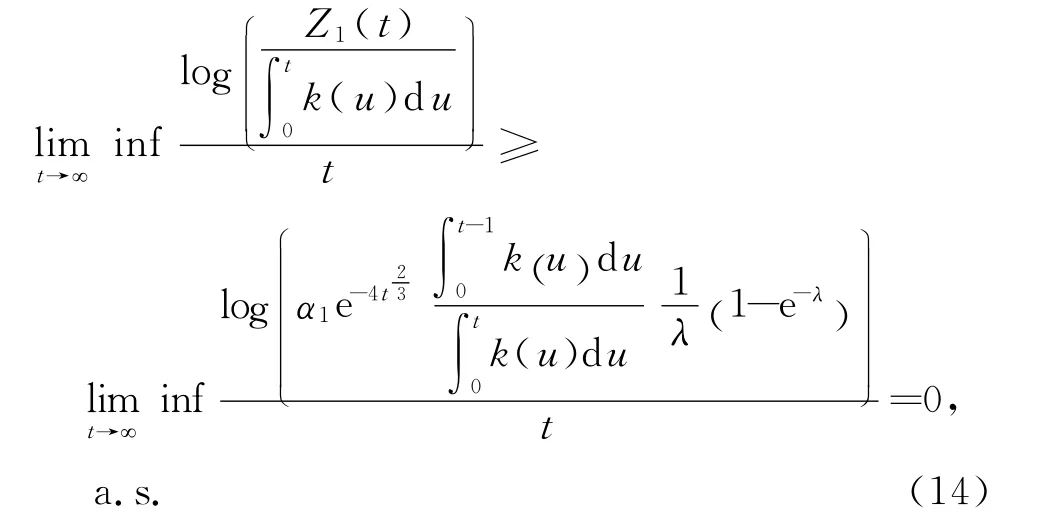
综上,由式(8)、式(11)和式(14)可得定理1成立.
推论1 假设X是方程(4)具有初值X(0)=x0>0的唯一连续适应解.k(t)>0是[0,∞)上的连续可积函数.如果式(3)和式(5)成立,那么
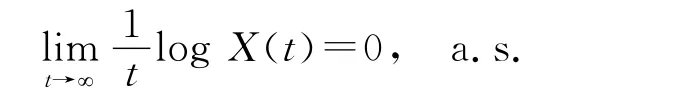
推论2 假设X是方程(4)具有初值X(0)=x0>0的唯一连续适应解,k(t)>0是[0,∞)上的连续函数,式(3)和式(5)成立.
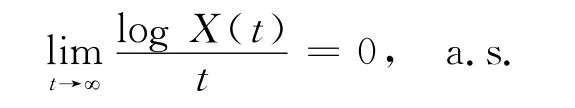
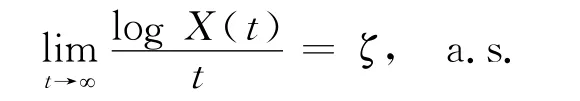
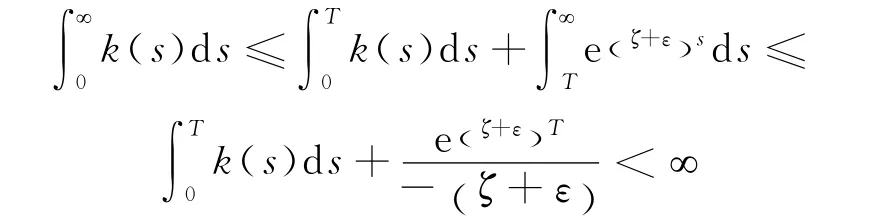
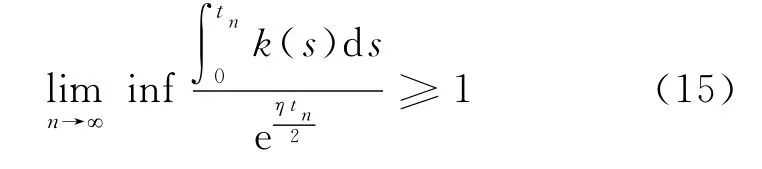
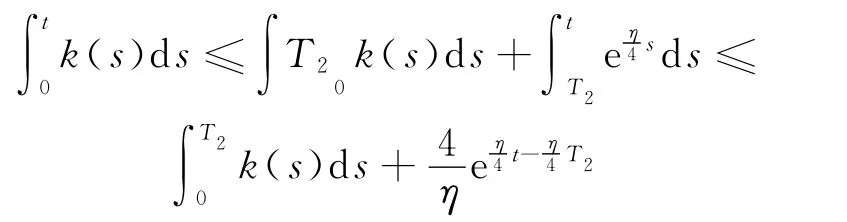
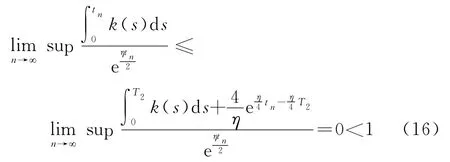
比较式(15)和式(16)可知,结论与
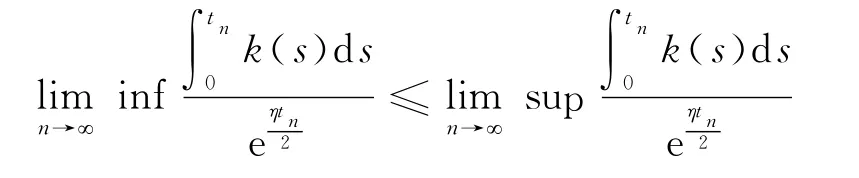
矛盾,所以,a得证.
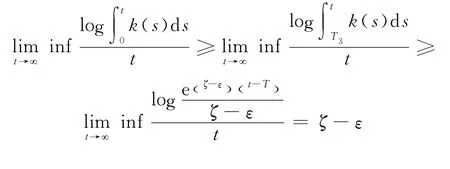
而且
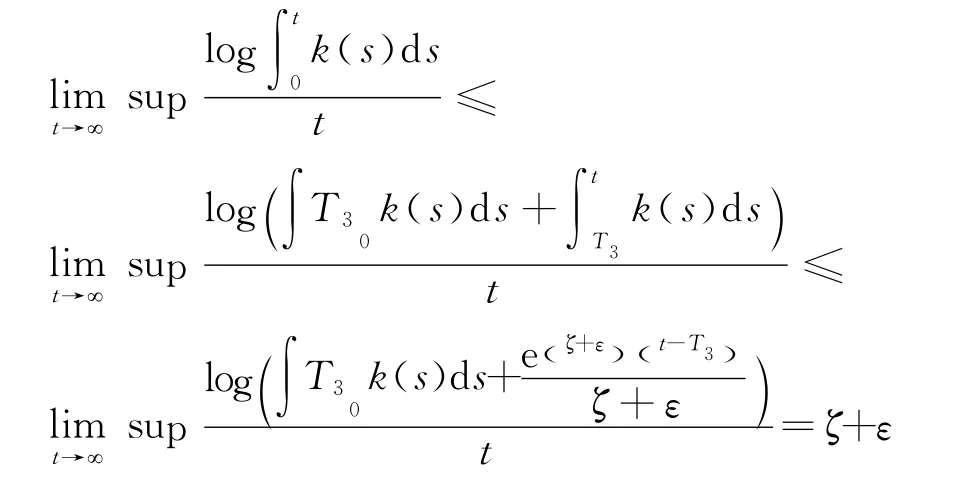
由上述结论可知,如果k(t)可积,那么,李雅谱诺夫指数为0,即非指数增长.定理2给出了更精确的增长边界估计.
定理2 假设X是方程(4)具有初值X(0)=x0>0的唯一连续适应解,k(t)>0是[0,∞)上的连续可积函数.如果式(3)和式(5)成立,那么,有
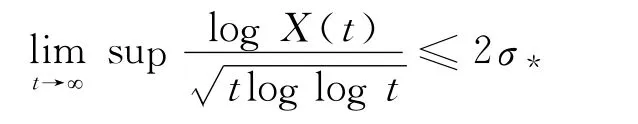
而且
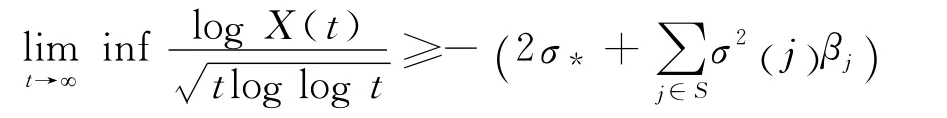
成立.
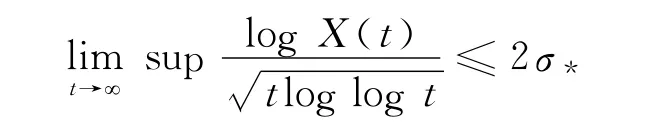
现证另一个不等式.当t充分大时,由式(12)
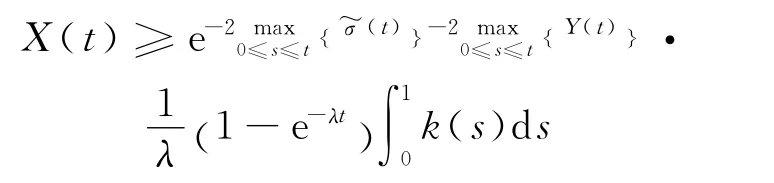

2.2 幂函数约束情形的波动估计
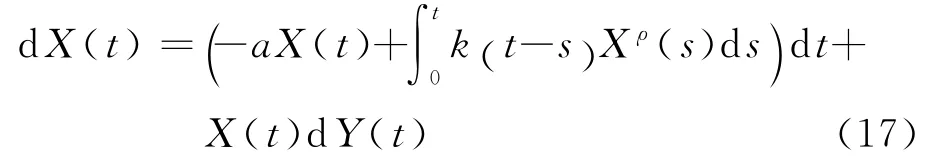
由引理4,将g x,(t)=xρ代入解的表达式,可得
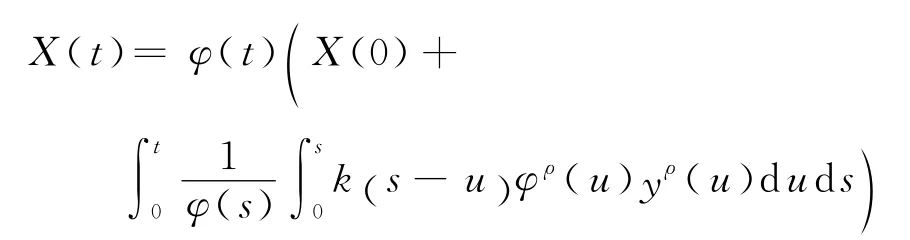
定理3 假设X是方程(4)具有初值X(0)=x0>0的唯一连续适应解,k(t)>0是[0,∞)上的连续函数,g (x,t)=xρ,ρ>0.如果式(3)成立,那么,有
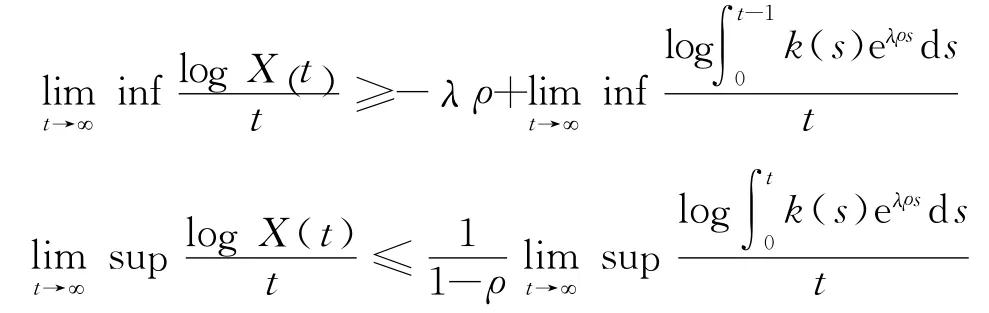
证明 由y(t)的定义可知,y(t)单调递增而且
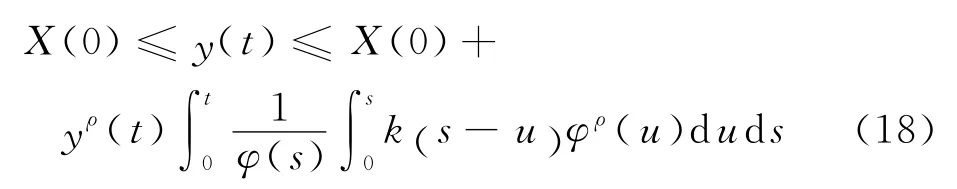
结合φ(t)的定义和式(18)推得
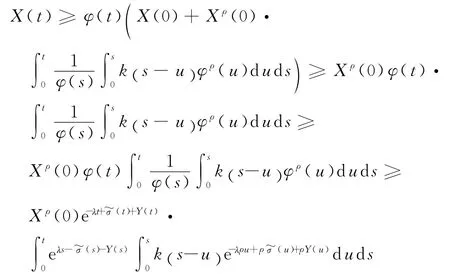
由引理2和引理3,当t充分大时,有
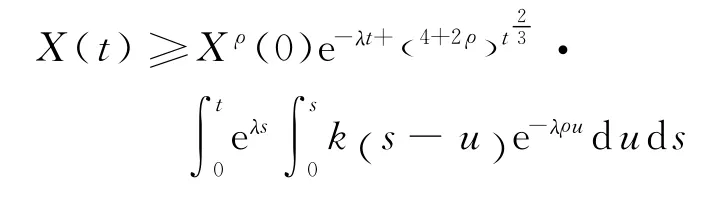
整理可得
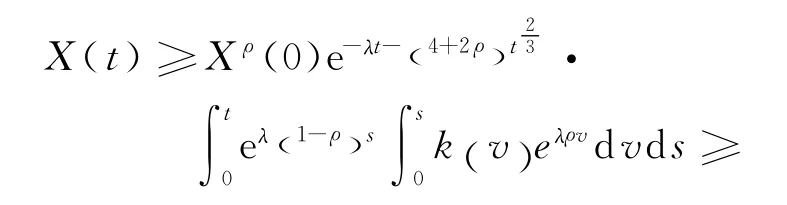
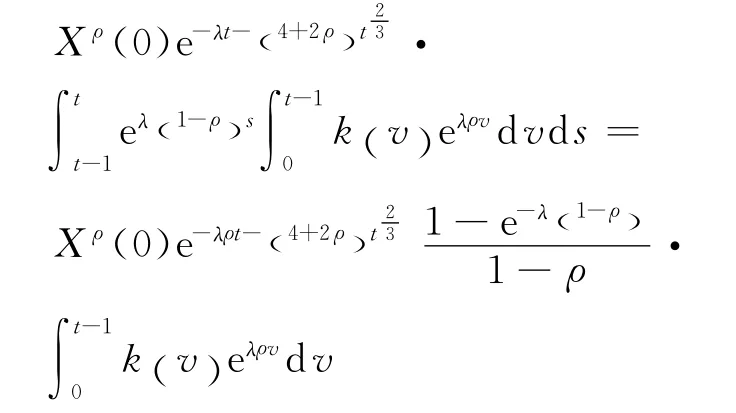
取下极限,推得
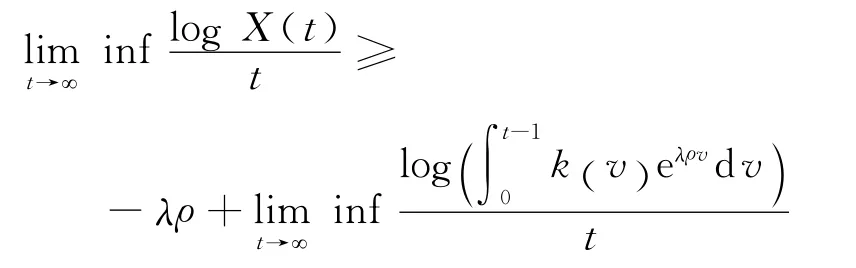
现证明关于上极限的不等式.结合引理2、引理3和式(18),推得
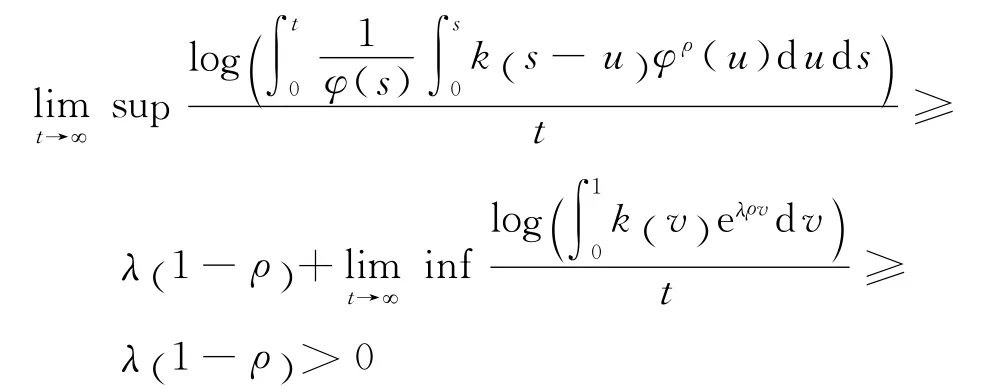
在式(18)两边取极限
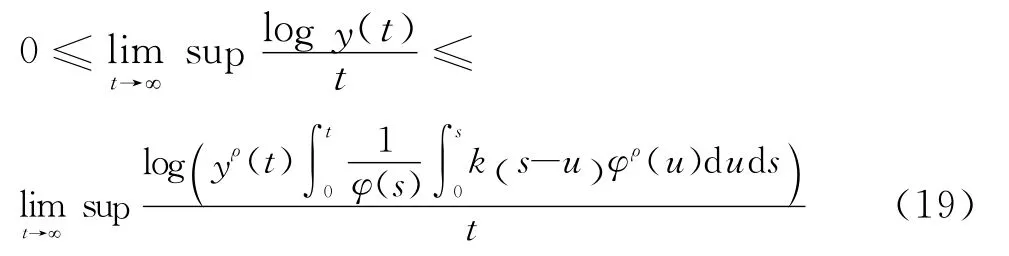
由于对任意t>0,有
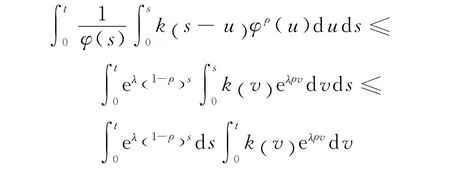
又由式(19)推得
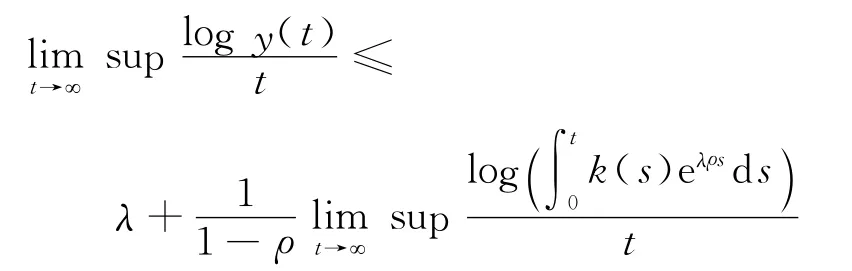
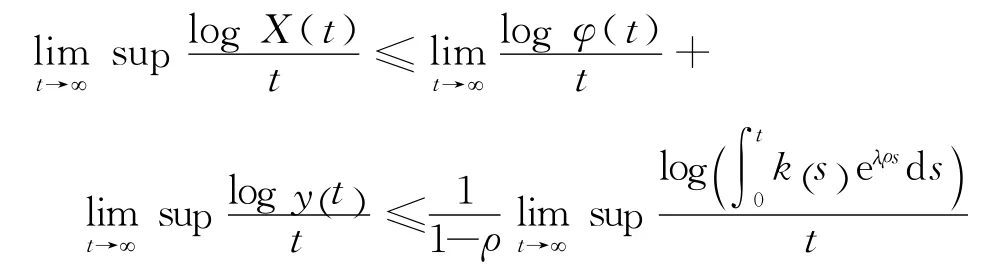
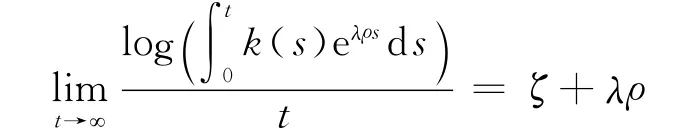
由定理3可知b成立.
2.3 极限限制情形的波动估计
假设存在正数β和ρ∈(0,1),使得
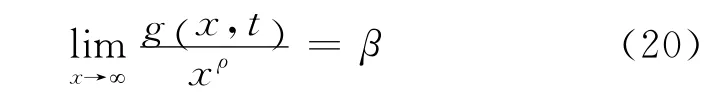
定理4 假设X是方程(4)具有初值X(0)=x0>0的唯一连续适应解,k(t)>0是[0,∞)上的连续函数,a>0,式(3)和式(20)成立,则有以下结论:
证明 先证明关于下极限的情形.由式(20),对任意ε∈(0,β),存在K=K(ε)>0,使得当x>K时,而且有又由方程的解非负可知,对任意t>0,存在L=L(ε)>0,使得g x,(t)<由引理4推得,X(t)=φ(t)y(t),而且
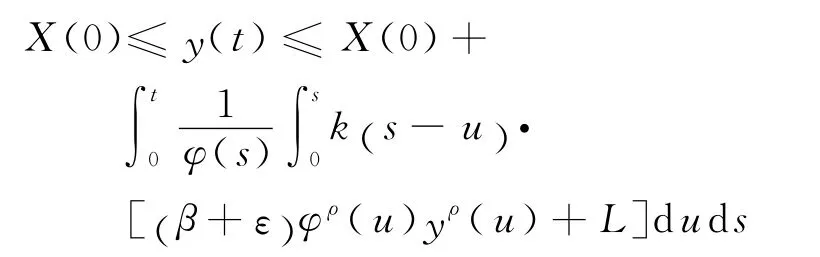
由定理3的证明易得

于是,由推论3可知以下关系成立:
现证明关于上极限的结论.由y(t)的单调性推得
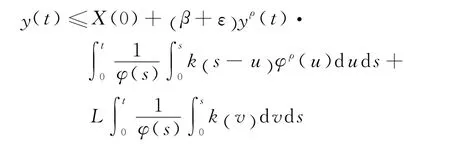
由引理2和引理3推得,当t充分大时,有
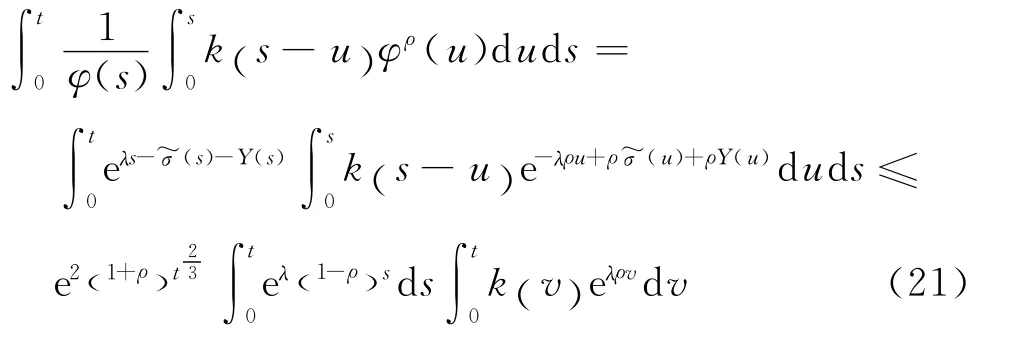
和
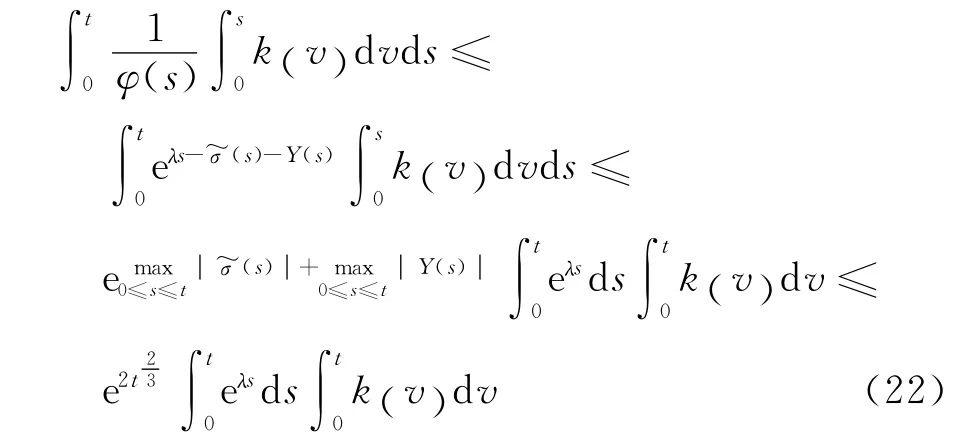
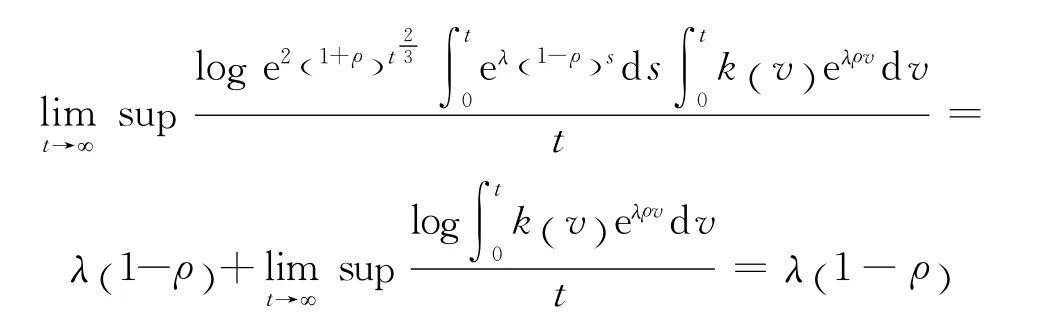
同时,由式(22)推得
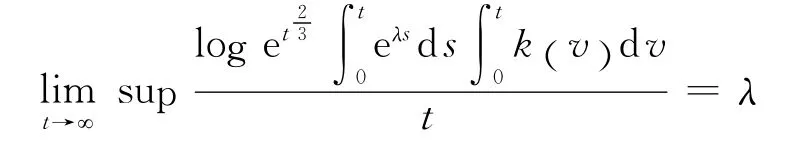
结合
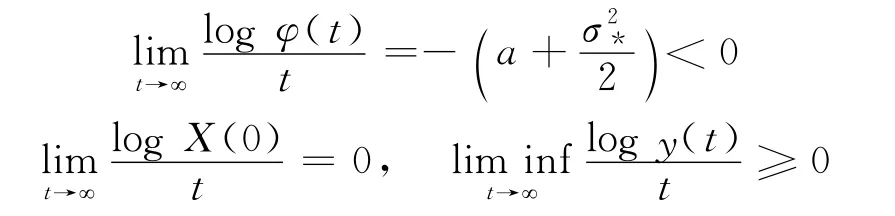
比较可得
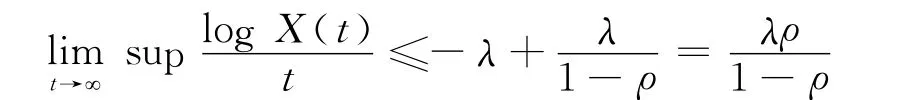
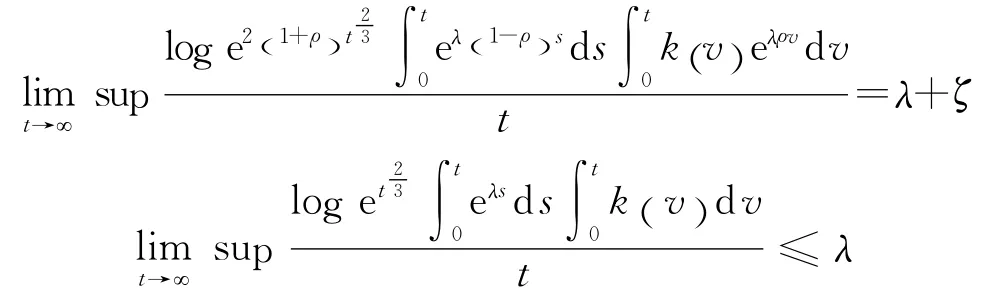
于是
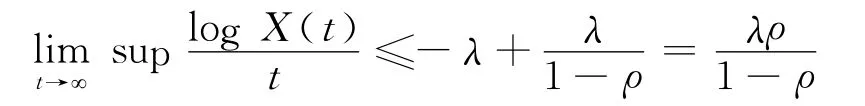

于是
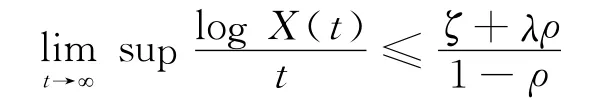
3 结 论
构造了具有马氏调制的非有效市场趋势驱动的资产价格模型.利用随机分析和Volterra方程的有关理论,对该模型在多种情况下的波动范围进行估计.在给定的条件下,资产价格的增长的边界估计依赖于反映投资者投资趋势的取向函数,马氏切换的引入打破了原有的价格增长边界.本文的理论结果推广了已有文献的有关结论.
[1] Sornette D,Johansen A,Bouchaud J.Stock market crashes,precursors and replicas[J].J Phys I(France),1996(6):167-175.
[2] Feigenbaum J A,Freund P.Discrete scale invariance in stock markets before crashes[J].Int J Modern Phys B,1996(10):3737-3745.
[3] 方勇,孙绍荣.影响证券投资者情绪的因素分析[J].上海理工大学学报,2008,30(2):157-161.
[4] 张晓莉,严广乐.沪深股票市场长程记忆相关性研究[J].上海理工大学学报,2006,28(3):237-241.
[5] Appleby J A D,Rodkina A,Swords C.Fat tails and bubbles in a discrete time model of an inefficient financial market[C]∥Proceedings of the 5th International Conference on Dynamic Systems and Applications.Atlanta:DYNAMIC PUBLISHERS INC,2007.
[6] Appleby J A D,Swords C.Asymptotic behaviour of a nonlinear stochastic difference equation modelling an inefficient financial market[J].Adv Stud Pure Math,2009(53):23-33.
[7] Appleby J A D,Wu H.Solutions of stochastic differential equations obeying the law of the iterated logarithm with applications to financial markets[J].Electron J Probabil,2009(14):912-959.
[8] Appleby J A D,Lynch T,Mao X,et al.The size of the largest fluctuations in a market model with Markovian switching[J].Communications in Applied Analysis,2009(13):135-166.
[9] Appleby J A D,Reynolds D W.On the non-exponential convergence of asymptotically stable solutions of linear scalar Volterra integro-differential equations[J].J Integral Equ Appl,2002,14(2):109-118.

